グラフ理論#0「グラフとは?」
はじめに
注意
調べたことをまとめる。
証明は適当なので使う時は自分で確かめてね。
初めての記事なのでおかしい所があれば指摘して欲しい。
この記事ではグラフといえば有限無向単純グラフを意味する。
今回の目標
グラフの基本的な用語に触れる。
こまごま定義0
有限集合の組$(V, E)$が以下を満たすとき、$(V, E)$はグラフであるという。
- $E \subset \{X \in 2^V \ |\ |X| = 2\}$
グラフ$G=(V,E)$に対し、$V$を$V(G)$, $E$を$E(G)$と書くことにする。
$V(G)$の元を頂点、$E(G)$の元を辺と呼ぶ。
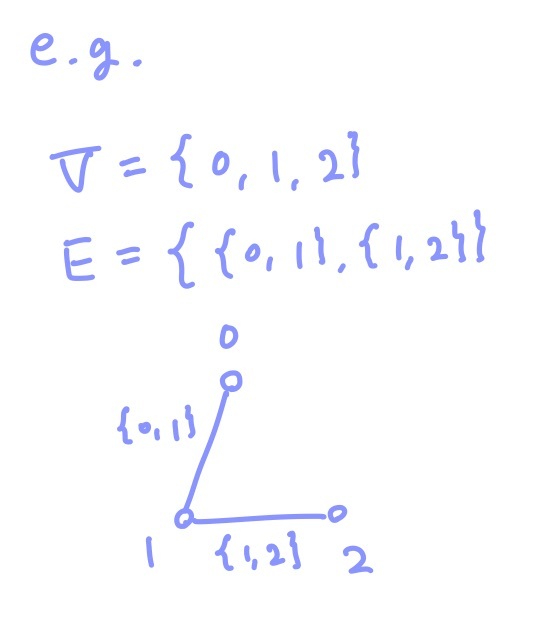 グラフの例
グラフの例
$G=(\varnothing,\varnothing)$を空グラフと呼ぶ。
$G$:グラフ
頂点$v \in V(G)$と辺$e \in E(G)$が接続している$:⇔ v \in e$
頂点$v_0, v_1 \in V(G)$が隣接している$:⇔ \{v_0,v_1\} \in E(G)$
辺$e_0, e_1 \in E(G)$が隣接している$:⇔ e_0\cap e_1 \not = \varnothing$
$G$:グラフ
$H=(V,E)$が$G$の部分グラフであるとは以下を満たすこと:
- $V \subset V(G)$
- $E \subset E(G)$
- $\forall e \in E, e \subset V$
$H$が$G$の部分グラフであることを$H \leq G$と書く。
部分グラフ$H \leq G$はグラフである。
$e \in E(H) \subset E(G)$だから$e$は$V(G)$の元の2点集合。
$e \subset V(H)$だから$e$は$V(H)$の元の2点集合。
$v \in V(G)$
$E_G(v):=\{e \in E(G)\ |\ v \in e\}$
$G$:グラフ
$V \subset V(G)$
$E \subset E(G)$
$H \leq G$
とする。
$$G \setminus E := (V(G),E(G) \setminus E)$$
$$G - V := (V(G) \setminus V, E(G) \setminus \bigcup_{v \in V}{E_G(v)})$$
$$H+E := (V(H) \cup \bigcup_{e \in E}{e}, E(H) \cup E)$$
$$G|_E:=(\bigcup_{e \in E}e,E)$$
これらはグラフ。
$G$:グラフ
$H \leq G$
$E \subset E(G)$
このとき
$(H \setminus E)+E \geq H$
さらに
$\forall e \in E, e \subset V(H)$
$E \subset E(H)$
ならば$(H \setminus E)+E = H$
$H \setminus E = (V(H), E(H) \setminus E)$
$(H \setminus E)+E = (V(H) \cup \bigcup_{e \in E}e, (E(H) \setminus E) \cup E)$
$(E(H) \setminus E) \cup E \supset E(H)$
$V(H) \cup \bigcup_{e \in E}e \supset V(H)$
だから、
$(H \setminus E)+E \geq H$
さらに
$\forall e \in E, e \subset V(H)$
$E \subset E(H)$
のときは
$(E(H) \setminus E) \cup E = E(H)$
$V(H) \cup \bigcup_{e \in E}e = V(H)$
だから、
$(H \setminus E)+E = H$
$G$:グラフ
$H \leq G$
$E \subset E(G)$
このとき
$\forall e \in E, e \subset V(H)$ならば
$(H+E)\setminus E \leq H$
$H+E = (V(H) \cup \bigcup_{e \in E}e, E(H) \cup E)$
$(H+E) \setminus E = (V(H) \cup \bigcup_{e \in E}e, (E(H) \cup E) \setminus E)$
$V(H) \cup \bigcup_{e \in E}e \supset V(H)$
$\forall e \in E, e \subset V(H)$だから$V(H) \cup \bigcup_{e \in E}e = V(H)$
$(E(H) \cup E) \setminus E \subset E(H)$
だから、
$(H+E) \setminus E = (V(H), (E(H) \cup E) \setminus E) \leq H$
$H_0,H_1$:グラフ
$H_0 \sqcup H_1:=(V(H_0) \sqcup V(H_1),E(H_0) \sqcup E(H_1))$
これは$H_0$と$H_1$を交わらないようにひとまとめにしたグラフ。
グラフ$G,G'$について$\phi:V(G)→V(G')$がグラフ準同型写像$:⇔ \forall \{v_0,v_1\} \in E(G), \phi(\{v_0,v_1\}) \in E(G')$
像の像を考えて$\phi(E(G)) \subset E(G')$とも書く。
互いに逆な準同型写像があるとき、$G,G'$は同型という。
これは頂点の隣接関係を保つ写像
全単射な準同型があっても必ずしも同型ではない。
基本となるベクトル空間
頂点空間
$G$:グラフ
$ \mathcal{V} (G):=2^{V(G)}$
$\mathcal{V}(G)$は$𝔽_2$代数になる。
$\mathcal{V}(G)$を$G$の頂点空間と呼ぶ。
$\mathcal{V}(G)$の元を頂点集合と呼ぶ。
頂点の1点集合全体は$\mathcal{V}(G)$の基底になる。
この基底を$\mathcal{V}(G)$の標準基底と呼ぶことにする。
$\dim(\mathcal{V}(G)) = |V(G)|$である。
辺空間
$G$:グラフ
$\mathcal{E}(G):=2^{E(G)}$
$\mathcal{E}(G)$は$𝔽_2$代数になる。
$\mathcal{E}(G)$を$G$の辺空間と呼ぶ。
$\mathcal{E}(G)$の元を辺集合と呼ぶ。
辺の1点集合全体は$\mathcal{E}(G)$の基底になる。
この基底を$\mathcal{E}(G)$の標準基底と呼ぶことにする。
$\dim(\mathcal{E}(G)) = |E(G)|$である。
グラフ同型
グラフ$G,G'$に対し、
$\mathcal{V}(G) \simeq \mathcal{V}(G')$かつ$\mathcal{E}(G) \simeq \mathcal{E}(G')$ならば$G \simeq G'$か?
そうでないとしても何か関係はあるか?