1種類の相性からなるゲームのナッシュ均衡
概要
パワーと相性からなるモデルを導入した対称二人零和ゲームについて、ナッシュ均衡を求める手続きを定めました。既存の等パワーのゲームの結果を拡張し、異なるパワーのキャラクターが含む場合も含めて計算しました。
また、均衡に含まれないような"弱い"キャラクターについても定量的な評価を行うことができます。
これらの結果は数値的な方法に頼らず閉じた数式の形で求めるため理論的な解析や定性的な考察を行いやすい形になっています。
はじめに
みなさん、こんちには。対戦前にキャラクター選択があるような種類のゲームの攻略法を考えたい!
わたしがやってるポケモン対戦では事前に育成した6匹しか使うことが出来ませんし、カードゲームでは事前に用意したデッキを持ち込む、格闘ゲームでは使用するキャラクターを試合前に選択するようなケースです。
じゃんけん的な相性概念がある場合も多く、自分の選んだキャラクターが不利な相手に当たって悲しい思いをした人も多いと思います。この手のゲームはそれなりにそのキャラクターで練習しておく必要があるため頻繁にキャラクターを変えるのも難しいことが多いです。
どうせ練習するなら「強い」キャラクターを選びたいですよね。
✊が✌️に有利なのがわかってもじゃんけんマスターになれるわけでは無いように、個々のキャラクター同士の相性がわかったからといってそれだけで即どのキャラ使えばいいかわかるわけではありません。
キャラクター同士の有利不利が完全にわかってる状態をスタート地点にして、複雑に絡み合う関係性のネットワークの中からどれを選ぶのが「強い」のか考えてみるというのが長期的なテーマです。
やること
- 特定条件のゲームでのナッシュ均衡の求め方
- "強い"キャラクターの探し方
やらないこと
- 具体的にどういうキャラクターが強いよ的な話
- 個別の証明
- ナッシュ均衡やパワーの高いキャラクターが本当に"強い"と言えるのか(別記事で出すつもりです)
扱う用語の定義
いくつかの用語を確認しておきます。
じゃんけんで互いのプレイヤーが✊✌✋が1/3ずつ出し合っているような状態をナッシュ均衡と呼びます。いつでもナッシュ均衡が最強!というにはそこまで単純ではないですが、ひとまず今回はナッシュ均衡(=じゃんけんでいうところの✊✌✋1/3ずつ)にあたる手を求めるのを目標にします。
縦に自分の使うキャラや戦略を並べ、横方向に相手を並べた表を作り、組み合わせごとに勝率を書き込みます この表から勝率部分だけ抜き出した行列を利得行列と呼びこの記事では基本的に文字Aを使って表現します。なお、相手と自分が対等な状態が50%=1/2とかいう中途半端な数字だと何かとキモいので全体から1/2引いておきます。
例えばじゃんけんは次のような関係を次のような利得行列で表現します。
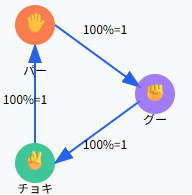 じゃんけんの三すくみ
じゃんけんの三すくみ
$$
勝率をそのまま書き込む→\pmatrix{
\frac12&1 &0 \\
0 &\frac12 & 1\\
1 & 0 & \frac12 \\
}
$$
$$
A=\pmatrix{
0 &\frac12 &-\frac12 \\
- \frac12 &0 & \frac12\\
\frac12 & - \frac12 & 0\\
}
$$
敵味方入れ替えて公平なゲームでは、$A_{12}=-A_{21}$ のようにナナメの部分でプラスマイナスが反転した数字が入ります(交代行列)。
利得行列の行列要素が大きくなればこちらの勝率が高い=有利であり、負の数になれば不利であることを表します。
相性が1種類
実は、現代科学においてはパソコンくんにお願いするとピピピピ…ピコーン!でナッシュ均衡がどうなるのかはわかります。 個々の勝率がわかっている状態をスタート地点にするなら計算方法自体は確立しているのです。ナッシュ均衡計算ライブラリ
じゃあわたし要らないじゃん! …となればよかったですが、PCくんに数字だけ教えてもらって理解出来てないと応用効かなくて困ります
そこで、難しい問題を理解するために理論屋さんがよくやる考え方として、実際の問題より理想的で簡単な状況を考えて、そちらについてめっちゃ詳しく解きます。
現実に近づけようとするといくらでも複雑な要素が付け加わりますが、理想的な状況が完全に解けていれば、それを基準にしてもっと増えるか減るかくらいは想像する事ができます。
利得行列Aはゲームの数だけ色んな種類がありますが、今回は計算や結果のイメージがやりやすく簡単で理想的な行列を仮定します。 具体的には次の形を今回扱う対象とします。
$$
A_{ij}=p_i-p_j+x_iy_j-y_ix_j
$$
上式のうち、pをパワー、2次元ベクトルv=(x,y)を相性と呼びます。本記事内の用語になります。
$A_{ij}$の相性部分は複数の表現ができます。次の表現はいずれも同じ意味です
$$ \begin{align} &x_iy_j-y_ix_j\\ &= v_i \times v_j & (ベクトルの外積) \\ &= ▲IOJ\mathrm{の面積の2倍} & \\ &= r_i r_j \sin(\theta_i-\theta_j) & (vの極座標表示) \end{align} $$
このように書くとき、パワーと相性の意味を確認しましょう。
$p_i$が増えると相手の戦略に関わらず利得行列は一定値増えます。つまり、相手が誰だろうが確実に勝率を担保できる潜在能力と言う意味でパワーです。
一方、相性部分は相手によって勝率が大きく変わり、自分の$v_i$と相手を表す$v_j$のベクトル同士の位置関係次第で大きく変化します。特に原点から見て90°ズレた方向の$v_j$手の時に大きくなります。vがどの方向を向いていれば最強というのがなく、ある方向を向いたvに強ければ逆方向のvに弱いといった相対的な関係を表すという意味で相性ベクトルと呼ぶことにします。
他の記事の主張
全ての証明を一つの記事に詰め込むと読み切れないですし、分割して色んな記事に飛び回るとそれはそれで読みにくいです。本記事で完結させるために、詳細な証明は分割してそれらの記事の結果のみこちらにまとめます。
等パワーゲームのナッシュ均衡 (結果①)
各キャラクターのパワーが全て等しく、利得行列が次のように書けるとき
$$
A_{ij}= r_i r_j \sin(\theta_i -\theta_j)
$$
適当な3キャラクターijkに対して次のような混合戦略sを定めるとsは均衡戦略になります。ただしC,C'はijkに依存しない共通項です。sは混合戦略なので確率的にキャラクターを選択しますが、lのキャラクターを選ぶ確率を$s_l$と書いています。
$$
\begin{align}
s_i&= C\frac{\sin(\theta_j- \theta_k)}{r_i}=C' A_{jk}\\
s_j&= C\frac{\sin(\theta_k- \theta_i)}{r_j}=C' A_{ki}\\
s_k&= C\frac{\sin(\theta_i - \theta_j)}{r_k}=C' A_{ij}\\
s_l&= 0 & l \neq i,j,k
\end{align}
$$
ただし、i,j,kは$v_i,v_j,v_k$が原点を囲むような3点である必要があります。
なお、どの3点も原点を囲まない場合(全部の点が右側半分にあるなど)は一番端の一点のみの戦略が均衡になります。
要するに全員等パワーのゲームでは任意の3キャラクターで3すくみが成立してそれが均衡になるということですね。
比の形で書くと共通項が消えてすっきりした形になります
$$ s_i:s_j:s_k=\frac{\sin(\theta_j- \theta_k)}{r_i}:\frac{\sin(\theta_k- \theta_i)}{r_j}:\frac{\sin(\theta_i- \theta_j)}{r_k} =A_{jk}:A_{ki}:A_{ij} $$
弱いキャラクターの定量評価(結果②)
キャラクターがどれだけ環境にあっていてその環境において"強い"キャラクタ―であるかを定量するために次のような指標を導入します。
均衡戦略がsの時、キャラクターiの環境乖離度$\kappa_i$を次で定義します。ただし、キャラクターiを100%の確率で使う純粋戦略を$e_i$とします。
$$
\kappa_i=- e_iAs = - \pmatrix{0&0&1(i列目)&0&0}A\pmatrix{s_1\\ s_2\\ s_3}
$$
このように定義したεが大きいほど環境から外れた「悪い」キャラクターであり、環境にあっていないことを表す指標になります。
これは直接的には相手が均衡戦略を選んでると考えて、それに対して最適化したキャラクターほど強いという考え方です。一見相手の戦略を仮定してそれに対してピンポイントメタ貼るようなナイーブな定義ですが、相手の戦略を戦略全体から探す場合でも上記の適合度が高い方が強い的な事が計算からわかります。
ゆるい均衡を使った構築評価 -最適でない構築の強さを定量化する-
ということで詳細は未来の記事に回しますが、今回は「環境乖離度εが小さいほど強い」を仮定して話を進めます。本当にこれが強いのか?は別記事になりますが、ここではどういう指標を乖離度として定義してどういうキャラクターほど強いことにして話を進めることにしているかが伝わればOKです。
低パワーキャラクターが加わった等パワー系(結果③-1)
等パワーで結果①で計算した3すくみの均衡が存在する時、それより低いパワーのキャラクターが加わっても等パワーの均衡戦略は低パワーキャラクター込みの環境でも均衡になります。
証明は次です( 記事が完成したらリンク張るスペース)
同じパワー同士でぎりぎり均衡になっているところにパワーの低いキャラクターが付け加わっても環境に影響を与えられないのは直観的にもイメージしやすいかと思います。
注意点として結果①の最後に触れたような、1キャラクターのみで均衡を作っているような場合は除外になります。3すくみの均衡作っている場合の結果です。
また、この時の環境乖離度(結果②で定義したやつ)は等パワー部分からのパワー差がそのまま環境乖離度になることが計算できます。
等パワーにするための平行移動ベクトル計算(結果③-2)
等パワーとは限らないp,vに対してaを定めます。i,j,kはp,vの中から任意に3点取ります。
$$
a= \frac{p_i(v_j-v_k)+p_j(v_k-v_i)+p_k(v_i-v_j)}T
$$
ただしTは$v_i,v_j,v_k$で作る三角形の面積の2倍であり、次で与えられます。
$$
\begin{align}
T&=(v_j - v_i)\times (v_k-v_i) & \mathrm{ \times は二次元の外積}\\
&=(v_k - v_j)\times (v_i-v_j)\\
&=(v_i - v_k)\times (v_j-v_k)\\
&=v_i\times v_j +v_j\times v_k +v_k\times v_i
\end{align}
$$
この時aを使った次のような変換により変換後の$p'_i, p'_j, p'_k$の3つは等パワーになります。
$$\begin{align}
p'_i &= p_i +v×a \\
v'_i &= v_i - a
\end{align}
$$
また、i,j,kが均衡になるためには単に等パワーである以外にも原点を囲む、i,j,k以外の点のパワーがi,j,kより低い等の条件がありますが、i,j,kの取り方を工夫することで良い感じにできます。
証明は次です( 記事が完成したらリンク張るスペース)
本題
それでは本題です。相性ベクトルの平行移動に関する基本的な性質を調べたのち、それと過去記事の結果を使ってナッシュ均衡を求めていきます。
相性の原点
さて、利得行列をパワーと相性を使って書いている時、実はパワーの数値は一つの値に決まっているものではなく、 ある法則にしたがう範囲で変更することが可能なのです。というのもあるp,vで利得行列Aを表現しているとき、同じ利得行列を表す別のp',v'があります。
本来、キャラクター同士の関係を表しているのは利得行列Aがあり、 パワーと相性はそれを理解しやすくするための補助線的なものにすぎませんから同じ利得行列になるような p,vがあるならそれらは等価であるとみなせます。
具体的には任意の二次元ベクトルaを用意して次のような変換を考えると変換後のp',v'が表す利得行列と元のp,vが表す利得行列がぴったり同じ値になります。
$$
\begin{align}
p'_i &= p_i + v_i\times a & \times は二次元の外積\\
v'_i &= v_i -a
\end{align}
$$
確認しましょう。
まず$A_{ij}=p_i-p_j +v'_i ×v'_j$のパワー部分からは$(v_i-v_j)\times a$が誤差として出てきます。
一方相性部分は次のようになります。
$$
\begin{align}
相性部分 &=v'_i\times v'_j \\
&=(v_i-a)\times (v_j - a)\\
&=v_i\times v_j -v_i\times a- a \times v_j+ a\times a \\
&=v_i\times v_j -(v_i-v_j)\times a + 0
\end{align}
$$
となり、こちらからも$(v_i-v_j) \times a$が出てきて符号が反対になります。したがって利得行列全体ではp',v'の利得行列もp,vの利得行列も同じ値になります。
$$
\begin{align}
A_{ij}=p'_i-p'_j +v'_i ×v'_j \\
=p_i-p_j +v_i ×v_j
\end{align}
$$
なお、この時v'=v-aはvの座標をaが原点になるように動かしたものとみなせます。相性の原点の取り方次第でパワーの数値も変動するわけです。
例えば次のような関係になっている時を考えます。
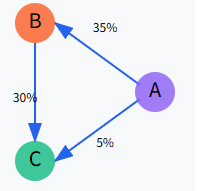 重み付き相関図
重み付き相関図
同様の状況
https://x.com/146Moltres/status/1458995967856984068
これは次のようにABCが均等な3すくみになっている+パワーによりCが不利になっていると考えることができます。
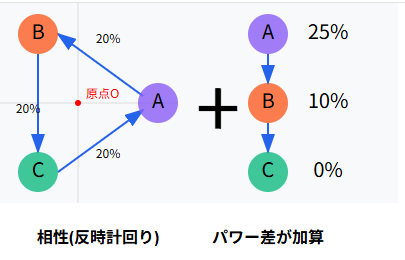 パワー+相性による相関図
パワー+相性による相関図
一方、次のように同じパワーで下のように原点Oを取っていると考えることもできます。原点からみて反時計回り方向に有利になるので原点が下のようになっていればABCが同じパワーでもA→Cになることを表現できるのです。
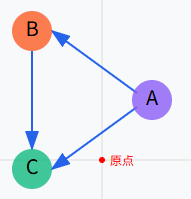 画像の名前
画像の名前
非等パワーゲームのナッシュ均衡計算
全部のキャラクターが同じパワーであれば過去記事で調べた通りで、結果①のようにナッシュ均衡がわかります。また、既にそのような均衡になっているゲームに対してそれより弱いキャラクターが追加されても、追加されたキャラクタ―がつかわれないだけなので同じ均衡になります(結果③-1)。
結果①の細かい条件も含めて整理すると以下の3条件を満たせば結果①の公式を使えます。
- 3キャラクター以上が等パワー
- 相性ベクトルの平面上で等パワーのキャラクターを結んだ3角形の内部に相性ベクトルの原点を含む(=等パワーキャラクターが3すくみになっている)
- 他キャラクターは等パワーのキャラよりパワーが低い
ここで相性部分の原点を変えればパワーを増減できたことを思い出します。いい感じに原点を選べば3キャラクターくらいであれば同じパワーにできそうです。実際に計算したものが結果③-2になります。
また、ナッシュ均衡に含まれないような"弱い"キャラクターの中で比較的ましなものがどれかといった問題は結果②の環境乖離度により評価できます。
以上をまとめると非等パワー環境のゲームの均衡戦略および均衡に含まれないキャラクタの環境乖離度を求める手順は次のようになります。
- $a=p_i\times (v_j-v_k)+ (いい感じにijk入れかえた項)$を計算
- 相性部分の原点をaに変更してキャラクターi,j,kを同じパワーにする
- 変更後の相性v'=v-aに対して$s_i=C \sin(\theta_j-\theta_k)/r_k$を計算してナッシュ均衡の時の強いキャラクターの比率を求める
- 変更後のパワー$p'=p+v\times a$を計算してナッシュ均衡に含まれないキャラクターの環境乖離度を求める。
- ナッシュ均衡と乖離度わかってハッピー。
具体例
最期に上記の手順を具体例で振り返っておきましょう。より実用的な例をすることも考えましたが、量の関係で手順の振り返りに目的を絞ります。この記事の反響次第で別記事として応用例専用の記事も出すかも。
あるカードゲームで5種類のデッキがあって、互いの勝率が次のようになっている環境になっていたとします。
| (勝率-50%)の表 | 赤アグロ | 青コントロール | 黒コンボ | 白ミッドレンジ | 緑ランプ |
|---|---|---|---|---|---|
| 赤アグロ | 0% | 24% | -8% | 2% | -25% |
| 青コントロール | -24% | 0% | 12% | -8% | 15% |
| 黒コンボ | 8% | -12% | 0% | 20% | 35% |
| 白ミッドレンジ | -2% | 8% | -20% | 0% | -25% |
| 緑ランプ | 25% | -15% | -35% | 25% | 0% |
これは各キャラクターが次のようなパワー、相性ベクトルを持っていると考えると上記の勝率を再現できます。
| キャラクター | パワー | 相性ベクトル |
|---|---|---|
| 赤アグロ | 62% | (20%,-30%) |
| 青コントロール | 38% | (-20%,30%) |
| 黒コンボ | 48% | (-40%,-50%) |
| 白ミッドレンジ | 53% | (10%,-50%) |
| 緑ランプ | 55% | (-20%,-130%) |
例えばアグロ vs コントロールの対戦はパワー差により24%、相性差により(20%,-30%)×(-20%,30%)=0%なので合わせて24%分だけアグロ側が有利です。アグロ vs コンボではパワー差14%、(20%,-30%)×(-40%,-50%)=-22%となるので合わせて-8%となりコンボ側微有利です。
このような計算を繰り返すことで、これらのパワーと相性ベクトルによる表記で勝率を表現できていることが確認できます。
これらのパワー、相性ベクトルの表し方は一通りではないので、同じパワーのキャラクタ―が出来るように相性ベクトルの原点を変更します。アグロ、コントロール、コンボを1,2,3だと思って結果③-2の計算式を使うと次のようになります。
$$
\begin{align*}
a&=62\% \times \left( \pmatrix{-20\% \\ 30\%}-\pmatrix{-40\% \\ -50\%} \right)\\
&+38\% \times \left( \pmatrix{-40\% \\ -50\%}-\pmatrix{20\% \\ -30\%} \right)\\
&+48\% \times \left( \pmatrix{20\% \\ -30\%}-\pmatrix{-20\% \\ 30\%} \right)\\
&/T\\
&=\pmatrix{14.4\% \\-14.4\%}
+\pmatrix{-22.8\% \\24.8\%}
+\pmatrix{19.2\% \\ -24.8\%}\\
&/T\\
&=\pmatrix{8.8\% \\ 13.3\%}/T
\end{align*}
$$
T部分の計算は次です。
$$
\begin{align}
T & = \pmatrix{-20\% \\ 30\%} \times \pmatrix{20\% \\ -30\%}
+ \pmatrix{20\% \\ -30\%} \times \pmatrix{-40\% \\ -50\%}
+ \pmatrix{-40\% \\ -50\%} \times \pmatrix{-20\% \\ 30\%}\\
& = -440\%
\end{align}
$$
合わせると次です。
$$
a=\pmatrix{-20\% \\ -30\%}
$$
実際、$p'=p+v\times a, v'=v-a$でこのaを原点にした時のパワーを求めると次のような表になります。
| キャラクター | パワー | 相性ベクトル |
|---|---|---|
| 赤アグロ | 50% | (40%,0%) |
| 青コントロール | 50% | (0%,60%) |
| 黒コンボ | 50% | (-20%,-20%) |
| 白ミッドレンジ | 40% | (30%,-20%) |
| 緑ランプ | 35% | (0%,-100%) |
①アグロ、コントロール、コンボの3つが同じパワーになり②その3つの間で三すくみが成立し③他のキャラクターはそれ以下のパワー、の3点が揃ったので等パワーのナッシュ均衡の公式(結果①)が使えます。ナッシュ均衡は以下です。
| キャラクター | 比率 |
|---|---|
| 赤アグロ | 27% |
| 青コントロール | 18% |
| 黒コンボ | 54% |
| 白ミッドレンジ | 0% |
| 緑ランプ | 0% |
実際、(27%,18%,54%,0%,0%)の相手とAの利得行列で対戦すると全部0%になって勝ち越せないことがわかると思います。
また、この時のパワーにより環境からの乖離度を定めることができます。0%のキャラクター同士ミッドレンジとランプとで比較することができ、ミッドレンジの方がより環境に合っていることが定量的にわかります。
| キャラクター | 乖離度 |
|---|---|
| 赤アグロ | 0% |
| 青コントロール | 0% |
| 黒コンボ | 0% |
| 白ミッドレンジ | 10% |
| 緑ランプ | 15% |
以上の手順でナッシュ均衡や環境乖離度を求めることができます。
終わりに
いかがでしたか?
パワーと相性のモデルで対戦ゲームをモデル化して、パワーが違うゲームについても均衡解を求めてみました。
いい感じに平行移動してパワーを揃えれば等パワーの結果を使えて低パワーキャラクターの使用率が0になる、ということで面白い結果になったんじゃないかと思います。
均衡解自体は数値計算でいくらでも求められますが、簡単なモデルであっても手計算の結果がわかっていると何かと応用が効いて便利です。
数値計算でだとパラメータ変えるたびにシミュレーションしなおさなきゃなので意外と面倒なんですよね。その点、今回みたいなやり方で$y=x^2+x+\dots$みたいに数式で書けると「あ、こいつはx増えると大きくなる量なんだな」っていうのが一目瞭然です。
例えばTCGで自由枠のカードを変更した時の影響やポケモンで持ち物を微調整した影響をパラメータの形で相性ベクトルの中に含めれば「この変更すれば二次関数で強くなるぞ!」や「あのパラメータが増えるような変更はむしろ弱くなるからやっちゃだめだな」的な考察に繋がります。
色んな考察できると思うのでいまからwktkです。
マジ個人的な感想になりますが、これまでにこのテーマで投稿した記事はモデルを作っただけだったり、パワーの定義がwell-definedになってなかったりの段階の投稿だったので、本投稿のための準備の側面が強かったので、今回閉じた形にまとめることが出来てようやく一段落という気分です。疲れた~~
次回以降は今回の記事で後回しにすると宣言した証明の部分だったり、今回の結果の有用性を示すための具体例やシミュレーションだったりを書いていくことになります。お楽しみに
ではでは~~~
