凸集合と凸結合

708

凸集合と凸結合

この記事では凸結合の定義と凸集合と関連する命題について扱います。

凸結合の定義

凸結合の定義と図による解釈を説明していきます。

$x_1, \cdots ,x_n$の$convex \ combination$（凸結合）
$\Leftrightarrow x= \lambda_1 x_1 + \cdots + \lambda_n x_n \ (\lambda_1, \cdots ,\lambda_n \geq 0, \sum_{i=1}^{n} \lambda_i =1)$
$(x= \sum_{i=1}^{n} \lambda_i x_i \ (\lambda_1, \cdots ,\lambda_n \geq 0, \sum_{i=1}^{n} \lambda_i =1))$

凸結合とは任意の点に対して、各係数の和が$1$となる正の係数でスカラー倍した点の和となります。このように書いても全くイメージがしにくいので、まず2つの点で考えてみることにします。

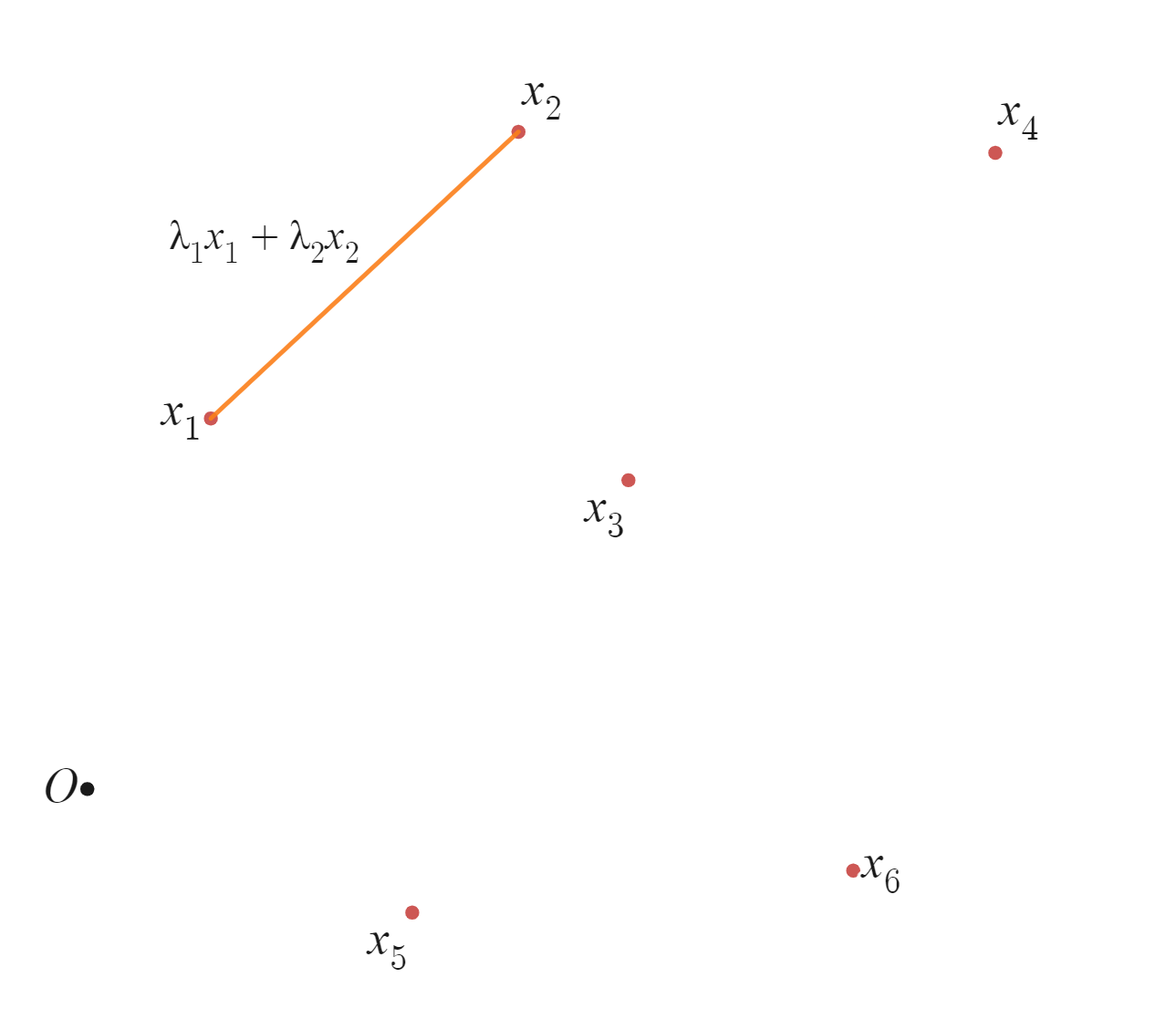凸結合（2点）

この図の点$x_1,x_2$で考えてみると、$\lambda_1,\lambda_2 \geq 0, \lambda_1 + \lambda_2 = 1$に対して、$\lambda_1 x_1 + \lambda_2 x_2$は橙色の線分となります。ここで$\lambda_2 = 1 - \lambda_1$であることに注目すると、2点の凸結合は$\lambda_1 x_1 + (1 - \lambda_1) x_2$となります。この式には見覚えがあると思いますが、これは凸集合の定義に出てきた式と同じですね。同様に3点で考えてみましょう。

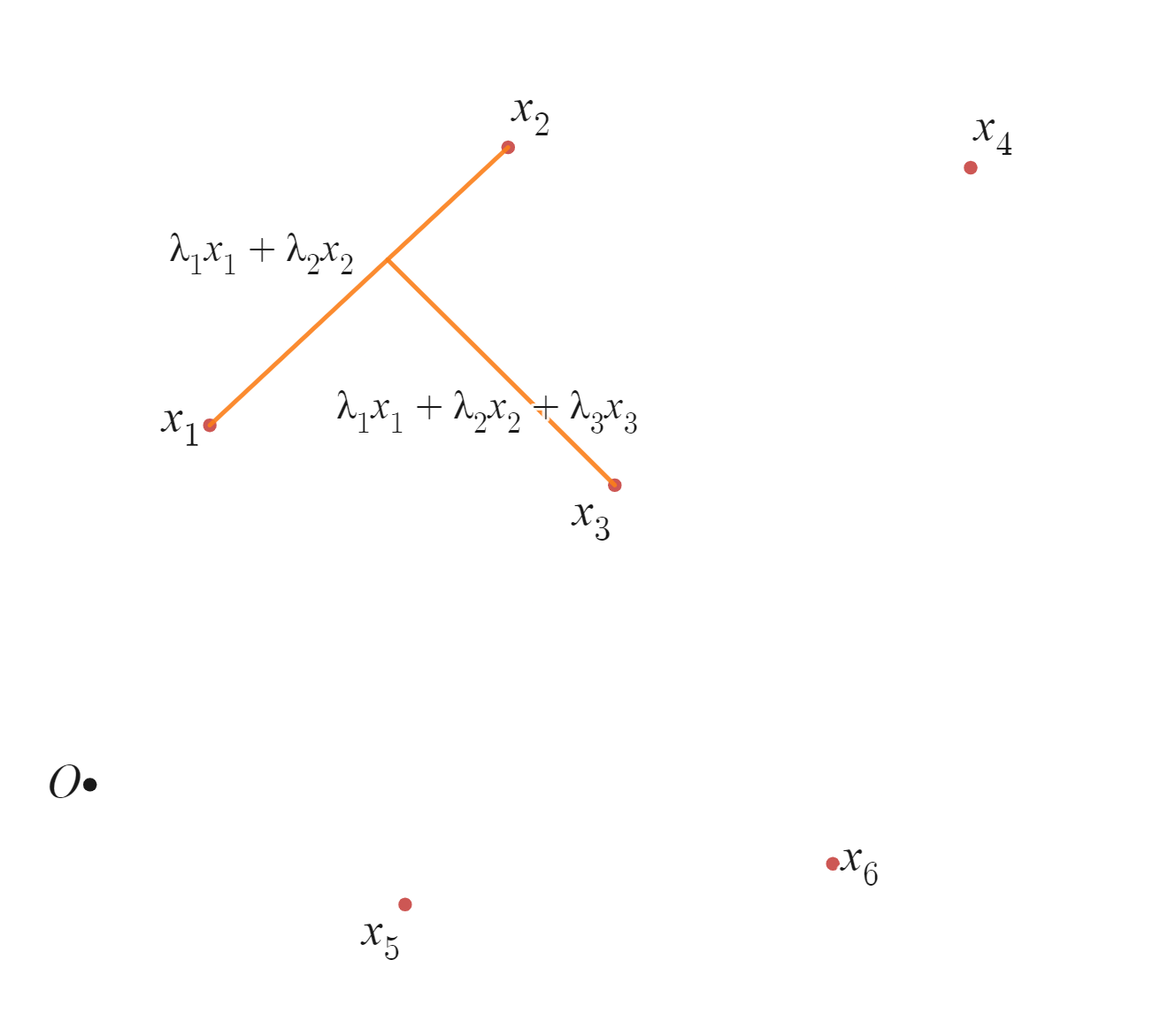凸結合（3点）

この図では$\lambda_1,\lambda_2$を固定しているようなイメージとなります。先ほどの2点$x_1,x_2$の凸結合を利用し、$x_3$との凸結合を考えてみましょう。先ほどの$\lambda_1,\lambda_2$を$\hat{\lambda_1},\hat{\lambda_2}$とし、新しく$0 \leq \lambda_3 \leq 1$を考えると、$(1 - \lambda_3)(\hat{\lambda_1} x_1 + \hat{\lambda_2} x_2) + \lambda_3 x_3$が3点の凸結合となります。ここで$\lambda_1 = (1 - \lambda_3)\hat{\lambda_1},\lambda_2 = (1 - \lambda_3)\hat{\lambda_2}$とおけば、3点の凸結合は$\lambda_1 x_1 + \lambda_2 x_2 + \lambda_3 x_3$と書けます。$\lambda_1 + \lambda_2 + \lambda_3 = (1 - \lambda_3)\hat{\lambda_1} + (1 - \lambda_3)\hat{\lambda_2} + \lambda_3 = (1 - \lambda_3) + \lambda_3 = 1$となることも確認できます。

凸結合（3点）2

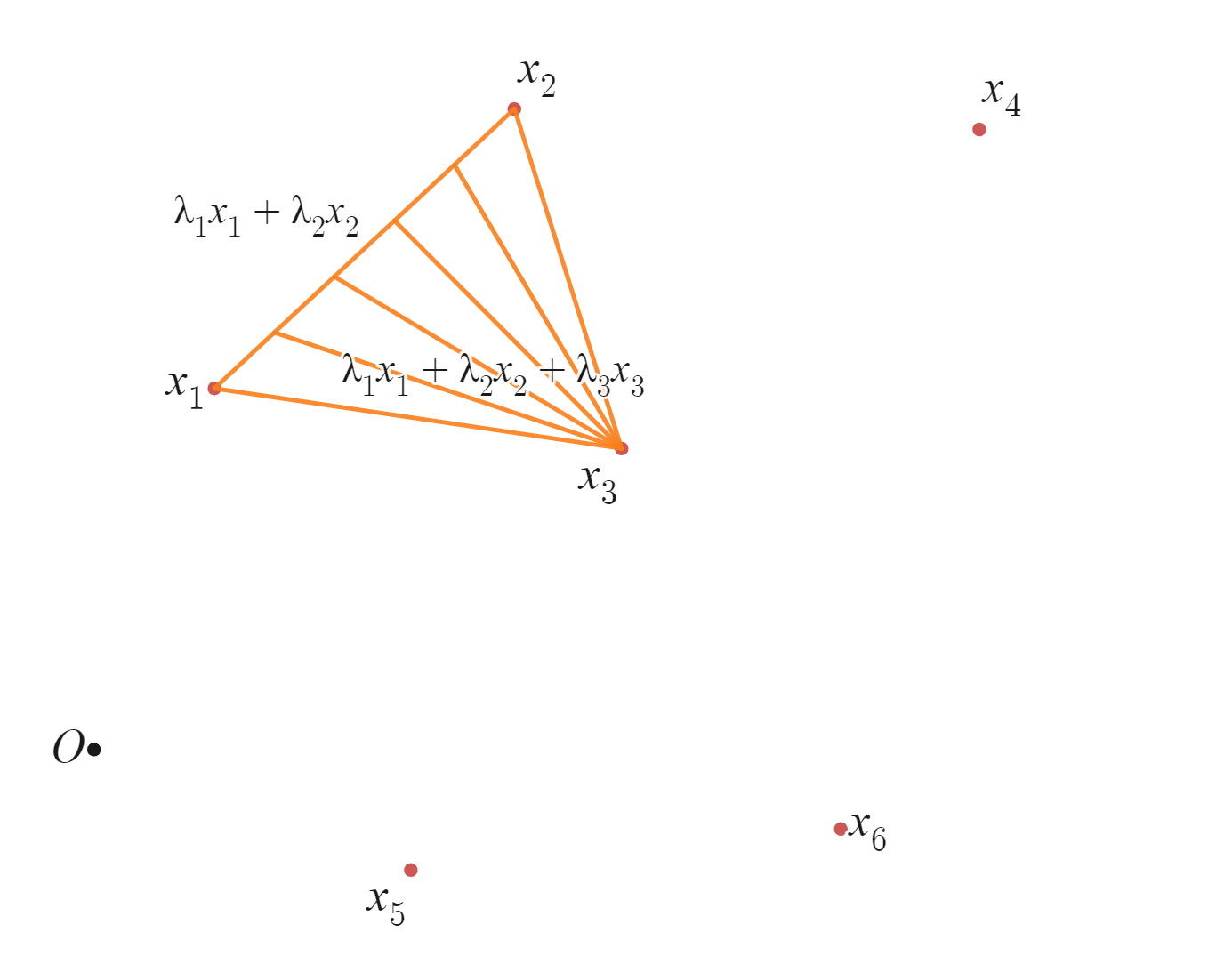
先ほどは$\lambda_1,\lambda_2$を固定しているようなイメージでしたが、この$\lambda_1,\lambda_2$を$0 \leq \lambda_1,\lambda_2 \leq 1$の範囲で動かしてみた図となります。3点$x_1,x_2,x_3$を頂点とする三角形内を占めるように見えますね。さらに同じように$x_4,x_5,x_6$と点を増やして見てみましょう。

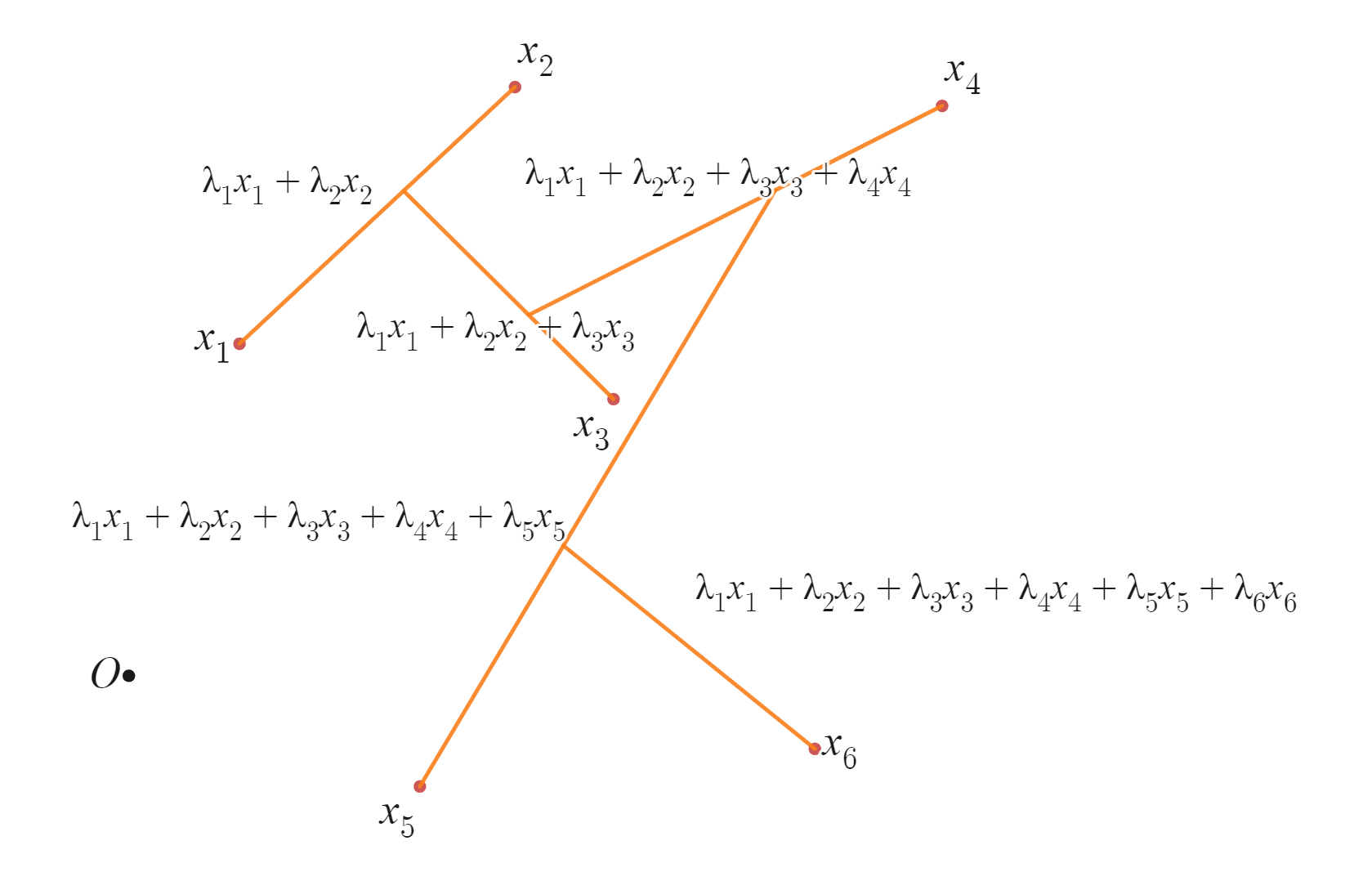凸結合（6点）

少しごちゃごちゃしているような感じですが、$x_1,x_2$から順々に考えていった場合の凸結合です。

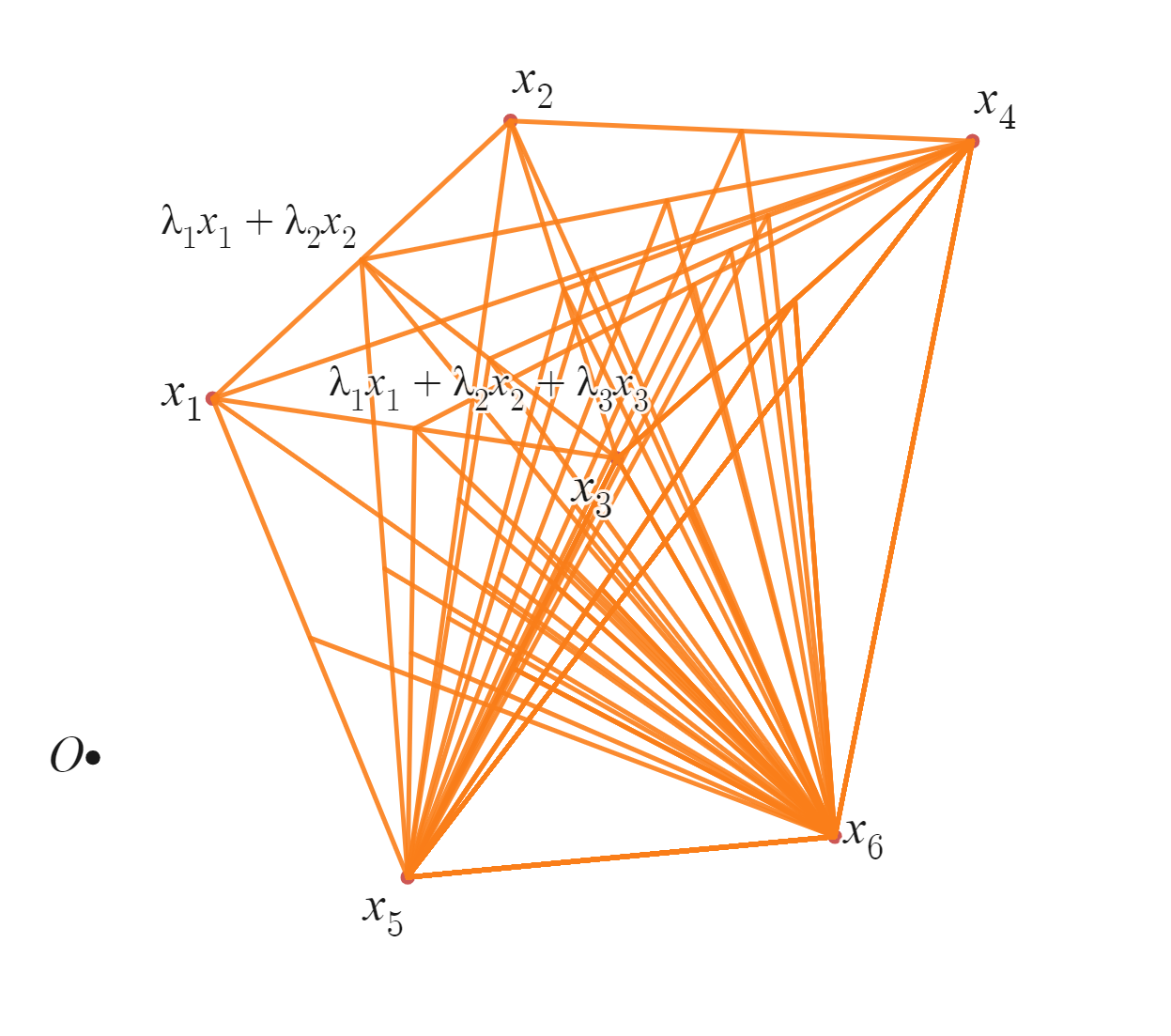凸結合（6点）2

3点の場合と同じように、各$\lambda$を動かしてみた場合の図です。この6点の凸結合をそれなりに表しているので、ある程度どのあたりが凸結合$\sum_{i=1}^{6} \lambda_i x_i$で表せる範囲なのかを見ることができます。この図から$x_3$は中にありますが、$x_1,x_2,x_4,x_5,x_6$を頂点とする多角形内を占めるように見えます。

凸結合と凸集合

ある集合が凸であることと、集合内の任意の点の凸結合がその集合に含まれることは同値となります。このことを示しているのが下記の命題です。

$C:convex$
$$\Leftrightarrow \forall c_1, \cdots ,c_n \in C, \sum_{i=1}^{n} \lambda_i c_i \in C \ (\lambda_1, \cdots ,\lambda_n \geq 0, \sum_{i=1}^{n} \lambda_i = 1)$$

＜証明の考え方＞
$(\Rightarrow)$について。
任意の$n$個の点について示したいので、数学的帰納法で示す。

$(\Leftarrow)$については凸集合の定義を思い出してみる。

$(\Rightarrow)$を示す。
数学的帰納法で証明する。

$i = 1$ のとき
$\forall c_1 \in C, \lambda_1 = 1$を考えると、
$\lambda_1 c_1 = c_1 \in C$ より明らか。
$i = 2$ のとき
$\forall c_1,c_2 \in C, \lambda_1 , \lambda_2 \geq 0, \lambda_1 + \lambda_2= 1$を考えると、
$C:convex$より$\lambda_1 c_1 + \lambda_2 c_2 \in C$となる。
$i = n-1$ のとき成り立つと仮定すると、
$$\sum_{i=1}^{n-1} \lambda_i c_i \in C \ (\lambda_1, \cdots ,\lambda_{n-1} \geq 0 , \sum_{i=1}^{n-1} \lambda_i = 1)$$
が成り立つ。
$c_n \in C, 0 \leq \hat{\lambda_n} \leq 1$をとると、$C:convex$より、
$$\hat{\lambda_n} c_n + (1 - \hat{\lambda_n}) \sum_{i=1}^{n-1} \lambda_i c_i \in C となる。$$
$(\hat{\lambda_n} + (1 - \hat{\lambda_n}) \sum_{i=1}^{n-1} \lambda_i = \hat{\lambda_n} + (1 - \hat{\lambda_n}) = 1,$
$ (1 - \hat{\lambda_n}) \lambda_i \geq 0 \ (\forall i = 1, \cdots ,n-1)となっている。)$
新しく$\hat{\lambda_i} = (1 - \hat{\lambda_n}) \lambda_i$とおくと、
$$\sum_{i=1}^{n} \hat{\lambda_i} c_i \in C \ (\sum_{i=1}^{n} \hat{\lambda_i} = 1, \hat{\lambda_1}, \cdots ,\hat{\lambda_n} \geq 0)$$
となるため、$i=n$でも成り立つことを示せた。

$(\Leftarrow)$を示す。
$n = 2$として考えると、
$\forall c_1,c_2 \in C, \lambda_1 + \lambda_2 = 1, \lambda_1,\lambda_2 \geq 0$に対して、$\lambda_1 c_1 + \lambda_2 c_2 \in C$となる。
これは$convex$の定義なので、$C:convex$を示すことができた。

ある集合が凸であることと、集合内の任意の点の凸結合がその集合に含まれることが同値であると示すことができましたが、凸集合でない場合について図で確認してみます。

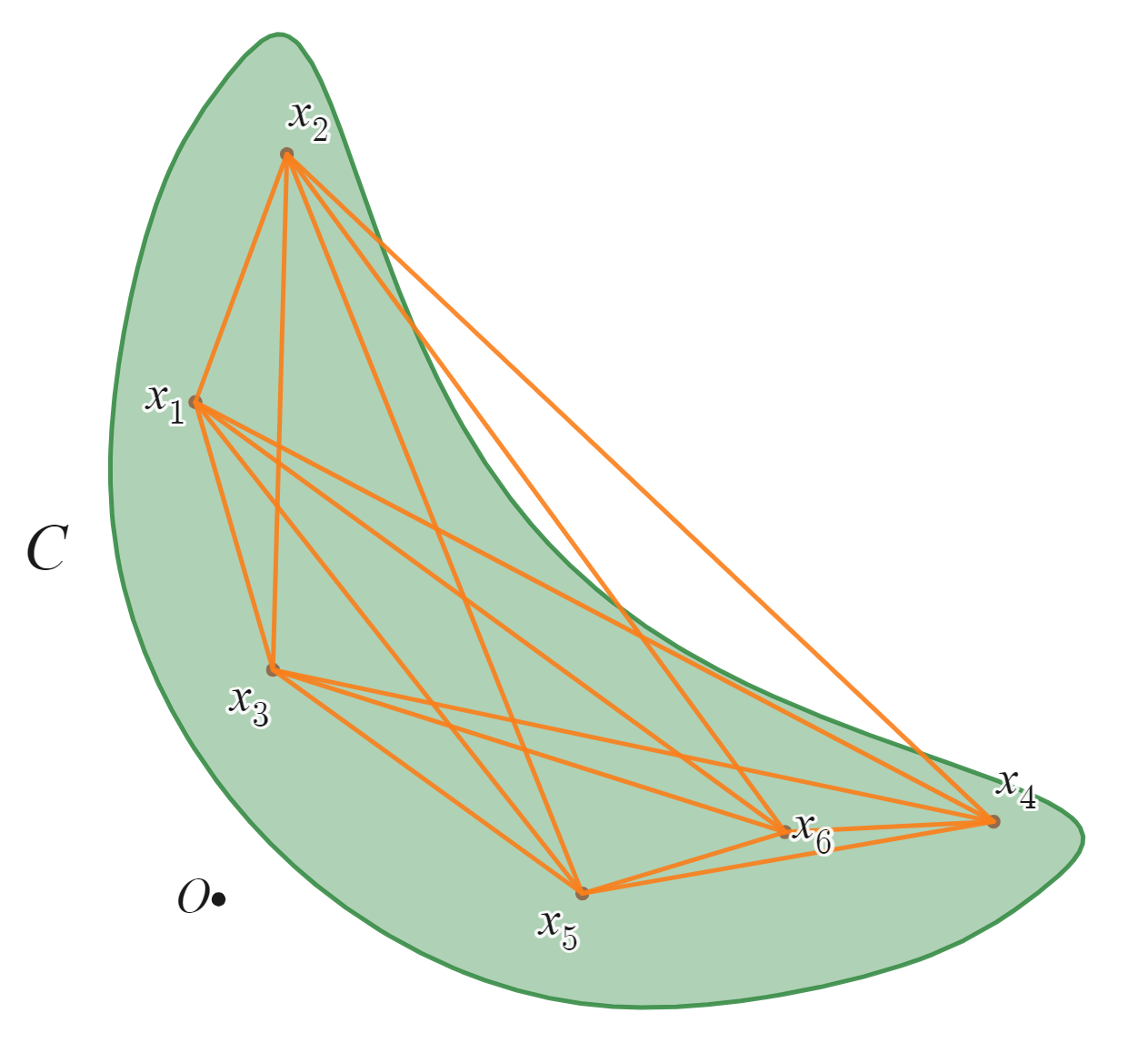凸でない集合内の点の凸結合