射影平面、アフィン平面の列挙
位数が素数pの場合で射影平面、アフィン平面のブロックデザインの列挙アルゴリズム
列挙方法
射影平面$p²+p+1$とアフィン平面$p²$の同時列挙方法
p=3の場合を例として説明いたします。
- $3²+3+1=13$を一次配列に格納$[0,1,2,3,4,5,6,7,8,9,10,11,12]$
- これを$0$を無限遠点として残して$3$つずつ区切ります。$[0|1,2,3|4,5,6|7,8,9|10,11,12]$
- まずは第一弾のブロックを列挙してきます。まずは$0$と区切りの$3$つの数列のペアを作ります。
$[0|1,2,3]$
$[0|4,5,6]$
$[0|7,8,9]$
$[0|10,11,12]$ - 続いて第二弾として前の記事で紹介したアフィン平面のブロックデザインの構築法を使います。$[1,2,3]$も無限遠点として考え、
$[4,5,6]$、
$[7,8,9]$、
$[10,11,12]$を$3²$のアフィン平面として$3×3$である配列の長さが平方分割した二次元配列とします。
($[4,5,6]$、$[7,8,9]$、$[10,11,12]$のアフィン平面のブロックデザインの構築は 自分なりのカークマンシステム をご覧下さい。) - 角度別の縦線、斜線にブロック分けした数列に先程の$0$のように先頭として点の$[1,2,3]$の無限遠点を置いて、アフィン平面のブロックをペアにする。
縦線
$[1|4,7,10][1|5,8,11][1|6,9,12]$
斜線y=x
$[2|4,8,12][2|5,9,10][2|6,7,11]$
斜線y=2x
$[3|4,9,11][3|5,7,12][3|6,8,10]$ - これで$3²+3+1=13$による13個の点と線とのブロックデザインが出来ます。
$[0,1,2,3]$
$[0,4,5,6]$
$[0,7,8,9]$
$[0,10,11,12]$
$[1,4,7,10]$
$[1,5,8,11]$
$[1,6,9,12]$
$[2,4,8,12]$
$[2,5,9,10]$
$[2,6,7,11]$
$[3,4,9,11]$
$[3,5,7,12]$
$[3,6,8,10]$
図で表すと↓のようになります。
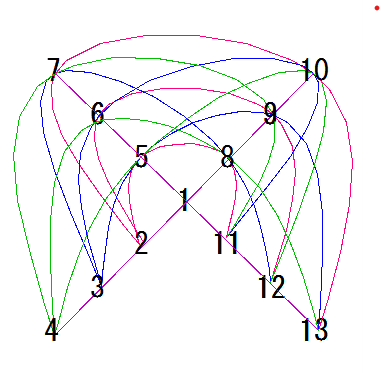p=3の射影平面の図(0〜12を1〜13に変えてます。)
でも点と線の数が同じなら、↓みたいな対称性のある図形が良いですね。
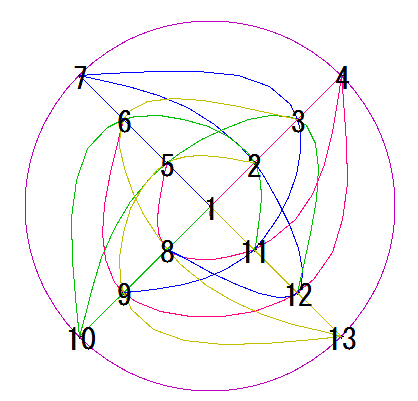対称性のあるp=3の射影平面の図
- また$3²+3+1$から$3+1$引いた数$3²$を第二弾のアフィン平面を同時に表示出来ます。
実装
javascriptで書いてみました。
pに好きな素数を入力すればそれに対応したブロックデザインが出来ます。
プログラミングは超初心者なので所々でツッコミたいと思いますが軽ーい気持ちで見てください。
webで実際に体験してみて下さい
pを選んで射影平面とアフィン平面ボタンを押せば表示します。
追記
位数は素数の累乗であれば可能なのですが、アルゴリズムにするとバックトラッキング法などで既にsagemath等で存在しますが、ある程度の知識が無いと自分みたいな初心者では難しいです。射影平面の標準構成ではまず使わないモノを沢山使ってめちゃくちゃクセ強になりました。
const p = 3
const q = p**2+p+1
const array=[ ]
for (let num = 0; num < q; num++) {
array.push(num);
}
const array1=[]
for(let i=1;i<=p;i++){
array1[i-1]=array.filter((value)=>{
if(p(i+1) >= value && pi < value){
return value;
}
});
};
const array0=[];
const afine=[ ];
for (let num = 1; num < q; num+=p) {
const u = function(u){
return array[num+u]
}
const l = function(u){
return array[num+u]-p-1
}
const datan = [0];
const dataa = [];
for(let h = 0; h < p; h++) {
datan[h+1]=u(h);
dataa[h]=l(h);
}//↓射影平面
array0.push(datan); //0とu(p-1)までを格納する
//↓アフィン平面
afine.push(dataa); //l(p-1)までを格納する
}
for(let i = 0; i < p; i++){
for (let num = 0; num < p; num++) {
const n = function(n){ //射影平面のアフィン平面部分に使用する関数
return array1[n][(num+i*n)%array1[n].length]
};
const a = function(n){ //アフィン平面に使用する関数
return array1[n][(num+i*n)%array1[n].length]-p-1
};
const ndata = [array[i+1]];
const adata = [];
for(let h = 0; h < p; h++) {
//↓射影平面
ndata[h+1]=n(h);
//↓アフィン平面
adata[h]=a(h);
}
array0.push(ndata); //[array[i+1]とn(p-1)までを格納する
afine.push(adata); //a(p-1)までを格納する
afine[0]='';
}};
console.log(array0);
console.log(afine);
この記事を高評価した人
この記事に送られたバッジ
投稿者
