◼️コラッツ予想が正であることの証明のアイデア

はじめに

閲覧ありがとうございます。
私は初めてmathlogを利用するため、読みづらい部分があることをご了承下さい。
私はこの証明に自信を持っていますが、あくまで下書きのような段階ですので論理に間違いがある可能性が高いです。
是非、ご指摘・ご意見を下さい。
複数の奇数の型にaを登場させていますが、これは都合上そう表記しているだけであり、実際の数は型によって異なります。

1.コラッツ予想についての説明

ある自然数$n$があるとします。
$n$が偶数ならば、$\frac{n}{2}$
$n$が奇数ならば、$3n＋1$
という動作を繰り返すことで、1に帰着するのではないかという予想です。

2.証明の流れ

①奇数を型に分類する。
②全ての奇数の型が4a＋1型の奇数に帰着することを示す。
③4a＋1型の奇数が1に帰着することを証明する。
この3つの流れです。

3.奇数の型について

まず、奇数は2a＋1（aは正の整数）という型に大きく分類されます。
2a＋1型の奇数についてコラッツ動作を2回行います。

3→10→5
5→16→8
7→22→11
9→28→14
11→34→17
13→40→20
15→46→23
17→52→26

結果を見てみると偶数になるか奇数になるかに分かれていると分かります。
そのため、2a＋1型を4a＋1型と4a＋3型に分けます。
4a＋1（1、5、9、13、17…）→偶数
4a＋3（3、7、11、15、19…）→奇数

4a＋1型について

4a＋1についてコラッツ動作を行います。

4a＋1→12a＋4→6a＋2

確かに、6a＋2は偶数です。更に動作を続けると、3a＋1となり元の数より小さくなっていることも分かります。

4a＋3型について

4a＋3型の奇数にコラッツ動作を2回行います。

3→10→5
7→22→11
11→34→17
15→46→23
19→58→29
23→70→35
27→82→41
31→94→47

結果が4a＋1型か4a＋3型に分かれています。
また4a＋3型を分類分けします。

8a＋3（3、11、19、27、35）→4a＋1
8a＋7（4、15、23、31、39）→4a＋3

8a＋3型について

8a＋3型が4a＋1型に、コラッツ動作を2回行うことで変換されることを確かめます。

8a＋3→24a＋10→12a＋5

12a＋5が4b＋1に変換されるか等号で示します。

\begin{equation} \begin{aligned} 4b + 1 &= 12a＋5 \\ 4b &= 4（3a＋1）\\ 　　　　　　b &＝ 3a＋1 \\ \end{aligned} \end{equation}

b＝3a＋1が成り立ち、bはaがどのうよな正の整数であっても、正の整数であることを確かめられたので、8a＋3型が2回のコラッツ動作で4a＋1型に変換されることが示されました。
これは、8a＋3型から4a＋1型へと、型を降りることができることを表しています。

8a＋7型について

8a＋7型でも、4a＋3型と同様のことができるかを確かめます。
8a＋7型を2つに分類します。

16a＋7型（7、23、39、55…）→8a＋3型
16a＋15型（15、31、47、63…）→4a＋3型

16a＋7型について

16a＋7にコラッツ動作を2回行います。

16a＋7→48a＋22→24a＋11

24a＋11が8b＋3と等号で結ばれることを確かめます。

\begin{equation} \begin{aligned} 8b＋3 &= 24a＋11 \\ 8b &= 8（3a＋1）\\ 　　　　　b &＝ 3a＋1 \end{aligned} \end{equation}

またb＝3a＋1が現れましたね。
よって16a＋7型はコラッツ動作を2回行うことで、8a＋3型へと変換することができるということが分かりました。
これは無限に行うことができます。
そのため、4a＋1型以外の型の奇数が必ず4a＋1型に帰着することを示したいと思います。

任意の奇数の型について

4a＋1型に帰着する型は現在判明している型で、8a＋3型と16a＋7型が分かっています。
この規則性に従えば、32a＋15型、64a＋31型…と続くはずです。

4a＋1を1番目の奇数の型とすると、p番目の奇数の型は（pは自然数）

となります。

$$ 2^{p＋1}a＋ 2^{p}−1 $$
についてコラッツ動作を行います。

$$ 2^{p＋1}a＋ 2^{p}−1 $$
　　　↓（3倍＋1）
$$ 3×2^{p＋1}a＋ 3×2^{p}−2 $$
　　　　　↓（$\frac{1}{2}$倍）
$$ 3×2^{p}a＋ 3×2^{p−1}−1 …① $$

①とp−1番目の型の奇数を等号で結べるのか確かめます。

p−1番目の型は
$$ 2^{p}a＋ 2^{p−1}−1 $$

ここからの式展開は複雑のため、画像です。
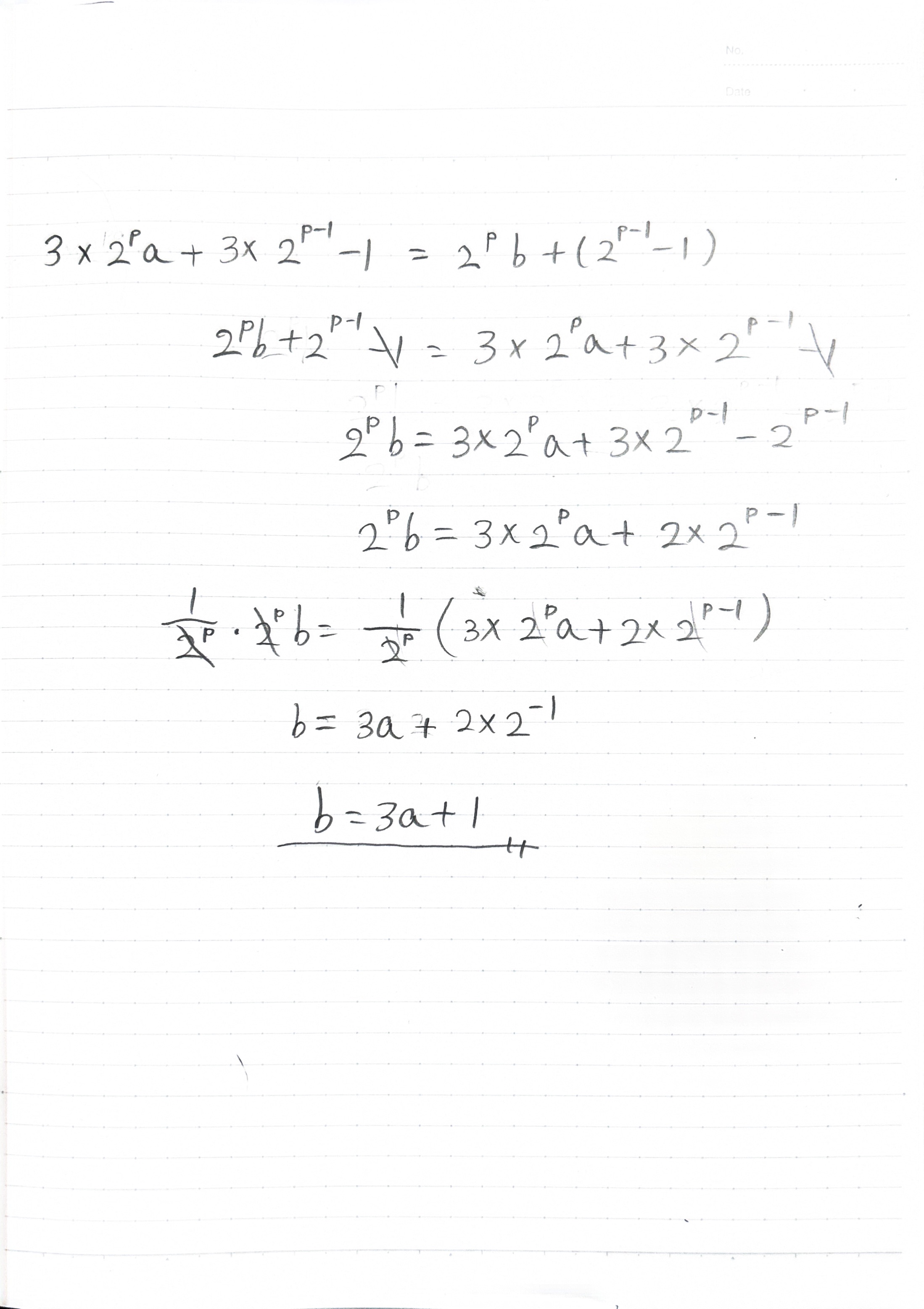p番目の型からp−1番目の型への変換

この画像から結果がまた、b＝3a＋1となり、変換が可能であることが分かります。
さらにpが結果の式に含まれないため、pの値に関係なく変換が行われることが分かります。（4a＋1型を除く）

つまり、
p番目→p−1番目→p−2番目…→4a＋1型と、奇数がどの型に分類されていたとしても、必ず4a＋1型に帰着することが示されました。

3.直通奇数について

4a＋1型が1になることを証明したいところですが、その前に必要な知識があります。

ある奇数に3をかけて1を足すと、$2^{n}$となります。（nは自然数）
これは、その奇数が1回の増加の後、1に帰着するまで減少を続けるということです。
その奇数のことを私は直通奇数と呼びます。
直通奇数をkとして式を求めます。
\begin{align} 3k＋1 &= 2^{n} \\ k &= \frac{2^ {n}-1}{3} \end{align}
kが自然数になるときと、ならないときがあるので数を整えると、

となります。

合流直通奇数について

直通奇数の中でも他の型の奇数が合流可能な直通奇数があります。私はその数を合流直通奇数と呼びます。
以下は略して合直奇数と呼びます。
合直奇数は2（mod3）となります。

直通奇数について3を法として考えると
2→0→1→2→0→1…という循環があることが分かります。
つまり、n＝3m−1（mは自然数）となるときが合直奇数です。
式にすると、

となります。

また、直通奇数は必ず4a＋1型の奇数になります。
これは、コラッツ動作で2回以上減少を最初に行う奇数が、4a＋1型の奇数にしか存在しないためです。
合直奇数は4a＋1型に存在する。
これが後に重要になってきます。

4.4a＋1型の奇数が1に帰着することの証明

4a＋1型の奇数で、1に帰着しない奇数が存在すると仮定し、その数をfとします。

fは無限に4a＋1型の奇数を通過します。
これは、どんな型の奇数でも4a＋1型の奇数に必ず帰着するためであり、1に帰着しないならば、必ず4a＋1型の奇数を無限に通過することになります。
また、fが通過する奇数は決して重複しません。$\frac{1}{2}$倍と、3倍＋1で、1倍を合成することは不可能であるためです。

つまり、fは全ての4a＋1型を通過することになります。

そのため、必然的にfは合直奇数を通過することになります。

合直奇数を通過する場合
fは1に帰着する→fの仮定に反する。

合直奇数を通過しない場合
fは無限回通過をしていな。→fの仮定に反する

仮定に矛盾が発生するので、fは存在しません。

これで、4a＋1型は1に帰着することが証明されました。

5.結論

①全ての奇数は
$$ 2^{p＋1}a＋ 2^{p}−1 $$
という型に分類される。
②全ての奇数は、4a＋1型に帰着する。
③4a＋1型は必ず合直奇数と繋がり、1に帰着する。

この3つから、奇数が必ず1に帰着することが示されました。
偶数も有限回2で割ることで奇数になるため、同様のことが言えます。

結論として、自然数は1に帰着する。

コラッツ予想が正であることを証明できました。

6.最後に

ここまで読んで下さりありがとうございました。^_^
正解不正解はともかく、かなりエレガントな解答だと私は思っています。
ご意見・ご指摘などがありましたら、ぜひコメント下さい。

7.追記

「コラッツ予想で循環する数が1のみであることの証明のアイデア」
という関連記事を書きました。
お時間があればぜひご覧になってください。

https://mathlog.info/articles/Uur1KKKEUAE1GurN5JlS