等差×等比に効く！ 瞬間部分和分！

はじめに

この記事で紹介する、瞬間部分積分ならぬ瞬間"部分和分"を使うと$\displaystyle\sum_{k=0}^{n-1}k^2 \cdot2^k$のようなちょっと面倒な数列の和でも
$$ \sum_{k=0}^{n-1}k^2 \cdot2^k=\sum\nolimits_0^nk^2\cdot 2^k\delta k=\l[\l(k^2-\l(2k+1\r)\cdot 2+2\cdot 2^2\r)2^{k}\r]_{0}^{n} =\l(n^2-4n+6\r)\cdot 2^n-6 $$
と簡単に計算できます。なお記述試験の答案に書くときは
「$f(k)=\l(k^2-4k+6\r)\cdot 2^k$とおくと$f(k+1)-f(k)=k^2\cdot 2^k$であるから」
などと書けばよいと思います。要するに和の中抜けになるような関数（不定和分）を簡単に求めるのが瞬間部分和分です。
なお、どうしてこんなことを考えたかというと、多項式×等比数列の総和が多項式×指数関数の積分みたいに簡単に求められたら楽だと思ったからです。

記号

がーと さんの 高校数学の数列と微分積分は似ているという話（和分差分） がわかりやすかったので一部そこで使われていた記号を使います。

$f\l(x\r) $を$x\in \mathbb{Z} $の関数（すなわち数列）として、
\begin{align*} &\Delta f\l(x\r)=f\l(x+1\r)-f\l(x\r)& \text{（前進差分）}\\ &\nabla f\l(x\r)=f\l(x\r)-f\l(x-1\r)& \text{（後退差分）} \end{align*}
と定めます。
また、$\Delta ^{n+1}f\l(x\r)= \Delta \l(\Delta ^n f\l(x\r)\r)$とします。
$x $の差分であることを強調するため$\Delta f\l(x\r) $を$\Delta _xf\l(x\r) $と表すことがあります。
$f\l(x\r) $に対し、$\Delta F\l(x\r)=f\l(x\r) $となる$F\l(x\r) $（の一つ）を$\Delta ^{-1}f\l(x\r) $と書きます。
同様に$\nabla^{-1}f\l(x\r) $を定めます。

$\sum\nolimits_a^b f\l(x\r) \delta x $は$\displaystyle\sum_{x=a}^{b-1}f\l(x\r) $を表すものとします。
このとき以下が成り立ちます。（差分和分学の基本定理）
$$ \Delta _x\l(\sum\nolimits_a^x f\l(t\r) \delta t\r)=\Delta \l(\sum_{t=a}^{x-1} f\l(t\r)\r)=\sum_{t=a}^{x} f\l(t\r)-\sum_{t=a}^{x-1} f\l(t\r)=f\l(x\r) $$
$$ \sum \nolimits_a^x \Delta _t f\l(t\r)\delta t=\sum_{t=a}^{x-1} \l(f\l(t+1\r)-f\l(t\r)\r)=f\l(x\r)-f\l(a\r) $$
2つ目の式を積分のように
$$ \sum \nolimits _a^x \Delta f\l(t\r)\delta t=\l[f\l(t\r)\r]_a^x=f\l(x\r)-f\l(a\r) $$
と書くことがあります。また、この式から$\Delta ^{-1}f\l(x\r) $を$\sum_{}^{} f\l(x\r)\delta x $と書き、不定和分と呼びます。

積の差分法

これより
$$ f\l(x\r)\Delta g\l(x\r)=\Delta \l(f\l(x\r)g\l(x\r)\r)-\l(\Delta f\l(x\r)\r)g\l(x+1\r) $$
を得る。$\Delta G\l(x\r)=g\l(x\r) $なる$G $をとり、上の式の$g $を$G $にすると
$$ f\l(x\r)g\l(x\r)=\Delta \l(f\l(x\r)G\l(x\r)\r)-\l(\Delta f\l(x\r)\r)G\l(x+1\r) $$
両辺$x $で和分すると
$$ \sum_{}^{} f\l(x\r)g\l(x\r)\delta x=f\l(x\r)G\l(x\r)-\sum_{}^{} \Delta f\l(x\r)G\l(x+1\r)\delta x $$
（部分和分の公式）
を得る。定和分を考えると
$$ \sum\nolimits_a^b f\l(x\r)g\l(x\r)\delta x=\l[f\l(x\r)G\l(x\r)\r]_a^b -\sum \nolimits _a^b \Delta f\l(x\r)G\l(x+1\r)\delta x $$
を得る。（アーベルの総和公式）

瞬間部分和分の導出

アーベルの総和公式は部分積分の公式
\begin{align*} \int f\left(x\right)g\l(x\r)dx=f\l(x\r)G\l(x\r)-\int f'\l(x\r)G\l(x\r)dx \end{align*}
に似ていることから部分和分の公式と呼べるものです。
この記事で扱う瞬間部分和分はアーベルの総和公式を繰り返し使うことによって導出できるのですが、それだと分かりづらくなると思ったので差分を和分することによって直接示します。

いわゆる瞬間部分積分と同じように、下のような表を書くと分かりやすいです。なお、$g $を$G_0 $にする変形では$\Delta ^{-1} $、それ以降では$\nabla^{-1} $となります。
あと実際の計算では$G_{-1}$は出てきません。
$g\l(x\r)=G_{-1}\l(x+1\r)=\nabla G_0\l(x+1\r)=G_0 \l(x+1\r)-G_0 \l(x\r)=\Delta G_0 \l(x\r) $
のため、1行目の変形では$\Delta^{-1} $が現れます。
「さ」が差分する方、「わ」が和分する方を表します。

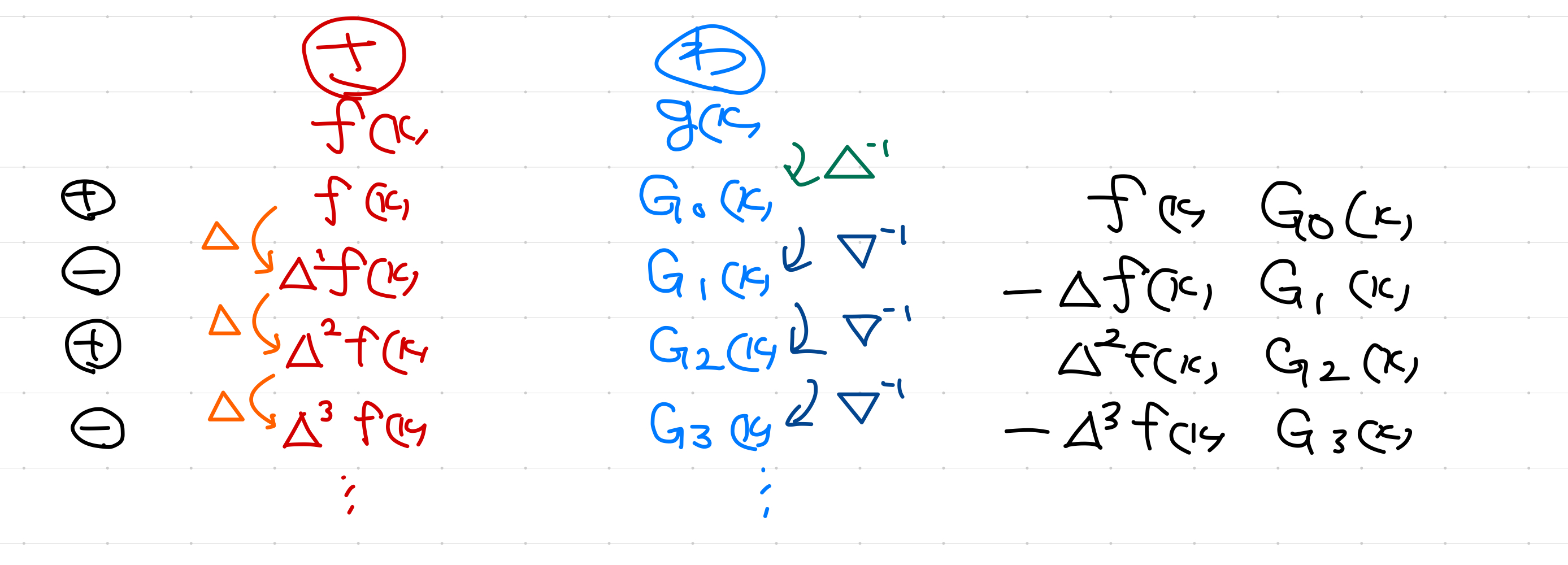瞬間部分和分の表

基本的な差分、和分公式

1回差分をとるごとに次数が1下がるので$n$次関数は$n+1$回差分をとると0になります。
$\Delta x^n$の公式については$(x+1)^n -x^n$を計算しているだけです。

これらの公式を使い倒していきます。

まずは不定和分！！！

積分の場合に不定積分を先に考えるのと同じように不定和分を先に考えます。
なお、積分と同じで不定和分の方が定和分より楽しいです。

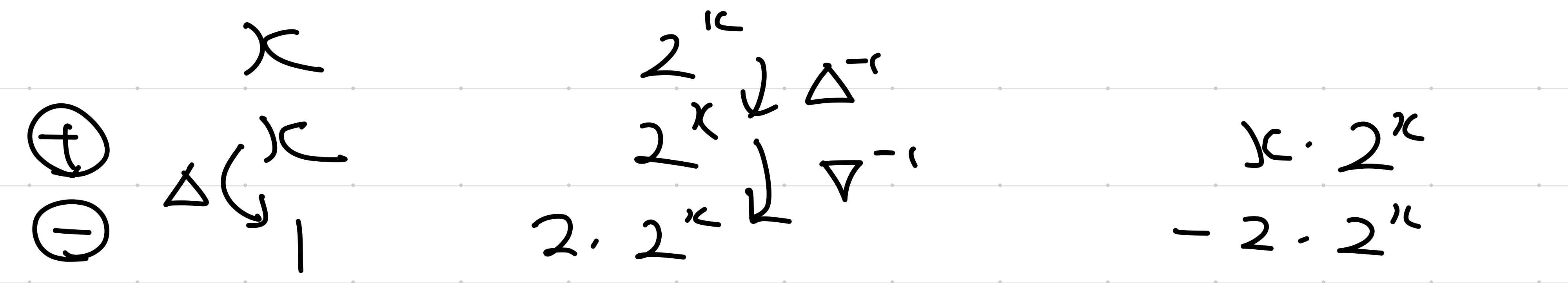表はこんな感じ

$\sum_{}^{} x\cdot 2^x = \l(x-2\r)\cdot 2^x+C$ （$C$は和分定数）

実際、
$\Delta \l(\l(x-2\r)\cdot 2^x \r)=\l(2\l(x-1\r)-\l(x-2\r)\r)\cdot 2^x =x\cdot 2^x $

なお、慣れてきたら瞬間部分積分と同様、表を書かずとも答えを求められるようになります。
表を書いても書かなくても、検算は（結構ミスりそうなポイントが多いので）した方がいいと思います。検算して正しければ確実です。

\begin{align*} \sum_{}^{} x^3 a^x = \l(x^3 -\frac{a}{a-1}\l(3x^2 +3x+1\r)+\l(\frac{a}{a-1}\r)^2 \l(6x+6\r)-6\l(\frac{a}{a-1}\r)^3 \r)\frac{1}{a-1}a^x+C \end{align*}

$\frac{1}{a-1}a^x$でくくると分かりやすいです。

$\sum x^2 3^x \delta x$
瞬間部分和分を使えば、書き並べて階差数列を何度もとったり和の中抜けになりそうな$(ax^2+bx+c)3^x$の形を仮定して係数比較したりするよりも圧倒的に速く和を求めることができます。

$\sum x^3 2^{-x}\delta x $
なお、$\Delta \l(3x^2+3x+1\r)=3\l(2x+1\r)+3=6x+6 $と計算しています。
検算します。普通に計算すると$(x+1)^n$の形がたくさん出てきて展開が大変なので組立除法を使って工夫します。
検算

定和分

ここからは定和分、つまり実際に問題に出される形の数列の和を求めていきます。定積分と同様に不定和分に代入することで求められます。
不定和分で得た結果を使っていきます。

\begin{align*} \sum_{k=1}^{n} k\cdot 2^k=\sum \nolimits_1^{n+1}k\cdot 2^k \delta k = \l[\l(k-2\r)\cdot 2^k \r]_1^{n+1} =\l(n-1\r)\cdot 2^{n+1}+2 \end{align*}
と求められます。
とはいえこのままだと他の人がわからないので、実際の記述試験であれば和の中抜けの考え方で
「$f\l(k\r)=\l(k-2\r)\cdot 2^k $とおくと
\begin{align*} \sum_{k=1}^{n} k\cdot 2^k =\sum_{k=1}^{n} \l(f\l(k+1\r)-f\l(k\r)\r)=f\l(n+1\r)-f\l(1\r)=\l[\l(k-2\r)\cdot 2^k\r]_1^{n+1}=\l(n-1\r)\cdot 2^{n+1}+2 \end{align*}
」のように書いたほうがいいと思います。マーク式であれば自分しか見ないので最初の書き方でいいです。

x23xで$k^2 \cdot 3^k$の不定和分（の一つ）$f\l(x\r)=\frac{1}{2}\l(x^2-3x+3\r)\cdot 3^x $を得たのでこれを使います。
\begin{align*} \sum_{k=1}^{n} k^2 \cdot 3^k &= \sum_{k=0}^{n-1} k^2 \cdot 3^k + n^2 \cdot 3^n = \sum_{k=0}^{n-1} (f(k+1) - f(k)) + n^2 \cdot 3^n \\ &= f(n) - f(0) + n^2 \cdot 3^n \\ &= \left[ \frac{(k^2 - 3k + 3) \cdot 3^k}{2} \right]_{k=0}^{n} + n^2 \cdot 3^n \\ &= \frac{(n^2 - 3n + 3) \cdot 3^n}{2} + n^2 \cdot 3^n-\frac32 \\ &= \frac{(n^2 - n + 1) \cdot 3^{n+1}}{2} - \frac{3}{2} \end{align*}

$f\l(x\r)=\frac{1}{2}\l(x^2-3x+3\r)\cdot 3^x $に$1 $や$n+1 $を入れるよりも、$0 $や$n $を入れるほうが圧倒的に楽なので、先に代入しやすい形にするのがポイントです。
なお、$l=k-1 $などと変換する方法もありますが、多項式の次数が大きくなるとこの方法も大変です。
なので個人的にはこのように最後の項だけ分離するのが楽だと思います。

x32xで$x^3 2^{-x}$の不定和分（の一つ）$f(x)=-\l(x^3 +3x^2 +9x+13\r)\cdot 2^{-x+1}$を得たのでこれを使っていきます。
\begin{align*} \sum_{k=1}^{\infty} k^3 \cdot 2^{-k} = \sum_{k=1}^{\infty} \left( f(k+1) - f(k) \right) = \left[ f(k) \right]_1^\infty = -f(1) = 26 \end{align*}

無限和であれば$f$が$0$になって大分楽に求められます。
なお微分を使って求める方法もありますが、あちらは和の極限と積分の交換をする必要があってややこしいので記述試験で書く場合はこちらの方が楽です。

応用公式

それぞれ左の式から右の式が求まります。
指数を分けてから計算するより速く求められます。

\begin{align*} & \sum_{k=1}^{n} (2k-1) \cdot 2^{2k-1} = \sum_{k=1}^{n+1} (2k-1) \cdot 2^{2k-1} \delta k \\ &= \left[ \l(2k-1-2\cdot \frac{4}{3}\r)\cdot \frac{1}{3}2^{2k-1}\right]_{1}^{n+1} \\ &= \frac{1}{3} \left[ \l(2k-\frac{11}{3}\r) \cdot 2^{2k-1} \right]_{1}^{n+1} \\ &= \frac{1}{3} \left( \l(2(n+1)-\frac{11}{3}\r) \cdot 2^{2n+1} - \left(-\frac{5}{3}\right) \cdot 2 \right) \\ &= \frac{1}{3} \left( \l(2n-\frac{5}{3}\r) \cdot 2^{2n+1} + \frac{10}{3} \right) \end{align*}

参考文献

高校数学の数列と微分積分は似ているという話（和分差分）