トーラスのEuler標数を微分幾何で計算

2次元トーラス$T^2$のEuler標数をGauss-Bonnetの定理によって微分幾何学的に計算し，位相幾何学的な結果と比較します．

Euler標数と大域版Gauss-Bonnetの定理

$\chi(S)$は$S$の位相不変量になっています．つまり曲面の形状や曲がり方（曲率）とは関係のない，位相幾何学的な量です．しかし，次の大域版Gauss-Bonnetの定理はGauss曲率の全積分という微分幾何学的な量からEuler標数を得ることができると主張します．

$\chi(T^2)$を微分幾何的に計算

大半径$R$,小半径$r$をもつトーラス$T^2$は次のようにパラメタ表示できます．
$$x\colon (-\pi,\pi)^2\to\R^3$$

$$x(u^1,u^2)= \begin{pmatrix} (R+r\cos{u^1})\cos{u^2}\\ (R+r\cos{u^1})\sin{u^2}\\ r\sin{u^1} \end{pmatrix} $$

まず接ベクトル場は，
$$B_1(u^1,u^2)=\del_1x(u^1,u^2)= \begin{pmatrix} -r\sin{u^1}\cos{u^2}\\ -r\sin{u^1}\sin{u^2}\\ r\cos{u^1} \end{pmatrix} $$
$$B_2(u^1,u^2)=\del_2x(u^1,u^2)= \begin{pmatrix} -(R+r\cos{u^1})\sin{u^2}\\ (R+r\cos{u^1})\cos{u^2}\\ 0 \end{pmatrix} $$
となります．よって，
$$(B_1\times B_2)(u^1,u^2)=r(R+r\cos{u^1}) \begin{pmatrix} \cos{u^1}\cos{u^2}\\ \cos{u^1}\sin{u^2}\\ \sin{u^1} \end{pmatrix} $$
$$\|(B_1\times B_2)(u^1,u^2)\|=r(R+r\cos{u^1})$$
であるので，単位法ベクトル場は，
$$N(u^1,u^2)=\begin{pmatrix} \cos{u^1}\cos{u^2}\\ \cos{u^1}\sin{u^2}\\ \sin{u^1} \end{pmatrix}$$
となります．また第一基本量は，
$$g_{11}=\yam{B_1,B_1}=r^2$$
$$g_{12}=g_{21}=\yam{B_2,B_1}=0$$
$$g_{22}=\yam{B_1,B_1}=(R+r\cos{u^1})^2$$
で与えられます．次に第二基本量を計算します．まず
$$\del_1 B_1(u^1,u^2)= \begin{pmatrix} -r\cos{u^1}\cos{u^2}\\ -r\cos{u^1}\sin{u^2}\\ -r\sin{u^1} \end{pmatrix} $$
$$\del_2 B_1(u^1,u^2)= \begin{pmatrix} r\sin{u^1}\sin{u^2}\\ -r\sin{u^1}\cos{u^2}\\ 0 \end{pmatrix} $$
$$\del_2 B_2(u^1,u^2)= \begin{pmatrix} -(R+r\cos{u^1})\cos{u^2}\\ -(R+r\cos{u^1})\sin{u^2}\\ 0 \end{pmatrix} $$
なので，
$$h_{11}=\yam{\del_1 B_1,N}=-r$$
$$h_{12}=h_{21}=\yam{\del_2 B_1,N}=0$$
$$h_{22}=\yam{\del_2 B_2,N}=-(R+r\cos{u^1})\cos{u^1}$$
を得ます．従ってshape作用素の表現行列は，
\begin{align} A(u^1,u^2)&= \begin{pmatrix} g_{11}& g_{12}\\ g_{21}& g_{22} \end{pmatrix}^{-1} \begin{pmatrix} h_{11}& h_{12}\\ h_{21}& h_{22} \end{pmatrix}\\ &= \begin{pmatrix} r^2& 0\\ 0& (R+r\cos{u^1})^2 \end{pmatrix}^{-1} \begin{pmatrix} -r& 0\\ 0& -(R+r\cos{u^1})\cos{u^1} \end{pmatrix}\\ &= \begin{pmatrix} -\frac{1}{r}& 0\\ 0& -\frac{\cos{u^1}}{(R+r\cos{u^1})} \end{pmatrix}\\ \end{align}
となります．よってGauss曲率は，
$$K(u^1,u^2)=\det{A(u^1,u^2)}=\frac{\cos{u^1}}{r(R+r\cos{u^1})}$$
で与えられます．これを全体で積分します．
\begin{align} \int_{T^2} K\;dA &=\int_{-\pi}^{\pi}\int_{-\pi}^{\pi}K(u^1,u^2)\|(B_1\times B_2)(u^1,u^2)\|du^1du^2\\ &=\int_{-\pi}^{\pi}\int_{-\pi}^{\pi} \frac{\cos{u^1}}{r(R+r\cos{u^1})}r(R+r\cos{u^1})du^1du^2\\ &=\int_{-\pi}^{\pi}\int_{-\pi}^{\pi} \cos{u^1}du^1du^2\\ &=0\cdot2\pi=0 \end{align}
よって大域版Gauss-Bonnetの定理から，
$$\chi(T^2)=\frac{1}{2\pi}\int_{T^2}K\;dA=0$$
を得ることができます．

位相幾何による結果との比較

$g$人乗りの浮き輪のような閉曲面（正確には$T^2$の$g$個の連結和$T^2\#\cdots\#T^2$）を種数$g$の向き付け可能な閉曲面といい，$\Sigma_g$で表します．但し，$\Sigma_0=S^2$とします．
種数$g$の向き付け可能な閉曲面$\Sigma_g$
$\Sigma_g$は$\Sigma_{g-1}$にハンドル$H$を1つ連結して得られます．
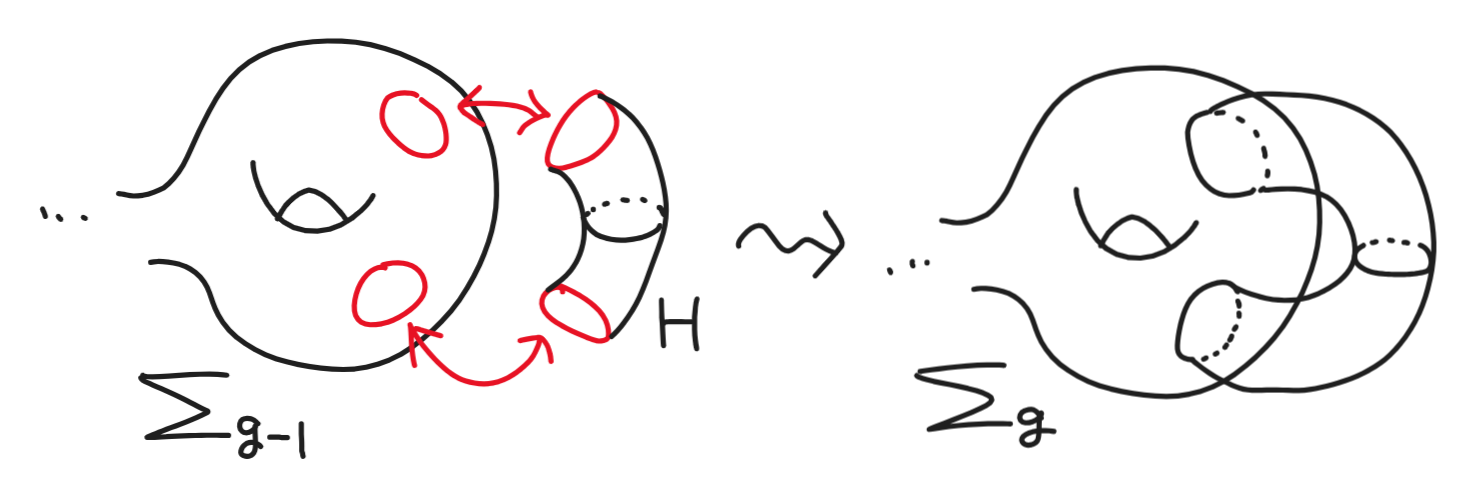ハンドルの連結
ハンドルを1つ連結するとEuler標数は2小さくなる事実と$\chi(\Sigma_0)=\chi(S^2)=2$から次がいえます．

$T^2=\Sigma_1$なので，$\chi(T^2)=0$を得ることができます．Gauss-Bonnetの定理による結果と整合することが確認できました．