量子エラー訂正符号とホモロジー

0. はじめに

　みなさん初めまして。Jimmyといいます。
　今回は駒場理数サークルの 豚汁カレンダー 15日目の記事として、量子エラー訂正符号、特にCSS符号をホモロジーの観点から扱う手法について紹介したいと思います。
　Shorのアルゴリズムなどが発見されて以降、量子コンピューターは精力的に研究されていましたが、最近になって様々なハードウェア会社が、◯◯年頃に◯◯万ビットの量子コンピューターを作ります！のように宣伝を始めていて、いよいよ実用化も近づいてきているでしょうか。
　そんな量子コンピューターですが、現状、古典コンピューターと比べてはるかにエラーの発生確率が高くなってしまっています。エラー訂正機能のない量子コンピューター（NISQ）も一部の問題で古典コンピューターを超えることが期待されていますが、より広範な問題を扱うためには、エラーに耐性をもった量子コンピューター（FTQC）が必要だとされています。エラー訂正の方式は様々なものが提案されていますが、本記事では特にCSS符号と呼ばれるクラスに焦点を当て、それがホモロジーを使うことで簡潔に表現できることを見ます。
　この記事ではまず古典エラー訂正符号について概観したあとに、量子エラー訂正符号の基礎を説明し、最後にホモロジーによるCSS符号の記述を扱います。この記事を読むに当たっての前提知識は初歩的な線形代数や量子力学に限りましたが、分量の関係で、古典、量子のエラー訂正符号やホモロジーは簡単な説明にとどまっているため、適宜参考文献を参照していただきたいと思います。
　（内容を詰め込みすぎてしまった感はありますが、ご了承ください...）

1. 古典エラー訂正符号

　まずは古典コンピューターでのエラー訂正符号についてざっくりみていきましょう。ここから先、足し算や掛け算は全て$\Mod2$で考えます。

1-1. 線形符号

　$1$ビットの数$0$と$1$を、$3$ビットに広げて$000$と$111$にしてみます。このとき、もし$3$番目のビットにエラーが入って$001$と$110$となってしまっても、$3$ビットで多数決を取って多い方に合わせることで、$000$と$111$に訂正ができます。エラーが起きる確率が十分小さければ、$2$箇所以上にエラーが起きる確率はおよそエラー確率の$2$乗と十分小さくなるため、情報が壊れてしまうのを抑制できます。このように、ビットの数を増やしてエラーに耐性を付けることを符号化といいます。一般に、$k$ビットの数$x$を$n$ビットの数$f(x)$に符号化するものを$[n,k]$符号と呼びます。特に$f(x)$として線型写像、つまりは行列を考えたものを線形符号と呼びます。
　$0$または$1$が$k$個並んだビット列は、数学的には$\{0,1\}^k=\ff_2^k$というベクトル空間となります。ここで$\mathbb{F}_2\coloneqq\{0,1\}$は単なる$0$と$1$の集合ですが、数学的には有限体 (finite field) の構造が入るため、慣例から$\ff_2$で表します。$\ff_2^k$の元$x$を$k\times n$行列$G$を用いて$G^\trans x\in\ff_2^n$と符号化したものを線形符号と言います。また、この$G$を生成行列と言います。

　上であげた具体例をもう一度振り返ってみましょう。$0$を$000$、$1$を$111$に符号化するとき、符号空間は$C=\{000,111\}$であり、生成行列は
\begin{equation} G= \begin{pmatrix} 1\\1\\1 \end{pmatrix} \end{equation}
です。このとき
\begin{equation} G^\trans \begin{pmatrix}0\end{pmatrix}= \begin{pmatrix}0\\0\\0\end{pmatrix},\quad G^\trans \begin{pmatrix}1\end{pmatrix}= \begin{pmatrix}1\\1\\1\end{pmatrix},\quad C=\im G^\trans \end{equation}
が成り立ちます。この符号を今後$3$ビット反復符号と呼ぶことにします。
　次に、符号化した後にエラーが入った場合に、エラーを検知する方法を考えてみます。少し唐突ですが、これは以下で定義するパリティ検査行列というものを用いることで統一的に達成されます。

　$H$がフルランクであることから、$\ker H$の次元は$\dim\ker H=n-\rank H=k$となります。また定義から$\im G^\trans\subseteq\ker H$であり、$\dim\im G=k$と$\ker H$の次元と等しいことから、以下の命題が成り立ちます。

　パリティ検査行列をエラーが乗っているかもしれない符号にかけることで、エラーが入ってしまったか、またどこにエラーが入ったのかをある程度特定できます。もし符号$y=G^\trans x$にエラーが入っていない場合は、これに$H$をかけた後のベクトルは、パリティ検査行列の定義から$HG^\trans x=0$となります。一方で、$y'=G^\trans x+e$のようにエラー$e$が入った場合を考えると、$H(G^\trans x+e)=He$と、一般には非ゼロになります。よって、$Hy$を測定して$He=Hy$を$e$について解くことで、エラー$e$を特定することができます。エラーがわかれば、符号に$e$を足し算することで$y+e=G^\trans x$としてエラーが訂正できました。
　しかし、$H$は$(n-k)\times n$行列で一般に正則ではないため、逆行列が存在せず、エラー$e$は一意には定まりません。例えば$3$ビット反復符号の場合は、以下のように$1$番目と$2$番目、$2$番目と$3$番目のビットで多数決をとるような行列がパリティ検査行列になります：
\begin{equation} H = \begin{pmatrix}1&1&0\\0&1&1\end{pmatrix} \end{equation}
このとき、以下のようなエラーは区別できません。
\begin{equation} e= \begin{pmatrix}0\\0\\1\end{pmatrix},\quad e'= \begin{pmatrix}1\\1\\0\end{pmatrix} \end{equation}
さらに困ったことに、生じたエラーは$e$だと決め打ちしたときに実際に入っていたエラーが$e'$であったとすると、必ず誤った符号へ移ってしまいます。今回の場合では、$y+e=(G^\trans x+e')+e=G^\trans(x+1)$が成り立ちます。これは一般に成立してしまい、以下の命題が成り立ちます。

　数学的にはほぼ自明に成り立ちますが、エラー訂正の文脈においては非常に有益な示唆を与えます。そのためにも、まず符号の距離を定義します。

　Hamming距離の定義から$d(y,y')=d(y+y',0)$（$\Mod2$では足し算と引き算が同じ結果を与えることに注意してください）がわかるため、重みを$w(y)=d(y,0)$と定めると、$d_C=\min_{y\in C}w(y)$と表すこともできます。以降、誤解の恐れがない場合は$d_C$の添字の$C$を省略して、符号の距離が$d$の$[n,k]$符号を$[n,k,d]$符号と表します。例として、3ビット反復符号の距離は$d=3$です。
　先ほどの命題2に戻りましょう。$y+e,\,y+e'\in\im G$から、その和$e+e'$も符号空間$\im G$に入ることがわかります。よって、$e+e'$の非ゼロの要素は最小で$d$個であり、$e$と$e'$の距離も最小で$d$です。このとき符号に入ったエラーとして、より重みの小さい（つまり発生確率がより高い）方で推定すると、$\lfloor(d-1)/2\rfloor$個までのエラーを訂正できることがわかります。これはエラー訂正符号を設計する上で一つ大事な点です。またこのとき、エラーの発生する確率を$\epsilon$とすると、エラー訂正で失敗してしまう確率は$\epsilon^{\lfloor(d-1)/2\rfloor}$となり、エラーが生じるオーダーを落とすことができました。
　以上のことは、直感的には以下のように理解できます。各符号は$\ff_2^n$上で距離が$d$以上ずつ離れています。もしエラーが発生して符号空間の外に出てしまった場合は、そこから最も近い符号空間の点へ訂正します。（下図参照。黒丸が符号空間の各点を表す。）
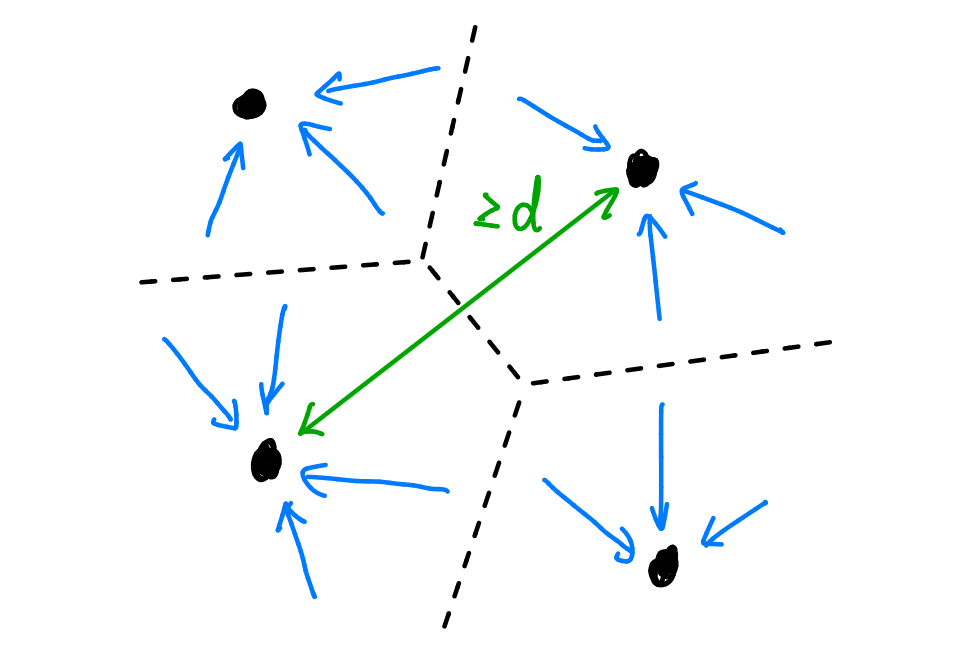エラー訂正のイメージ

1-2. 双対符号

　量子エラー訂正符号へ入る前に、CSS符号で使われる双対符号の導入をします。

　生成行列とパリティ行列を入れ替えたものとなっていて直感的に解釈が難しいかもしれませんが、実は双対符号はもとの符号の直交補空間を成します。（そのため直交補空間を表す記号$\perp$が用いられています。）

　後で補足の部分で用いるため、以下の補題を示しておきます。

1-3. 例：$[7,4,3]$Hamming符号

　この章の最後に、$[7,4,3]$Hamming符号を紹介します。これは後でSteane符号を構成する際に使います。$[7,4,3]$符号のパリティ検査行列の一例は以下です。
\begin{equation} H = \begin{pmatrix} 0 & 1 & 1 & 1 & 1 & 0 & 0\\ 1 & 0 & 1 & 1 & 0 & 1 & 0\\ 1 & 1 & 0 & 1 & 0 & 0 & 1 \end{pmatrix} \end{equation}
これは$H=\left(\begin{array}{c|c}A & I\end{array}\right)$の形をしています。これに対応する生成行列は、一般に$G=\left(\begin{array}{c|c}I & A^\trans\end{array}\right)$として与えられます。
\begin{equation} G = \begin{pmatrix} 1 & 0 & 0 & 0 & 0 & 1 & 1\\ 0 & 1 & 0 & 0 & 1 & 0 & 1\\ 0 & 0 & 1 & 0 & 1 & 1 & 0\\ 0 & 0 & 0 & 1 & 1 & 1 & 1\\ \end{pmatrix} \end{equation}
このとき$HG^\trans=A+A=0$を満たします。

2. 量子エラー訂正符号

　古典符号の準備も済んだところで、いよいよ量子エラー訂正符号の導入に入ります。量子コンピューターはエラーに非常に弱く、保存だけでなく計算をするだけでも、エラー訂正なしではほとんど使い物にならないことが経験的に分かってきています。そのため、量子ビットを全て距離$d$が十分大きな符号空間上に保存し、その上で全ての論理演算を行う必要があります。今回の記事では論理ゲート（符号空間上での操作のこと）の実装方法は詳しく扱いませんが、重要なものについては適宜参考文献を提示したいと思います。
　ここでは初歩的な量子力学の知識は仮定しますが、量子ゲートの記号など、量子コンピューター特有のものは適宜補足します。初歩的な量子力学の教科書としてはshimizu_quant,jj_sakuraiなどが詳しいです。また、量子コンピューター全般やエラー訂正については、nielsen_chuangに詳しく書かれています。
　ここから先、以下のように量子ゲートを略記します。
\begin{gather*} I=\begin{pmatrix}1&0\\0&1\end{pmatrix},\quad X=\begin{pmatrix}0&1\\1&0\end{pmatrix},\quad Y=\begin{pmatrix}0&-i\\i&0\end{pmatrix},\quad Z=\begin{pmatrix}1&0\\0&-1\end{pmatrix}\\ H=\frac{1}{\sqrt2}\begin{pmatrix}1&1\\1&-1\end{pmatrix},\quad S=\begin{pmatrix}1&0\\0&i\end{pmatrix},\quad T=\begin{pmatrix}1&0\\0&e^{i\pi/4}\end{pmatrix},\quad CX=\begin{pmatrix}1&0&0&0\\0&1&0&0\\0&0&0&1\\0&0&1&0\end{pmatrix} \end{gather*}

• $X^2=Y^2=Z^2=I$
• $ZX=-XZ,\quad YZ=-ZY,\quad XY=-YX$
• $XY=iZ,\quad YZ=iX,\quad ZX=iY$

　$H$ゲートは$X$ゲートと$Z$ゲートを入れ替えます（$HX=ZH$）。また、$Z$ゲートの固有値$+1,\,-1$の固有ベクトルをそれぞれ$\ket0,\,\ket1$とし、$X$ゲートに対しても同様に$\ket+,\,\ket-$と表します。$H$ゲートの特性から$\ket+=H\ket0$などが成り立ちます。

2-1. 物理量子ビットと論理量子ビット

　量子ビットとして実際にあるものを物理量子ビット(physical qubit)というのに対し、エラー訂正能力のある、符号化されたビットのことを論理量子ビット(logical qubit)と言います。量子ビットが$n$個あるとき、量子ビット全体で$2^n$次元のヒルベルト空間$\mathcal{H}_n$を張り、論理ビットの張る符号空間はその$2^k$次元の部分空間となります。符号空間が与えられたとき、任意に$k$個の$2$次元空間の直積として分解することで、それぞれの基底として論理ビット$\Ket{\bar0},\,\Ket{\bar1}$を定めることができます。この基底を元に、論理$Z$ゲート、$X$ゲートは
\begin{equation} \bar Z = \Ketbra{\bar0}-\Ketbra{\bar1},\quad \bar X = \KetBra{\bar0}{\bar1}+\KetBra{\bar1}{\bar0} \end{equation}
と構成できます。他の論理ゲートなどについても同様です。
　古典符号と同様に、$n$量子ビットに$k$量子ビットが符号化されている距離$d$の符号を、$[[n,k,d]]$符号と呼びます。符号の距離は、異なる二つの論理状態を移り合うのに必要なゲート数の最小値として定めます。

2-2. 例

　具体例を通して、量子エラー訂正符号を成立させるのに必要な条件を考えてみます。

３量子ビット符号

　古典符号で一番最初に考えた3ビット反復符号をここでも考えてみましょう。古典符号と同じように、以下のように符号化することを考えます。
\begin{equation} \ket0\mapsto\ket{000}=\Ket{\bar0},\ \ket1\mapsto\ket{111}=\Ket{\bar1} \end{equation}
この場合、古典と同じようなビット反転エラー（$X$エラー）は、$\ket{x}$に対して$Hx$に対応するものを測定し、その値に応じて$\ket{x}$のいくつかのビットを反転させることで訂正できます。状態が$\ket0$か$\ket1$を判断するには$Z$演算子で測定すれば良いのでした。$Hx$を知るためには、$Z_1Z_2$と$Z_2Z_3$を測定して、結果$1$なら$0$、$-1$なら$1$と解釈してベクトルの形に並べると、ちょうど$Hx$に対応していることが確認できます。
　ここで、少し気をつけなければならないことがあります。一般に、適当に量子状態を測定してしまうと、量子状態が測定結果に対応する固有空間に射影され、壊れてしまいかねません。例えば、この符号における論理$+$状態$\Ket{\bar+}=(\ket{000}+\ket{111})/\sqrt3$について、一番目と二番目のビットを同時に$Z$で測定し、その積を$Z_1Z_2$の測定結果としてしまうと、測定後の状態は$\ket{000}$または$\ket{111}$となり、エンタングルが壊れてしまいます。
　これを回避するためには、Hadamard testと呼ばれる手法がよく使われます。$U$は固有値$\pm1$の演算子で、複数量子ビットにまたがっても良いとします。このとき、以下のようにすることで、量子状態$\ket\psi$を$U$について測定できます。測定後の状態は、測定結果$s$の固有空間に射影されます。ここで、塗りつぶされた小さい丸は、量子ビットが$\ket1$のときのみ$U$ゲートが作用することを表します（これを制御$U$ゲート、または$CU$ゲートと表記することにします）。

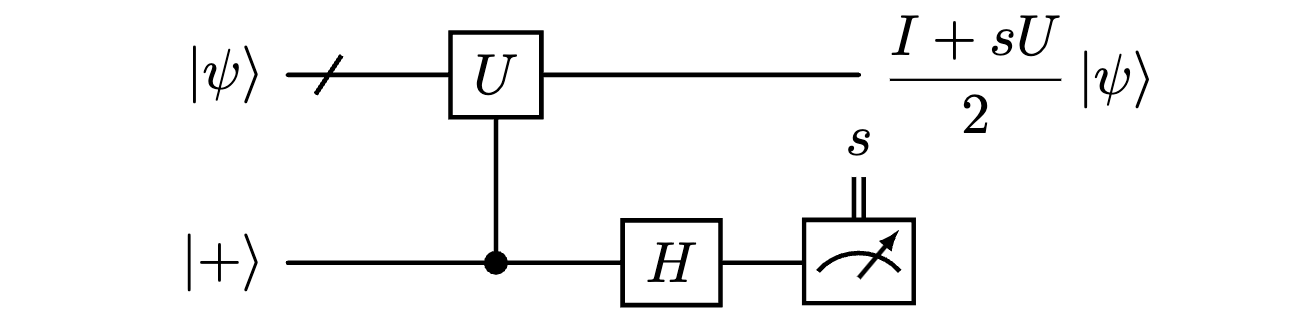Hadamard test

　以上から$X$エラーは訂正できることがわかりました。しかし、量子ビットに発生しうるエラーは他にもあります。例えば、位相が反転するエラー（$Z$エラー）はどうでしょうか。実は、この符号では$Z$エラーは訂正できません。例えば、もし2番目のビットに$Z$ゲートがかかってしまって$\ket1$の位相が反転したとしても、$CX$ゲートは元と同じようにかかり、ancillaは$0$のままとなります。そのため、この回路では$Z$エラーを検知できません。
　一方で、以下のようにエンコードすると、今度は$X$エラーは検知できないものの、$Z$エラーを検知できる符号ができます。
\begin{equation} \ket0\mapsto\ket{+++},\ \ket1\mapsto\ket{---} \end{equation}
どこかのビットに$Z$がかかると$+$と$-$がひっくり返るため、$\ket0\leftrightarrow\ket+$、$\ket1\leftrightarrow\ket-$、$X\leftrightarrow Z$のように対応させて上の議論をそっくりそのまま繰り返すことで、$Z$エラーは検知できることがわかります。
　では、$X$エラーも$Z$エラーも検知できるような符号はどのようなものでしょうか？その一例が次のShor符号です。

9量子ビット符号（Shor符号）

　９量子ビット符号（Shor符号）では、$X$エラー用、$Z$エラー用の二つの３量子ビット符号を組み合わせて、どっちのエラーも訂正できるようにします。具体的には、以下のように論理状態を定義します。
\begin{align} \Ket{\bar0} & =  \Ket{\tilde{+}\tilde{+}\tilde{+}} = \frac{1}{\sqrt2^3}\left(\Ket{\tilde0} + \Ket{\tilde1}\right)^{\otimes3}\\ \Ket{\bar1} & =  \Ket{\tilde{-}\tilde{-}\tilde{-}} = \frac{1}{\sqrt2^3}\left(\Ket{\tilde0} - \Ket{\tilde1}\right)^{\otimes3} \end{align}
ここで$\Ket{\tilde{0}}=\ket{000}$は３量子ビット反復符号です。$ \Ket{\tilde{+}\tilde{+}\tilde{+}}$は３量子ビット符号の上でもう一つの３量子ビット符号を考えていることに対応しています。 $X$エラーは、３量子ビット符号で考えたことを$1\sim3,\,4\sim6,\,7\sim9$番目の量子ビットのそれぞれで考えることで訂正することができます。$Z$エラーは、$1\sim3,\,4\sim6,\,7\sim9$番目の量子ビットをそれぞれ$1,2,3$番目の量子ビットとしてみなしてしまい、その上でエラー訂正を行います。具体的には、$X_1X_2X_3X_4X_5X_6$と$X_4X_5X_6X_7X_8X_9$について測定することで、エラーの情報を得ることができます。このとき、例えば$X_1X_2X_3X_4X_5X_6$の測定値のみが$-1$であった場合、$1,2,3$番目のどの量子ビットに$Z$エラーが入ったのかを特定する必要はないことに注意してください。この３つのどのビットに$Z$エラーが入っても状態は$\Ket{\tilde+}\mapsto\Ket{\tilde-}$のように変わるため、訂正する際も、どれか一つのビットに$Z$をかけるだけで良いです。
　ここまでで$X$エラー、$Z$エラーの２つについては訂正できることがわかりましたが、他のエラーは訂正できるのでしょうか？実は、任意のビット数にまたがるパウリエラーを訂正できれば、理論上は任意のエラーを訂正できることが知られています。これは、一般の時間発展を記述するクラウス演算子がパウリ演算子で展開できるためです。一般の証明はnielsen_chuangなどを参照していただいて、ここでは$1$ビットエラーの場合だけを簡単にみます。（ここでのみ、密度演算子とクラウス演算子を用います。）

　１ビットに生じる任意のエラーはクラウス演算子$\{K_i\}$を用いて、$\rho\mapsto \sum_i K_i^\dagger\rho K_i$と書くことができます。任意の１量子ビットにかかるエラーは$2\times2$の複素行列であるため、複素定数$e_{i,j}$とパウリ行列を用いて
\begin{equation} K_i = e_{i,0}I + e_{i,1}X + e_{i,2}Z + e_{i,3}XZ \end{equation}
と展開できます。このとき$\sum_i K_i^\dagger\rho K_i$も元の状態とパウリエラーが入った項だけが生じます。非対角項は測定で消すことができ、対角項のうちエラーが含まれる項は、$X$エラー、$Z$エラー、またはその両方の項だけであるため、$X$エラーと$Z$エラーの訂正だけで、エラー訂正可能です。
　この符号は$1,4,7$番目のビットに$Z$エラーが入ることで論理状態が変わってしまい、２箇所以内のエラーであれば他の論理状態に変わることはないため、符号距離は３です。よってShor符号は$[[9,1,3]]$符号です。エラー訂正可能であることを保証できるのは、$\lfloor(d-1)/2\rfloor=1$個のエラーまでです。これで量子エラー訂正可能な符号を一つ得ることができました。
　ここでは不完全な二つの量子エラー訂正符号を組み合わせることでエラー訂正符号を得ていました。しかし、得られた符号を見てみると、$X$と$Z$に対してあまり対称的ではないように思えます。対称性が高いほうが一般的には効率が良さそうなので、他により効率の良い符号があるのでしょうか。
　先に答えてしまうと、実は$X$と$Z$について分けたような符号（CSS符号）の枠組みでは$[7,1,3]$符号（Steane符号)が、CSS符号に限らなければ$[[5,1,3]]$符号が知られていますperfect。次からは、そのような様々な符号を得るための枠組みを見ていきます。

2-3. stabilizer

　量子計算において、論理ビットの空間はヒルベルト空間の部分空間として規定されます。この空間をstabilizerと呼ばれる演算子たちの固有値$+1$の同時固有空間として定義すると、stabilizerを測定することでエラーの入ったビットを特定できるようになります。例えば、$3$量子ビット反復符号のstabilizerの張る空間は
\begin{equation} \mathcal{S} = \{I,\,Z_1Z_2,\,Z_2Z_3,\,Z_3Z_1\} \end{equation}
となります。これらの固有値$1$の同時固有空間は$\span\{\ket{000},\ket{111}\}$であることはすぐに確認できると思います。量子ビットにエラーが入り符号空間から外れてしまう（例えば$\ket{010}$）と、いくつかの$S$の元（$Z_1Z_2,Z_2Z_3$）による固有値が$-1$となり、測定で検知することができます。またこのことは、エラー$X_2$がstabilizer$Z_1Z_2$と反交換すること$Z_1Z_2X_2=-X_2Z_1Z_2$から、$X_2\ket{000}$が$Z_1Z_2$の$-1$の固有状態となっていることとして確認できます。
　一般のエラーを訂正するには$X$エラーと$Z$エラーを訂正できれば十分であることから、stabilizerとしては$X$や$Z$の積、あるいは同じことですが、パウリ行列の積を考えることにします。
　パウリ行列の集合をとその積で閉じるように拡張した群
\begin{align} \mathcal{P}_1 &= \{\pm I,\pm iI,\pm X,\pm iX,\pm Y,\pm iY,\pm Z,\pm iZ\}\\ &= \{\pm1\pm i\}\times\{I,X,Y,Z\} \end{align}
を$1$次元のパウリ群と呼びます。パウリ行列の$n$個までのテンソル積からなる群
\begin{align} \mathcal{P}_n &= \{\pm1\pm i\}\times\left\{\bigotimes_{k=1}^n P_k\ \middle|\ P_k\in\{I,X,Y,Z\}\right\}\\ &= \{\pm1\pm i\}\times\{I,X,Y,Z\}^{\otimes n} \end{align}
を$n$次元のパウリ群と呼びます。この部分群としてstabilizer群を定義します。ここで、符号空間は各stabilizerの$+1$の同時固有状態としたいので、$-I$は除きます。

　$-I\notin\mathcal S$と$\mathcal{S}$が行列積について閉じていることから$\pm iI\notin\mathcal{S}$が言えます。また一般にパウリ群の任意の元$g$の二乗は$\pm I$となりますが、このうち$g^2=I$となるもののみがstabilizerとなり得ます。これより、$g$と$-g$や$\pm ig$が同時にstabilizerにはならないことが言えます。さらに、$g,g'\in\mathcal{S}$はそれぞれパウリ行列の積なため、交換または反交換しますが、反交換$gg'=-g'g$とすると$(gg')(-g'g)=-I\in\mathcal{S}$となり定義と矛盾します。よって互いに交換するもののみがstabilizer群に含まれるため、全ての$\mathcal{S}$の元の同時固有状態が存在します。整理すると、以下のようになります。

　このようにして定義されたstabilier群に対し、その元の固有値$+1$の同時固有空間を符号空間とする符号をstabilizer符号と言います。stabilizerによりヒルベルト空間の自由度は$m$個だけ減るため、stabilizer符号は$[[n,n-m]]=[[n,k]]$符号です。（以降$m=n-k$の関係があるとします。）stabilizerはエラーの検出の方法が与えられていることから、理論としてエラー訂正が非常に簡単になります。そのため、多くの量子エラー訂正符号はstabilizer符号です。（後で紹介するCSS符号や表面符号、Shor符号、Steane符号は全てstabilizer符号です。）
　群論の一般論から、stabilizer群はいくつかの独立なstabilizer（生成元）で
\begin{equation} \mathcal{S} = \langle g_1,g_2,\dots,g_m\rangle \coloneqq \left\{g_1^{i_1}g_2^{i_2}\cdots g_m^{i_m}\ \middle|\ g_j\in\mathcal{S},\ \vec{i}\in\{0,1\}^{\otimes m}\right\} \end{equation}
と表すことができます。$3$量子ビット反復符号なら$\mathcal{S}=\langle Z_1Z_2,Z_2Z_3\rangle$です。一般に生成元はパウリ行列のテンソル積であるため、係数を除いて$X,Z$の指数のみで表すことができます。これを全ての生成行列について並べたものを検査行列と言います。

検査行列

　検査行列（またはstabilizer）は古典線形符号のパリティ検査行列に対応する概念です。（このことはCSS符号の場合について後で詳しく見ます。）

　stabilizer群には$g$と$-g$などは同時には存在できなかったため（補題5）、$H$の行は全て異なります。また生成群は互いに独立であることから$H$の各行は線型独立であることが言え、$H$はフルランクであることがわかります。
　stabilizer群の性質のうち任意の二つのstabilizerが交換することは、検査行列を使うと簡潔に表すことができます。

stabilizer符号の論理$X,Z$ゲート

　stabilizerが定まると、そこから一般に論理$X,Z$ゲートを構成することができます。論理ゲートであるためには、全てのstabilizerと可換で符号空間を壊さないことが必要です。これは論理$Z$ゲートを$\bar{Z}_1,\bar{Z}_2,\dots,\bar{Z}_k$として、$\langle g_1,\dots,g_{n-k},\bar{Z}_1,\dots,\bar{Z}_k\rangle$がstabilizerとなることが条件です。このような$\bar{Z}_1,\dots,\bar{Z}_k$を取ってくることができれば、$x_i\in\{0,1\}$として$\big\langle g_1,\dots,g_{n-k},(-1)^{x_1}\bar{Z}_1,(-1)^{x_2}\bar{Z}_2,\dots,(-1)^{x_k}\bar{Z}_k\big\rangle$でstabilizeされる状態が、論理ビット$\Ket{\overline{x_1\dots x_k}}$に対応します。また、論理$X$ゲートは、各$\Ket{\overline{x_i}}$を$\Ket{\overline{1-x_i}}$に移し、かつその他の論理ゲート、stabilizerと可換になるものとして構成できます。このような論理ゲートが本当に存在するかは少し非自明ですが、検査行列$H$に行基本変形を繰り返して標準形にすることで、具体的に構成することができます。（nielsen_chuang §10.5.7）

2-4. CSS符号

　ここでは、stabilizerが$X$と$Z$の二つに分かれている符号として、CSS符号を紹介します。CSS符号がこの記事の目玉となる符号です。stabilizer符号よりは一般性が下がるものの、あとで紹介するSteane符号や表面符号を含みます。

　この定義がwell-definedであることは、任意の$x'\in[x]$は$x'=x+y'\ (y'\in C_X^\perp)$と書けて、
\begin{equation} \ket{x'+C_X^\perp} = \sum_{y\in C_X^\perp} \ket{x+y'+y} = \sum_{y'+y\in C_X^\perp} \ket{x+y'+y} = \ket{x+C_X^\perp} \end{equation}
が成り立つことから分かります。この話からも分かるように、CSS符号は$C_Z$から$C_X^\perp$に相当する自由度を潰したものになっています。符号空間の次元について考えると、$C_X$が$[n,k_X]$符号、$C_Z$が$[n,k_Z]$符号であるとき、$C_Z/C_X^\perp$の次元は$k_Z-(n-k_X)=k_X+k_Z-n$なので、$\text{CSS}(C_X,C_Z)$は$[[n,k_X+k_Z-n]]$符号です。
　CSS符号は以下の性質を持ちます。

CSS符号の論理ゲート

　 一般のstabilizer符号では、論理$X,Z$ゲートがそれぞれ物理$X,Z$ゲートのみからなるとは限りません。一方で、CSS符号は検査行列が$X$について、$Z$についてでブロック対角型の構造をしているため、論理$X$ゲートは物理$X$ゲート、論理$Z$ゲートは物理$Z$ゲートのみから構成できます。例えば論理$Z$ゲートは、$\bar{Z}=Z^{g}=Z^{g_1}\dots Z^{g_n}$として$X$stabilizerと交換するもの（$g\in\ker H_X$）のうち、$Z$stabilizerを含まないもの（$\row H_Z=\im H_Z^\trans$の成分を除く）として得られます。すなわち、
\begin{equation} g\in\ker H_Z/\im H_X^\trans \end{equation}
が論理$Z$ゲートに対応します。同様に、論理$X$ゲート全体の集合は$\ker H_X/\im H_Z^\trans$として得られます。

7量子ビット符号（Steane符号）

　古典線形符号$C_X,C_Z$として共に$[7,4,3]$Hamming符号$C$を取ったものを考えます。CSS符号の条件$C_X^\perp\subseteq C_Z$は命題7の証明中の議論より$H_ZH_X^\trans=0$、すなわち$HH^\trans=0$となります。$[7,4,3]$Hamming符号の場合で計算してみると、
\begin{equation} HH^\trans = \begin{pmatrix} 0 & 1 & 1 & 1 & 1 & 0 & 0\\ 1 & 0 & 1 & 1 & 0 & 1 & 0\\ 1 & 1 & 0 & 1 & 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} 0 & 1 & 1\\ 1 & 0 & 1\\ 1 & 1 & 0\\ 1 & 1 & 1\\ 1 & 0 & 0\\ 0 & 1 & 0\\ 0 & 0 & 1 \end{pmatrix} = \begin{pmatrix} 0 & 0 & 0\\ 0 & 0 & 0\\ 0 & 0 & 0 \end{pmatrix} \end{equation}
のように、成り立つことがわかります。このようにして得られた$\text{CSS}(C,C)$符号を7量子ビット符号、またはSteane符号と言います。これは$[[7,1,3]]$符号です。
　Steane符号の独立なstabilizerは以下の６つです。これらは$H_X,H_Z$の行から得られます。
\begin{align} g_1 &= X_2X_3X_4X_5 & g_2 &= X_1X_3X_4X_6 & g_3 &= X_1X_2X_4X_7\\ g_4 &= Z_2Z_3Z_4Z_5 & g_5 &= Z_1Z_3Z_4Z_6 & g_6 &= Z_1Z_2Z_4Z_7 \end{align}
Steane符号はstabilizerが$X$と$Z$で同じ構造を持っていることが特徴の一つです。論理$X,Z$ゲートはこれらと独立かつ互いに反可換なものとして
\begin{equation} \bar{X} = X_1X_2X_3X_4X_5X_6X_7,\quad \bar{Z} = Z_1Z_2Z_3Z_4Z_5Z_6Z_7 \end{equation}
と得られます。$k=1$なので一つだけで十分です。$\bar{X}g_1=X_1X_6X_7$などを論理$X$ゲートとして採用することもできます。Steane符号は$C_X$と$C_Z$が同一なため、stabilizerと論理演算子はともに$X$と$Z$の入れ替えについて対称な形に撮ることができます。このとき、全ての物理ビットに$H$や$CX$をかけることで、全ての論理ビットに同時に$H$や$CX$をかけることができます。（$CX$は二つ同じ符号を持ってきて、対応する物理ビット同士に同時に$CX$をかけます。）$k>1$の場合に一つの論理ビットだけに選択的に$H$をかけるのはこれだけでは難しいですが、全てに作用させるだけであれば簡単にできるのが嬉しい点です。

2-5. toric codeと表面符号（surface code）

　量子エラー訂正符号の導入として、最後にtoric codeと表面符号（surface code)の紹介をします。toric codeはKitaevによって導入されましたkitaev。そこから周期的境界条件を除いたものが表面符号です。
　toric codeはハミルトニアンが以下で与えられるようなスピン模型でもあります。
\begin{equation} \mathcal{H} = -\sum_s X_s - \sum_p Z_p \end{equation}
$X_s$は頂点演算子(star operator)、$Z_p$は面演算子(plaquette operator)と呼ばれているもので、それぞれ対応する頂点や面の周辺の物理量子ビットに$X$または$Z$をかける演算子です。

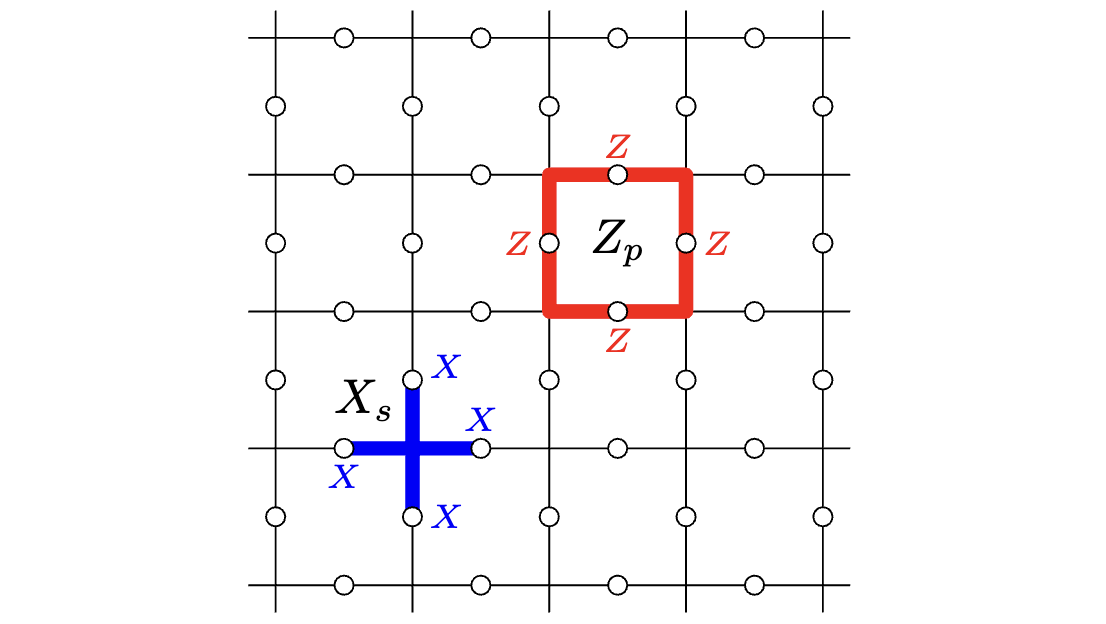toric code

頂点演算子と面演算子の交わる量子ビット数は$0$または$2$なので、これらは全て可換です。よって、これをstabilizerとするstabilizer符号を考えることができます。またstabilizerが$X$ごと、$Z$ごとに分かれているため、$CSS$符号でもあります。
　スタビライザー測定は、例えばそれぞれ頂点と面の中心部分に測定用の補助ビットを追加し、Hadamard testを行います。論理ゲートは、以下の図5のように縦方向や横方向に一周$X$や$Z$をかけることで得られます。論理$X$ゲートは$Z$stabilizerと偶数回だけ交わり、論理$Z$ゲートは$X$stabilizerと偶数回だけ交わるため、これらの論理ゲートはstabilizerと交換することがわかります。論理$X,Z$がそれぞれ二つずつ取れるため、toric codeでは一つの符号あたり2ビット埋め込めます。
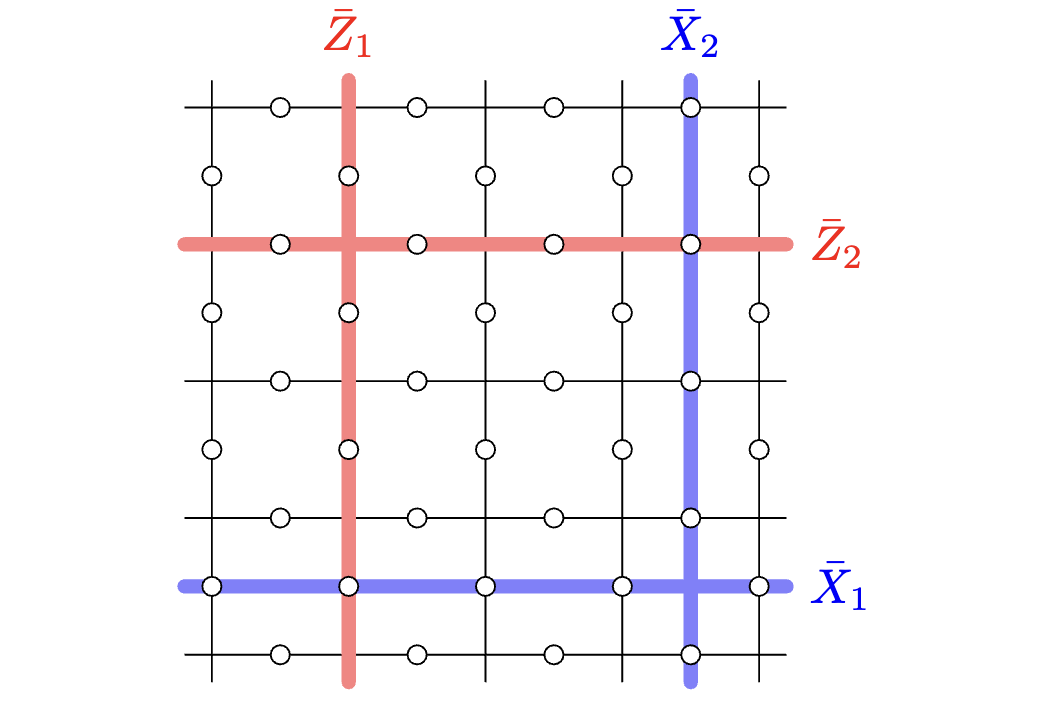toric codeの論理ゲート
　toric codeは周期境界条件のために、２次元トーラス上に定義された符号と見ることができます。一方で表面符号は周期境界条件は取らないため、stabilizerは全て局所的な演算子となっています。また、周期的境界条件を外したことで、論理ビットは一つになります。（これは物理ビットの数とstabilizerの数の差が$k=1$になることから確かめることができます。）

表面符号の実装

　複数ビットを埋め込み、他の論理ゲートを実装するためには大きく二つの方法が考えられています。一つ目はstabilizerひとつをオフにして（stabilizer測定をしないようにして）、符号に穴を開ける方法です。
　一般に、表面符号上の"可縮な"ループはstabilizerの積となり、論理状態を変えません。例えば以下の図の左辺のように、$Z$ゲートをループ状にかけることを考えます。$Z$stabilizerは面の周囲４ビットの$Z$ゲートの積でした。stabilizerは論理状態を変えないため、論理恒等演算子と見ることができます。これを順にかけていくと、最後は$Z$stabilizerだけが残り、恒等演算子として作用します。
可縮な$Z$ゲートのループ
　論理状態に非自明に作用するのは非可縮なループだけとなり論理ビットに対応します。その数は種数（穴の数のようなもの。トーラスでは$1$）のちょうど２倍です。よって、符号の表面に穴を開けていくことで、論理ビットを増やしていくことができます。その他の論理ゲートなどはsurfaceにまとめられています。
　もう一つの実装方法として、lattice surgeryと呼ばれる手法を用いて論理ゲートを構成する方法がありますlattice。これを使うと、複数の格子を"縫い合わせ"たり二つに分けたりすることができるため、一つの大きな符号にたくさんの量子ビットを埋め込む必要がなくなります。これにより、必要な量子ビット数を定数倍だけ落とすことができます。
　表面符号の特徴として、エラー訂正から論理演算までの全てをlocalに実装できることが挙げられます。エラー訂正符号をハードウェアに実装するにあたり、この特性は非常に大事です。特に超伝導量子ビットでは物理的に量子ビットを動かすことが難しいため、局所的な操作で閉じるような符号として、表面符号はメジャーな符号となっています。
　一方で、中性原子型の量子コンピューターなどでは量子ビットを直接動かすことができるため、局所的な演算だけは閉じていないエラー訂正符号も近年は注目されています。

3. ホモロジーの紹介

　位相幾何学において、ホモロジーとは位相空間の持つ特性を代数的な視点で解析する方法です。ここでは簡単な定義と例のみを扱います。物理屋さんに向けて書かれた本としては、nakatopoが有名です。

　なんだかややこしいですね。今回はエラー訂正にのみ興味があるので、$R$として$\ff_2$、鎖複体としてベクトル空間$C_n=\ff_2^{k_n}\ (k_n\in\intset)$と線型写像$\del_n\colon C_n\to C_{n-1}$だけを考えることにします。
　境界作用素は$\del_n\circ\del_{n-1}=0$を満たすように取ります。境界作用素で2回送ると0に移るということなので、境界作用素で一回送ったものは隣の境界作用素の核に入ります。つまり、$\im\del_{n-1}\subseteq\ker\del_n$が成り立ちます。よってこの間に商ベクトル空間を定義することができます。これをホモロジー群と呼びます。

　位相幾何学では、このホモロジー群から$R$-加群の台となる位相空間の性質がわかるため、現代数学の非常に強力な武器の一つとなっています。
　鎖複体を考えたときは境界作用素が添字を減らす方向に作用していましたが($C_n\to C_{n-1}$)、逆に添字を増やすようにとったものを余鎖複体(cochain complex)といいます。これに対応して、境界作用素はコバウンダリ作用素(coboundary operator)、ホモロジー群はコホモロジー群といいます。鎖複体とは番号を増やすか減らすかの違いしかなく、ほとんど同じように思えますが、実際二つの間には同型が存在していて、大きな違いはありません。ある鎖複体に対して、それを鎖複体と呼ぶか余鎖複体と呼ぶかは慣習によるところが大きいようです。数学的には、各$C_n$をその双対空間$C_n^*$で、境界作用素をその転置$\partial_n^\trans$で置き換えたものに相当します。
　抽象的な話は多かったので、いくつか例をあげたいと思います。とはいっても構成が複雑な分、例も複雑になってしまうので、ここではお気持ちだけにして、詳しくは他の文献を参照していただきたいと思います。

例1：単体的ホモロジー群

　$d$次元の凸図形の構成要素ようなものを単体と呼びます。例えば$\mathbb{R}^n$において、0次元単体は点、1次元単体は線、2次元単体は三角形、3次元単体は四面体です。正確には、$d+1$個のベクトル$\vb*a_0,\,\dots\vb*a_d$を、これらが指し示す点の全てが$d-1$次元以下の$\mathbb{R}^n$の部分空間に入っていることはないとして、集合
\begin{equation} \left\{\sum_{i=0}^d\lambda_i\vb* a_i\in\realset^n\middle|\lambda_i\in\realset_{\ge0},\ \sum_{i=0}^d\lambda_i=1,\ \right\} \end{equation}
の元を単体と呼びます。この単体を、同じ次元の面同士で貼り合わせてできる図形を単体複体と呼びます。（同じ次元とは、例えば頂点同士、辺同士で貼り合わせることは許すが、頂点と辺をくっつけることは許さない、ということです。）単体や複体は一般の(位相)空間でも考えることができて、$n$次元の単体複体全体から生成される自由加群を$C_n$とします（整数などを係数として、形式的に単体複体の線形和をとったようなものです）。境界作用素は、そのままの意味で「境界」をとってくるような作用素として定義します。一般にこのような図形の境界を考えると一つ次元が下がった図形になると思います。また、これは少し直感的ではないかもしれませんが、一般に図形の境界には境界が存在せず、閉集合になっています。そのため、このようにして構成した$C_n$と境界作用素は鎖複体を成します（単体的鎖複体）。
　このとき得られるホモロジー群$\ker \del_n/\im\del_{n+1}$は、元となった空間の$n$次元の"穴"の数に対応します。（ここでの"穴"の数は、種数とはまた別のものです。）

例2：微分形式

　ここでは簡潔に紹介するだけとします。微分形式に詳しくない方は、読み飛ばしていただいて大丈夫です。
　$M$を可微分多様体、$\Omega^0(M)$を$M$上の滑らかな関数全体、$\Omega^n$を$M$上の$n$次微分形式とします。また、外微分を$d^n\mathpunct:\Omega^n\to\Omega^{n+1}$で表します。外微分は$d^n\circ d^{n+1}$を満たすため、以下のような(余)鎖複体が構成できます。
\begin{equation} \Omega_0\xrightarrow{d_0}\Omega^1(M)\xrightarrow{d_1}\Omega^2(M)\xrightarrow{d_2}\cdots\xrightarrow{d_{n-1}}\Omega^n(M)\xrightarrow{d_n}\cdots \end{equation}
ここから得られるコホモロジーはド・ラームコホモロジーと言い、単体的ホモロジーと同様に、多様体$M$の"穴"の数のような幾何的な構造を特徴付けます。

4. CSS符号のホモロジーによる記述

　$\text{CSS}$符号$\text{CSS}(C_X,C_Z)$は以下のように定義することができます。まず、符号検査行列$H_Z$と$H_X$を選んできます。対応する古典符号空間は$\ker H_Z$と$\ker H_X$です。$Q_2,\,Q_1,\,Q_0$をそれぞれ$Z$-check、物理量子ビット、$X$-checkとして、以下のような鎖複体（余鎖複体）として$\text{CSS}$符号を定義することができます。
\begin{gather} Q_2\xrightarrow{H_Z^\trans}Q_1\xrightarrow{H_X}Q_0\\\\ \left(Q_0\xrightarrow{H_X^\trans}Q_1\xrightarrow{H_Z}Q_2\right) \end{gather}
この鎖複体と余鎖複体は双対関係にあるため、どちらで定義しても同じです。論理$Z$ゲートと論理$X$ゲート全体からなる集合は、それぞれホモロジー群とコホモロジー群
\begin{equation} \vb*{\bar{Z}} = \ker H_X/\im H_Z^\trans,\quad \vb*{\bar{X}} = \ker H_Z/\im H_X^\trans \end{equation}
として与えられます。表面符号のような大きな符号では全ての論理状態を書き下すのはあまり現実的ではなかった一方で、鎖複体とホモロジー群で記述することにより、stabilizerと論理演算子だけしか見る必要がなくなり、状態を直接扱わずに済むことになります。
　上の定義では少し抽象的なため、具体的に見てみましょう。大事な見方として、演算子は指数部分に注目し、$\ff_2$上で考えます。例えば、$n=6$量子ビットのヒルベルト空間の演算子$Z_1Z_3Z_4Z_5$は、
\begin{equation} Z^{h} = Z_1^{h_1}Z_2^{h_2}Z_3^{h_3}Z_4^{h_4}Z_5^{h_5}Z_6^{h_6} \end{equation}
として、$h=(1,0,1,1,1,0)$で表します。
　$Q_2,Q_1,Q_2$は、それぞれ$\ff_2^k,\,\ff_2^n,\,\ff_2^k$と同型となります。$Z$check$Q_2$は、例えば$h=(0,1,1,1,0,0)^\trans\in\ff_2^k\cong Q_2$に対して、$H_Z^\trans h$は$2,3,4$番目の$Z$stabilizerの積を表しています。$\ff_2^n\cong Q_1$の元は、複数の量子ビットそのもの、またはそこにかかる何らかの演算子の指数部分を同一視したものです。$X$check$Q_0$は、$h\in\ff_2^k\cong Q_0$をコバウンダリ$H_X^\trans$で送った先$h'=H_X^\trans h$が、$h'_i$が$1$であるような$i$番目のstabilizerの積を表します。
　CSS符号の条件$C_X^\perp\subseteq C_Z$は$H_ZH_X^\trans=0$と同値であり、これはコバウンダリを２回作用させると$0$になる条件と等価です。
　CSS符号の論理演算子がそれぞれ$\vb*{\bar{Z}} = \ker H_X/\im H_Z^\trans,\quad,\ \vb*{\bar{X}} = \ker H_Z/\im H_X^\trans$で表せられることは、$2$章で少し触れました。論理Xゲートは、$Z$stabilizerと可換なもの$\ker H_Z$のうち、$Z$stablizerの成分を除いたもの$/\im H_X^\trans$として得られます。これを符号空間を使って表すと、$C_Z/C_X^\trans$となり、CSS符号の論理ビットと同型になっています。論理$Z$ゲートは$C_X/C_Z^\trans$であり、これもCSS符号の論理ビットと同型です（$2$章の補足も参照）。

表面符号再考

　最後に、表面符号をホモロジーの観点から眺めてみましょう。表面符号では、$X$stabilierは頂点、$Z$stabilizerは面に対応していました。また、量子ビットは辺に対応しています。ここで、単体的ホモロジー群と同じように、面、辺、頂点から生成される加群を$C_2,C_1,C_0$として、$\del_n$をその境界作用素とします。このとき、$\del_2$は$Z$stabilizerの周りの量子ビット、$\del_1^\trans$は$X$stabilizerの周りの量子ビットをとってくる演算子となっているため、$C_2\xrightarrow{\del_2}C_1\xrightarrow{\del_1}C_0$は$Q_2\xrightarrow{H_Z^\trans}Q_1\xrightarrow{H_X}Q_0$と同型になります。また、論理ゲートはホモロジーで与えられていましたが、それらは$\ker\del_1/\im\del_2$やその双対と同型となり、幾何的な構造を反映していることがわかります。
　ここまで考えていた表面符号は全て２次元で考えていましたが、３次元や４次元での表面符号も考えられていますexp_4d。４次元の表面符号では、例えば$C_3\to C_2\to C_1$で鎖複体を作り、残りの$C_4\to C_3,\ C_1\to C_0$はそれぞれ$Z,X$stabilizer測定の古典的なメタチェックとして使用することなどが考えられています。
　以上からわかるように、（幾何的な？）長さ$\ge2$の鎖複体の構造を一つ持ってくると、それに対応するオリジナルなCSS符号を一つ作ることができるのです！

5. おわりに

　少し導入の部分が長くなりすぎてしまったかもしれませんが、楽しんでいただけたでしょうか。個人的には量子エラー訂正符号に位相幾何学が絡んでくるなんて思いもしていなかったので、初めて触れたときはかなり驚いていた覚えがあります。ただ、いざ慣れてみると非常に便利で、論理ビットを計算する必要がないのはありがたいですね。
　この記事ではほとんど触れることができなかったけど興味がある話題として、homological product codehomologicalpartitioningや３次元以上の表面符号exp_4dがあります。また機会があれば書くかもです。

更新履歴

• 2-3節の記述を一部修正しました。全体のレイアウトを一部変更しました。(2025/11/15)