可換環論の†全て†を幾何に翻訳して鑑賞しよう~前編~
この記事は駒場理数豚汁カレンダー9日目の記事です。
ハブ →
駒場理数サークルのHP
Introduction
こんにちは。Mark6 という者です。
あなたは、(可換)環論の勉強中に
 これは何?
これは何?
このような図を描いたことはありますでしょうか。
無いなら、私はこの記事をあなたのために書いたようなものです。
この記事では、可換環論における様々な現象を、位相空間における現象に翻訳し、大量の図を添えて解釈していきます。
純代数的に定義され純代数的な文脈でしか聞いたことがなかった概念が、じつは幾何に翻訳すると親しみやすい生き生きとした手触りを持っていた......なんてことがあったら、それは素敵なことだと思いませんか?
この記事は、
- 代数的整数論などの文脈で環論を勉強したが、その幾何的な側面についてはまだよく知らないという方
あるいは、
- アティマクなどで可換環論を勉強中の方
などを念頭に置いた、代数多様体 (variety) への導入記事です。
- この記事では、環と言ったら単位元を持つ可換環を指します。
なにも言わず用いたら、各文字は以下のものを指すことにします。
$A$:適当な環
$\mfp$:適当な素イデアル
$\mfa$:適当なイデアル
$k$:適当な代数閉体 - 可換環論を学んだことがあるとより楽しめると思いますが、図だけである程度の雰囲気はつかめるよう書いたつもりです。
- 私自身がまだこの分野を勉強中なのに加え、多分にイメージや解釈を含む内容です。数学的な間違いは無いよう気を付けていますが、人によっては解釈違いが大量に発生すると思います。改善案があればぜひ教えてください。直します。
- 記事を短くまとめるために、その場しのぎな定義をしたり、用語をごまかしたりしています。
各節は以下のように進みます。
代数
可換代数側の概念を提示し、定義や命題を列挙します。
幾何
述べた代数的な命題が幾何的にはどのような事実に対応するのかを述べます。
図と例
具体的な環やイデアルで計算し、図を鑑賞します。
Overview
- 環$A$に対し、その素イデアル全体の集合$\Spec(A)$にZariski位相を導入します。これによって環 → 位相空間という対応が定まり、環の各種概念がこの位相空間に反映されていきます。
- 環の例として多項式環を取り、零点定理弱形を用いつつその$\Spec$を図示して鑑賞します。
- 素イデアルが(既約)閉部分多様体に対応すること、極大イデアルは閉点に対応することを観察します。
- 環$A$のイデアル$\mfa$には、その根基と呼ばれるイデアル$\sqrt{\mfa}$が定まります。
- 環の例として再び多項式環を取り、零点定理強形を用いつつ$\mfa$が定める図形と$\sqrt{\mfa}$が定める図形の関係を鑑賞します。
- イデアルの根基がある意味で閉包の対応物と見れることを観察し、根基を取って失われる情報について考察します。
- 素イデアルの一般化である準素イデアルを定義し、良い環においては任意のイデアルを準素イデアルによって分解できることを述べます。
- 多項式環におけるイデアルの準素分解$\mfa=\bigcap\mfq_i$の例をひとつ取り、$\mfa$が定める図形と$\mfq_i$が定める図形の関係を鑑賞します。
- イデアルの準素分解が、図形の既約分解(の弱いバージョン)に対応していることを見ます。
- 整性・整閉性を定義し、整数論的な例を述べます。
- 上昇/下降定理を述べ、それを幾何的に解釈します。
- 整性・整閉性が、$\Spec$においては良い「被覆」を誘導していることを見ます。
この記事(前編)はここまでです。
後編はいつか書きます。以降はただの予定です。
- 環の局所化(単元を付け加える操作)を定義し、その性質をいくつか確認します。
- 多項式環の局所化を計算し、それがまさに「局所的な」関数環と思えることを見ます。
- Zariski 位相の開基が局所化によって解釈でき、よってある種の局所化が開部分多様体に対応することを見ます。
- 付値・付値環を定義し、基本的な事実を確認します。
- 体に対して Zariski-Riemann 空間という位相空間を構成できることを見て、いくつか例を計算します。
- 関数体から、それに入る付値を「点」とみることで曲線を復元できることを見ます。
- 離散付値環を定義し、整数論的な例や性質を列挙します。
- 特異点を持つ曲線に対して各点での局所環を計算し、特異点でのみ離散付値環でないことを確認します。
- Jacobian で定義される「非特異性」が、環の言葉に翻訳するとまさに離散付値環の概念に対応していることを見ます。
- イデアルによる環の完備化を定義し、諸性質を確認します。
- 曲線の局所環を完備化することで、特異点の非常に局所的な様子を代数的に観察できることを計算します。
- 勉強不足でまだよく分かっていないので、勉強次第書きます。
素イデアルと幾何(Zariski位相と零点定理弱形)
環$A$に付随する位相空間$\Spec(A)$を構成します。
代数
環$A$の素イデアル全体の集合を$\Spec(A)$と書く。
$A$のイデアル$\mfa$に対し$$V(\mfa)=\{\mfp\in\Spec(A)\mid\mfa\subseteq\mfp\}$$と定める。つまり$V(\mfa)=\{~\mfa$を含む素イデアル$\}$である。
- $V(A)=\emptyset$
- $V((0))=\Spec(A)$
- $V(\mfa\mfb)=V(\mfa)\cup V(\mfb)$
- $V(\sum\mfa_i)=\bigcap V(\mfa_i)$
幾何
上の命題により、$V(\mfa)$らは$\Spec(A)$における閉集合系の公理を満たしている。
$V(\mfa)$の形をした部分集合を閉集合とする$\Spec(A)$の位相を Zariski 位相という。
以降$\Spec(A)$と書いたら、Zariski 位相を入れた位相空間を指すものとします。
代数
集合として
$$\Spec(A/\mfa)\cong V(\mfa)$$
である、すなわち「$A/\mfa$の素イデアル」と「$A$の素イデアルで$\mfa$を含むもの」には自然に全単射がある。
幾何
$V(\mfa)$に$\Spec(A)$からの相対位相を入れると、上の
$$\Spec(A/\mfa)\cong V(\mfa)$$
は位相を含めた同型である。
代数
環準同型$\varphi:A\to B$があるとき、$B$の素イデアル$\mfq$の$\varphi$による逆像$\varphi\inv(\mfq)$は$A$の素イデアルとなる。$\varphi\inv(\mfq)$を$\mfq$の縮約(contraction)という。
幾何
環準同型$\varphi:A\to B$があるとき、縮約によって$$\varphi^*:\Spec(B)\to\Spec(A);\mfq\mapsto\varphi\inv(\mfq)$$が誘導され、これは Zariski 位相について連続である。
環準同型に対して$\Spec$の連続写像を対応させられる一方で、$\Spec$の間の連続写像のすべてが環準同型から得られるとは限りません。"$\Spec$だけでは情報が足りない"のですね。この問題は一旦深追いせず、例に移りましょう。
図と例
Zariski 位相は非常に"弱い"、つまり開集合の少ない位相であり、図示もかなり難しいです。
例を4つ挙げます。
- 例1:$A=k[x,y]$
スタンダードな2変数多項式環で$\Spec$を図示します。 - 例2:$k[x,y]/\mfp$
素イデアルによる剰余環が、閉部分多様体を与えることを見ます。 - 例3:2種類の$k[x]\to k[x,y]/(x^2-y)$
環準同型が$\Spec$の間に誘導する写像を図示します。 - 例4:$A=k[x_1,\cdots,x_n]$
零点定理弱形を用いて、多変数多項式環の$\Spec$を調べます。
例1:$A=k[x,y]$
$A$の素イデアル、すなわち$\Spec(A)$の点は
- 零イデアル$(0)$
- 既約多項式$f$による$(f)$
- $\alpha,\beta\in k$による極大イデアル$(x-\alpha,y-\beta)$
の3種類です。包含関係を上下関係として図示すると以下のようになります。
![!FORMULA[71][1507781240][0]の素イデアル](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2FgzoFKOC9sNJrewxgCZ7E.png?alt=media) $k[x,y]$の素イデアル
$k[x,y]$の素イデアル
$$(f)\subseteq(x-\alpha,y-\beta)\Leftrightarrow f(\alpha,\beta)=0$$
であることに注意します。
上の図式において、素イデアル$(x-\alpha,y-\beta)$を$k^2$の点$(\alpha,\beta)$と同一視することで、以下のように図示できそうです。
![!FORMULA[76][-361479656][0]の図示](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2FfkmP511Bi9553n8JVWbi.jpg?alt=media) $\Spec(k[x,y])$の図示
$\Spec(k[x,y])$の図示
$\Spec(A)$の上のシートから説明します。
- 一番上のシートは極大イデアル$(x-\alpha,y-\beta)$らを表しています。これらの特徴は閉点であるということです──つまり、$\overline{\{(x-\alpha,y-\beta)\}}=\{(x-\alpha,y-\beta)\}$となっています。閉点全体は$$(x-\alpha,y-\beta)\leftrightarrow(\alpha,\beta)$$という対応によって$k^2$と全単射があります。
- 2枚目のシートには曲線が描いてありますが、$(f)$や$(g)$は$\Spec(A)$においてあくまでひとつの"点"であることに注意しましょう。これらは閉点ではないので、閉包を取ると$$\overline{\{(f)\}}=\{(f)\}\cup\{(x-\alpha,y-\beta)\mid f(\alpha,\beta)=0\}$$というように"その曲線上にある"閉点らが余分に付け加わります。そのニュアンスを図に表しています。
- $(0)$には奇妙な図が描いてありますが、これは$\overline{\{(0)\}}=\Spec(A)$という事実に対応しています。つまり$(0)$は$\Spec(A)$のすべての点のいくらでも近くに存在している点であると考えなければならず、このように変な図になります。このような点は生成点(generic point)と呼ばれます。
以下のようにまとめておきましょう。
$\Spec(k[x,y])$は、$k^2$に適当な点を追加したものである。
また$k^2$は$\Spec(k[x,y])$の閉点、すなわち極大イデアル全体を取ることで復元される。
$\A_k^2\coloneqq\Spec(k[x,y])$とかき、これをアフィン平面と呼びます。
例2:$k[x,y]/\mfp$
$A=k[x,y]$は上の例と同じものを指すことにして、その素イデアル$\mfp=(f)$で割った環$A/\mfp$を考えてみましょう。
イデアルの対応定理などを踏まえると、$\Spec(A/\mfp)$は以下のように図示できるでしょう。
![!FORMULA[100][-1682661127][0]と!FORMULA[101][663157511][0]の関係の図示](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2FUjnoB9hSWNMtaWJXAQAc.jpg?alt=media) $\Spec(A/\mfp)$と$\Spec(A)$の関係の図示
$\Spec(A/\mfp)$と$\Spec(A)$の関係の図示
$\mfp$が新たな生成点となり、それ上の閉点のみがそっくりそのまま残っています。
自然な射影$$p:A\twoheadrightarrow A/\mfp$$はイデアルの対応定理による同相を通して自然な包含
$$p^*:V(\mfp)\cong \Spec(A/\mfp)\hookrightarrow\Spec(A)$$を誘導しています。
以下のようにまとめておきましょう。
素イデアルによる剰余環は、閉部分多様体に対応する。
自然な射影は、多様体間の包含写像に対応する。
「多様体」を定義していないので、あまり意味のない主張ではありますが...(次で定義します)
次はさらに具体的な例で計算してみましょう。
例3:2種類の$k[x]\to k[x,y]/(x^2-y)$
$A=k[x]\cong k[x,y]/(y),~B=k[x,y]/(x^2-y)$とおきます。ここでは$k$の標数は2ではないとしておきます。
一つ目
まず
$$\varphi:A\to B~;x\mapsto x$$
を自然な包含とします。
誘導される$\varphi^*:\Spec(B)\to\Spec(A)$は以下のように図示できます。
![!FORMULA[110][-1040528586][0]の図示](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2FdueAbMX2xL6cHBTOi1Tx.jpg?alt=media) $\varphi^*$の図示
$\varphi^*$の図示
ただし$A\cong k[x,y]/(y)$によって、$\Spec(A),\Spec(B)$をともに$\A_k^2$の閉部分多様体と見ています。
2つ目
次に、別の準同型として
$$\psi:A\to B~;x\mapsto y$$
を考えてみましょう。
誘導される$\psi^*:\Spec(B)\to\Spec(A)$は以下のように図示できます。
![!FORMULA[116][1678512202][0]の図示](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2FmjFLSmk0GssWDXhS80sU.jpg?alt=media) $\psi^*$の図示
$\psi^*$の図示
この図だけでは$\psi^*$が全射でないように見えますが、実際には$k$の代数閉性から全射になっています。$\R$のように実1次元で図示する限界が来ていますね...
![!FORMULA[120][1678512202][0]の図示’](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2F1bGrBsiN3O5YMSacVQmq.jpg?alt=media) $\psi^*$の図示’
$\psi^*$の図示’
下半分は、例えば$k=\C$なら虚部分からくるものです。
比較
$\varphi^*$と$\psi^*$を比べてみましょう。
$A$の素イデアル$\mfp=(x-\alpha)$に対し、$$\#\{\mfq\in\Spec(B)\mid\varphi^*(\mfq)=\mfp\}$$$$\#\{\mfq\in\Spec(B)\mid\psi^*(\mfq)=\mfp\}$$を調べます。
| $\varphi^*$ | $\psi^*$ | |
|---|---|---|
| $\alpha\neq0$ | 1 | 2 |
| $\alpha=0$ | 1 | 1 |
すなわち、$\varphi^*$は全単射ですが、$\psi^*$は0以外で2:1の写像であり、0でのみ1:1となっています。
上の図6を見てみると、青で描かれている$\Spec(B)$は赤で描かれている$\Spec(A)$をほとんどの場所で2重に被覆していますが、その被覆は原点で分岐つまり枝分かれしています。これについては整性・整閉性と幾何の章でも改めて少し触れます。
例4:$A=k[x_1,\cdots,x_n]$
一般の多変数多項式環について$\Spec$を考察するには、大きめの定理を使う必要があります。
多項式環$k[x_1,\cdots,x_n]$の極大イデアルは、$(\alpha_1,\cdots,\alpha_n)\in k^n$による
$$(x_1-\alpha_1,\cdots,x_n-\alpha_n)$$
のみである。
これによって、以下のようにまとめられます。
$\Spec(k[x_1,\cdots,x_n])$は、$k^n$に適当な点を追加したものである。
また$k^n$は$\Spec(k[x_1,\cdots,x_n])$の閉点、すなわち極大イデアル全体を取ることで復元される。
$\A_k^n\coloneqq\Spec(k[x_1,\cdots,x_n])$とかき、これをアフィン空間と呼びます。
根基と幾何(零点定理強形)
この章では$A=k[x_1,\cdots,x_n]$を$n$変数多項式環とします。
代数
環$A$のイデアル$\mfa$に対し、
$$\sqrt{\mfa}\coloneqq\{f\in A\mid\exists n,~f^n\in\mfa\}$$
とおくと、これは再び$A$のイデアルとなる。
これを$\mfa$の根基(radical)という。
$$\sqrt{\mfa}=\bigcap_{\mfa\subseteq\mfp}\mfp$$
である。
$\sqrt{\mfa}=\mfa$を満たすイデアルを、根基イデアルと呼ぶ。
幾何
任意の$T\subseteq A$に対し、$Z(T)\subseteq k^n$を
$$Z(T)\coloneqq\{(\alpha_1,\cdots,\alpha_n)\in k^n\mid \forall f\in T,~f(\alpha_1,\cdots,\alpha_n)=0\}$$
と定める(つまり$Z(T)=\{~T$に入っている多項式の共通零点$\}$である)。
$Z(T)$の形の部分集合(代数的集合と呼ぶ)全体を閉集合とすることで、$k^n$に位相が入る。この位相も Zariski 位相と呼ぶ。
代数的集合のうち、既約な(=真部分閉集合2つの合併で書けない)ものをアフィン代数多様体と呼ぶ。
$Z(-)$という、$A$の部分集合 に対して $k^n$の閉集合 を対応させる写像が定まりました。
これに対してある意味でほぼ逆になるべき写像を構成します。
任意の$Y\subseteq k^n$に対し、$I(Y)\subseteq A$を
$I(Y)\coloneqq\{f\in A\mid\forall (\alpha_1,\cdots,\alpha_n)\in Y,~f(\alpha_1,\cdots,\alpha_n)=0\}$
と定める(つまり$I(Y)=\{~Y$において零である多項式全体$\}$である)。
$I(Y)$は$A$のイデアルとなる。
$I(-)$は、$k^n$の部分集合 に対して $A$のイデアル を対応させる写像です。
この対応は、すぐ分かるところでは以下の全単射を与えます。
![!FORMULA[176][37422][0]と!FORMULA[177][36895][0]が定める全単射](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2Ftd7iU76HKtu2mM7owqsu.jpg?alt=media) $Z$と$I$が定める全単射
$Z$と$I$が定める全単射
さて、では
- 既約閉とは限らない$k^n$の部分集合は、$I$で送ってから$Z$で送るとどうなるだろうか?
- 素イデアルとは限らない$A$のイデアルは、$Z$で送ってから$I$で送るとどうなるだろうか?
解答は以下のようになります:
$Y$を$k^n$の任意の部分集合とするとき、
$Z(I(Y))=\overline{Y}$:$Y$の閉包
$\mfa$を$A$の任意のイデアルとするとき、
$I(Z(\mfa))=\sqrt{\mfa}$:$\mfa$の根基
特に、$A$の根基イデアルと$k^n$の閉集合には$Z$と$I$によって全単射が定まります。
![!FORMULA[196][37422][0]と!FORMULA[197][36895][0]が定める対応](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2FEYn0NElaap0TJafh0LXt.jpg?alt=media) $Z$と$I$が定める対応
$Z$と$I$が定める対応
$Z(\mfa)=Z(\sqrt{\mfa})$
図と例
$\mfa=(x^2,xy)$
$A=k[x,y]$とし、さらに$\mfa=(x^2,xy)$とおきます。
これの根基は$\sqrt{\mfa}=(x)$です。
これらが定める代数的集合は以下のものになります。
![!FORMULA[203][866067437][0]](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2FWVWrSFJ3PAKjw4YmuW7O.jpg?alt=media) $Z(\mfa)=Z(\sqrt{\mfa})$
$Z(\mfa)=Z(\sqrt{\mfa})$
同じ図形を定めています。
これは、"$Z(-)$を取ることによって情報が失われている"と解釈すべきです。
理想的には、空間と環の等価性のような結果を得られたら嬉しい気がします。
その点において、$Z(-)$が単射でないという事実は、「空間から環を復元できない」ということを意味しており、まずいです。
空間だけでは環を復元できません。
ここで、空間に付加的な情報を添加することで、「空間$\!\!{}+\alpha$」から環を復元できるようにしたい気持ちがあります。スキーム論においては、構造層と呼ばれる対象がこの「$\!\!{}+\alpha$」を担いますが、これはまた別の機会に...。
ですがひとまずは、根基を取ることでどの程度の情報が失われるのかをもう少し精密に、代数的に考察してみましょう。
イデアルの分解と幾何(Lasker-Noether の定理)
整数の素因数分解の類似である、イデアルの準素分解について幾何的な解釈を考えます。
代数
環$A$の任意のイデアルが有限生成であるとき、$A$は Noether 環であるという。
これを定義として採用するのは気持ち悪いですが、一番簡単に書けるのがこれなので...
環$A$のイデアル$\mfq\neq A$が
$$xy\in\mfq\Rightarrow x\in\mfq~~\mathrm{or}~~y\in\sqrt{\mfq}$$
を満たすとき、$\mfq$は準素イデアル(primary ideal)であるという。
準素イデアルの根基は素イデアルとなる。
素イデアルの定義が
$$xy\in\mfp\Rightarrow x\in\mfp~~\mathrm{or}~~y\in\mfp$$
だったことを考えると、準素イデアルは素イデアルの一般化になっています。
Noether 環$A$の任意の真のイデアル$\mfa$に対して、ある準素イデアル$\mfq_1,\cdots,\mfq_n$が存在し、
$$\mfa=\mfq_1\cap\cdots\cap\mfq_n$$
と表示できる。このような表示を準素分解(primary decomposition)と呼ぶ。
$k[x_1,\cdots,x_n]$は Noether 環である。
$k[x_1,\cdots,x_n]$の任意の真のイデアルは準素分解可能である。
幾何
- $A$の準素イデアル$\mfq$に対し、$Z(\mfq)$は既約閉集合、すなわちアフィン代数多様体である。
- $f,g\in A$が互いに素なら$Z((f)\cap(g))=Z((f))\cup Z((g))$
これらを合わせると、例えば$\mfa$の準素分解が
$\mfa=(f_1)\cap\cdots\cap(f_n)$
と互いに素な$f_1,\cdots,f_n\in A$によって書けるとき、
$Z(\mfa)=Z((f_1))\cup\cdots\cup Z((f_n))$
は$Z(\mfa)$の既約分解のように見えてきます。
図と例
この図と例では$A=k[x,y]$とします。
$\mfa=\left(x(x-y+1)\right)$
$\mfa$の準素分解は、
$\mfa=(x)\cap(x-y+1)$
により与えられます。
これに対応して、それぞれが定める図形は以下のようになります。
![!FORMULA[235][-1646108507][0]](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2FmLzcHIdJMdMJia6sYcDI.jpg?alt=media) $\mfa=(x(x-y+1))$
$\mfa=(x(x-y+1))$
自明な例でしたね...
$\mfa=(x^2,xy)$
前の章で出した例ですね。準素分解は
$\mfa=(x)\cap(x,y)^2$
となります。
![!FORMULA[238][-1375235529][0]](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2FAnvfLE1m0IyaXU1ENXZ8.jpg?alt=media) $\mfa=(x^2,xy)$
$\mfa=(x^2,xy)$
前の状況とずいぶん変わってしまいました。$(x)$の方だけで十分に思えますが、実際には原点で2重に重なっている点とでもいうべき$(x,y)^2$が現れてしまいます。
これは、代数的には$(x)=\sqrt{(x)}$と$(x,y)=\sqrt{(x,y)^2}$の間に包含関係があることに起因しています。この例での$(x,y)^2$のように、準素分解において根基が極小でないような成分は埋入(embedded)であるといいます。$k^n$においてまさに「埋まっている」図形を定めることが由来の名前です。
さて、このような「埋まっている」図形、あるいは「重なっている」図形は、$k^n$に移った時点で失われてしまう情報ということになります。以下のようにまとめておきましょう。
$\mfa=\mfq_1\cap\cdots\cap\mfq_n$を準素分解とするとき、$Z(\mfa)$から復元できるのは$\mfp_i=\sqrt{\mfq_i}$らの中で極小な素イデアル(孤立素因子)の情報までである。
整性・整閉性と幾何(Cohen-Seidenberg の定理)
代数
$\varphi:A\to B$を環準同型とする。
$b\in B$が$A$上整であるとは、$a_1,\cdots,a_n\in A$が存在し、
$$b^n+\varphi(a_1)b^{n-1}+\cdots+\varphi(a_n)=0$$
となることをいう。全ての$B$の元が$A$上整であれば、$B$は$A$上整である、または$\varphi:A\to B$は整であるという。
整域$A$が整閉であるとは、$A$の商体を$K$とするとき
$\{x\in K\mid x$は$A$上整$\!\}=A$であることをいう。
幾何
$\varphi:A\to B$が整であれば、誘導される
$\varphi:\Spec(B)\to\Spec(A)$は全射かつ閉写像である。
整であるという条件が$\Spec$の間の連続写像として非常にわかりやすく良い性質をもっているというのは、あまり直感的に分かることではないと思います。
"整"の幾何的な良さをさらに精密に調べるには、少し複雑な可換環論の定理が必要になります。
代数
以下に述べる上昇定理と下降定理をあわせて Cohen-Seidenberg の定理と言います。
$A\subseteq B$を環の整拡大とする、すなわち包含写像$i:A\hookrightarrow B$が整であるとする。
$A$の素イデアル$\mfp_1,\mfp_2$と、$B$の素イデアル$\mfq_1$が以下を満たすとする。
- $\mfp_1\subseteq\mfp_2$
- $\mfq_1\cap A=\mfp_1$
このとき$B$のある素イデアル$\mfq_2$が存在し、以下を満たす。
- $\mfq_1\subseteq \mfq_2$
- $\mfq_2\cap A=\mfp_2$
$\mfq\mapsto\mfq\cap A$は、包含写像$i:A\hookrightarrow B$から誘導される
$i^*:\Spec(B)\to\Spec(A)$といっても同じことです。
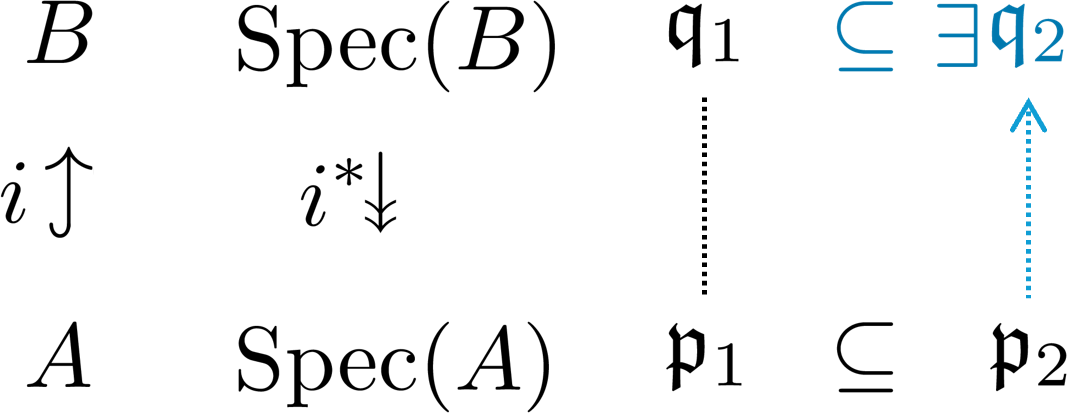 上昇定理
上昇定理
↑ 見る人が見たら卒倒する図だと思いますが、$\LaTeX$力がないので他ツールで無理やり図式を作っています。ごめんなさい...
$A\subseteq B$を環の整拡大とし、さらに$A,B$は整域で$A$は整閉だとする。
$A$の素イデアル$\mfp_1,\mfp_2$と、$B$の素イデアル$\mfq_2$が以下を満たすとする。
- $\mfp_1\subseteq\mfp_2$
- $\mfq_2\cap A=\mfp_2$
このとき$B$のある素イデアル$\mfq_1$が存在し、以下を満たす。
- $\mfq_1\subseteq \mfq_2$
- $\mfq_1\cap A=\mfp_1$
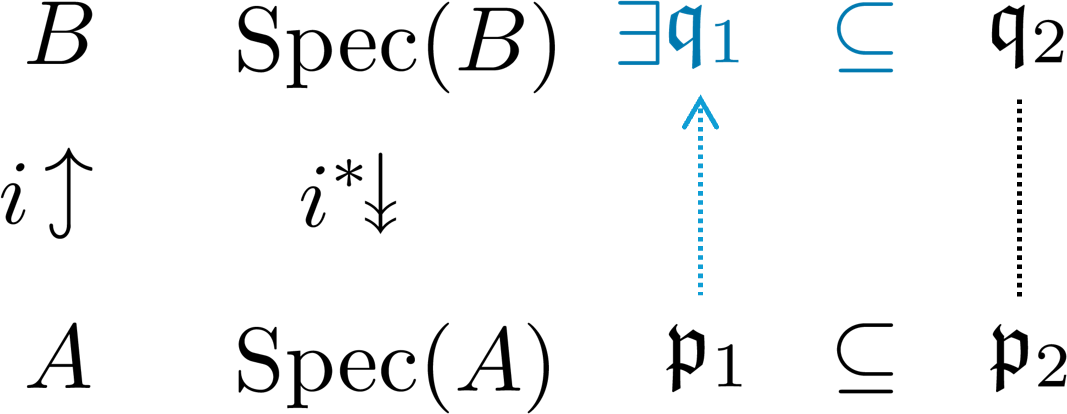 下降定理
下降定理
代数的にも十分面白いことを言っている定理ですが、$\Spec$の間の連続写像として観察すると、特に下降定理において面白い手触りがあります。
幾何
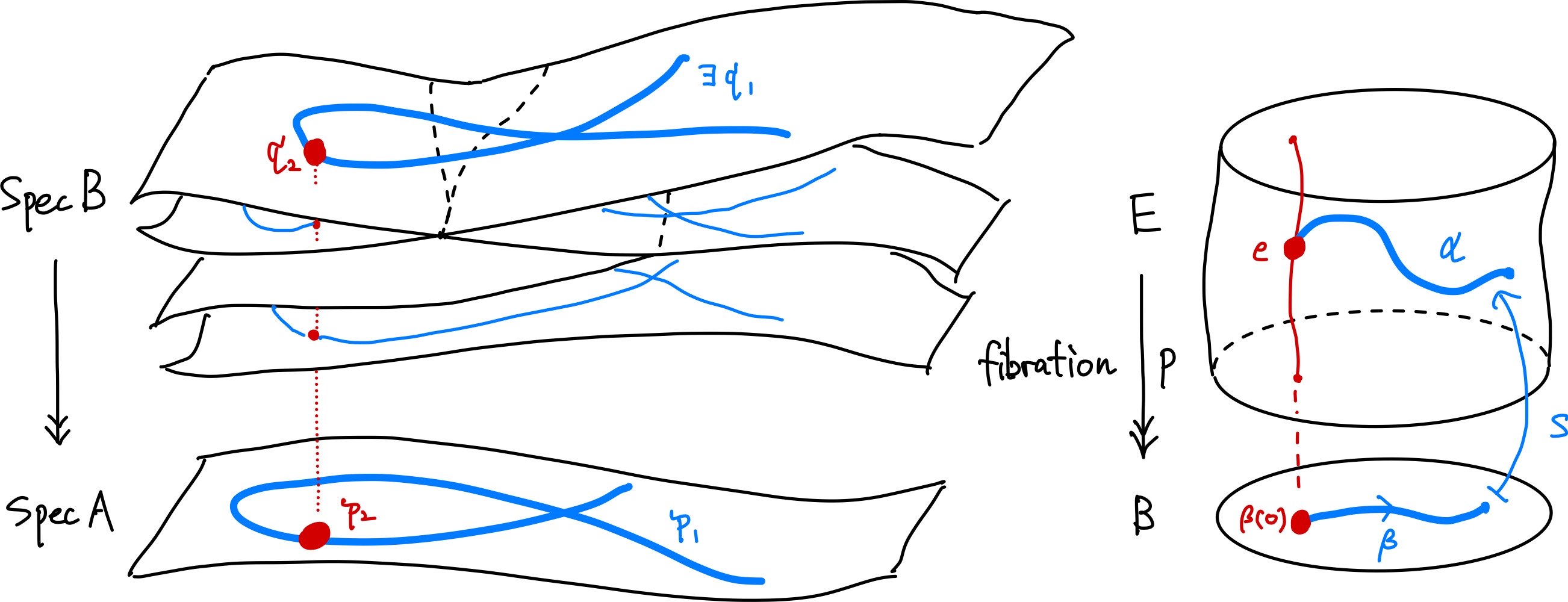
下降定理の状況を模式図に表してみます。実際の状況とは程遠いあまりにも無茶苦茶な図ですが、下降定理の主張を把握するのには役立つと思います。
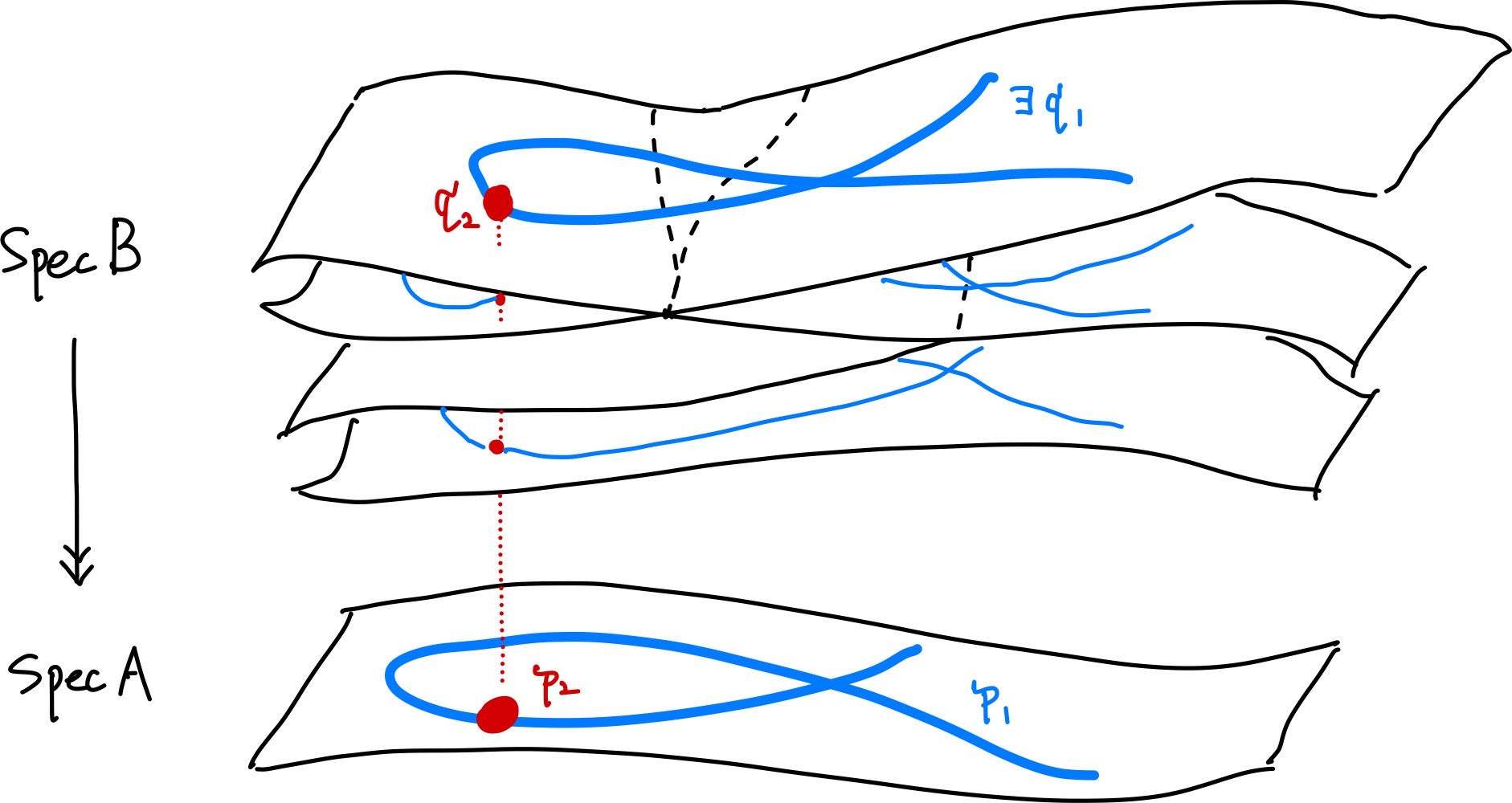 下降定理
下降定理
$\mfp_1\subseteq\mfp_2\in\Spec(A)$と$\mfq_2\in\Spec(B)$を指定したときに、
- $\mfq_2$を通るように$\mfp_1$をリフトした$\mfq_1\in\Spec(B)$を取ってくることができる
というのが下降定理の主張でした。
"素イデアルが縮小する"ことは"図形が拡大する"ことに対応するので、下降定理は
"$\Spec(A)$における図形の拡大を、$\Spec(B)$において指定した図形の拡大に持ち上げることができる"というような性質になっています。
かなり無理やりですが、この性質は被覆空間、あるいはより一般に空間の fibration が持つ path lifting と呼ばれる性質に類似しています。
急ですが、ここでは位相空間と言ったら compactly generated weak Hausdorff 空間を意味するものとします(当然$\Spec$はそのような良い性質は満たしませんが...)。
fibration とは、ファイバー束のある意味での一般化であり、位相空間においていい感じに振る舞ってくれる全射のクラスです。
位相空間の全射連続写像$p:E\to B$が (Hurewicz)fibration であるとは、$p$を含む任意の可換図式
![!FORMULA[308][36467630][0]は!FORMULA[309][-1798584343][0]](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2FspsY7IMeoPa7M0ENGO7Y.png?alt=media) $i_0$は$y\mapsto(y,0)$
$i_0$は$y\mapsto(y,0)$
に対し、図式を可換にする$h$のリフト$\tilde{h}$が存在することをいう。
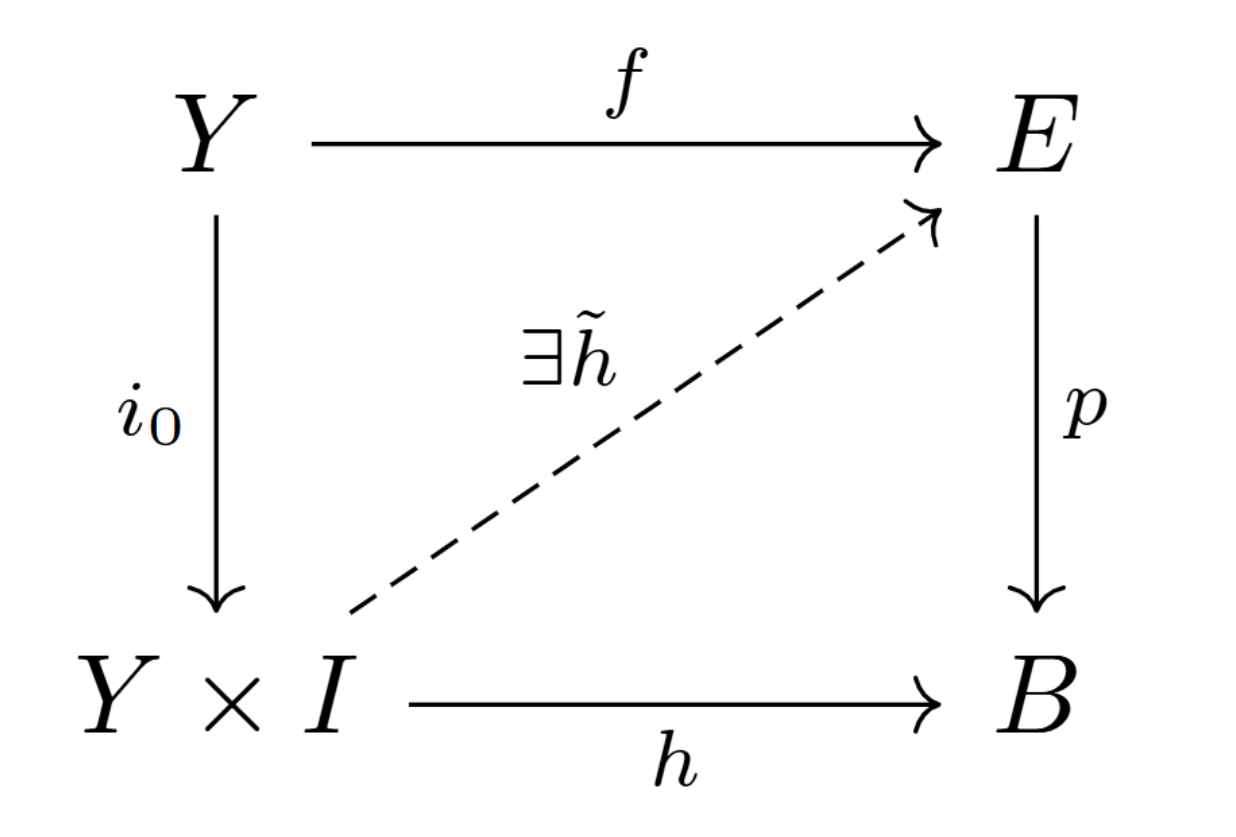 リフトの存在
リフトの存在
この性質を CHP(Covering Homotopy Property) と呼ぶ。
$Np=E\times_p B^I$を$p$の mapping path space とするとき、$p$が fibration であることは以下の図式を可換にする$s:Np\to E^I$が存在することと同値である。
![!FORMULA[316][36676167][0]は!FORMULA[317][-1260280279][0]](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2FJppcrbFkjPsb2mUGOTUV.png?alt=media) $p_0$は$\beta\mapsto\beta(0)$
$p_0$は$\beta\mapsto\beta(0)$
$s:Np=E\times_p B^I\to E^I$は、
- $e\in E$と$\beta\in B^I$の組であって$\beta(0)=p(e)$なるもの
を
- $\alpha\in E^I$であって$\alpha(0)=e$かつ$p\circ\alpha=\beta$なるもの
にうつします。
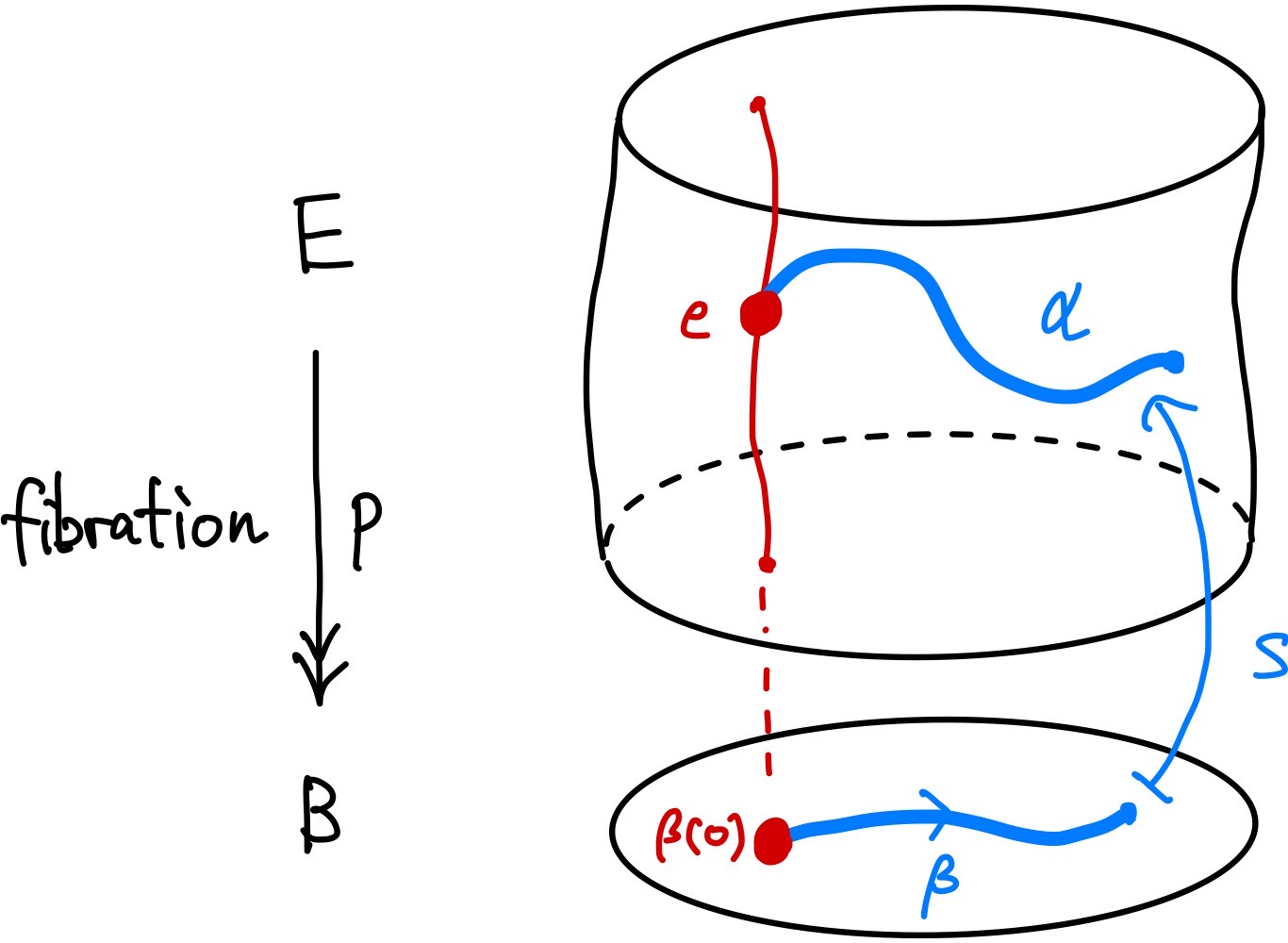 道を"持ち上げる"
道を"持ち上げる"
$s$は path lifting fuction といいます。
並べてみましょう。
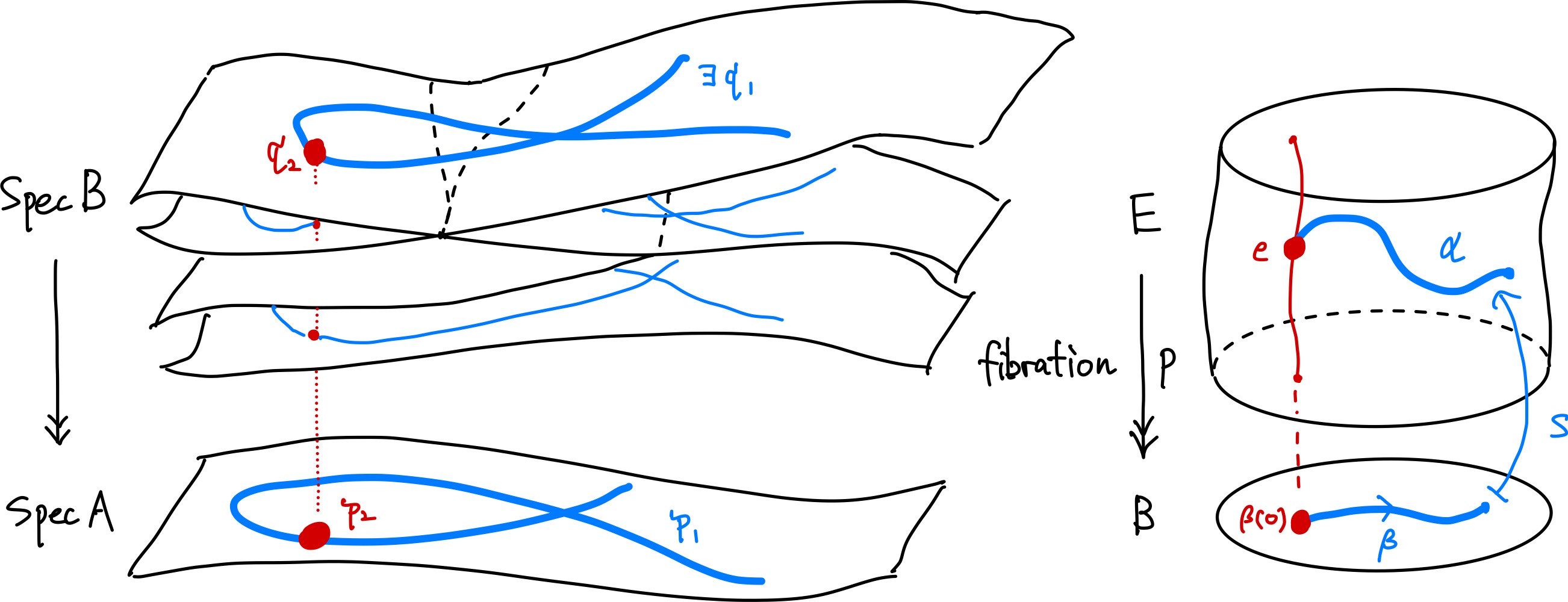 下降定理と fibration の比較
下降定理と fibration の比較
似ていますね(?)
fibration における幾何的直観を下降定理に持ち込み、以下のようにまとめておきましょう。
環準同型の整性や環の整閉性は、$\Spec$の間の射が"いい感じの""被覆っぽく"なっていることを担う。
被覆空間との正確な対応物は、考える場所をスキームに移したうえで、その間の étale 射を考えることで与えられるはずです。勉強したらまた書くかもしれません。
Conclusion
代数として学んだ内容が$\Spec$を通して幾何的なイメージとして立ち上がってくるのは、個人的にはどうしようもなく面白いのですが、いかがだったでしょうか。特に整性なんて代数的整数論のおおもとではありますが、それが被覆っぽさを持っているなんて、まったくもって非自明で興味深いことです。
本当は、この記事で構造層まで定義したうえで
- 特異点の様子を各点での局所環に対する純環論的な操作によって調べる
という超絶面白い議論まで含みたかったのですが、間に合いませんでした...
後編もいつか書くので読んでいただけたらうれしいです!
