コリオリ力と遠心力を複素平面上で求める。
複素平面上でコリオリ力と遠心力を求める。
座標系として慣性系と回転系の二つの座標を考える。
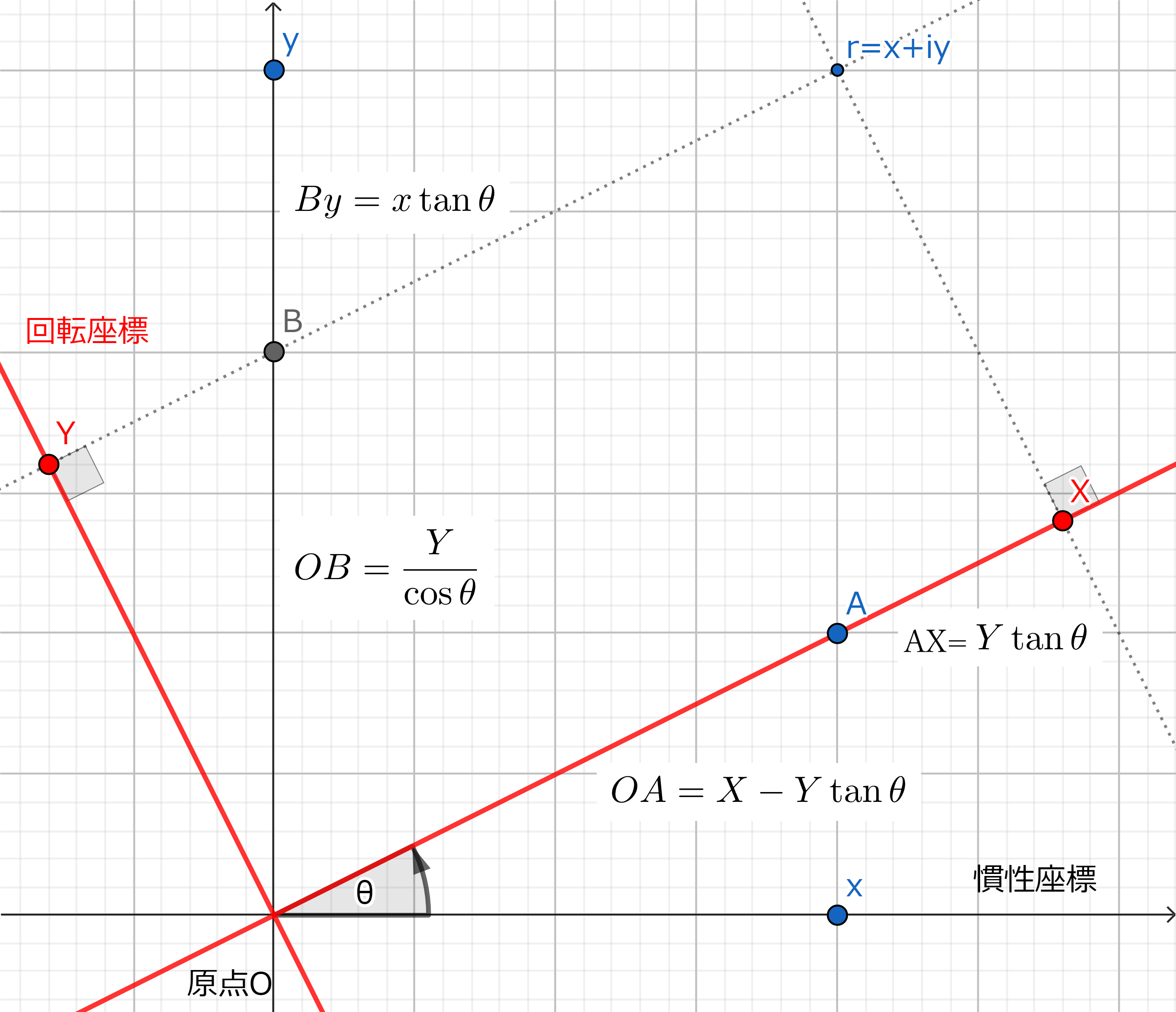回転座標と慣性座標
慣性系上の質点の座標を$r=x+iy$、一定の角速度$ω$で回転し、時刻$t$における角度が$θ(t)=ωt$になる回転系上の座標$R=X+iY$であらわすと
$$
\BEQ
x
&=&(X-Y\tan\theta) \cos\theta\\
&=&X\cos\theta-Y\sin\theta\\
y
&=&\frac{Y}{\cos\theta}+x\tan\theta\\
&=&\frac{Y}{\cos\theta}+X\sin\theta-Y\frac{\sin^2\theta}{\cos\theta}\\
&=&X\sin\theta+\frac{Y-Y\sin^2\theta}{\cos\theta}\\
&=&X\sin\theta+Y\cos\theta\\
\EEQ
$$
よって慣性系座標$r$は回転系座標$R$を使って
$$
\BEQ
r
&=&x+iy\\
&=&X\cos\theta-Y\sin\theta+i(X\sin\theta+Y\cos\theta)\\
&=&X(\cosθ+i\sinθ)+Y(-\sinθ+i\cosθ)\\
&=&X(\cosθ+i\sinθ)+iY(-\frac1i \sinθ+\cosθ)\\
&=&X(\cosθ+i\sinθ)+iY(i\sinθ+\cosθ)\\
&=&(X+iY)(\cosθ+i\sinθ)\\
&=&Re^{iθ}\\
\EEQ
$$と簡潔に表せる。次に$r$を$t$で２階微分して
$$
\BEQ
\dot{r}&=&\dot{R}e^{iθ}+Riωe^{iθ}=(\dot{R}+iωR)e^{iθ}\\
\ddot{r}
&=&(\ddot{R}+iω\dot{R})e^{iθ}+(\dot{R}+iωR)iωe^{iθ}\\
&=&(\ddot{R}+iω\dot{R}+iω\dot{R}-ω^2R)e^{iθ}\\
&=&(\ddot{R}+2iω\dot{R}-ω^2R)e^{iθ}\\
\EEQ
$$
よって、質点の質量を$m$としたときの運動方程式は
$$
\BEQ
m\ddot{r}&=&(\ddot{R}+2iω\dot{R}-ω^2R)me^{iθ}\\
\EEQ
$$となる。ここで質点$m$に力が加わっていない状態を考える。
つまり$\ddot{r}=0$のとき、上式は
$$
\BEQ
0&=&(\ddot{R}+2iω\dot{R}-ω^2R)me^{iθ}\\
\EEQ
$$となり式を整理して
$$\BEQ
m\ddot{R}
&=&-2imω\dot{R}+mω^2R\\
&=&2mω(-i\dot{R})+mω^2R
\EEQ$$を得る。
左辺の次元は力の次元。よって右辺の各項も力の次元である。
右辺第一項がいわゆるコリオリ力、第二項が遠心力である。
また第一項には$-i$が掛けられていることから、コリオリ力の方向は速度ベクトル$\dot{R}$の方向から時計回りに９０度回転した方向に一致することもわかる。また遠心力の方向は$R$の増加方向と一致することもわかる。
