微分方程式の数値解法とその実装
初投稿です.
東京大学理科Ｉ類B2,理学部物理学科内定のLucreziaです.
本記事はPhysics Lab. Advent Calender2026への寄稿です.
今回は私が興味を持っている数値シミュレーションで用いられる,微分方程式の初期値問題の数値解法に関して説明していきます.
初歩的な内容に留まり,不正確な記述もあるかと思いますので,研究されている方や詳しい方も温かい目で御覧ください.
動機
微分方程式は物理学に於いて現象の記述によく用いられる.
例えば,運動方程式
$$\dot{\boldsymbol p}(t)=\boldsymbol F$$
とは,右辺の外力の項の作用によって運動量が変化すると言う状況を記述している.
しかし,一般的な微分方程式は初等関数で書き表されるような解を持っているとは限らない.
また,得られた解が扱いやすいものとも限らない.
特に,シミュレーションなど実践的な場面においては,解の関数としての形よりも,微分方程式を満たす関数が存在するとき引数を変化させると関数の振る舞いがどう変わるかのほうが重要になることがある.
そこで活躍するのが数値解法と呼ばれる解析手段である.
この手段を取ることによって,実際に解の関数を求めることなく,関数の振る舞いを確認できる.
(注釈)：微分方程式は任意の未定定数を含んだ関数を解に持つ.そのため解を一意に定めるには付加的条件が必要になる.これによる分類が初期値問題と境界値問題である.初期値問題は解の特定の一点の情報を指定することで,境界値問題は変数の端点における情報を指定することで,それぞれ一意性をもたせる.例えば運動方程式を与えて,時刻0での位置と速度から時間発展を考察する場合は初期値問題,解析力学の最小作用を考える際に微小変分を初期時刻と終了時刻で0とするという条件を与えているのは境界値問題といえる.この記事では初期値問題の考察を行うこととする.
Euler 法
陽的Euler法
最も単純な数値解法が陽的Euler法である.
陽的という言葉の意味は後で紹介する.
次の一変数の微分方程式の初期値問題を考える.
\begin{align} \frac{d}{dt}x(t)=f(t,x(t)) \end{align}
このとき,$f$は必ずしも$t$で積分できなくても良い.
微分の定義
$$ \frac{d}{dt}x(t)=\lim_{\Delta t\to0}\frac{x(t+\Delta t)-x(t)}{\Delta t}$$
より,十分に小さい$\Delta t$に対して
$$\frac{x(t+\Delta t)-x(t)}{\Delta t}\simeq f(t,x(t))$$
となることが分かる.(誤差は後ほど評価する)
ここで,この方程式を漸化式に書き換えることを考える.
引数$t$の範囲を閉区間$[t_{i},t_f]$として区間を$N$等分する.
すなわち,
$h:=\dfrac{t_f-t_i}{N}$
とする.
$t_n:=t_i+nh$と定め,次の漸化式を作る
\begin{align}
\begin{cases}
x_0=x(t_i)\\
x_{n}=x_{n-1}+hf(t_{n-1},x_{n-1})\qquad (n=1,2,...N)
\end{cases}
\end{align}
この漸化式は,上で示した微分方程式の近似で
$t\to t_{n-1}$,$\Delta t\to h$,$x(t)\to x_{n-1}$としたものである.
漸化式を帰納的に解いていくことで,$(t_n,x_n)$の組が得られる.
この解法を陽的Euler法と呼ぶ.
陽的Euler法はどの程度誤差が生じるのだろうか.
かなり大胆な近似をしているため,余り精度は良くないと見込まれる.
評価に当たっては,真の値$x(t_n)$との誤差$e_n:=x(t_n)-x_n$と定め,これの収束性を考えれば良い.
以下では,$t$による微分はLagrangeの記法を用いて$\dfrac{d}{dt}x=x'$と書くことにする.
また,問題の条件を厳しくして,得られる関数$x(t)$が$C^2$級であり,右辺の関数$f(t,x)$が$x$に対してLipschitz連続であるとする.
ただし,Lipschitz連続とは次を満たすことで,通常の連続性よりも厳しい条件である.
この条件をなくすと,以下の議論で扱う誤差の収束が成り立たなくなる.
実関数$g(x)$に対して$\exists\,L>0,\forall x,y\in\mathbb{R}$
$$|g(x)-g(y)|< L|x-y|$$
このLをLipschitz定数と呼ぶ.
例えば,連続関数$g(x)=x^{\frac{1}{3}}$は原点付近で傾きが発散するためLipshitz連続でない.
問題1の微分方程式に関して,次の定理が成り立つ.
$f(t,x)$が$x$に関してLipschitz連続かつ$x$が$C^2$級のとき
$$|e_n|< Ch$$
ただし,$C$は$h,t$に依存しない定数.
この定理が主張することは,陽的Euler法は引数の刻み幅$h$の1乗の精度であるということである.
これを示したい.
証明に当たって,いくつか補題を示す.
まず,$x$が$C^2$級であることから次の補題2が従う.
$ \exists M>0,$
$$\frac{1}{2}\max_{t\in[t_i,t_f]}|x''(t)|< M$$
次に,補題3を考える
$L$:$f$のLipschitz定数, $n=0,1,2,....N-1$
$$|e_{n+1}|<(1+hL)|e_n|+h^2M$$
$x(t_{n+1}) $を$t_n$の周りでTaylor展開すると,Taylorの定理からある実数$0<\theta<1$を用いて
$$x(t_{n+1})=x(t_n)+hx'(t_n)+\frac{h^2}{2}x''(t_n+h\theta)$$
と書くことができる.これは$x$が$C^2$級であることから保証される.
\begin{align}
\frac{e_{n+1}-e_n}{h}=&\frac{x(t_{n+1})-x(t_n)}{h}-\frac{x_{n+1}-x_n}{h}\\
=&x'(t_n)+\frac{h}{2}x''(t_n+h\theta)-f(t_n,x_n)\\
=&f(t_n,x(t_n))-f(t_n,x_n)+\frac{h}{2}x''(t_n+h\theta)
\end{align}
分母を払って絶対値を取り,Lipschitz連続性と補題2を用いて,
\begin{align}
|e_{n+1}|&\le|e_n|+h|f(t_n,x(t_n))-f(t_n,x_n)|+\frac{h^2}{2}|x''(t_n+h\theta)|\\
&\le(1+hL)|e_n|+h^2M
\end{align}
これは補題3である.$\Box$
$\forall n\in\{1,2,3....N\}$
$$|e_n|\le (1+hL)^n|e_0|+\sum_{j=0}^{n-1}h^2M(1+hL)^j$$
$n=1$のときは補題3そのものである.
$n=k$のとき,補題4が成り立つとする.このとき,$n=k+1$では補題3より
\begin{align}
|e_{k+1}|&\le(1+hL)|e_k|+h^2M\\
&\le(1+hL)\left((1+hL)^k|e_0|+\sum_{j=0}^{k-1}h^2M(1+hL)^j\right) +h^2M\\
&=(1+hL)^{k+1}|e_0|+\sum_{j=0}^{k-1}h^2M(1+hL)^{j+1}+h^2M\\
&\le(1+hL)^{k+1}|e_0|+\sum_{j=0}^{k}h^2M(1+hL)^j
\end{align}
従って,$n=k+1$でも成立するから,帰納的に補題4が示された.$\Box $
これを用いて定理1を示す.
陽的Euler法では,$e_0=0$だから補題4は次の形になる:
$$|e_n|\le\sum_{j=0}^{n-1}h^2M(1+hL)^j=h^2M\times\frac{(1+hL)^n-1}{hL}=\frac{M\{(1+hL)^n-1\}}{L}h$$
ここで、$e^x\ge1+x$を用いて,$1+hL>1$と合わせて
$$|e_n|<\frac{M}{L}(\exp(hLN)-1)h$$
従って,$C:=\dfrac{M}{L}(\exp(hLN)-1)$とすれば,定理1が得られる.$\Box$
このことから,$f$がLipschitz連続かつ$x(t)$が$C^2$級であるという条件のもとでは,陽的Euler法は刻み幅の1次の精度である.
余談であるが,Feynmanの力学の教科書に惑星の運動を数値計算で導く方法が紹介されているが,採用されているのはこの陽的Euler法である.
陰的Euler法
陽的Euler法では漸化式の右辺は添字が$n$の量のみに依存していた.
陽的とはこのことを指す.
陰的Euler法では右辺に$n+1$の添字を持つ量を用いる.
具体的には同じ微分方程式に対して次のように漸化式を定める.
$$ \frac{x_{n+1}-x_n}{h}=f(t_{n+1},x(t_{n+1}))$$
この漸化式は陽的法のように右辺に$x_n$を代入して計算するだけでは解くことができず,一般に個別に$x_{n+1}$について解く必要がある.
$x_{n+1}$の表式に$_{n+1}$が現れるため,この名称がついている.
その代わりとして,陽的法と比較して安定性が高いという利点がある.(安定性の定義はのちに示す)
具体例を見ることにする.
次の微分方程式を考える.
$$\frac{d}{dt}x(t)=\lambda x(t) $$
これは容易に解くことができ,解は$x(t)=1$のもとで
$$x(t)=\exp(\lambda t)$$
となる.
Lipschitz定数は$\lambda$になっている.
この方程式を陽的Euler法で計算するとき,漸化式は
\begin{align}
\begin{cases}
x_0&=1\\
x_{n+1}&=(1+h\lambda)x_n
\end{cases}
\end{align}
である.
これは単純な等比数列より,一般項は
$$x_n=(1+h\lambda)^n$$
一方で陰的Euler法の場合,
\begin{align}
\begin{cases}
x_0&=1\\
x_{n+1}&=x_n+h\lambda x_{n+1}\,\iff x_{n+1}=\dfrac{1}{1-h\lambda}x_n
\end{cases}
\end{align}
である.こちらも単純な等比数列より,一般項は
$$x_n=\left(\dfrac{1}{1-h\lambda}\right)^n$$
$t\to\infty$とした時,解が収束するか考える.
陽的Euler法では$|1+h\lambda|<1$で収束する.
複素平面上では,$|1+z|<1$は$z=-1$を中心とする半径$1$の円内が収束条件となる.
実数の範囲で収束性を得るには,刻み幅を$\dfrac{2}{|\lambda|} $より小さく取る必要がある.
対して陰的Euler法では$\left|\dfrac{1}{1-h\lambda}\right|<1$が収束条件であり,これは$\lambda<0$では常に満たされる.
このことを$A-$安定と呼ぶ.
$\lambda$が非常に大きい方程式を硬い方程式と呼ぶが,こういった場合,陽的法を適用するのは不適切なため,陰的法を用いるのが良い.
次の図が,陽的Euler法と陰的Euler法で硬い方程式
$$\dfrac{d}{dt}x=-10x$$
のシミュレーションを行なったものである.
陽的法では解が発散している様子が見てとれる.
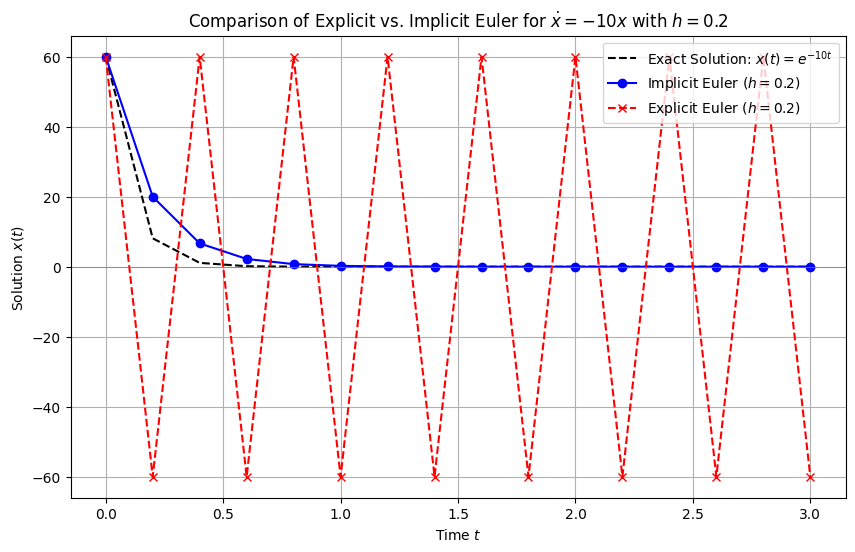硬い方程式のシミュレーション
Runge-Kutta法
Euler法は漸化式が単純であるというメリットこそあるが,精度が刻み幅の1乗のオーダーであるため,実用性に欠く.
数値シュミレーションは計算機で行うことを考えると,演算の回数は可能な限り減らしたい.
また,Taylor展開をして高次の微分を入れ込むことで精度を高める事も考えられるが,右辺の関数が微分できなかったり微分した関数の扱いが悪かったりした場合,解析に利用することが難しい.
その結果,実用的に要求される性質は次の二点となる:
- 高階微分を行わなくて良い
- 刻み幅$h$に対して$h^2$以上の精度を持つ
そこで,刻み幅の$t_n$と$t_{n+1}$の間に参照点を取って近似に導入することを考える.
問題1の微分方程式に対して,$s$段Runge-Kutta法を次で定める.ただし$s\in\mathbb{N}$
\begin{align}
\begin{cases}
x_0&=x(t_i)\\
x_{n+1}&=x_n+h\displaystyle{\sum_{l=1}^sb_lk_l}
\end{cases}
\end{align}
ただし,$k_l$は次で定める.
$$k_l=f\left(t_n+c_lh,x_n+\sum_{j=1}^sa_{lj}b_j\right) $$
$$\sum_{j=1}^sa_{lj}=c_j$$
係数は次のButcher配列で表記し,目標の精度が得られるように設定する.
\begin{align}
\begin{array}{c|cccc}
c_1&a_{11}&a_{12}&\cdots&a_{1s}\\
c_2&a_{21}&a_{22}&\cdots&a_{2s}\\
\vdots&\vdots&\vdots&\ddots&\vdots\\
c_s&a_{s1}&a_{s2}&\cdots&a_{ss}\\\hline
&b_{1}&b_{2}&\cdots&b_s
\end{array}=
\begin{array}{c|c}
\boldsymbol c&A\\\hline
&{}^t\boldsymbol b
\end{array}
\end{align}
$A$を下三角行列に設定すれば,$k_l$を定めるときに添字が$l$未満の情報のみを用いることになる.
これを陽的Runge-Kutta法と呼ぶ.
$A$が下三角行列ではない陰的法を考えれば,Euler法同様に高い安定性を得ることができる.
RK4
よく用いられるRunge-Kutta法に分類される手法に古典的Runge-Kutta法(RK4)と呼ばれるものが存在する.
これは以下のButcher配列で表現される.
$$\begin{array}{c|cccc}
0&\\
\dfrac{1}{2}&\dfrac{1}{2}\\
\dfrac{1}{2}&0&\dfrac{1}{2}\\
1&0&0&1&\\\hline
&\dfrac{1}{6}&\dfrac{1}{3}&\dfrac{1}{3}&\dfrac{1}{6}
\end{array}$$
この手法は刻み幅の4乗の精度である.
証明は省くが,$x(t_{n+1})=x(t_n+h)$の$t_n$周りのTaylor展開とRK4の漸化式で与えられた差分を比較して評価すれば良い.
RK4はプログラムが簡単な割に高い精度を得られるため,シミュレーションを行う際に便利な手法と言える.
埋め込み型Runge-Kutta法
通常のRunge-Kutta法では誤差評価を行わない.
誤差評価を行うためには$f(t,x)$の高階微分が必要になるが,数値計算においては微分を行うことは計算コストが高い.
そこで誤差評価を行うためのRunge-Kutta法の計算を同時に行い,刻み幅制御にフィードバックすることを考える.
誤差が大きければ刻み幅を細かくし,誤差が小さければ刻み幅を粗めに取るというようにすれば,効率よく演算できる.
一般のButcher配列は次
$$\begin{array}{c|c}
\boldsymbol c&A\\\hline
&{}^t\boldsymbol b\\\hline
&{}^t\tilde{\boldsymbol b}
\end{array} $$
$\tilde{\boldsymbol b}$が刻み幅制御用のものである.
この例として,Gauss-Legendre配列をあげる.
これは,陰的Runge-Kutta法の一種である.
Butcher配列は以下の通り.
$$
\begin{array}{c|c}
\boldsymbol c&A\\\hline
&{}^t\boldsymbol b\\\hline
&{}^t\tilde{\boldsymbol b}
\end{array}
\qquad
=
\qquad
\begin{array}{c|cc}
\dfrac{1}{2}-\dfrac{\sqrt{6}}{3}&\dfrac{1}{4}&\dfrac{1}{4}-\dfrac{\sqrt{6}}{3}\\
\dfrac{1}{2}+\dfrac{\sqrt{6}}{3}&\dfrac{1}{4}+\dfrac{\sqrt 6}{3}&\dfrac{1}{4}\\\hline
&\dfrac{1}{2}&\dfrac{1}{2}\\\hline
&\dfrac{1+\sqrt 3}{2}&\dfrac{1-\sqrt 3}{2}
\end{array}$$
多変数での扱い
ここまでは問題1で扱ったような1変数の場合を考察した.
しかし,実際の問題では常微分方程式であっても独立変数$t$に対する従属変数が複数存在したり,偏微分方程式を扱ったりと,多変数量を扱うことが多い.
ここでは,のちに触れる実装を考えて(厳密性は置いて)その取り扱いを考える.
まず,次の連立一階常微分方程式を考える.
\begin{align} \begin{cases} \dfrac{d}{dt}x=f_x(t,x,y,z,...)\\ \dfrac{d}{dt}y=f_y(t,x,y,z,....)\\ \dfrac{d}{dt}z=f_z(t,x,y,z,....)\\ \quad\vdots \end{cases} \end{align}
これに関しては,変数をベクトルとして扱えば一変数の場合に帰着できる.
つまり
$$\boldsymbol x:={}^t(x,y,z,....)$$
$$\boldsymbol F(t,\boldsymbol x):={}^t(f_x(t,\boldsymbol x),f_y(t,\boldsymbol x),f_z(t,\boldsymbol x),....) $$
と定めて,方程式を
$$\dfrac{d}{dt}\boldsymbol x=\boldsymbol F(t,\boldsymbol x)$$
と書き直せば,漸化式で定めた数列をベクトル列に置き換えることで同様に数値解法を構成できる.
次に,高階微分を含む場合を考える.
$$\dfrac{d^n}{dx^n}x=f\left(t,x,\dfrac{d}{dt}x,\dfrac{d^2}{dt^2}x,...,\dfrac{d^n}{dt^n}x \right)$$
この問題に関しては次のように考える.
次のように書き換える.
$$x_{(0)}=x,x_{(i)}=\dfrac{d^i}{dt^i}x\quad (i=1,2,3...n-1)$$
この時,
\begin{align}
\begin{cases}
\dfrac{d}{dt}x_{(0)}&=x_{(1)}\\
\dfrac{d}{dt}x_{(1)}&=x_{(2)}\\
\quad \vdots&\\
\dfrac{d}{dt}x_{(n-2)}&=x_{(n-1)}\\
\dfrac{d}{dt}x_{(n-1)}&=f(t,x_{(0)},x_{(1)},...,x_{(n-1)})
\end{cases}
\end{align}
と定めれば,問題3同様の連立一階微分方程式に帰着される.
後は同様に解けば良い.
その他の重要な手法
Symprectic Euler法
ここまで数学に寄った話が続いたので,物理学科らしい話題が絡む事項に触れたい.
解析力学のHamilton形式では,時間に依存する変数として座標$\boldsymbol q={}^t(q_1,q_2,...q_n)$とそれに共役な運動量$\boldsymbol p={}^t(p_1,p_2,...p_n)$の組を考える.
Hamiltonian$\mathcal H=\mathcal{H}(\boldsymbol q,\boldsymbol p)$に対し,正準方程式
\begin{align*}
\begin{cases}
\dfrac{d}{dt}q_i&=\dfrac{\partial}{\partial p_i}\mathcal H\\
\dfrac{d}{dt}p_i&=-\dfrac{\partial}{\partial q_i}\mathcal H
\end{cases}
\end{align*}
が運動方程式に対応する.
Hamilton形式で記述される力学系(Hamilton力学系)においては,Symplectic構造を保つことが知られている.
即ち,次の2次微分形式
$$\omega=\sum_{j=1}^ndp_j\wedge dq_j$$
が保存される.
単純な例として調和振動子を考える.(質量などは変数に入れ込むことにする)
$$\mathcal H(q,p)=\dfrac{1}{2}p^2+\dfrac{1}{2}q^2 $$
\begin{align*}
\begin{cases}
\dfrac{d}{dt}q&=p\\
\dfrac{d}{dt}p&=-q
\end{cases}
\end{align*}
この時,微分形式に対応するのは$(q,p)$が張る空間(位相空間)の上の$(q,p)$の描く軌跡の囲む面積である.(証明略)
これに対して陽的Euler法とRK4を用いると,漸化式は次のようになる.
陽的Euler法
$$
\begin{pmatrix}
q_{n+1}\\
p_{n+1}
\end{pmatrix}
=
\begin{pmatrix}
1&h\\
-h&1
\end{pmatrix}
\begin{pmatrix}
q_{n}\\
p_{n}
\end{pmatrix}$$
RK4
$$
\begin{pmatrix}
q_{n+1}\\
p_{n+1}
\end{pmatrix}
=
\begin{pmatrix}
1-\frac{1}{2}h^2+\frac{1}{24}h^4&h-\frac{1}{6}h^3\\
-h+\frac{1}{6}h^3&1-\frac{1}{2}h^2+\frac{1}{24}h^4
\end{pmatrix}
\begin{pmatrix}
q_{n}\\
p_{n}
\end{pmatrix}
$$
それぞれの係数行列式を求めると,陽的Euler法は$1+h^2>1$,RK4は$1-\frac{1}{72}^6+\frac{1}{576}h^8<1$(as$0< h\ll 1$).
係数行列式は位相空間の面積の拡大率に対応しているため,陽的Euler法では原点中心の円から離れていき,RK4では軌跡は原点に向けて収縮していく.
これを防ぐための計算スキームを考えたい.
Symplectic Euler法を次で定める.
$$
\begin{pmatrix}
q_{n+1}\\
p_{n+1}
\end{pmatrix}
=
\begin{pmatrix}
1&h\\
-h&1-h^2
\end{pmatrix}
\begin{pmatrix}
q_{n}\\
p_{n}
\end{pmatrix}$$
これは係数行列式が$1$より,位相空間の軌跡の囲む面積は保存されている.
Symplectic Euler法は,一般のHamiltonianにおいて陰解法になっていることが知られている.
また,Hamiltonianが時間をexplicitに含まない関数の関数の場合,$\mathcal H$は時間発展で変化しないが,この解法では$\mathcal H(q_n,p_n)$は定数にならない.
実装
ここではPythonを用いた実装を考える.
ここまでさまざまな手法を紹介してきたが,実用的には,RK4を用いるのが簡便かつ精度が期待できるため使いやすい.
筆者は微分方程式の解析を行う場合,まずRK4を選択することにし,他に適切な手法がある場合(方程式が解ける場合,Symprectic構造を保つ解法が採用できる場合など)はそれを用いることにしている.
実際の問題を考える場合は,関数の形がさまざまであるため,RK4による補完の部分をモジュール化しておいて書き換える,という運用をする.
# --- Runge-Kutta4 (RK4) 法 ---
def rk4_step(f, dt):
k1 = dt * df_dt(f)
k2 = dt * df_dt(f + 0.5 * k1)
k3 = dt * df_dt(f + 0.5 * k2)
k4 = dt * df_dt(f + k3)
f_new = f + (k1 + 2*k2 + 2*k3 + k4) / 6.0
return f_new
演算を行う前に$dt$と関数fを定義しておけば良い.
例えば,3体問題の数値解法なら,万有引力を用いることで,
def dP_dt(P):
r = P[:6].reshape((3, 2)) # 位置ベクトル r1, r2, r3
v = P[6:].reshape((3, 2)) # 速度ベクトル v1, v2, v3
r1, r2, r3 = r[0], r[1], r[2]
v1, v2, v3 = v[0], v[1], v[2]
# 距離の計算
r12_vec = r2 - r1
r13_vec = r3 - r1
r23_vec = r3 - r2
r12_norm = np.linalg.norm(r12_vec)
r13_norm = np.linalg.norm(r13_vec)
r23_norm = np.linalg.norm(r23_vec)
# 加速度の計算 (a = (G*m_j * r_ij) / |r_ij|^3)
a1 = G * m * (r12_vec / r12_norm**3 + r13_vec / r13_norm**3)
a2 = G * m * (-r12_vec / r12_norm**3 + r23_vec / r23_norm**3)
a3 = G * m * (-r13_vec / r13_norm**3 - r23_vec / r23_norm**3)
# dP/dt = [v1_x, v1_y, v2_x, v2_y, v3_x, v3_y, a1_x, a1_y, a2_x, a2_y, a3_x, a3_y]
dP = np.concatenate((v1, v2, v3, a1, a2, a3))
return dP
などと右辺の関数を定められるので,これをRK4のモジュールの$f$に代入すれば時間発展を数値的に求められる.
最後に
ここまでお読みいただきありがとうございました.
この記事は今年の春に受講していた講義"自然科学ゼミナール(数理科学)"において私がよく使う,もしくは重要だと感じた部分をまとめたものになります.
微分方程式が解けないため関数形こそわからないものの,解曲線が数値解法により導かれた問題に3体問題があります.
安定した軌道を持つ解として知られる舞踏解の図を示してこの記事を締めたいと思います.
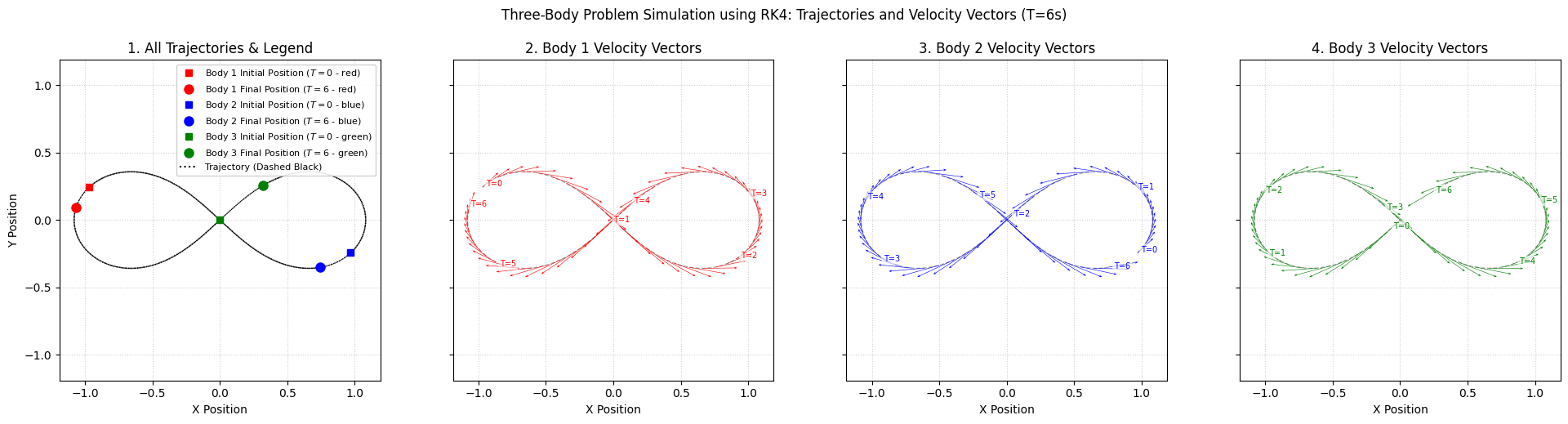舞踏解
