飛行機はなぜ飛ぶのか？～巷にあふれる説明を徹底的に深堀する～

飛行機はなぜ飛ぶのだろうか。巷にあふれている啓蒙書やインターネット上のページを開けば、様々な説明が出てくる。「揚力が発生するのは循環が生じるからだ」「翼の形状が膨らんでいるからだ」「作用・反作用の法則があるから」とにかく、多種多様な説明である。

　そう、多種多様すぎるのだ。説が乱立していて、一体どれが正しいのか分からない。揚力の説明は間違っていることが多いとは知っているものの、ではどれが正しいのかもよくわからない。かといって、流体力学の専門書を開いても数式のオンパレードで理解できる気がしない。

　この記事は、そんな貴方のための記事である。数式の記述は出来るだけ避け、巷にあふれている説を網羅的に取り上げた。本記事を最後まで読めば、今まであやふやだった揚力の仕組みが、明快に分かることだろう。

　また、本記事は揚力の仕組みを説明しなくてはならなくなった人に向けても書かれている。ぜひ、参考にして欲しい。

ポテンシャル理論による説明

　一つ目の説である。一般向けの書籍でポテンシャル理論を取り上げているものを私は見たことがない。理由は単純で、難しすぎるからだ。しかし、揚力の仕組みを本当の意味で説明するなら、この説明は避けて通れない。そもそも、これでしか説明できない事象も多いのだ。

説の内容

　巷に溢れている揚力関係の説明は、定性的なものがほとんどであるが、実際には揚力の大きさは定量的に求められる。

　複素関数論と写像等のテクニックを使えば、理想的な条件（完全流体・二次元翼、翼の三次元的要素を無視し、翼断面形のみから揚力を算出する）下で揚力を正確に計算できるのである。そして、それはどんな翼形であろうとも可能であることが数学的に示せる。

　例えば、平板翼（実は翼のふくらみが無くても揚力は発生するのだ！）の揚力係数（ここでは揚力の大きさを表す値だと思ってくれればいい。本当は違うが）は

$C_L=2\pi \text{sin}\alpha$

と求められる。ここで、$\alpha$は迎え角である。無論、他の翼形についても同様である。どんな翼形であっても、理論上は厳密に揚力の値を求められるのだ（※０A）（※０B）。

クッタ・ジューコフスキーの仮定

　あれで終わってもいいのだが、もう少し掘り下げておく。実はポテンシャル理論だけでは揚力の値を正確に定めることができない。空気の流れについて、複数の解が出てきてしまうのだ。

　これはなにも珍しいことではない。微分方程式の一般解で見られるように、解が一つに定まらないことは往々にしてある。

　ポテンシャル理論から得られる解は複数あるにしても、現実に存在する解は一つしかない。つまり、もっと条件が必要なのだ。

　具体的には、翼上面の流れと翼下面の流れが、後縁（翼の後ろの端点）で合流するという制約を課す。この制約のことをクッタ・ジューコフスキーの仮定という。

仮定が成り立つ理由

　なぜ、クッタ・ジューコフスキーの仮定が成り立つのかという疑問が真っ先に湧き上がってくるかと思う。

　残念ながら理由はない。そう仮定すると現実と上手く整合するから、前述のように仮定しているだけである。

仮定がない場合の非現実的な流れ

　一応理由っぽいものを説明しておく。ポテンシャル理論は完全流体という、粘り気が全くない理想的なものを想定している。空気に粘性がないと空気は抵抗を受けないから、大きな速度で移動できる。

　上記の仮定を用いなかったとすると、翼後縁では、翼下面の空気が、翼上面に回り込むような空気の流れとなる。このとき、空気は極めて大きな速度で移動しなければならない。車で例えるなら、時速300kmで急カーブを曲がるような無理のある流れである。
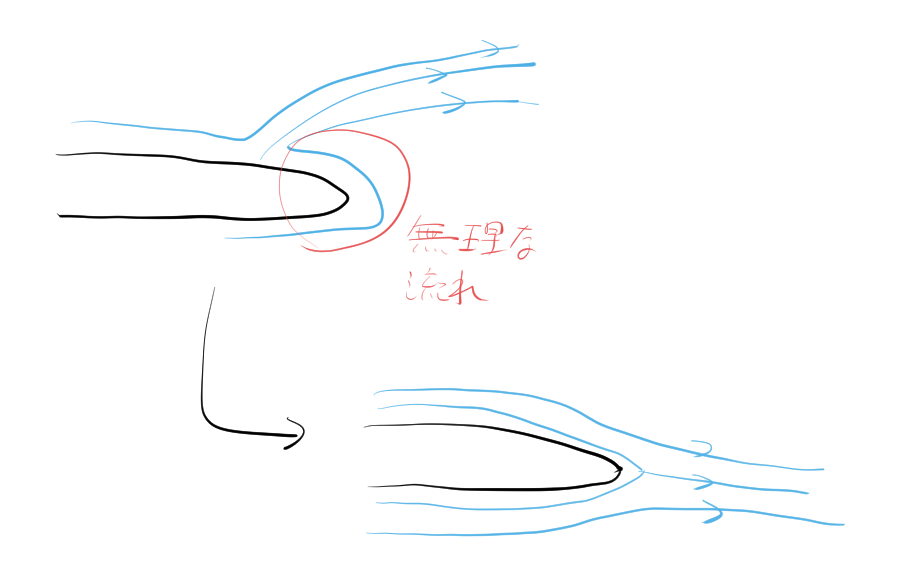クッタ・ジューコフスキーの仮定。同仮定は、翼上面空気と翼下面空気の、後縁での合流を要求する。 　

　（循環ゼロの場合）平板翼の後縁の速度をポテンシャル理論を用いて計算すると、無限大の速度になってしまう。そんな速度は実在しないだろう、というのは誰の目から見ても明らかである。

粘性の影響と出発渦、出発渦の視覚的証拠

　実際の空気には粘性が存在し、翼下面の空気は、翼上面に回り込むことなく、その場で渦を描いてしまう。これを出発渦という。クッタ・ジューコフスキーの仮定は、粘性の影響を考慮するために必要な仮定なのである。

　以下の動画は、出発渦の発生をシミュレーションしたものである。

https://www.youtube.com/watch?v=u8vyMHX9KNw

https://www.youtube.com/watch?v=bvV7-9wAXc0

　以下の動画は、実験で出発渦の発生を見たものである。動画時間0:30ごろから、後縁から反時計回りの渦が発生しているのが確認できる。また同時に翼下面の空気が、翼上面に引き込まれている様子も確認できる（※２）。

https://www.youtube.com/watch?v=XjpRMtkVAIc

クッタ・ジューコフスキーの定理

　クッタ・ジューコフスキーの仮定と関連して、クッタ・ジューコフスキーの定理を紹介しておこう。

　クッタ・ジューコフスキーの定理とは、流体中に置かれた物体が受ける揚力は、物体の循環$\mathrm{\Gamma }$と流体の速度$U$、流体の密度$\rho$にそれぞれ比例することを示した定理である。揚力を$F$とすれば

$$F=\rho U\mathrm{\Gamma }$$

である。

　流体の速度と流体の密度はいいだろう。物体の循環、そもそも循環とは何であろうか。

　循環とは、ここでは渦の強さを定量的に表す量とでも思ってくれればいい。

　なお、ここでいう「渦がある」とは、風車を流体の中に置いたとき、風車が回り出すかどうかを問うており、必ずしも視覚的に流体が回っている必要はないので注意が必要である。翼の話で言うと、もし翼上面と翼下面の流れの速さが異なるならば、そこには循環が存在する。頭の中である面を境にして、流速が違う流体の流れを考えてみたときに、その境に風車を置くとどうなるだろうか。風車は回り始めるはずだ。つまり、そこには循環が存在するのだ。

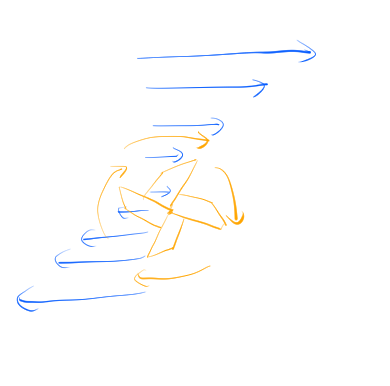渦のイメージ図。青線が流れを表している。青線の長さは流れの速さを示している。

　クッタ・ジューコフスキーの仮定については先ほど述べたが、実はこの仮定は循環と深い関係がある。というのも、この仮定は「翼後縁の流体の速度が無限大にならないように、循環の値を決める」とも言い換えられるからだ（※１）。

　なお、クッタ・ジューコフスキーの定理は、翼に限らずどんな形の物体でも成立する定理である。すなわち、「ある物体に循環がある」＝「ある物体に揚力がある」なのである。

説の正誤と説明の妥当性

　まずこの説明は正しい。というより、流体力学の中では最も正統派な説明である。もしこれが間違っているとしたら、一世紀以上に渡って積み上げられてきた航空力学の理論は、瞬く間に崩壊してしまう。我々は未知の力を頼って空を飛んでいたことになってしまう。そんなわけあるか。

　正しいがゆえに、理解するのは非常に困難である。本記事でも、ポテンシャル理論についてはほとんど説明していない。あれでは説明になっていない。この理論を厳密に説明するには

1. 微分・積分の知識

2. ベクトル解析

3. 複素関数論（複素関数の微分・複素関数の積分、ローラン展開など）

4. 流体力学に関する基礎知識

　等が必要である。仮に説明を受ける者がそれらの知識を有していたとしても、すべて説明しきるためには、1時間以上の時間を要する。航空講座等で、小学生にこれを教えるのは不可能である。航空講座は、飛行機や航空に興味を持ってもらうために開催するのであって、揚力理論の講義をする場所ではない。厳密性を追い求めて、小学生が興味を失って帰ってしまったら本末転倒である。

　よって、厳密性をある程度犠牲にして、揚力の発生機構を説明することになるのだ………が！　犠牲にしすぎて、間違った説明になってしまったり、間違いとは言えないまでも不適切な説明になってしまう例が散見される。

　実のところ、揚力の発生機構が正確に分かっていなくとも飛行機は操縦出来てしまうし（エアラインパイロットが間違った説明をしていたケースを見たことがある）、翼設計に携わるのであればどこかのタイミングで、ちゃんとした勉強をするはずであるから、実害は少ないといえる。とはいえ、揚力の発生機構は、飛行機の根幹原理であり、他の重要な事象（翼端失速、スピンの原理、後方乱気流の発生原理）と地続きで繋がっている。理解しておくに越したことはない。

循環理論による説明

　先ほど、出発渦の発生原理について述べた。ここを起点として、揚力の発生原理を述べたものが、循環理論である。説明の概要としては、次の通りである。

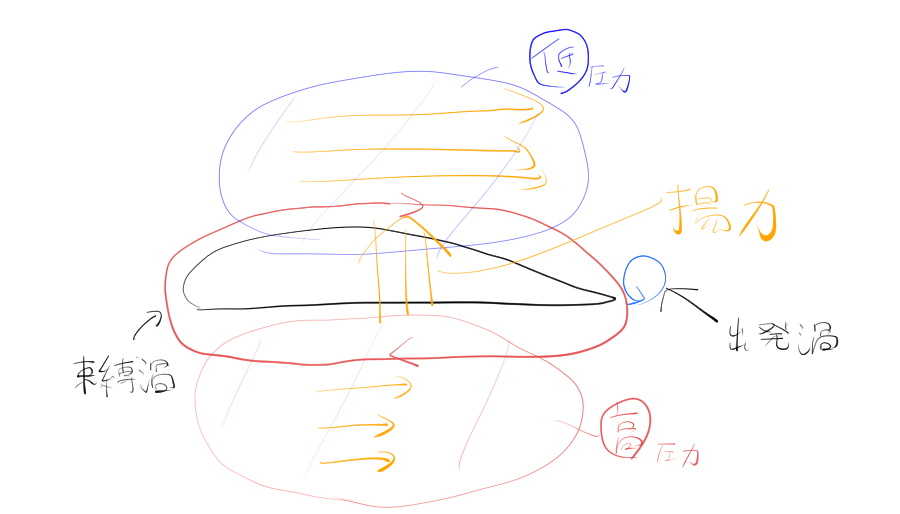出発渦と束縛渦

　ヘルムホルツの渦定理、ベルヌーイの定理が出てきた。一つ一つ説明していこう。

　ヘルムホルツの渦定理とは、時間変化によって循環の値が変わらないという定理である。ヘルムホルツの渦定理によって、最初に循環がなければ、以降もずっと循環がない流れ（渦無し流れ）となることが導ける。

　翼が動く前、当然循環は存在しない。前章で示したメカニズムで出発渦が発生した場合、ヘルムホルツの渦定理から、それを打ち消すような渦（循環）が発生しなければならない。それこそが、束縛渦である。

　束縛渦、出発渦について図示したものを以下に示す。
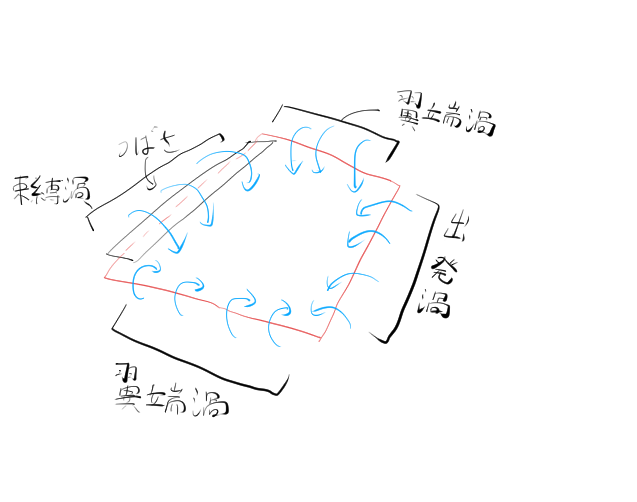出発渦、束縛渦、翼端渦の図示

　図で示したように、束縛渦、出発渦の他に、翼端渦という渦も発生する。翼端渦は翼の端で、翼下面から翼上面に空気が回り込むことによって発生する。

　翼端渦は、現実でも観測できる。下記の動画を参照のこと。

https://www.youtube.com/watch?v=IVl0vBijRro

　また翼端渦は、後方乱気流としても知られ、旅客機の墜落事故の要因にもなっている。例として、デルタ航空9570便墜落事故が挙げられる。こういった類の事故を防ぐため、飛行機と飛行機の間には必ず開けなければならない間隔が定められているほどである。渦は空想上のものではなく、現実に存在するのである。出発渦や翼端渦は、揚力の仕組みを説明するために導入された、仮想的なものと決して思ってはならない。

　ここでは詳しく説明しないが、翼端渦、出発渦、束縛渦は三つでセットである。出発渦だけ、翼端渦だけ存在することはありえない。もし、翼端渦が観測されるのであれば、出発渦や束縛渦も必ずセットで存在する。翼端渦や出発渦が観測される事実は、束縛渦の存在証明になっている。

　閑話休題。本題に戻ろう。

　ベルヌーイの定理とは、エネルギー保存則である。空気がある速度を持って運動している時、空気は運動エネルギーと、圧力エネルギーを持っている。これらの総和が常に保たれると言っているのだ。ベルヌーイ定理は、力学的エネルギー保存則に近い法則なのである。流速は物体の速さ、圧力は高さに例えられる。

　流速が大きくなると、運動エネルギーが大きくなる。ベルヌーイの定理が成り立つのであれば、総和は常に一定でなければならないから、圧力は小さくなる。逆に流速が小さくなれば、圧力は大きくなる。

　よくベルヌーイの定理は、コアンダ効果と混用される。自然に垂らした紙の上に、息を思い切り吹きかけると紙は浮き上がる。これをベルヌーイの定理で説明する文献がある（息を吹くと流速が大きくなって圧力が下がるから紙は下から押されて浮き上がる）が、誤りである。本来、コアンダ効果で説明すべき現象である（※３）。本例と同様に、ベルヌーイの定理ではなく、コアンダ効果で説明すべき事象として「水流に吸い寄せられるスプーン」がある。

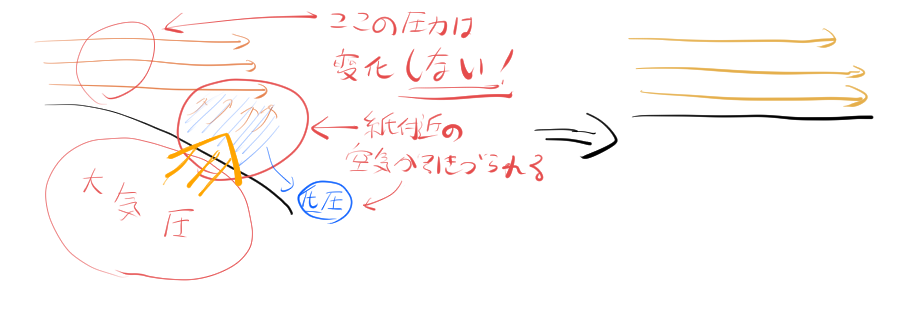コアンダ効果の説明。紙と息の間の空気が、息に引きずられることによって圧力が低下し、紙は圧力差によって浮き上がる。

説の正誤と説明の妥当性

　出発渦の発生する理由さえしっかり説明できれば、正確性と分かりやすさのバランスが取れたよい説明と言える。しかし、多くの者がその説明を飛ばしてしまう。いきなり翼に束縛渦が生ずると言ってしまうのだ。説明が長くなり、複雑になるのを嫌うからだろう。

　実際、クッタ・ジューコフスキーの定理より、循環があれば、どんな物体であっても揚力は発生する。だから、間違ったことを言っているわけではない。

　説明された方からすれば、あまりに天下り的過ぎて、理解しにくいと思われる。循環があったら揚力が発生するのは当たり前だろ、問題はどうして循環が発生するかだ、と思うに違いない。

　出発渦の発生する仕組みを説明するにあたっても問題がある。循環が発生する仕組みは何となく分かっても、これだけだと循環がどちらの向きに発生するかが分からない。循環がどちら回りなのかによって、揚力の正負が定まるため、無視できない話である（※７）。

　また、そもそも本当に翼下面の空気が翼上面に回り込むのかもよく分からない。直感的には明らかで色々理由付け（翼上面ではよどみ点が発生し、そこに向かうような流体の流れが発生するから、翼上面の圧力が、翼下面の圧力より低くなっているから）も出来るものの、正直あまり説明にはなっていない。

　まあ、それもそのはずで、これらの説明は、後付けなのである。理屈が先にあるのではなく、現象が先にあってそれをなぞって説明しているだけなのだ。だから、状況が変わったらどう現象が変わるのかという問いには答えられない。

　この問題点は、以降の説に共通して存在する問題である。予測を行うには、ポテンシャル理論に代表されるような「現実とできるだけ整合する仮定、ないし原理を定め、そこから理論を組み立てる。どうしても現実に沿わない部分については、理論を補正するか、あるいは仮定や原理に間違いがあるとみなして、抜本的な修正を加える」方法をとる必要がある。

　厳密性を犠牲にした弊害である。

形状で揚力発生を説明する

　翼上面の形状を理由にして、揚力の発生を説明する方式もある。一般的な飛行機の翼断面は、丸みを帯びている（この上への反りをキャンバーという）。

　この丸み付近では、流線曲率の定理より、圧力が低くなる。よって、翼下面との圧力差により揚力が生ずる。流線曲率の定理とは、空気がある角を曲がる時、空気の圧力は曲がり角中心方向に向かって圧力が低下し、その圧力勾配は、流速の二乗と曲がり具合（曲率）に比例するという定理である。

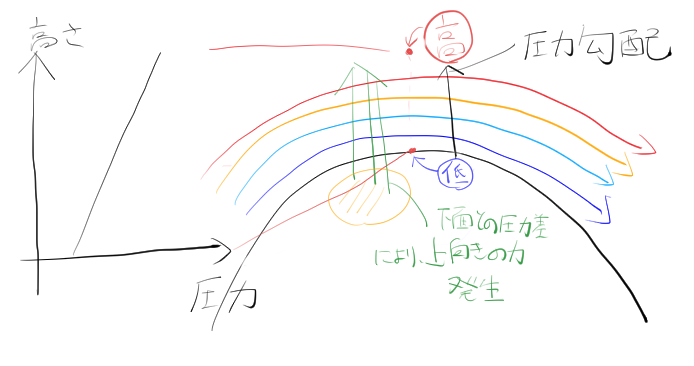曲がり角付近では圧力勾配が発生する

　もしくは、丸みによって空気の流れが加速され、翼上面の流れの方が、翼下面と比べ速くなるから揚力が発生するのだという説明もできる。

説の正誤と説明の妥当性

　初めに言っておくと、説明自体は間違っていない。実際、ポテンシャル理論等を用いて、同じ迎え角における平板翼と、キャンバー翼（翼を上に反らせたもの）の揚力係数を比較すると、キャンバー翼の方が大きい。下図に示すようなキャンバー翼の揚力係数は
$$C_L=2\pi \frac{\text{sin}(\alpha +\beta )}{\cos \beta }=2\pi \frac{\sin \alpha \cos \beta +\cos \alpha \sin \beta }{\cos \beta }=2\pi \sin \alpha +2\pi \cos \alpha \tan \beta$$

であり、これは平板翼の揚力係数$C_L=2\pi \text{sin}\alpha$より大きい。

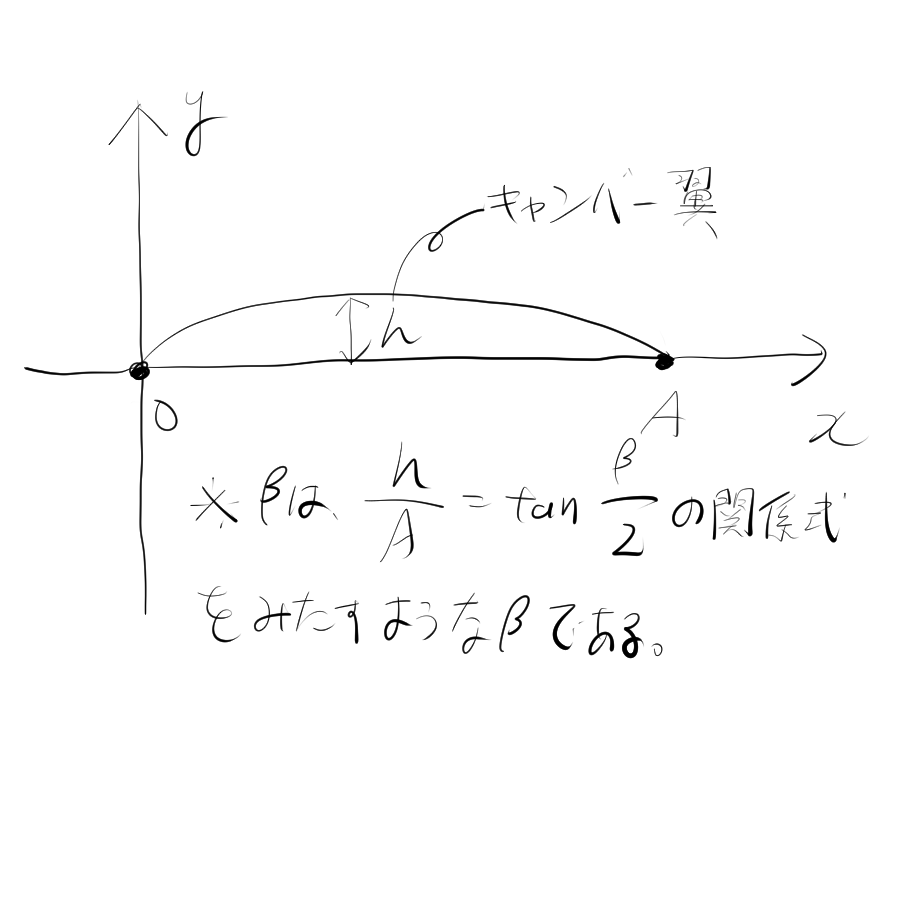キャンバー翼

そして、発生する現象に関する説明もあっている。丸みがある部分では、空気の流れが加速されるのは確かである。

　この説明は正しいが、不十分である。紙飛行機が飛ぶ理由を説明できない。また、背面飛行が出来る理由も説明できない。実際には、上図のような翼であっても、適切な迎え角を取れば背面飛行可能である。

　さらに、対称翼が飛べる理由も説明できない。対称翼でも、背面飛行と同様、迎え角をつけることによって、翼上面と翼下面に流れの非対称性が生まれ揚力が生ずる。揚力発生において、形状は重要ではあるが、それだけではない。

　参考までに、一般的な厚翼と、平板翼のシミュレーション結果を添付する。
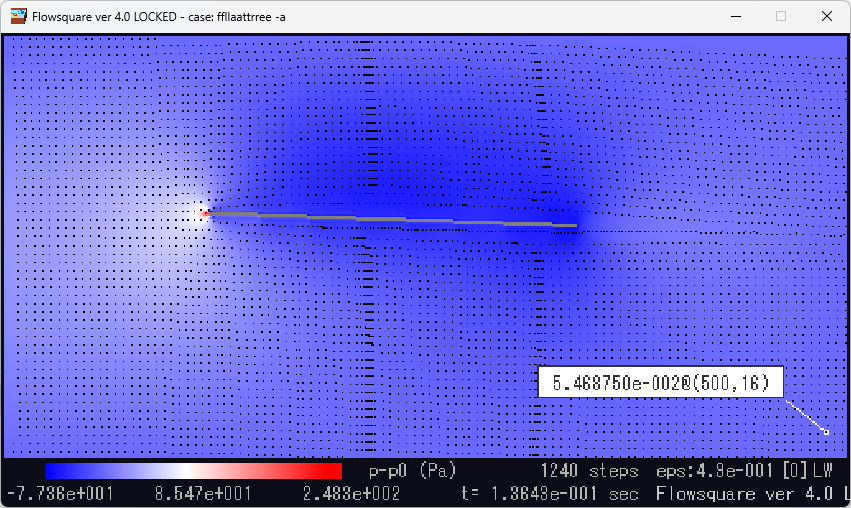平板翼の圧力分布シミュレーション。以下共通して青ければ青いほど値が小さいことを、赤ければ赤いほど値が大きいことを示している。また流れは左から右である。

平板翼の圧力分布に等圧線を加えたもの

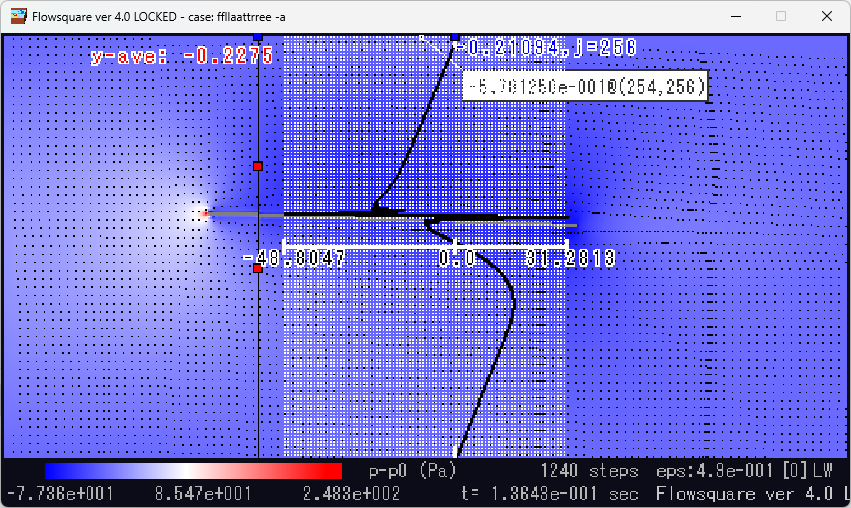平板翼前縁付近での縦方向圧力分布グラフ。上面は圧力が高く、下面は圧力が低くなっていることが分かる。

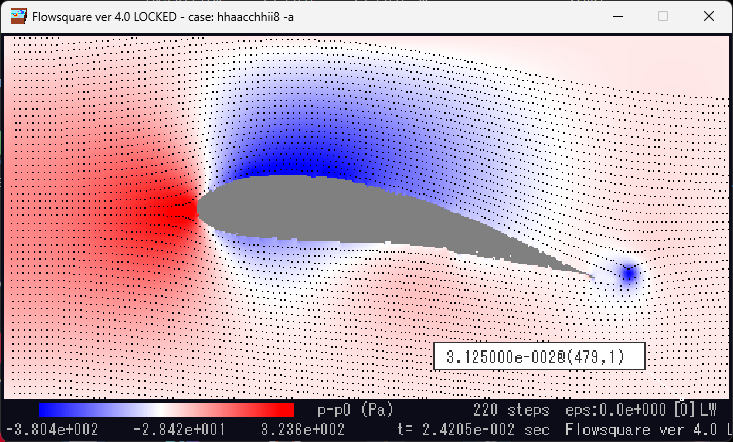一般的な厚翼の圧力分布シミュレーション。翼前端で急激に圧力が高くなり、その後翼上面を流れるにつれて圧力が急激に低下していることが分かる。翼後端には出発渦も見える。圧力差は平板翼より大きいことが視覚的に分かる（迎え角が違うため単純比較はできない）。

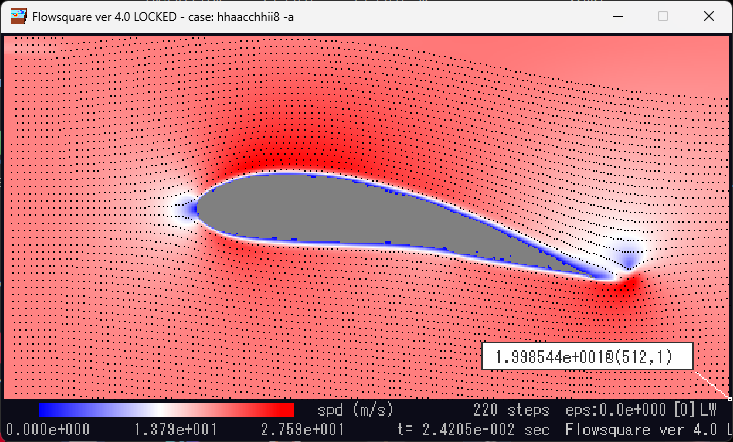一般的な厚翼の速度分布シミュレーション。翼前端で急激に減速し、その後、翼上面の曲がり角で急激に加速していることが分かる。

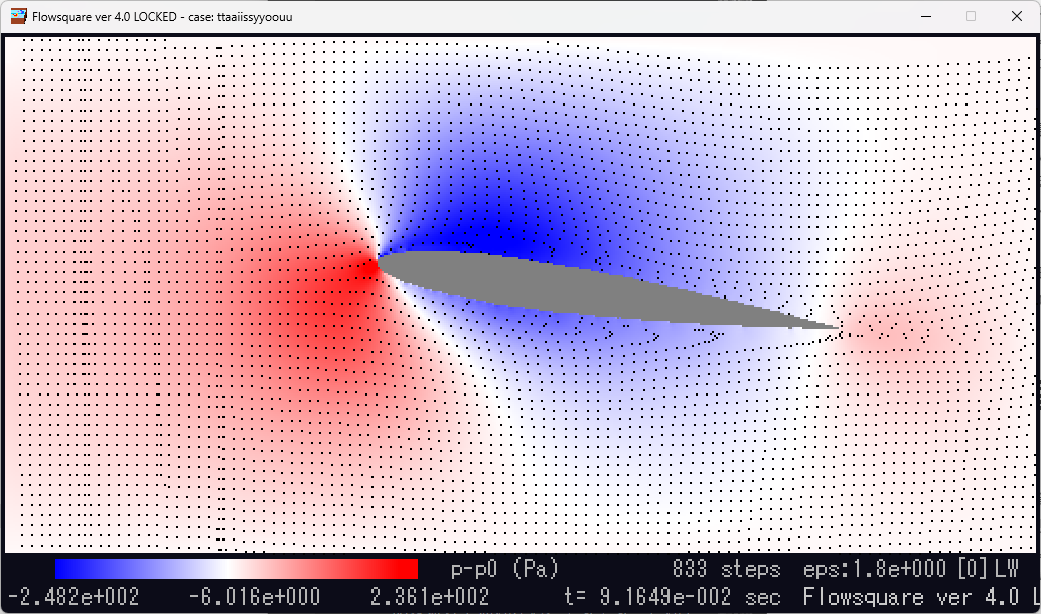対称翼の圧力分布シミュレーション。上向きの揚力が発生している。

空気の偏向による説明

　説明は間違ってはいない。正しい。しかし、あまりに大雑把すぎる。車で例えるなら、車の走る仕組みを「タイヤが回って地面を押すと、作用反作用の法則で地面がタイヤを押す。だから車は走るんだ」と説明するようなものである。ふつう、エンジンの仕組みから話すのではないだろうか？
　また誤解を生ずる可能性も高い。ここで言っている空気の偏向は、翼前面の形状による空気の偏向も含めているのだが、ロケットのアナロジーで翼後縁から出る空気の偏向だけを考慮すればよいと勘違いしかねない。

　あまり説明になっていないこと、誤解を生む可能性が高いことから、適切な説明とはいえないのではないだろうか。

等時間到着説

　よくある説明だが、これは誤りである。現実には上面と下面の空気が同時に着くことはない。

　下記の動画は、同着しない事実を実験で示したものである。

https://www.youtube.com/watch?v=UqBmdZ-BNig

　なお、等時間到着説が間違っていることをもって、ベルヌーイの定理も間違っているかのように説明する文献があるが、それは誤りである。ベルヌーイの定理は正しい。間違っているのは、流速が変化する原因を等時間到着説に求めている点だけである。

飛び石説（Skipping Stone Theory）

　飛行中、翼の下面に当たった空気は下に跳ね飛ばされる。その反作用として、翼には上向きの力が働く（＝揚力）という説明がなされることがある。
　この説明は、一部の特殊な場合を除いて、誤った説明である。理由をいくつか取り挙げよう。

1. 空気が下面に当たって跳ねるという考えは、粒子が個別に動くイメージを必要とする。しかし、一般的な航空機が置かれる状況では、空気はまとまって流れるため、その考えは誤りである（※６）。
2. たとえ粒子が当たると考えても、翼上面の空気を無視している。翼が下向きの揚力を生む場合や、スポイラーが役割を果たす理由を飛び石説では説明できない。

飛び石説が成立する条件

　先ほど、一部の特殊な場合を除いてと説明した。飛び石説は基本的に誤りだが、速度が非常に高く、密度が非常に低い場合においては、飛び石説でも十分に揚力を説明できることが知られている。大気圏に再突入するスペースシャトルが、この条件に当てはまる。
　無論、一般の旅客機では当てはまらないのは、言うまでもない。

最後に

揚力の発生機構まとめ

　長々と揚力の発生機構について述べてきた。最後に、正しい揚力の発生機構について、軽くまとめておこう。
　揚力の発生は、ポテンシャル理論で完全に予測できる。……もう少し正確に言うと、物体回りの完全流体の流れはポテンシャル理論で完全に予測できる。流れの速度場が予測出来る=流れの圧力場が予測できる=揚力の発生を予測できる、ことに他ならず、揚力はポテンシャル理論を用いて厳密に導き出すことが出来る。

　しかしポテンシャル理論だけでは流れが定まらない。粘性の影響を考慮していないからである。本文中で示した通り、クッタ・ジューコフスキーの条件を加えることで流れは一つに定まる。
　なぜそれで粘性の影響を考慮できるのか、という問いに応えたいところだが、実情を言えば単なる経験則にすぎない。実際、それで現実の揚力を正確に予測できるのだから、問題ないという考え方をする。
　クッタ・ジューコフスキーの条件がなぜ成立するのか追求するのは、磁石の同極がなぜ反発するのか聞いているようなものである。そこを追及していったところで、結局は「実在流体の粘性の性質がそういうものだから」にしかならない。

　以上は、揚力の発生原理というより、揚力の発生を導き出すための理論といった方が正しいと思われる。実験結果等から誰もが認める事実（原理）を定め、そこからいかなる事実（定理）が導出されるのか探っていくのである。────学問の根本原理であり、流体力学であれば、ナビエ・ストークス方程式や、連続の式、理論を構築するために置いた仮定等がそれに該当する。無論、クッタ・ジューコフスキーの条件も、である。
　揚力は、そういった原理を認めれば、必然的に導出され得るものだということを、ポテンシャル理論は述べているのである。

揚力発生機構の説明誤りの拡散について

　揚力発生機構のみならず、流体力学に関わる諸定理の誤解の拡散は、深刻である。石綿流体力学によれば、一般向け科学書139冊の半分近くに、流体力学の記述に関する明らかな誤りが見られるという。
　大学の一般教養で用いられている物理の教科書も、以上の誤りから逃れられていない。抽出した教科書40冊全体に見られた誤りの合計数は、実に39件に上る。著者は理学系学部の物理学科の教員であり、決して物理の素人ではない。

　どのような誤りが見られるのだろうか。石綿流体力学によると、一つは、等時間到着説を揚力発生機構として説明してしまっている、もう一つは、ベルヌーイの定理を単に「流速が速いと圧力が下がる定理」だと、説明してしまっているそうである。

　石綿流体力学は、書籍に見られる誤りの調査であった。では、インターネット上ではどうだろうか。本記事の筆者が軽く調査したところ、次のような内容が記載されていた。

1. 循環理論を用いた説明。
2. 翼上面と翼下面の形状が違うから、流速に差が生まれ、ベルヌーイの定理により揚力が発生するとする説明。
      1. 流速に差が生まれるのは事実で、ベルヌーイの定理により揚力が発生するのも事実である。が、ベルヌーイの定理を、流速が違うから圧力差が生ずる定理としか説明しておらず、誤解を招く可能性が高い。
3. 揚力の発生する仕組みは、複雑で難しいから、ここには書けないとする説明。
4. 揚力の発生する仕組みは諸説あって、未だよく分からないとする説明。
5. コアンダ効果によって、揚力は生み出されるとする説明。
6. 等時間到着説。
7. 空気の偏向による説明。

　割合としては二番が最も多く、他はほぼ同じくらいだった。特に五番・六番の説明は、某大手航空会社のホームページと同航空会社が行った講演であったものであり、事態の深刻さがうかがえる。
　誰か一人だけ間違っているのではなく、大多数の人が間違っているため、単に誤りを指摘するだけでは足らない。何らかの抜本的な対策が必要であり、それがこの問題を根深いものにしている。

　このような誤りを防ぐにはどうすればよいだろうか。
　一つ理解しなければならないのは、専門家は自身の専門分野についてしか詳しくない事実である。近年、学問の高度化が進み、分野も細分化されつつある。そのため、同じ電気工学の専門であっても、一人は送電理論に関する専門家、もう一人は電波に関する専門家、さらに別の人は通信工学の専門家、ということが往々にして起こる。発言者が単に大学の教授だからといって、発言をそのまま鵜呑みにしてはならない。通信工学について語っているその人は――――実は古文が専門の教授だった、なんて状況も考えられるからだ。
　航空分野についても同じである。パイロットは操縦の専門家であり、流体力学の専門家でない。整備士は、機体の整備が専門であり、飛行機の設計が専門ではない。もちろん、基礎教養として流体力学周りの知識は勉強しているだろうが、専門家に比べればどうしてもその知識量は劣る。

　広く広がってしまった誤りは流体力学分野に限らない。統計分野ではp値の誤用が氾濫していたり、情報分野では電子署名の説明が誤っていたりする。今回取り上げた揚力の誤りの場合は、実害はそこまで大きくない。しかし、医療系の分野でもし同じことが起きれば健康被害につながりかねない。実害のない誤りと実害のある誤りは明確に切り分けられず、地続きでつながっていると考えられる。「どうせ間違っていても困らない」と軽視するのではなく、真剣に向き合うことが必要なのではないかと、個人的には思う。

揚力発生機構の説明の提案

　揚力発生機構の説明は難しい。かといって、厳密性を削りすぎると誤解を生みかねない。説明の分かりやすさと厳密性のバランスを取った説明として、以下のようなものを考えてみた。

1. 揚力は、翼上面と翼下面の空気流れの非対称性によって生まれる。非対称性は、翼形状の違いや迎え角によって生まれる。
2. もちろん、非対称であればどんな流れでも揚力が生まれるわけではなく、条件がある。が、その辺りを議論するには時間が足らず、複雑であるため、説明は省略する。詳しくは循環理論等のキーワードで調べてみて欲しい。

各種定理（補足と厳密な説明）

　参考までに、本文中で登場した定理や用語の厳密な定義を紹介しておく。無理して理解する必要は全くない。「ちゃんとした理論があるんだな～」程度で構わない。私も理解させるつもりで書いていない。

任意翼形の定理

　本文中では、なぜ任意の翼断面で揚力が求められるのか説明を大幅に省略している。理由はあまりに難しすぎて、まともに解説したところで誰も理解できなさそうだから、なのだが……とはいえ、何も説明しないというのも、それはそれで問題かと思うので、大雑把に解説してみる。先に述べた通り、理解できなくても全く問題ない。むしろ、理解できないのが普通だ。

　大まかな発想としては、次の通りである。

1. 任意翼形を円に写すような写像を考える。そのような写像が必ず存在することは、リーマンの写像定理によって保証されている。
2. 任意翼形に流す、流れの向きと速さを決めれば、先ほど決めた写像によって、円柱周りに流す、流れの向きと速さも決まる。
3. ここで、円柱周りの流れというのは、容易に求められることが知られている。
4. 円柱周りの流れが求まれば、後は手順１で定めた写像の逆をすれば、任意翼形周りの流れが無事求まる。

循環

速度分布$\mathbf{v}(\mathbf{r},t)$の流体中に任意の閉曲線$C$をとる。このとき$\mathrm{\Gamma }$を閉曲線$C$に沿う循環という。

$$\mathrm{\Gamma }={\oint }_C(\mathbf{v}\cdot d\mathbf{s})$$

ヘルムホルツの渦定理

　ある一つの渦管を考える。保存力のもと、流体が完全流体であれば、流体運動が起こったとしても、その一つの渦管は一つの渦管として保たれ、また渦管の強さ（循環）も変化しない。これをヘルムホルツの渦定理という。

ベルヌーイの定理

流体の圧力を$p$、密度を$\rho$、速度を|$\mathbf{v}|=q$とする。流体の粘性は無視（完全流体）できるものとし、さらに流体は断熱的（外部との熱のやり取りを無視する）であるものとする。圧力関数$P$を

$$P(p)=\int \frac{dp}{\rho (p)}$$

と定義する。圧縮性流体も考慮しているため、$\rho$は一定でなく、$p$の関数になっていることに注意（圧力と密度がこの関係式で記述できるのは、等エントロピーの仮定があるからである）。

加えて、外力$\mathbf{K}$は保存力であるものとし、ポテンシャルを$\mathrm{\Omega }$とすると

$$\mathbf{K}=-\text{grad}\mathrm{\Omega }$$

以上の仮定の下、流線または渦線に沿って次の式が成り立つ。

$$P+\frac{1}{2}{q}^2+\mathrm{\Omega }=Const.$$

流線曲率の定理

ある角を回る流線に着目し、完全流体・定常・非圧縮流れ・外力無しであるものとする。その流線の法線ベクトル（内向きを正とする）を$\mathbf{n}$とし、圧力を$p$、曲率を$\kappa$、流体の速さを$q$、流体の密度を$\rho$とする。このとき、曲率中心に向かって圧力は降下しており、その降下率は流速の二乗と曲率、そして流体の密度に比例している。式で書くと次の通りである。

$$\frac{\partial p}{\partial \mathbf{n}}=-\kappa \rho q^2\mathbf{n}$$

以上の定理を、流線曲率の定理と言う。

クヌーセン数

　ある物体の平均自由行程を$\lambda$、代表長さを$L$とするときクヌーセン数$K$は、次の式で定義される。
$$K=\frac{\lambda }{L}$$

物体を流体として見なすためには、物体のクヌーセン数が十分小さい値でなければならない。
　なお、その物体が理想気体であり、なおかつ熱平衡状態であるとき、気体分子の速度分布は、マクスウェル・ボルツマン分布に従うから、平均自由行程$\lambda$は
$$\lambda =\frac{k_{B}T}{P\pi d^2\sqrt{2}}$$
となり、このときのクヌーセン数は
$$K=\frac{k_{B}T}{LP\pi d^2\sqrt{2}}$$
となる。ただし、$k_B$はボルツマン定数、$T$は気体の温度、$P$は圧力、$d$は分子直径である。上式から、クヌーセン数は圧力に反比例し、温度に比例することが分かる。

揚力シミュレーター

　NASAが、誰でも手軽に動かせる揚力シミュレーターを公開している。下のリンクから飛べる。流体シミュレーションほどの精密さはないが、揚力の仕組みを理解するには十分だろう。

https://www1.grc.nasa.gov/beginners-guide-to-aeronautics/foilsimstudent/

脚注

※０A：ここでいうポテンシャル理論とは、二次元ポテンシャル流に関する理論である。つまり、翼を断面形でしか見ておらず、三次元的な要素を一切無視している。
「じゃあ、三次元翼では必ずしも揚力を求められるとは限らないのか」と思った方、ちょっと待ってほしい。三次元翼であっても、非常に細かくスライスすれば、ほぼ平面と見なせるはずだ。各々の平面では、本文中で述べたように、厳密に揚力を求められる。これを足し合わせれば、結局三次元翼でも、揚力を厳密に求めることが出来る。
　この考えを発展させた理論が、揚力線理論と呼ばれる揚力計算方法である。

　念のため言っておくと、実際には他にも色々と考慮しなければいけないことがあり、現実の揚力値は単純な足し合わせでは求められない。上記の説明は、あくまでも概念的なものである。

※０B：ポテンシャル理論で求められるものは、揚力だけではない。すべての点における速度（速度分布）を求めることができる。後に述べるベルヌーイの定理により、速度分布が分かれば圧力分布も分かり、ここから揚力を求めることもできる。ポテンシャル理論はきわめて強力な理論なのである。

※１：ポテンシャル理論について勉強したことある人向けに補足しておく。平板翼において、クッタ・ジューコフスキーの仮定を用いても、前縁での速度無限大は解消されない。しかし、これを解消するのに循環を用いる必要はない。なぜなら、前縁で翼上面と下面の流れを合流させなくても、無限大速度は解消できるからである。流れを前縁で合流させる以外の解消方法として、前縁付近で渦を発生させるか、キャンバーが存在するものと考える。渦が発生すると考える場合、この渦によって翼全体の循環の値が変わるから、本来は計算に含めなければならない。しかし、通常無視する。

※２：よく「どうして飛行機が飛ぶかは、まだよくわかっていない」のように言われる。しかし、ここまで見てきてよくわかるように、全くそんなことはない。真っ赤な嘘である。もちろん、原子の粒一つ一つの動きを予測しているわけではないから、そういう意味では分かっているとは言えないかもしれない。だが「残りの0.0000001%が分かっていないから、我々は揚力について何も分かっていない」のように言ってしまうのは、あまりに不合理である。そもそも、あの言い回しだと勘で飛行機を設計しているかのように捉えられかねない。

※３
　コアンダ効果が飛行機の揚力に全く関係ないかというと……そういうわけでもない。高速のジェット気流を翼上面にあてて、大きな揚力を得ようとした飛行機が存在する。高速のジェット気流が翼上面を流れるとき、後に述べる流線曲率の定理から、翼上面付近に圧力勾配が発生し、これによる大きな揚力が発生する。普通、そんな高速のジェット気流が翼上面を流れようものなら剥離してしまいそうだが、コアンダ効果によって、気流は翼に沿うように流れる。コアンダ効果とは、噴流が物体表面に沿うように流れる現象を指すからだ。
　日本だと旧航空宇宙技術研究所（現JAXA航空技術部門）が実験機として開発した飛鳥と呼ばれるSTOL機がそれである。飛鳥が採用したこの方式は特に、アッパーサーフェスブローイング（Upper Surface Blowing,USB）と呼ばれる。
　以上の理由により、コアンダ効果は揚力発生に全く関係ないわけではない。しかし、コアンダ効果自体が揚力を生み出すわけではないのも事実である。
　紙の上に息を吹きかける実験を見て「あの紙を浮き上がらせる力で飛行機は飛んでいるのではないか」と勘違いしやすいがそうではない。一時的に生み出された低圧領域に紙が吸い寄せられているだけである。一度紙が吸い寄せられてしまえば以降は力がかからない。紙が持ち上がったままになるのは、何も力がかからなくなると、紙は下に落ちていこうとするためまたすき間ができ、コアンダ効果によって低圧領域が生まれ……のループによるものである。
　翼のような重く硬い物体だと、ジェット気流の方が物体に吸い寄せられる。翼を動かすよりも、ジェット気流を動かす方が圧倒的に楽（力が要らない）だからである。
　また、誤ったベルヌーイの定理の説明を聞いて「であれば、翼上面にジェット気流を吹かせればいいのではないか」と思う人もいるかもしれない。USB方式で解説した理由により、実際揚力は増すのだが、それはベルヌーイの定理によるものではないことは、抑えておかねばなるまい。

※４：流速が速くなったからといって、必ずしも圧力が低下しないことは簡単な実験で示せる。紙を真下に垂らし、片方の面に思い切り息を吹きかけるのである。もし、流速が大きくなると圧力が低下する（誤ったベルヌーイの定理）のであれば、息を吹きかけた側の圧力が下がり、紙は息を吹きかけた方に吸い寄せられるはずである。もちろん、実際にはそうはならない。この実験結果をもって、ベルヌーイの定理が誤っているとする文献があるが、そうではなくベルヌーイの定理の解釈を間違っているだけなので注意すること。

※５：ベルヌーイの定理は、完全流体でしか成り立たない。これをもって、揚力の説明にベルヌーイの定理は適用できないとする文献があるが、誤りである。確かに、実際の空気は粘性を持つが、粘性の影響は物体表面以外では無視できる。よって、翼回りの空気のほとんどは完全流体とみなしてよく、ベルヌーイの定理が適用できる。

※６：ここら辺の話は、物体がどのような仮定を満たせば流体として取り扱えるのか（流体力学の諸定理を適用できるのか）に関わってくる話である。これを判断する基準として、クヌーセン数と呼ばれる数が存在する。本記事では詳しく取り上げない。連続体やクヌーセン数といった言葉で調べれば、資料が出てくるはずだ。

※７：下向きの揚力（負の揚力）も存在する。下向きの揚力は、レーシングカーのダウンフォース等に応用されている。