格子の道と行列式について
ゲッセルとヴィアンノの補題について
今回は参考文献tenshoを元にして、格子の道と行列式との関係について手短に見て行きます。
まず次の事を認めましょう。
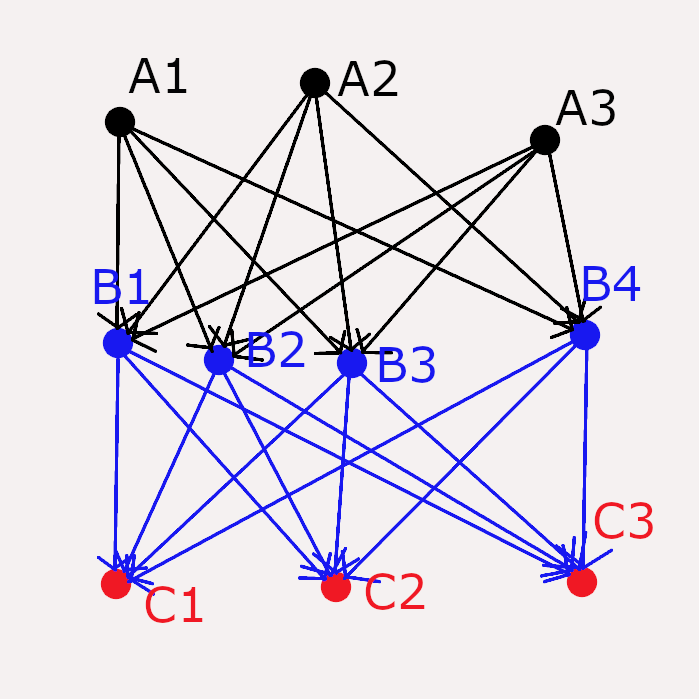
$M=\left(m_{ij}\right)$を$n\times n$行列とする。この時、$M$の行列式は次の様な重み付きの有効2部グラフを用いて表すことができる。
すなわち、頂点$A_{1},A_{2},...,A_{n}$を行列Mのそれぞれの行に対応させ、頂点$B_{1},B_{2},...,B_{n}$を行列Mのそれぞれの列に対応する様にし、図の様に$A_{i}$から$B_{j}$への矢印を描き、重み$m_{ij}$を与えた2部グラフを考えると次のように書ける。
\begin{equation}
\det\left(M\right)=\sum_{\sigma\in\mathfrak{S}_{n}}sgn\left(\sigma\right)w(P_{\sigma})
\end{equation}
ただし、この式の意味は次の様だ。
$\sigma\in\mathfrak{S}_{n}$を固定した時の$\mathcal{A}={A_{1},A_{2},...,A_{n}}$から$\mathcal{B}={B_{1},B_{2},...,B_{n}}$への頂点分離系の道を$P_{\sigma}$、また$w\left(P_{\sigma}\right)$は道$P_{\sigma}$の重みを表している。
![!FORMULA[15][1738373656][0]の場合](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2FNp4ZBZepAXdYShRLoP0t.png?alt=media)
$3\times 3$の場合
以下ゲッセルとヴィアンノの補題を証明するにあたって必要なものを定義します。
重み付き有効グラフ$G$の頂点$A$と頂点$B$を結ぶ道$P$が与えられているとき、道$P$の重み$w\left(P\right)$を次の様に定義する。
\begin{equation}
w\left(P\right)=\prod_{e\in P}w\left(e\right)
\end{equation}
重み付き有向グラフ$G=\left(V,E\right)$について、頂点の部分集合$\mathcal{A}=\{A_{1},A_{2},...,A_{n}\},\mathcal{B}=\{B_{1},B_{2},...,B_{n}\}$に対して、$n\times n$行列$M=\left(m_{ij}\right)$を次のように定義する。
\begin{equation}
m_{ij}=\sum_{P:A_{i}\rightarrow B_{j}}w\left(P\right)
\end{equation}
重み付き有向グラフ$G=\left(V,E\right)$について、頂点の部分集合$\mathcal{A}=\{A_{1},A_{2},...,A_{n}\},\mathcal{B}=\{B_{1},B_{2},...,B_{n}\}$に対して、$\mathcal{A}$から$\mathcal{B}$への道の系$\mathcal{P}_{\sigma}$は$P_{i}:A_{i}\rightarrow B_{\sigma\left(i\right)}\quad\left(i=1,2,...,n\right)$とからなるもので、$sign\left(\mathcal{P}_{\sigma}\right)=sign\left(\sigma\right)$と書く。また、道の系$\mathcal{P}_{\sigma}$の重み$w\left(\mathcal{P}\right)$を次のように書く。
\begin{equation}
w\left(\mathcal{P}_{\sigma}\right)=\prod_{i=1}^{n}w\left(P_{i}\right)
\end{equation}
サイクルの無い重み付き有向グラフ$G=\left(V,E\right)$について、頂点の部分集合$\mathcal{A}=\{A_{1},A_{2},...,A_{n}\},\mathcal{B}=\{B_{1},B_{2},...,B_{n}\}$に対して、$\mathcal{A}$から$\mathcal{B}$への道の系$\mathcal{P}_{\sigma}=\left(P_{1},P_{2},...,P_{n}\right)$が頂点分離であるとは、この道の系$P_{\sigma}$の任意の異なる二つの道を選んでも、それらの道が共通の頂点を持たない事である。
サイクルの無い重み付き有向グラフ$G=\left(V,E\right)$を考える。頂点の部分集合$\mathcal{A}=\{A_{1},A_{2},...,A_{n}\},\mathcal{B}=\{B_{1},B_{2},...,B_{n}\}$に対して、$M=\left(m_{ij}\right)$を$\mathcal{A}$から$\mathcal{B}$への道の行列とする。この時以下の式が成り立つ。
\begin{equation}
\det{M}=\sum_{\mathcal{P}\in\left(\mathcal{A}から\mathcal{B}への頂点分離な道の系\right)}sign\left(\mathcal{P}\right)w\left(\mathcal{P}\right)
\end{equation}
まず定義より、次の式が成り立つ。
\begin{eqnarray}
\det{M}&=&\sum_{\sigma\in \mathfrak{S}_{n}}sign\left(\sigma\right)\left(\sum_{P_{1}:A_{1}\rightarrow B_{\sigma\left(1\right)}}w\left(P_{1}\right)\right)\left(\sum_{P_2:A_{2}\rightarrow B_{\sigma\left(2\right)}}w\left(P_{2}\right)\right)\cdots\left(\sum_{P_{n}:A_{n}\rightarrow B_{\sigma\left(n\right)}}w\left(P_{n}\right)\right)\\
&=&
\sum_{\mathcal{P}\in\left(\mathcal{A}から\mathcal{B}への道の系\right)}sign\left(\sigma\right)\sum_{P_{1}:A_{1}\rightarrow B_{\sigma\left(1\right)}}\sum_{P_{2}:A_{2}\rightarrow B_{\sigma\left(2\right))}}\cdots \sum_{P_{n}:A_{n}\rightarrow B_{\sigma\left(n\right)}}w\left(P_{1}\right)w\left(P_{2}\right)\cdots w\left(P_{n}\right)\\
&=&
\sum_{\mathcal{P}\in\left(\mathcal{A}から\mathcal{B}への道の系\right)}sign\left(\mathcal{P}\right)w\left(\mathcal{P}\right)
\end{eqnarray}
示すべきことは以下の事である。それは$\mathcal{A}$から$\mathcal{B}$への道の系のうち頂点分離でない道の系を$\mathcal{N}$とすると、次の事が成り立つことである。\begin{equation}
\sum_{\mathcal{P}\in\mathcal{N}}sign\left(\mathcal{P}\right)w\left(\mathcal{P}\right)=0
\end{equation}
実際、$\mathcal{P}\in \mathcal{N}$を道$P_{i}:A_{i}\rightarrow B_{\sigma\left(i\right)}$を持つものとする。すると道$\mathcal{N}$の定義より、少なくとも一つ道$P_{j}$が存在して共通の頂点を持つ。
その共通の頂点で$A_{i}$から出発して一番最初に$P_{i}$と$P_{j}$の最初に共有する頂点を$X$とする。
次に、$\pi$を$\pi\mathcal{P}=\left(P_{1}^{'},P_{2}^{'},...,P_{i}^{'},...,P_{j}^{'},...,P_{n}^{'}\right)$の様に定める。ただし、$P_{i}^{'}\quad\left(i=1,2,...,n\right)$は次の様な道をなす。
\begin{eqnarray}
\left\{
\begin{array}{l}
\cdot k\neq i,jに対してはP_{k}^{'}=P_{k} \\
\cdot P_{i}^{'}は頂点A_{i}から頂点Xまでの経路はP_{i}、頂点Xから頂点B_{\sigma\left(j\right)}への経路はP_{j}に沿う様にとる。\\
\cdot P_{j}^{'}は頂点A_{j}から頂点Xまでの経路はP_{j}、頂点Xから頂点B_{\sigma\left(i\right)}への経路はP_{i}に沿う様にとる。
\end{array}
\right.
\end{eqnarray}
すると、以下の事が分かる。
まず、$\pi\left(\pi\mathcal{P}\right)=\mathcal{P}$。これは明らか。また、$\pi\mathcal{P}$と$\mathcal{P}$は同じ辺を使用しているので$w\left(\pi\mathcal{P}\right)=w\left(\mathcal{P}\right)$となる。
また、新しい置換$\sigma^{'}$は置換$\sigma$に$\left(i,j\right)$をかけたものなので、$sign\left(\pi\mathcal{P}\right)=-sign\left(\mathcal{P}\right)$となる。ゆえに、補題は示された。
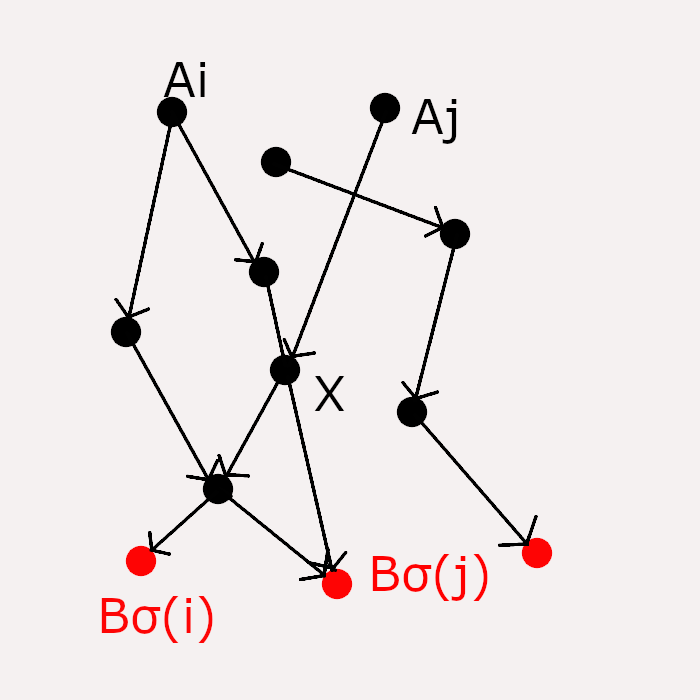ゲッセル・ヴィアンノの補題参考画像
応用1.ビネ-コーシーの公式の証明
$Pをr\times s$行列、$Q$を$s\times r$行列$(r \leq s)$であれば以下の式が成り立つ。
\begin{equation}
\det{PQ}=\sum_{\mathcal{Z}}\det{P_{\mathcal{Z}}}\det{Q_{\mathcal{Z}}}
\end{equation}
ただし、$\mathcal{Z}=\left(j_{1},j_{2},...,j_{r}\right)\in \mathbb{N}^{r}\quad \left(1\leq j_{1}\leq j_{2}\leq \cdots \leq j_{r}\leq s\right)$なる もの全体とし、$P_{\mathcal{Z}}$は$P$の$j_{1},j_{2},...,j_{r}$列を抜き出して作った$r\times r$行列。また、$Q_{\mathcal{Z}}$は$Q$の$j_{1},j_{2},...,j_{r}$行を抜き出した$r\times r$行列とした。
グラフ$G=\left(V,E\right)$を$\mathcal{A}=\{A_{1},A_{2},...,A_{r}\},\mathcal{B}=\{B_{1},B_{2},...,B_{s}\},\mathcal{C}=\{C_{1},C_{2},...,C_{r}\}$とし、
$E=\mathcal{A}\cap\mathcal{B}\cap\mathcal{C}$とする。また、$\mathcal{A}$と$mathcal{B}$の部分を見ると２部グラフ、また$\mathcal{B}$と$mathcal{C}$の部分を見たときも同様に２部グラフになる様に辺の集合$V$を構成する。
また、各辺の重みは$w\left(A_{i}\rightarrow B_{j}\right)=p_{ij},w\left(B_{j}\rightarrow C_{k}\right)=q_{jk}$となる様にとると、$\mathcal{A}$から$\mathcal{C}$への道の$\left(i,k\right)$行列$M$の成分$m_{ik}$はグラフの構成の仕方から$m_{ik}=\sum_{j=1}^{s}p_{ij}q_{jk}$。
また、繋いだグラフにおける$\mathcal{A}$から$\mathcal{C}$への頂点分離の道の系はそれぞれ$\mathcal{A}$から$\mathcal{B}$への頂点分離の道の系と$\mathcal{B}$から$\mathcal{C}$への頂点分離の道の系の対なので、下記の式が導かれるので証明が完了する。
\begin{eqnarray}
\det{M}&=&\det{PQ}\\
&=&\sum_{\mathcal{Z}}sign\left(\sigma\tau\right)p_{i\sigma\left(j\right)}q_{\sigma\left(j\right)k}\\
&=&\sum_{\mathcal{Z}}sign\left(\sigma\right)p_{i\sigma\left(j\right)}sign\left(\tau\right)q_{\sigma\left(j\right)k}\\
&=&\sum_{\mathcal{Z}}\det{P}\det{Q}
\end{eqnarray}
ビネ-コーシの公式
応用2.行列式の計算
$a_{1}\lt a_{2}\lt \cdots \lt a_{n}$と$b_{1}\lt b_{2}\lt \cdots \lt b_{n}$を自然数の作る２つの集合とする。今$m_{ij}$が２項係数${}_{a_{i}}C_{b_{j}}$である様な行列$M=\left(m_{ij}\right)$の行列式を計算せよ。
下記図の様な格子を考える。
また点$A_{i}$の座標を$\left(0,-a_{i}\right)$、点$B_{j}$の座標を$\left(b_{j},-b_{j}\right)$の様に設定する。
この格子上で点$A_{i}$から$B_{j}$まで最短で移動する(上あるいは右に移動するのみが許される)道の数は簡単な考察から${}_{a_{i}}C_{b_{j}}$．ゆえに与えられた行列$M$はすべての辺の重みが1であり、すべての辺の向きが右向きあるいは上向きの有向グラフで、$\mathcal{A}=\{A_{1},A_{2},...,A_{n}\}$から$\mathcal{B}=\{B_{1},B_{2},...,B_{n}\}$への道の行列になる。
また、$\mathcal{A}$から$\mathcal{B}$への任意の頂点分離の道の系$\mathcal{P}$はすべての$i$に対して、$P_{i}:A_{i}\rightarrow B_{i}$である道からなっていないといけないことが分かる。
ゆえに、以下の結論を得る。
\begin{equation}
\det{M}=\#\{\mathcal{A}から\mathcal{B}への頂点分離の道の系\}
\end{equation}
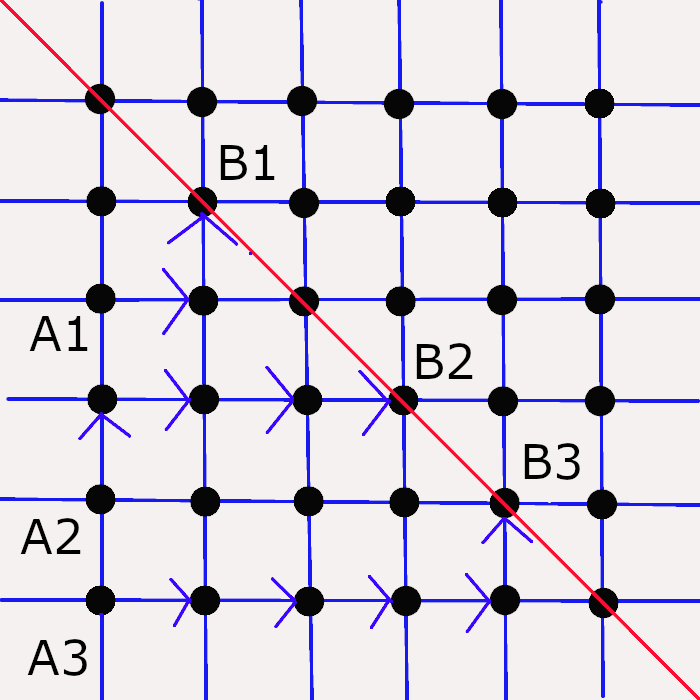ゲッセルとヴィアンノの補題応用
参考文献
この記事を高評価した人
この記事に送られたバッジ
投稿者
