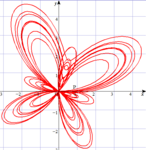
楕円曲線y^2=x^3+x-1の有理点の偏在

楕円曲線$y^2=x^3+x-1$の有理点を生成元から100個プロットすると偏在的に分布することについて

元ポスト：
https://twitter.com/fmathsecond/status/1821230082649940310

見かけた考察：
https://twitter.com/algebraic_ghost/status/1821752943760302450

私のコメント：
https://twitter.com/icqk3/status/1822234659918426550

Xのポストは流れてしまうのでここに書き留めておこうと思った。

端的に、生成元である(1,1)が、19等分点にとても近いということのようだった。

正則な微分形式δをとりあえず1つ、例えば$δ=dx/y=2dy/(3x^2+1)$ととって 「無限遠点から点Pまでδを線積分する」という数値計算で観察できた。