ある積分を解く

$$\int_{0}^{\infty}\frac{\log x}{x^2+1}dx$$

\begin{align} I&=\int_{0}^{\infty}\frac{\log x}{x^2+1}dx \\&=\int_{0}^{1}\frac{\log x}{x^2+1}dx+ \int_{1}^{\infty}\frac{\log x}{x^2+1}dx \\&=\int_{0}^{1}\frac{\log x}{x^2+1}dx+ \int_{1}^{0}\frac{\log\frac{1}{t}} {\left(\frac{1}{t}\right)^2+1} \left(-\frac{1}{t^2}\right)dt \qquad\left(x\mapsto\frac{1}{t}(t>0)\right) \\&=\int_{0}^{1}\frac{\log x}{x^2+1}- \int_{0}^{1}\frac{\log t}{t^2+1}dt \\&=0 \end{align}

$$\int_{a}^{\frac{1}{a}}\frac{f(x)}{x^2+1}dx =\int_{a}^{\frac{1}{a}} \frac{f\left(\frac{1}{x}\right)}{x^2+1}dx$$
$$\int_{0}^{\infty}\frac{f(x)}{x^2+1}dx= \int_{0}^{1}\frac{f(x)+f\left(\frac{1}{x}\right)}{x^2+1}dx$$

$$I=\int_{0}^{\infty}\frac{\log x}{x^2+1}dx$$
$$f(z)=\frac{\log x}{x^2+1}$$
として計算していく、②ではこの$f(z)$を変えて計算する。
後に使うので$f(-z)$を計算する。
\begin{align} f(-z)&=\frac{\log z+\pi i}{z^2+1} \\&=f(z)+\frac{\pi i}{z^2+1} \end{align}
次のような積分経路で積分する。
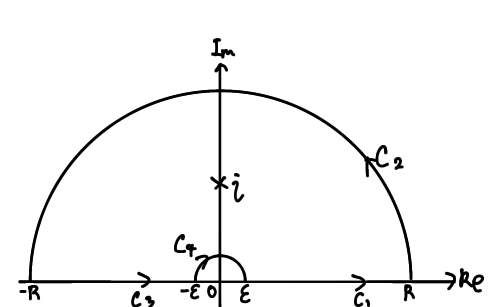考える積分経路
0を避けている理由は、$\log0$は未定義で考えられないから
一周した経路を$C$とする。
$C_2$と$C_4$は絶対値による評価で0になる。(やってみてね)
あとは$C_1とC_3$と$C$を計算すればいいことになる。
それぞれ計算していく。
\begin{align} \int_{C_1}&=\int_{ε}^{R}f(x)dx \\&=I\qquad(ε\to0\quad R\to\infty) \end{align}
\begin{align} \int_{C_3}&=\int_{-R}^{-\ipusiron}f(x)dx \\&=\int_{\ipusiron}^{R}f(-x)dx \\&=\int_{\ipusiron}^{R}f(x)dx+ \int_{\ipusiron}^{R}\frac{i\pi}{x^2+1}dx \\&=I+\frac{\pi^2}{2}i \qquad(\ipusiron\to0\quad R\to\infty) \end{align}
\begin{align} \oint_{C}&=2\pi i\underset{z=i}{\mathrm{Res}}f(z) \\&=2\pi i\lim_{z\to i}\frac{(z-i)\log z}{(z+i)(z-i)} \\&=\frac{\pi^2}{2}i \end{align}
$$I+I+\frac{\pi^2}{2}i=\frac{\pi^2}{2}i$$
$$I=0$$

$$I=\int_{0}^{\infty}\frac{\log^2x}{x^2+1}dx$$
この積分を計算していくと、求めたい1乗の積分がでできます。
$$f(z)=\frac{\log^2z}{z^2+1}$$
として計算します。
あとあと使うので$f(-z)$を計算します。
\begin{align} f(-z)&=\frac{(\log z+\pi i)^2}{z^2+1} \\&=f(z)+\frac{2\pi i\log z}{z^2+1}- \frac{\pi^2}{z^2+1} \end{align}
先ほどと同じ経路で積分していきます。
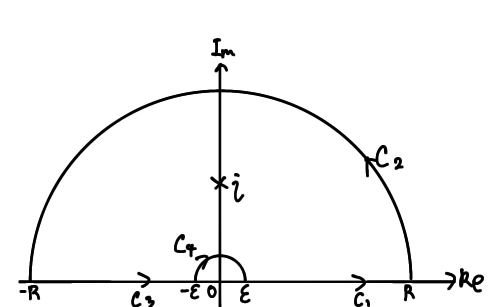積分経路
一周した経路を$C$とします。
$C_2$と$C_4$は絶対値で評価することで0になります。(やってみてね)
あとは$C_1$と$C_3$と$C$を求めていきます。
\begin{align} \int_{C_1}&=\int_{\ipusiron}^{R}f(x)dx \\&=I\qquad(\ipusiron\to0\quad R\to\infty) \end{align}
\begin{align} \int_{C_3}&=\int_{-R}^{-\ipusiron}f(x)dx \\&=\int_{\ipusiron}^{R}f(-x)dx \\&=\int_{\ipusiron}^{R}f(x)dx+ 2\pi i\int_{\ipusiron}^{R}\frac{\log x}{x^2+1}dx- \pi^2\int_{\ipusiron}^{R}\frac{dx}{x^2+1} \\&=I+2\pi i \int_{\ipusiron}^{R}\frac{\log x}{x^2+1}dx -\frac{\pi^3}{2} \qquad(\ipusiron\to0\quad R\to\infty) \end{align}
\begin{align} \oint_C&=2\pi i\underset{z=i}{\mathrm{Res}}f(z) \\&=2\pi i \lim_{z\to i}\frac{(z-i)\log^2z}{(z+i)(z-i)} \\&=-\frac{\pi^3}{4} \end{align}
$$I+I+2\pi i\int_{0}^{\infty} \frac{\log x}{x^2+1}dx-\frac{\pi^3}{2} =-\frac{\pi^3}{4}$$
$$I=\frac{\pi^3}{8}$$
虚部と実部を比較して、
$$I=\frac{\pi^3}{8}$$
$$\int_{0}^{\infty}\frac{\log x}{x^2+1}dx=0$$