凸集合と基本性質

凸解析学,凸集合

673

凸集合の定義と基本性質

この記事では凸解析学の中でも、基礎となる凸集合の定義から記載していきます。

はじめに

凸集合について、定義や基本性質などを図を交えてまとめていきます。

凸集合

convex,cone

集合$C$が$convex$（凸集合）である
$\Leftrightarrow \forall x,y \in C, \lambdarange に対して \convex{x}{y} \in C をみたす。$

集合$C$が$cone$（錐）である
$\Leftrightarrow x \in C,\lambda \geq 0 に対して \lambda x \in C をみたす。$

集合$C$がconvex（凸）、cone（錐）であるという定義は上のとおりです。凸集合というのは、ある集合からどのような2点を選んでも、その2点間のすべての点が集合に含まれているということになります。錐であるというのは、集合から選んだ点と原点を結んだ半直線（原点を始点とする）を考え、その半直線が集合に含まれていることをいいます。またconvex（凸）でもcone（錐）でもある集合をconvex coneといいます。定義から空集合はconvex（凸集合）とみなされます。

平面で図示した例

集合$C$は橙色の部分で示し、原点を$O$としています。

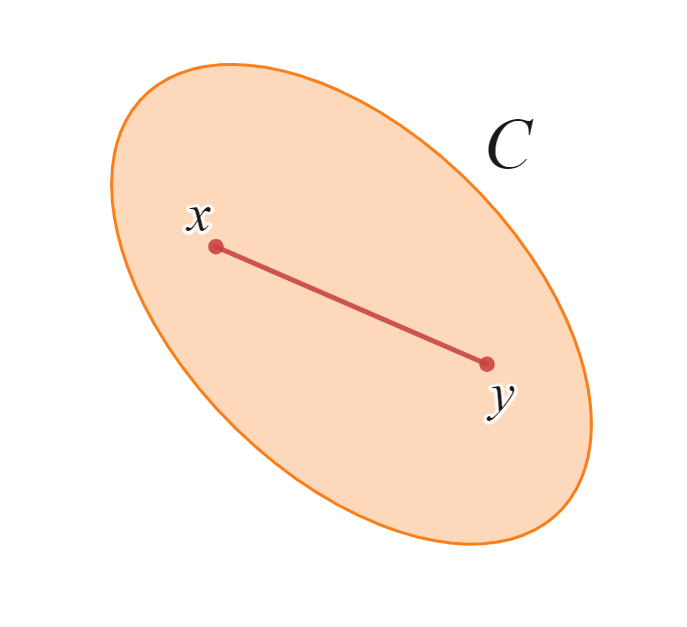convex set（凸集合）

2点$x,y$を集合$C$内のどこに移動させても、2点を結ぶ線分（赤色）は$C$の外にはみ出ることはありません。この線分が$\lambda x+ (1- \lambda )y \ (0 \leq \lambda \leq 1)$です。

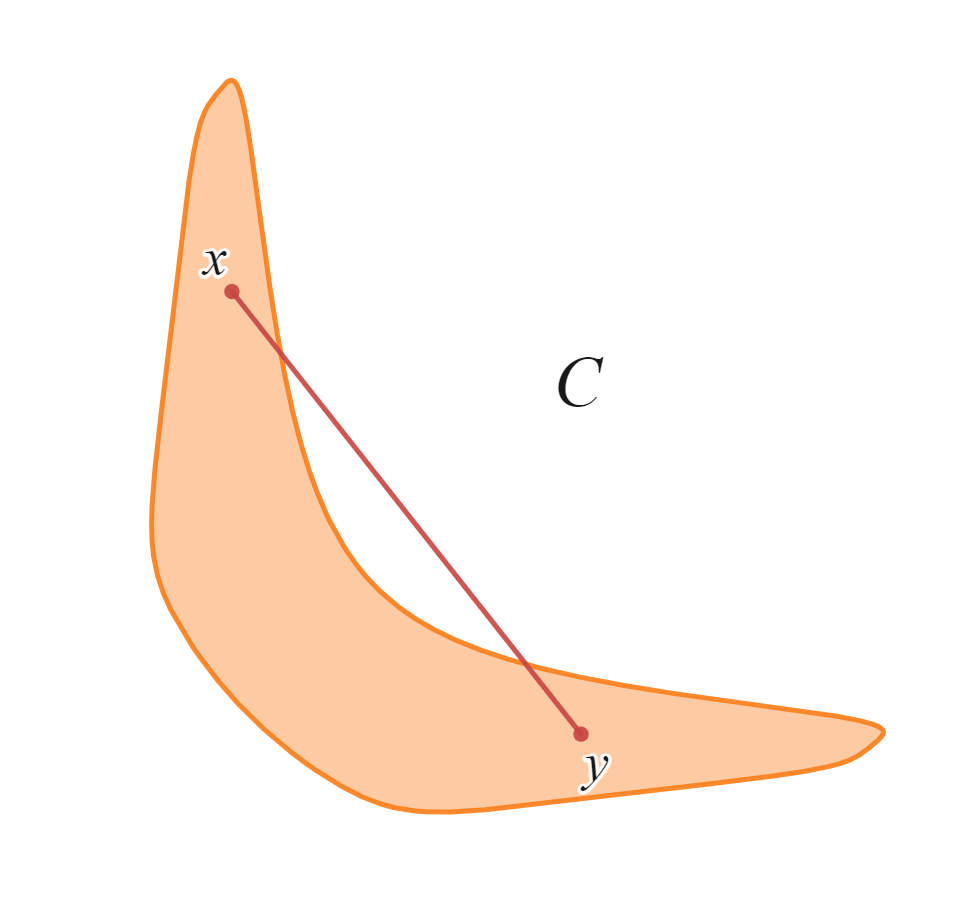non-convex set（凸でない集合）

2点$x,y$を結ぶ線分が$C$に含まれるように選ぶこともできますが、この図においては線分が$C$からはみ出る部分ができてしまいます。なので凸集合ではありません。

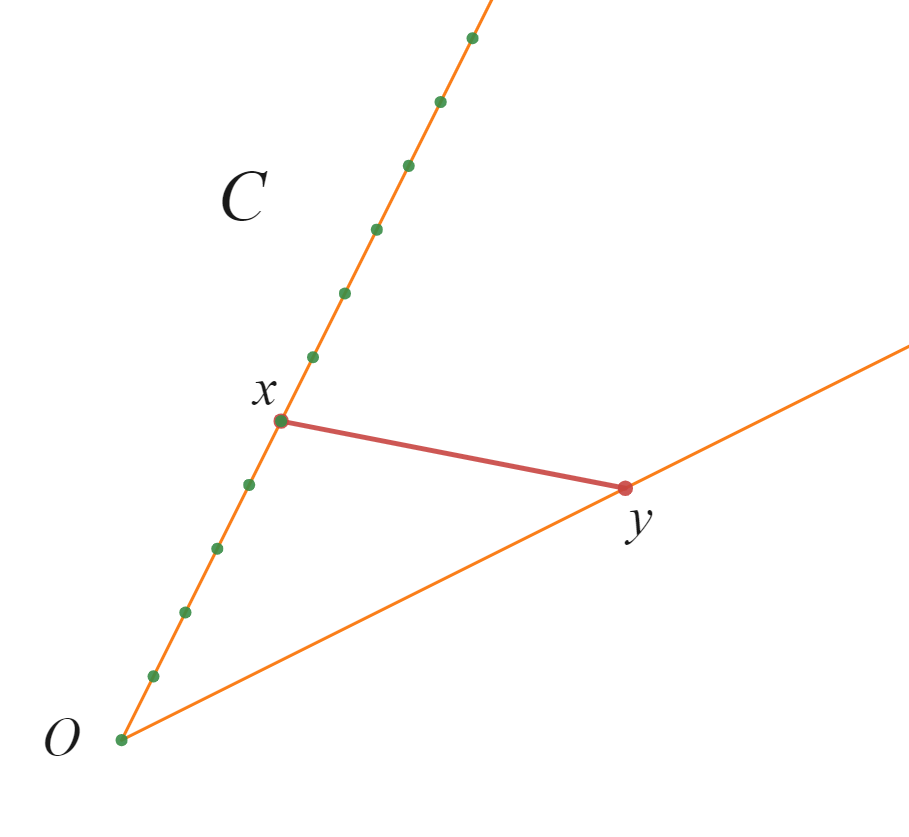cone（錐）

点$x$を正の実数倍した点、つまり$\lambda x \ (\lambda \geq 0)$となる点を緑色で示しています。これらのすべての点が$C$に含まれ、点$y$でも同様に考えることができるのでcone（錐）といえます。しかし点$x,y$を結ぶ線分は$C$からはみ出ているのでconvex（凸）ではありません。

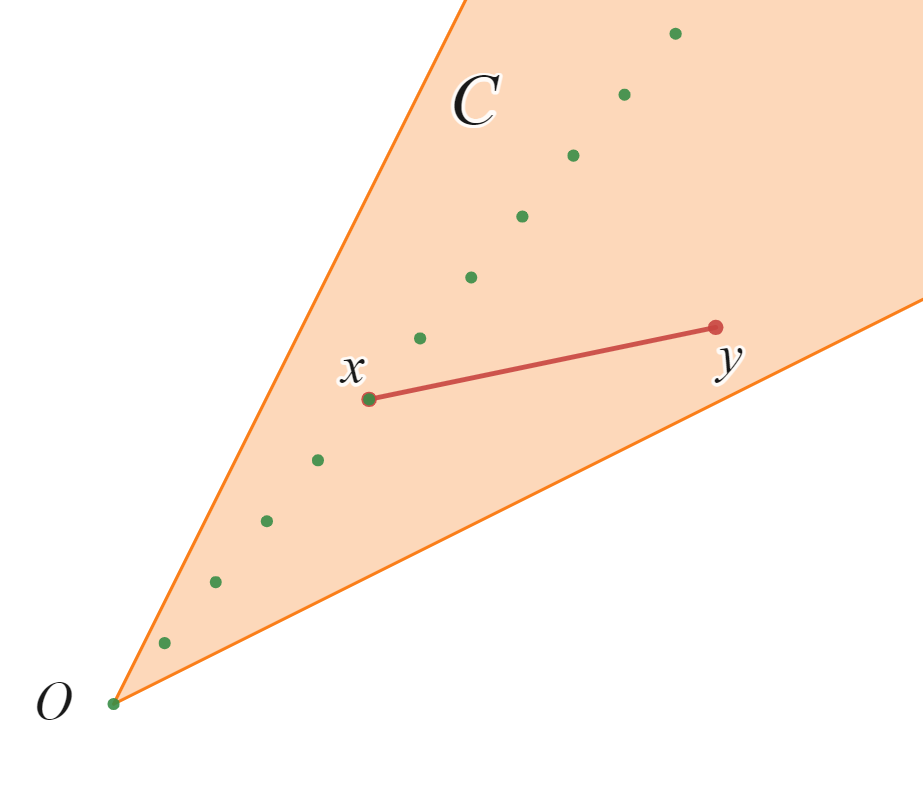convex cone（凸錐）

$\lambda x \ (\lambda \geq 0)$が$C$に含まれていて、点$x,y$を結ぶ線分も$C$に含まれているので、convex（凸）でもありcone（錐）でもある集合です。

凸集合に関するの演習問題

$$C:cone（錐）について、次が成り立つ。$$
$$C:convex（凸） \Leftrightarrow \forall x,y \in C, x+y \in C。$$

＜証明の考え方＞
$$(\Rightarrow)について。$$
$$x+y = 2(\frac{1}{2} x + \frac{1}{2} y) であることに着目する。$$

$$(\Leftarrow)について。$$
$$\convex{x}{y} を示したいので、まず \lambdax{x}, \lambday{y} \in C を示す。$$

$$(\Rightarrow)を示す。$$
$$C:convexより、\forall x,y \in C, \lambdarange に対して、\convex{x}{y} \in Cである。$$
$$\lambda = \frac{1}{2}とすると\frac{1}{2} x + \frac{1}{2} y \in Cとなる。$$
$$C:coneより、2(\frac{1}{2} x + \frac{1}{2} y) \in Cである。$$
$$すなわち、x + y \in C となり(\Rightarrow)が示せた。$$

$$(\Leftarrow)を示す。$$
$$C:coneより、\forall x,y \in C, \lambdarange に対して、$$
$$\lambdax{x}, \lambday{y} \in Cである。$$
$$すると条件より、\convex{x}{y} \in Cとなる。$$
$$よって、C:convexを示せた。$$

この問題を図で確認してみることにします。

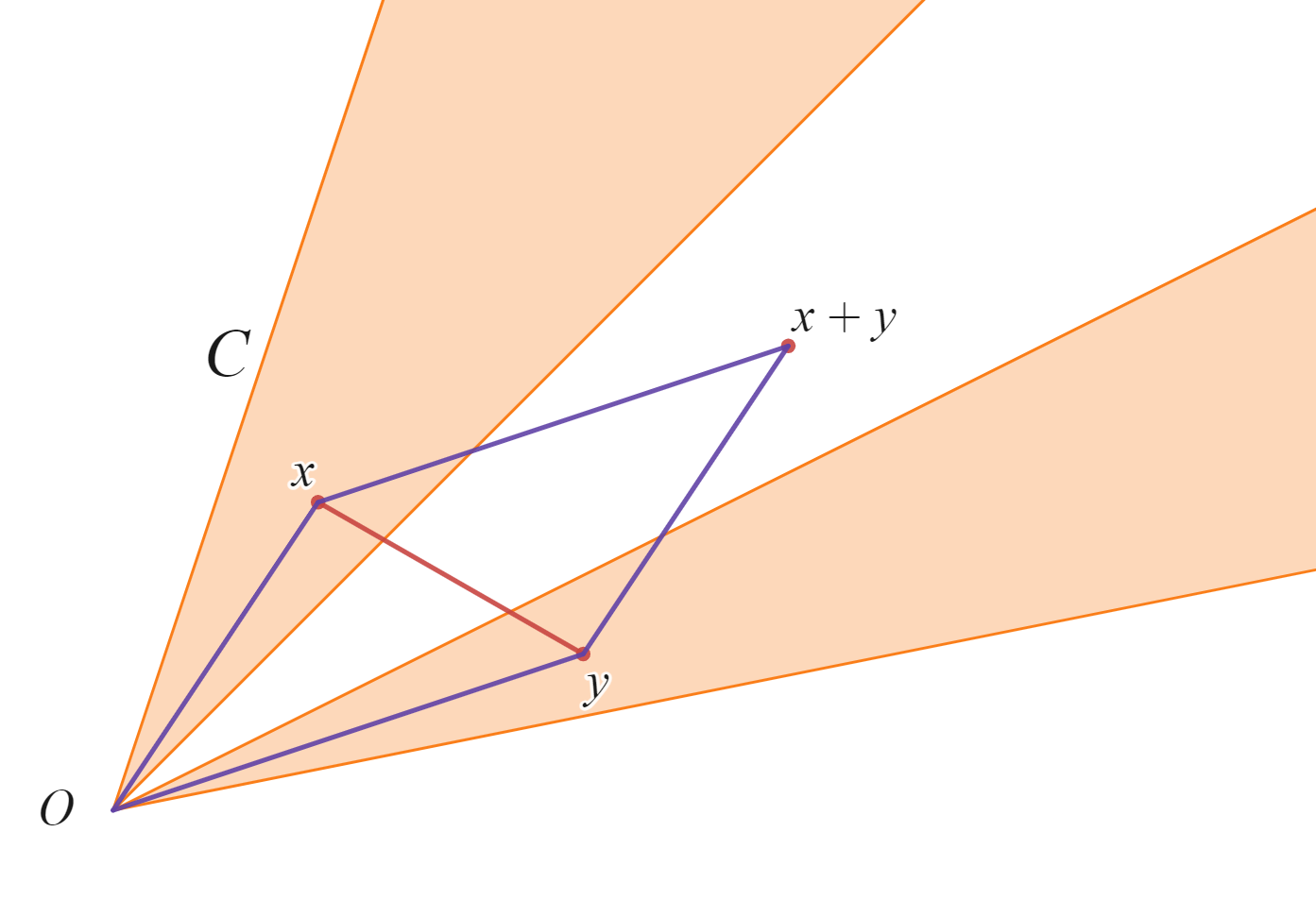cone, non convex（凸でない錐）

上の図では$x,y \in C$の凸結合の一部が集合$C$からはみ出ているのでconvexではありません。またこの図のように$x,y$をおくと、$x+y$も集合$C$に含まれていません。$x+y \in C$となるようにうまく$x,y$を取ることもできますが、任意の点でそうはいきません。

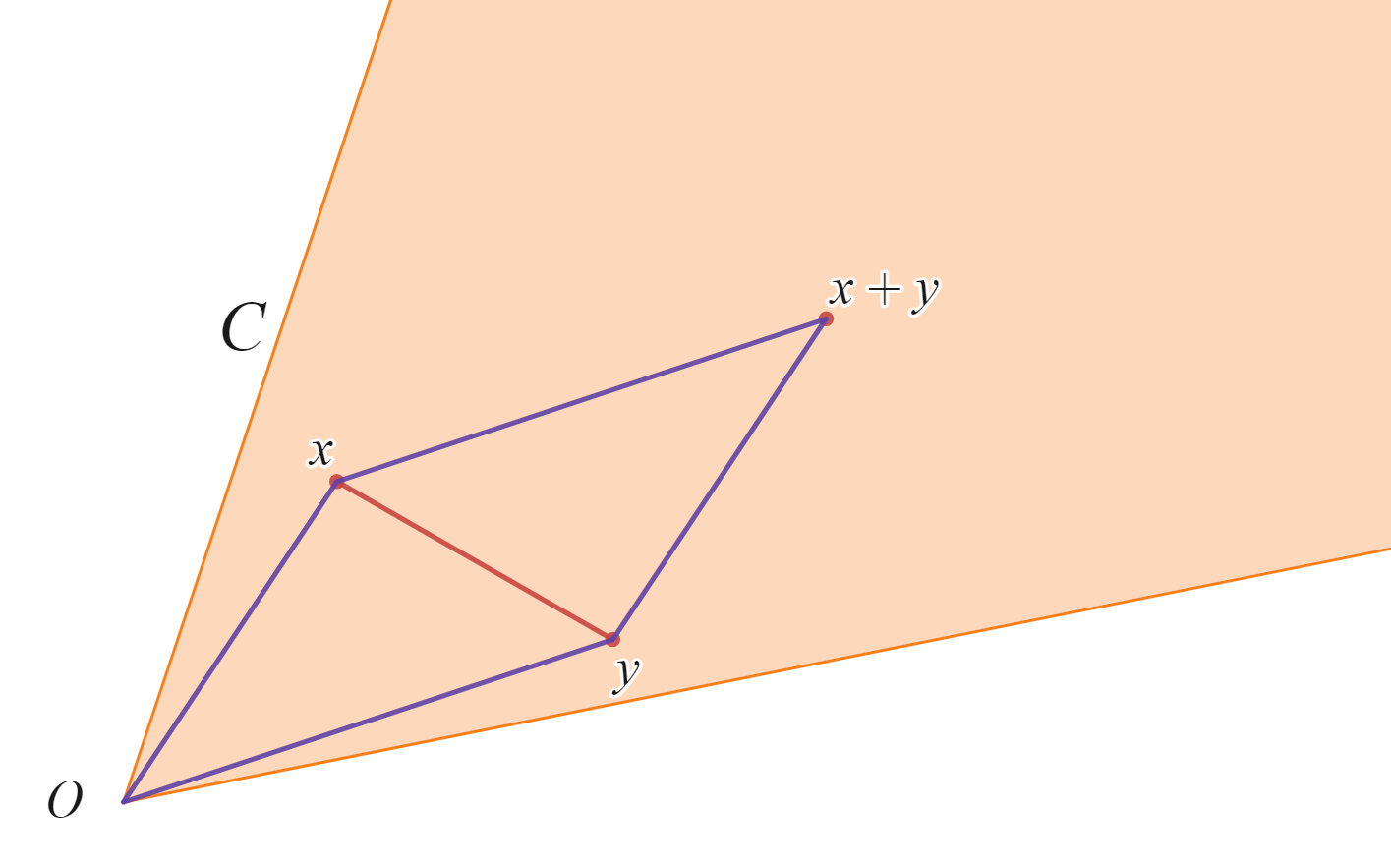convex cone（凸錐）

一方で上の図では集合$C$:coneはconvexでもあります。そしてどのように$x,y$をとっても$x+y$は$C$に含まれます。

$$A + B = \{a + b | a \in A, b \in B\}$$
$$tA = \{ta | a \in A, t \in \mathbb{R} \}$$

$$C_1,C_2:convex$$
$$\Rightarrow C_1 + C_2 :convex$$
$$C:convex$$
$$\Rightarrow tC :convex \ (t \in \mathbb{R})$$

＜証明の考え方＞
どちらについても、convex（凸）の定義をみたすことを確認すればOKなので、集合から任意の2点$x,y$を選び、$\convex{x}{y}$がその集合に含まれることを示すことを目指します。

(i) を示す。
$$\forall x,y \in C_1 + C_2 を考える。$$
$$すると、\exists x_1,y_1 \in C_1,\exists x_2,y_2 \in C_2 \ s.t. \ x = x_1 + x_2, y = y_1 + y_2 である。$$
$$C_1,C_2:convex より、 \lambdarange に対して$$
$$\convex{x_1}{y_1} \in C_1,\convex{x_2}{y_2} \in C_2 である。$$
$$このことより、\convex{x_1}{y_1} + \convex{x_2}{y_2} \in C_1 + C_2 となる。$$
$$ここで要素の式を変形していくと、$$
$$\convex{x_1}{y_1} + \convex{x_2}{y_2}$$
$$=\convex{(x_1 + x_2)}{(y_1 + y_2)}$$
$$=\convex{x}{y} \in C_1 + C_2$$
$$よって、C_1 + C_2 :convexを示すことができた。$$

(ii) を示す。
$$\forall x,y \in tC を考える。$$
$$すると、\exists \bar{x}, \bar{y} \in C \ s.t. \ x = t \bar{x} ,y = t \bar{y} \ である。$$
$$C:convexより、\lambdarange に対して、 \convex{\bar{x}}{\bar{y}} \in C である。$$
$$このことより、t (\convex{\bar{x}}{\bar{y}}) \in tC となる。$$
$$ここで要素の式を変形していくと、$$
$$t (\convex{\bar{x}}{\bar{y}})$$
$$= \convex{t \bar{x}}{t \bar{y}}$$
$$= \convex{x}{y} \in tC$$
$$よって、tC:convexを示すことができた。$$

この問題を図で確認してみます。
凸集合!FORMULA[80][19380201][0] 凸集合$C_1,C_2$
!FORMULA[81][-1360322318][0] $C_1 + C_2$

上の図のような凸集合$C_1,C_2$を考えると、$C_1 + C_2$は緑色の集合となります。そして$C_1 + C_2$もまた凸集合となっていることが分かります。

!FORMULA[85][-242467343][0] $スカラー倍tC$

この問題から見えることは集合の凸性については、和とスカラー倍をしても維持されるということです。

$$C_\alpha:任意の凸集合族$$
$$\Rightarrow \bigcap_{\alpha} :convex$$

$$\forall x,y \in \bigcap_{\alpha} C_\alphaを考えると、\forall \alpha に対して x,y \in C_\alpha である。$$
$$C_\alpha :convex より、\lambdarange に対して、\convex{x}{y} \in C_\alphaとなる。$$
$$\forall \alpha に対して\convex{x}{y} \in C_\alpha となるので、 \convex{x}{y} \in \bigcap_{\alpha} C_\alpha 、$$
$$すなわち\bigcap_{\alpha} C_\alpha :convexを示すことができた。$$