UOV : Unbalanced Oil and Vinegar

103

はじめまして, 布衣と申します. 博士後期課程の学生で, 専攻は数学, 専門は暗号です. 私の研究テーマであるUOVについて説明します. 学部1, 2年程度の知識で読めると思います.

暗号

暗号という分野があります. 素因数分解の困難性が暗号に利用されているというのは聞いたことがあると思います. 暗号と聞くと, あるメッセージを特定の人物のみが読める状態にすることを想像すると思います. しかし実際は, この技術は暗号(cryptography)という広い概念の一つに過ぎません. かつてはこの暗号化(encryption)という目的のみに焦点が当てられていた暗号技術は, 現在では多種多様な課題を解決するための強力な技術群となっています. それらのうち, 私の研究テーマであるUOVは「署名」という方式に分類されます.

署名

暗号化の敵が盗聴ならば, 署名の敵は何でしょうか. それは偽造です. 逆に言えば, 偽造できない文字列こそ署名であると言えます. 暗号技術のうち署名方式では偽造不可能性を提供します.

偽造できない文字列を実装すると何が嬉しいかというと, オンラインで契約書にサインしたり, 電子決済の際の本人確認が出来たりします. さらに現実のサインと異なり, 一度サインした文書を後から改竄できなくしたりできます.

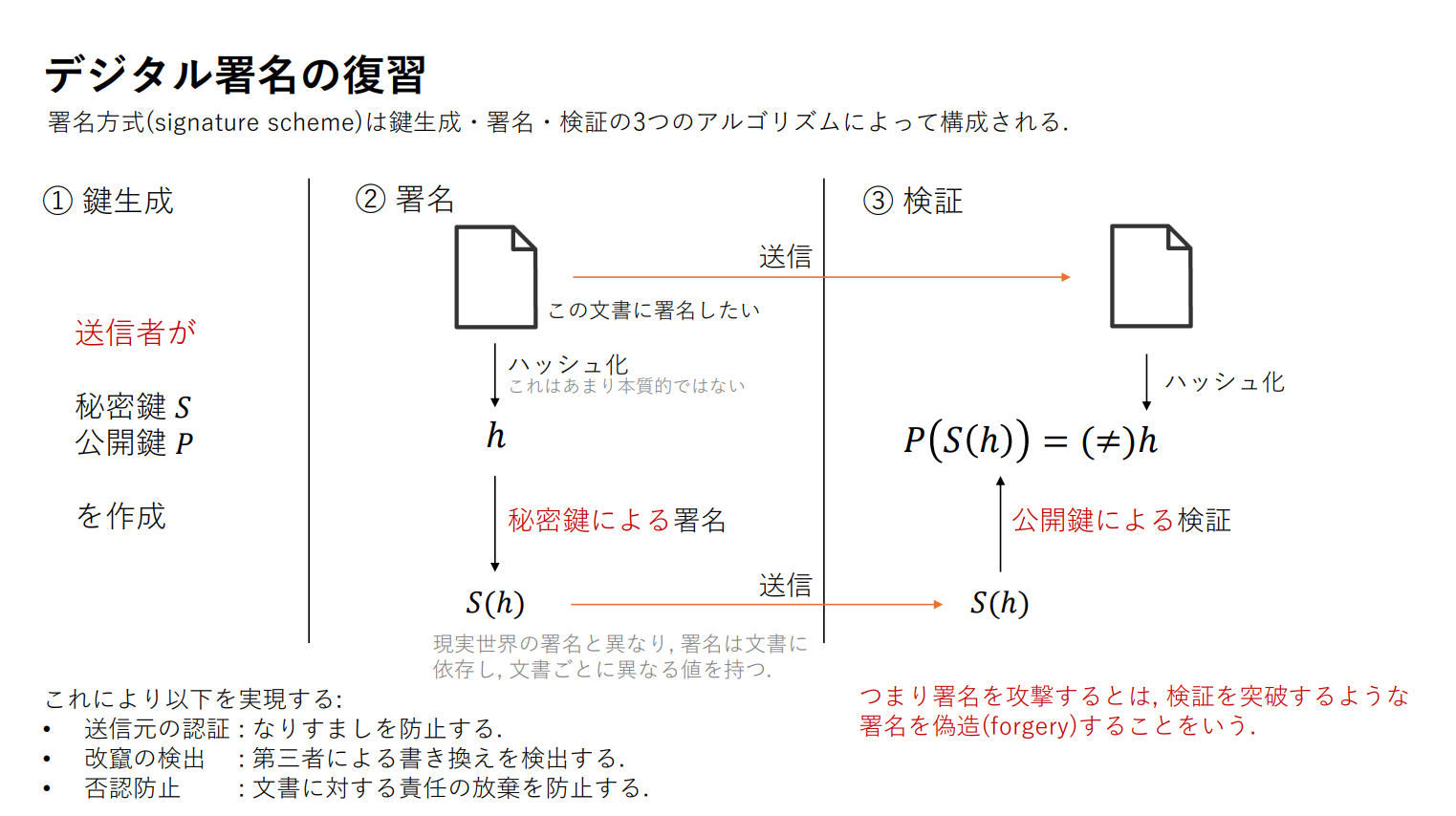署名の概要

署名方式は以下の手順で実現されます.

署名したい人が公開鍵と秘密鍵を生成する.
秘密鍵を使って文書に署名する.
署名の正当性を検証したい人は公開鍵を使って検証する.

耐量子計算機暗号

少し話が変わりますが, 量子計算機というものが台頭しつつあります. 「Shorのアルゴリズムというものがあり, 量子計算機は現在広く使われているRSA暗号や楕円曲線暗号を解読できる」というのは聞いたことがある人も多いと思います. この「暗号を解読する」というのは暗号化に限らず, 署名も, ハッシュ関数も, 乱数も, ゼロ知識証明も, マルチパーティ計算も, すべてを解読できることを意味します. 要するに安全性の根拠になっている問題を解くことができるので, その応用先は関係ないというわけです.

そのため量子計算機を用いた攻撃にも耐えうる新たな暗号, 耐量子計算機暗号を(各種の方式で)作る必要があります. 暗号の分野ではずっと前からこの耐量子計算機暗号の構築が目下の課題となっています. 新たな計算技術の脅威性はエニグマが身をもって教えてくれた教訓と言えるかもしれません.

量子計算機への対策は耐量子計算機暗号だけではありません. 他の対策としては量子暗号というものがあります. これは通信が量子化されている前提の方式で, 理論的に解読不可能と言われています. 耐量子計算機暗号の優れている点は, 古典通信, 古典計算機で動作するにもかかわらず, 量子計算機を用いても解読できないという点にあります. 今持ってるパソコンで量子計算機の脅威に対応できるのが耐量子計算機暗号です.

暗号というのはみんなが好き勝手な方式を使うと不便な上, その安全性が素人には判断できず, さらにはシステムの中に脆弱な暗号が紛れていると, そこを起点に芋づる式に攻撃されてしまう可能性があるという性質上, 普及の前に標準化という作業が行われます. 標準化では安全性だけでなく時間的, 空間的な効率も評価され, 総合的に優れた暗号が選出されます.

耐量子計算機暗号の標準化プロジェクトで代表的なのはNISTでの標準化です. これはコンペ形式で, ラウンドという区切りごとに少しずつ落選していきます. 標準化作業は現在も続いていて, UOVは現在生き残っている署名方式の一つです. UOVは20年以上様々な攻撃に耐えてきた実績と, 時間的な効率の良さが評価されています. 一方で公開鍵のデータサイズが大きい点が課題となっています.

多変数公開鍵暗号

RSA暗号の安全性の根拠は素因数分解問題です. ではUOVの根拠は何でしょうか. UOVは多変数公開鍵暗号に分類され, その安全性の根拠は(有限体上の多変数多項式からなる)連立方程式です.

線形な連立方程式は掃き出し法で解くことができます. では非線形な連立方程式はどうでしょうか. 実は解く方法がないわけではないのですが, その方法自体が計算量的に遅く, 非線形な連立方程式を解くのは困難であると言われています.

この非線形な連立方程式の求解困難性を安全性の根拠にした暗号を多変数公開鍵暗号といいます. UOVは最も基本的で最も洗練された多変数公開鍵暗号といえます. ちなみに多変数公開鍵暗号の具体的なアルゴリズムを最初に提案したのは日本人で, 松本-今井暗号と呼ばれています.

非線形であれば十分なので, よく二次多変数多項式からなる連立方程式が用いられます. この二次多項式多項式からなる連立方程式の求解問題はMQ問題といいます. UOVもMQ問題の困難性が根拠となっています.

UOV : Unbalanced Oil and Vinegar

さて, UOVの構成について説明します. UOVは前身となるOil and Vinegarが提案されてから20年以上, 安全性や効率について無数の議論を経て洗練に洗練を重ねた傑作です. ここではオリジナルとも最新版とも異なる, 最も説明しやすいバージョンで説明します.

記号

UOVは多変数公開鍵暗号に属するため, 連立方程式が登場します.
$q$ を位数とする有限体 $F_{q}$ 上で考えます. UOVの現在のパラメータでは $q$ は $16$ か $256$ です. 偶数という点に注意してください.
$n$ を変数の個数, $m$ を多項式の個数とします.
変数 $x = (x_{1}, \dots, x_{n})^{⊤}$ を分割し, 前半 $v$ 個をvinegar変数, 後半 $o$ 個をoil変数と呼びます. すなわち $v + o = n$ です.
$v$ は大きく, $o$ は小さい値を想定しておくとよいです. (これがUnbalancedの由来です)

UOVは署名方式なので, 署名したいメッセージ $μ$ と署名 $σ$ を定義します. これらは $F_{q}$ の元の列で表現され, $μ \in F_{q}^{m}$ , $σ \in F_{q}^{n}$ です.

鍵生成

鍵生成では署名したい人が秘密鍵と公開鍵を生成します.

まず, oil変数のみからなる項を含まない二次形式を $m$ 個ランダムに生成します. これを $F (x) = (f_{1} (x), \dots, f_{m} (x))$ とします. すなわち, 各 $k = 1, \dots, m$ について,

$\begin{array}{r} f_{k} = \sum_{\begin{array}{c} i = 1, \dots, n \\ j = 1, \dots, v \end{array}} c_{i j}^{k} x_{i} x_{j} \end{array}$

と書くことができます. なんか数式が中央に来ないな.

この二次形式列は「oil変数のみからなる項を含まない」という性質があります. この性質により, 連立方程式としては全く難しくありません(署名のところで説明します). これを「難しい連立方程式」に変換します.

正則な $n$ 次正方行列 $S$ をランダムに生成し, 合成写像
$\begin{array}{r} P (x) = F \circ S (x) \end{array}$
で二次形式列 $P$ を構成します. これは $F$ に変数変換 $x \mapsto S x$ を適用しています. これにより「oil変数のみからなる項を含まない二次形式列」 $F$ を「一見ランダムな二次形式列」 $P$ に変換します.

もとの変数列 $x$ は前半にvinegar変数, 後半にoil変数と二種類の変数が「分離して」並べられています. 一方新しい変数列 $S x$ はそれらの変数が前半にも後半にも「攪拌されて」存在します. この様子を二層に分離したドレッシングを混ぜる様子に見立てて Oil and Vinegar と名付けられました.

$P = F \circ S$ のうち, $P$ を公開鍵, $S$ を秘密鍵とします. $F$ も秘密にする必要がありますが, $S$ と $P$ から $F = P \circ S^{- 1}$ を計算できるので, $F$ を秘密鍵と呼ぶかどうかはどちらでも構いません.

$P$ は一見ランダムな二次形式列と書きました. 実際 $P$ は共通の $o$ 次完全等方部分空間を持つという特殊な性質があり, 完全にランダムな二次形式列ではありません. しかし, $P$ のこの性質を利用する効率的な攻撃は提案されていません. 言い換えると, 現状人類には $P$ と完全にランダムな二次形式列との見分けがつかないと言えます. ゆえに $P$ は「難しい連立方程式」を定義します.

署名

署名ではメッセージ $μ$ と秘密の情報 $F, S$ を使って署名 $σ$ を生成します.

目標としては $P (σ) = μ$ となるような $σ$ を計算します. しかし, $P$ は「難しい連立方程式」を定義するので, 連立方程式 $P (x) = μ$ を直接解くことはできません. そこで署名者のみが知っているヒント $F, S$ を使います.

$F (x^{'}) = μ$ を解いて, (その解 $x^{'}$ は実は変換後の $S x$ だったと思って) $x = S^{- 1} x^{'}$ を計算すれば $P (x) = μ$ を解くことができます.
( $P (x) = F \circ S \circ S^{- 1} (x^{'}) = F (x^{'}) = μ$ )

では $F (x^{'}) = μ$ はどのように解けばいいでしょうか. $F$ はoil変数のみからなる二次の項を持たないので, vinegar変数に値を代入すると式全体はoil変数のみからなる一次式になります. そこで, oil変数の個数が式の個数と同じか多い場合は, vinegar変数に適当に値を代入し, 残った線形方程式を解いてoil変数を求めれば $x^{'}$ 全体が求まります. UOVでは $m = o$ となっています. この残った線形方程式は必ず解が存在するわけではありませんが, 十分高い確率で解が存在することが知られています. もし解が無かったらvinegar変数に代入する値を変更してもう一度挑戦すればいいです.

このようにして $P (σ) = μ$ を満たす $P, σ, μ$ を送信します. $P, μ$ を固定したとき, $P (σ) = μ$ となる $σ$ は誰にでも計算できるわけではなく, $P$ に付随する秘密情報 $F, S$ を知らないと計算できません. このような秘密鍵というヒントがあると解けるけど, ヒントがないと解けないという構造をトラップドアといいます.

検証

$P (σ) = μ$ が成立することをもって署名が正当であることを確認します.

署名を偽造しようとする攻撃者は, なりすましたい相手の公開鍵 $P$ と, 偽造署名を施したい文書 $μ$ を持ってきて, (秘密鍵を使わずに) $P (σ) = μ$ を満たす $σ$ を計算する必要があります. そのためには有限体上の二次形式からなる連立方程式を解く必要があり, この問題の困難性がUOVの安全性の根拠になっています.

Toy Example

暗号は計算機が相手ですので, 非常に大きいパラメータで実装されます. しかし大きい数字で説明されてもわからないので, 小さいパラメータで具体例を構成して説明します. これを toy example といいます.

有限体だと計算しにくいので, ここでは $Q$ 上で説明します. ニュートン法のような近似的な手法などを封じるために, UOVの安全性において有限体は重要な役割を果たすのですが, 鍵生成, 署名, 検証の一連の操作において有限体の性質を使うことはありません. (そういう意味では, UOVはある種普遍的なアイデアといえるかもしれません.)

記号

変数の数 $n = 4$ として, 変数をそれぞれ $x, y, z, w$ とします. $v = o = 2$ として, $x, y$ をvinegar変数, $z, w$ をoil変数とします.
(実際は $v = o$ は脆弱なパラメータであり採用されません.)
UOVでは $o = m$ なので, 式の数 $m = 2$ ということになります.

今, $μ = (- 19, 2)$ と表現されたメッセージに署名したいとします.

鍵生成

まず, oil変数のみからなる項を含まない二次形式を $m = 2$ 個作ります.

変数 $x, y, z, w$ で構成される二次の単項式は以下の $10$ 個です.
$\begin{array}{r} x^{2}, x y, x z, x w, y^{2}, y z, y w, z^{2}, z w, w^{2} . \end{array}$
このうちoil変数 $z, w$ のみからなる単項式は,
$\begin{array}{r} z^{2}, z w, w^{2} \end{array}$
の $3$ 個です. これらを除いた
$\begin{array}{r} x^{2}, x y, x z, x w, y^{2}, y z, y w \end{array}$
に適当に係数を振り分けます.

$f_{1} (x, y, z, w) = x^{2} + 4 x y + 6 x z + 8 x w + 5 y^{2} + 12 y z + 14 y w$
$f_{2} (x, y, z, w) = 8 x^{2} + 18 x y + 20 x z + 22 x w + 12 y^{2} + 26 y z + 28 y w$

これらをまとめて $F (x, y, z, w) = (f_{1} (x, y, z, w), f_{2} (x, y, z, w))$ とおきます. これは $Q^{4}$ から $Q^{2}$ への写像という捉え方もできます.

ところで, 二次形式は対称行列としての表現を持ちます. 上の $f_{1}, f_{2}$ の場合, それぞれの表現行列は
$\begin{array}{r} [f_{1}] = (\begin{array}{cccc} 1 & 2 & 3 & 4 \\ 2 & 5 & 6 & 7 \\ 3 & 6 & 0 & 0 \\ 4 & 7 & 0 & 0 \end{array}), [f_{1}] = (\begin{array}{cccc} 8 & 9 & 10 & 11 \\ 9 & 12 & 13 & 14 \\ 10 & 13 & 0 & 0 \\ 11 & 14 & 0 & 0 \end{array}) \end{array}$
となります. ここで二次形式 $f$ の表現行列を $[f]$ で表しています.
( $f (x, y, z, w) = (x, y, z, w)^{⊤} \cdot [f] \cdot (x, y, z, w)$ )

(この表現は今 $Q$ 上で行っているから可能である点に注意してください. 標数が $2$ の体では, この方法で二次形式を対称行列で表現することはできません.)

$f_{1}, f_{2}$ の定義より, 右下の $o \times o$ 成分がすべて $0$ になっていることがわかります.

次に正則な $4$ 次正方行列 $S$ を適当に選択します. ここでは
$\begin{array}{r} S = (\begin{array}{cccc} 1 & 1 & 2 & 3 \\ 0 & 1 & 1 & 1 \\ 1 & 1 & 3 & 4 \\ 1 & 0 & 2 & 4 \end{array}) \end{array}$

とします. これが秘密鍵になります.

$S$ を使って $F$ を変数変換し, $P = (p_{1}, p_{2}) = F (S \cdot (x, y, z, w)^{⊤})$ を求めます.

$f (S \cdot (x, y, z, w)^{⊤}) = (x, y, z, w) S^{⊤} [f] S (x, y, z, w)^{⊤}$

であるから, 真ん中の $S^{⊤} [f] S$ を先に計算すれば, 変換後の二次形式が対称行列として表されます.

$\begin{array}{r} S^{⊤} [f_{1}] S = (\begin{array}{cccc} 1 & 0 & 1 & 1 \\ 1 & 1 & 1 & 0 \\ 2 & 1 & 3 & 2 \\ 3 & 1 & 4 & 4 \end{array}) \cdot (\begin{array}{cccc} 1 & 2 & 3 & 4 \\ 2 & 5 & 6 & 7 \\ 3 & 6 & 0 & 0 \\ 4 & 7 & 0 & 0 \end{array}) \cdot (\begin{array}{cccc} 1 & 1 & 2 & 3 \\ 0 & 1 & 1 & 1 \\ 1 & 1 & 3 & 4 \\ 1 & 0 & 2 & 4 \end{array}) \end{array}$

を計算すると,

$\begin{array}{r} [p_{1}] = (\begin{array}{cccc} 15 & 26 & 48 & 67 \\ 26 & 28 & 74 & 111 \\ 48 & 74 & 149 & 212 \\ 67 & 111 & 212 & 298 \end{array}) \end{array}$

が得られます. 同様に

$\begin{array}{r} S^{⊤} [f_{2}] S = (\begin{array}{cccc} 1 & 0 & 1 & 1 \\ 1 & 1 & 1 & 0 \\ 2 & 1 & 3 & 2 \\ 3 & 1 & 4 & 4 \end{array}) \cdot (\begin{array}{cccc} 8 & 9 & 10 & 11 \\ 9 & 12 & 13 & 14 \\ 10 & 13 & 0 & 0 \\ 11 & 14 & 0 & 0 \end{array}) \cdot (\begin{array}{cccc} 1 & 1 & 2 & 3 \\ 0 & 1 & 1 & 1 \\ 1 & 1 & 3 & 4 \\ 1 & 0 & 2 & 4 \end{array}) \end{array}$

を計算すると,

$\begin{array}{r} [p_{2}] = (\begin{array}{cccc} 50 & 75 & 146 & 207 \\ 75 & 84 & 207 & 307 \\ 146 & 207 & 422 & 604 \\ 207 & 307 & 604 & 858 \end{array}) \end{array}$

が得られます. すなわち公開鍵 $P (x, y, z, w) = (p_{1} (x, y, z, w), p_{2} (x, y, z, w))$ は

$p_{1} (x, y, z, w) = 15 x^{2} + 52 x y + 96 x z + 134 x w + 28 y^{2} + 148 y z + 222 y w + 149 z^{2} + 424 z w + 248 w^{2}$
$p_{2} (x, y, z, w) = 50 x^{2} + 150 x y + 292 x z + 414 x w + 84 y^{2} + 414 y z + 614 y w + 422 z^{2} + 1208 z w + 858 w^{2}$

となります. (計算が合っていれば)

署名

署名したいメッセージを $μ = (- 19, 2)$ とし, $P (x, y, z, w) = μ$ という方程式を秘密鍵を用いて解きます.

まず, $F (x) = (- 19, 2)$ を解きます. すなわち, 連立方程式

$x^{2} + 4 x y + 6 x z + 8 x w + 5 y^{2} + 12 y z + 14 y w = - 19$
$8 x^{2} + 18 x y + 20 x z + 22 x w + 12 y^{2} + 26 y z + 28 y w = 2$

を解きます. そこで, vinegar変数 $x, y$ に適当な定数 $(1, 2)$ を代入します.

$1 + 8 + 6 z + 8 w + 20 + 24 z + 28 w = - 19$
$8 + 36 + 20 z + 22 w + 48 + 52 z + 56 w = 2$

式を整理すると,

$30 z + 36 w = - 48$
$72 z + 78 w = - 90$

となり, oil変数 $z, w$ に関する線形な連立方程式を得ます. これを解いて, $(z, w) = (2, - 3)$ を得ます. ゆえに $F (x, y, z, w) = μ$ の解は $(1, 2, 2, - 3)$ です.

$\begin{array}{r} S^{- 1} = (\begin{array}{cccc} 2 & - 2 & 0 & - 1 \\ 1 & 1 & - 1 & 0 \\ - 1 & - 1 & 2 & - 1 \\ 0 & 1 & - 1 & 1 \end{array}) \end{array}$

であるから, $S^{- 1} \cdot (1, 2, 2, - 3)^{⊤} = (1, 1, 4, - 3)^{⊤}$ が署名となります.

検証

公開鍵
$p_{1} (x, y, z, w) = 15 x^{2} + 52 x y + 96 x z + 134 x w + 28 y^{2} + 148 y z + 222 y w + 149 z^{2} + 424 z w + 248 w^{2}$
$p_{2} (x, y, z, w) = 50 x^{2} + 150 x y + 292 x z + 414 x w + 84 y^{2} + 414 y z + 614 y w + 422 z^{2} + 1208 z w + 858 w^{2}$

と, メッセージ $μ = (- 19, 2)$ , および署名 $(1, 1, 4, - 3)$ が届きました. この署名が正当なものかどうかを確かめます.

公開鍵に署名を代入し, メッセージに一致するかどうかを調べます.
$p_{1} (1, 1, 4, - 3) = - 19$
$p_{2} (1, 1, 4, - 3) = 2$
となり, この署名は正当なものであることがわかりました.

署名の運用

これが私の公開鍵です. これを使って署名を検証してください. と, ネット越しで言われても信用できません. そのため, 現実世界で公開鍵を事前に登録しておく必要があります.

マイナンバーカードを作成したときのことを思い出してください. 作成したことがない人は......想像力でカバーしてください. マイナンバーカードを作るとは, 上で言う鍵生成を行うことをいいます. 役所に行って本人確認をしたはずです. あれは電子的な公開鍵と現実の特定の個人を関連付けるために必要な作業だったのです. その後パスワードのようなものを設定したはずです. 具体的な実装は知りませんが, 秘密鍵を生成するための乱数シードにでも使っていると思います. このようにして秘密鍵と公開鍵を作り, 公開鍵は役所に知らせます.

次に役所は(外注してるかもしれませんが)自身で生成した鍵を使って公開鍵に署名します. この署名を電子証明書といい, 本人確認済みの公開鍵なので信用しろという意味が込められています.

今回はマイナンバーカードを例に説明しましたが, 署名はどの社会実装においてもこのように運用されています. この本人確認や電子証明書の発行, さらには古くなって廃棄した電子証明書の管理などを行う機関を「認証局」といいます. つまり認証局とは機能の集合で, その要素として本人確認を行う「登録局」, 電子証明書の発行と失効を行う「発行局」, 問い合わせのあった電子証明書が現在有効なのか失効済みなのかの情報を提供する「リポジトリ」によって構成されています.

どの程度の信頼性を要求するかにもよりますが, この電子証明書にも本物かどうか疑う余地があります. そのため電子証明書を生成したときの公開鍵にまた別の機関が署名することがあります. このように, 署名の運用はマシン上で完結せず社会システムとしての構造があります. この社会システムを特に公開鍵基盤といいます.

ちなみに今説明している技術は紙とペン(もしくは印鑑)で行う署名と区別して電子署名などと呼ばれますが, この電子署名は電子署名法により自署や印鑑と同等の法的効力が認められています.

ところで, 現在マイナンバーカードに実装されている署名は耐量子性を持ちません. そのため近いうちに方式が新しくなるはずです. 何になるかは知りませんが, UOVは有力な候補といえます.

多変数公開鍵暗号は量子計算機の脅威が明らかとなる前から研究されていて, 当時のモチベーションはカード類への実装でした. カードでピッと処理するには検証が高速である必要があります. UOVの検証は二次形式に値を代入するだけなので, 他の方式と比べても極めて高速です. この性質と, のちに明らかとなった耐量子性を考慮すると, マイナンバーカードにUOVが実装される可能性は低くありません.