モンティ・ホール問題と確率変数と格子点
はじめに
想定している事前知識
誤解とギャップがありませんように、はじめに事前知識についてお話します。
世間一般的にモンティ・ホール問題を考えるときは、組合せなどなどで確率を計算していくことを目標にしていて、「条件付き確率」や「ベイズの定理」あたりはよく見られると思いますが、特に「ナントカ分野の予備知識が必要!!」とはあまりならないと思います。ですので、普通、ラフにモンティ・ホール問題の話題を楽しむためには以下述べるような知識が必ずしも必要というわけでないと思いますので、ご安心ください。Webでモンティ・ホール問題を検索いただくと、何となく雰囲気を感じ取れると思います。
しかし、この記事では「モンティ・ホール問題から構造を考えてみよう!」という少々マニアックな方向で話をしていきますので、主に以下のような大学数学科3年次あたりで解析学好きな方が遭遇するような事前知識を想定しています。
- 測度論と確率論の入り口部分の知識:
- 測度空間と確率空間の定義。特に有限集合での測度空間を考えます。
- 可測関数と確率変数の定義。可測関数同士の合成関数について。
これら踏まえていただいて、お読みいただけますとギャップは少ないと思います。
この記事について
この記事は、モンティ・ホール問題の確率計算について、確率変数を与えてその分布を調べることで計算してみよう、という簡単な測度論を使用した頭の体操的な遊びを備忘録としてまとめたものです。
そのついでに、それらの確率変数を実現できるような確率空間を具体的に構築できないか考えてみました。すると、格子点上に個数測度をベースとした確率空間を設定し、その上の3つの独立な確率変数を組み合わせたり、測度自体も修正したりして調整すると上手く計算できたようなので、嬉しくなった次第です。
この手のものは、やりつくされていると思いますが、私はリサーチ能力が乏しく、記事内の主張が正しいというエビデンスは見つけられていません。ですので、気が付かずに致命的な欠陥が発生している可能性もありますし、トンデモナイ感じになってる可能性もありますが、そのあたりご了承のうえ、暇つぶし程度に眺めていただければ幸いです。誤植等もありましたら、すみません。
今回は数式でもりもり進んでいく形で書いているのですが、今後暇があって気が向けばシミュレーションをしてチェックしてみたいなあ、なんてことを考えています。
(余談)モチベーション
「確率おもしろいね」的な会話をしていると、モンティ・ホール問題の話題が襲来することが多い気がします。そんな話をしているときは大抵ちょっとした立ち話くらいのラフなノリの場だったりして、毎度「なんでだろう?」など考えたりするのもなかなか難しく思うのです。なので、時間があるときに一度もにょもにょと考えてみようという算段です。
最終的にいろいろ計算できてうれしい反面、セッティングなどなどややこしくなりまして、立ち話をどうしましょう?という課題は解決されませんでした。まあ、良しとしておきましょう。
問題の設定
もとの問題は有名なので、Webで調べると大量に歴史的な背景や諸々の計算がヒットします。そちらを調査してまとめるのも一苦労なので、ここでは書きません。気になる方はぜひ調べてみてください。
今回は単純に、今考えたい問題を定義して進めていきます。
- 前提:
- N個のドアを考える($N \geq 3$)
- そのうちどれか1個のドアが「あたり」で、開くと賞品がある
- その他のドアは「はずれ」で、開いても賞品はない
- 登場人物は二人で、一人は挑戦者、もう一人は司会進行
- N個のドアを考える($N \geq 3$)
この前提のもと、以下ステップのゲームを考える
- ステップ:
- 挑戦者がドアを1個選ぶ
- 司会進行が『挑戦者が選んだドア』と『「あたり」のドア』がどれであるか確認し、以下ルールで2個のドアを選び、それ以外のドアを開く
- 『挑戦者が選んだドア』が『「あたり」のドア』でないとき、『挑戦者が選んだドア』と『「あたり」のドア』を選ぶ
- 『挑戦者が選んだドア』が『「あたり」のドア』であるとき、『挑戦者が選んだドア』(=『「あたり」のドア』)を選び、それ以外の『「はずれ」のドア』から無作為にもう1個のドアを選ぶ
- 挑戦者には再度ドアを選ぶ権利が与えられ、司会進行が選んだ2個のドア(つまり、挑戦者が最初に選んだドアか、司会進行が残したもう1個のドア)から1個を選ぶことができる
- 最終的に挑戦者が選んだドアを開き、「あたり」であれば賞品を手に入れられる
これらの設定のもとで、以下問題を考える
- 問題
- ステップ3において、挑戦者は再度ドアを選ぶことができるが、どちらのドアが「あたり」である確率が高いか?
本来、モンティ・ホール問題ではN=3の場合を考えますが、感覚的な説明をしたいときに『1億枚のドアから選ぶとしたら?』というノリの話が持ち出されることが(私の周りだと)よくあります。なので、もののついでにドアの個数はN個にして考えます。
確率変数のセッティング
さて、上の問題を考えるための確率変数を、分布を与える形でセッティングしていきます。確率変数をセッティングするうえで、都合のいい確率空間$(\Omega, \mathcal{F},\mathbb{P})$が存在すると仮定して、都合のいい分布の条件から調子よく変数を定義していき、終盤のセクションで具体的な確率空間と確率変数の構成を探します。つまり、途中までお気持ち数学で突き進んでいきます。
よく高校数学の確率の問題などですと、N個の選択肢があって「あたり」が1個であるクジ引き問題では、「あたり」を引く確率は$\frac{1}{N}$だというように一気に計算することが多いと思いますが、クジを引く操作を分解して『N個のうち「あたり」がランダムに1個決まり、さらに挑戦者もN個の選択肢から1個選ぶ。それらが一致しているときに「あたり」を引いたと判断する。』という形に分解して考えてみます。
このとき、当然「あたり」を選ぶ確率は$\frac{1}{N}$になるのですが、それは確率変数を定義した後で、実際に計算して確かめてみます。
N個のドアを$1,2,\cdots, N$と番号付けしておくことにします。
N個のドアのうち、「あたり」のドアを確率変数$T$で表すことにして、それぞれのドアが「あたり」である確率は等しいこととする:各$k=1,2,\cdots,N$に対して
$$ \mathbb{P}(T=k)=\frac{1}{N} $$N個のドアのから、挑戦者が選んだドアを確率変数$X$で表すことにして、それぞれのドアを選ぶ確率は等しいこととする:各$l=1,2,\cdots,N$に対して
$$ \mathbb{P}(X=l)=\frac{1}{N} $$$T$と$X$の選び方は素直に$N^2$パターン存在して等確率に選ばれるものとする:各$k,l=1,2,\cdots,N$に対して同時分布が
$$ \mathbb{P}(T=k,\ X=l)=\frac{1}{N^2} $$
さて、上のように確率変数$T,X$を定義すると
\begin{eqnarray}
\mathbb{P}(T=k,\ X=l)
&\ =\ & \frac{1}{N} \cdot \frac{1}{N} \ =\ \mathbb{P}(T=k) \cdot \mathbb{P}(X=l)
\end{eqnarray}
より独立になります。また、「あたり」のドアが選ばれる確率は
\begin{eqnarray}
\mathbb{P}(T=X)
&\ =\ & \sum_{k=1}^{N} \mathbb{P}(T=k ,\ X=k) \\
&\ =\ & \sum_{k=1}^{N} \frac{1}{N^2} \\
&\ =\ & \frac{1}{N}
\end{eqnarray}
より$\frac{1}{N}$となります。
これらは、ゲーム進行の操作の感覚とは大きく乖離しないと思います。一方で挑戦者の人間らしさみたいなものは表現できません。この手のゲームで挑戦者が「あたり」がどれであるか知ってしまった場合、つまり、イカサマをした場合は必ず「あたり」を選びたくなるだろうと考えられます。これを確率測度の言葉で表すと条件付き確率を考えて
$$
\mathbb{P}(X=k \ | \ T=k)=1
$$
と書けますが、$T,X$が独立である場合
$$
\mathbb{P}(X=k \ | \ T=k)=\mathbb{P}(X=k)=\frac{1}{N}
$$
となり、「あたり」がどれであるか知ってしまっても無作為にドアを選ぶ挑戦者となります。「あたり」を知ってからドアを選択するシチュエーションを考えることはありませんし、イカサマを考慮すると以下で説明する問題が発生してゲームが崩壊するため、ゲーム会場において挑戦者が「あたり」を知ったとしても無作為にドアを選ぶ仕組みが備わっているものとして進めていきます。
では、イカサマを考慮してみます。同時分布を与えないで、各$k$について$\mathbb{P}(X=k \ | \ T=k)=1$という条件によって$T,X$の関係を与えた場合
\begin{eqnarray}
1
&\ =\ &\mathbb{P}(X=k \ | \ T=k) \\\
&\ =\ & \frac{\mathbb{P}(X=k ,\ T=k)}{\mathbb{P}(T=l)} \\
&\ =\ & N \cdot \mathbb{P}(X=k ,\ T=k)
\end{eqnarray}
より
\begin{eqnarray}
\mathbb{P}(T=X)
&\ =\ & \sum_{k=1}^{N} \mathbb{P}(X=k ,\ T=k) \\
&\ =\ & \sum_{k=1}^{N} \frac{1}{N} \\
&\ =\ & 1
\end{eqnarray}
となり、$T=X \ a.s.$だから、常に「あたり」を選ぶエスパー挑戦者ができあがるためゲームになりません。
では、モンティ・ホール問題のポイントとも言える『司会進行が選択した2個のドア』を表す確率変数をセッティングしていきます。
- 2個のドアの組み合わせを値にとる確率変数を考える。つまり
$$ \Pi:=\big\{ \{ s, t \} \ |\ s \neq t\ ( s,t = 1,2, \cdots , N) \big\} $$
として$Y: \Omega \rightarrow \Pi$なる確率変数を定義する。$\Pi$には加法族$2^{\Pi}$が備わっているとする。
司会進行の行動は$T,X$を把握した後の行動に注意する必要があるため、$Y$に事後分布を与えて定義する:各$s,t,k,l = 1,2, \cdots , N(s\neq t)$に対して
\begin{eqnarray} \mathbb{P}(Y=\{s,t \} \ |\ T=k,\ X=l )= \left\{ \begin{array}{l\l} 1 & (k \neq l, \ \{k,l\}=\{s,t\})\\ 0 & (k \neq l, \ \{k,l\}\neq \{s,t\}) \\ \frac{1}{N-1} & (k = l, \ k \in \{s,t\})\\ 0 & (k = l, \ k \notin \{s,t\}) \end{array} \\ \right. \end{eqnarray}
と定義する。上二段は「あたり」と挑戦者のドアが異なる場合で、この場合は司会進行は必ず「あたり」と挑戦者のドアを選ぶ。下二段は「あたり」と挑戦者のドアが一致する場合で、司会進行は挑戦者のドアの他に、余ったN-1個のドアから1個を無作為に選ぶ。
以上でゲームに対応する確率変数たちをセッティングできました。特に$Y$がモンティ・ホール問題において、重要な役割を果たします。
不思議なことに、これまでの定義において$T,X$の各条件は対称的でして、ゲームの役割的に「あたり」のドア・挑戦者のドアという対応を与えていますが、入れ替えてしまっても数学的に差し支えありません。面白いですね。
次の項目では、これまで定義した確率変数を使用して、問題となっていた確率を算出していきます。
問題の解決
問題となる確率を得るためには、何を計算すればよいしょうか?ゲームの流れを確率変数の言葉で書き直して、注目したいポイントを整理すると次が考えられます:
- $T$と$X$の値が決定される
- [1]で決定された$T,X$に依存して$Y$の組合せが決定される
- $Y$で選ばれた2個のドアに対して、$T$はどのように分布しているか?
- さらに[3]の前提として、$Y$の組のうち片方が$X$であることが事前にわかっている
[1]と[2]では$T$の条件で$Y$が決定されていますが、[3]では逆転して$Y$の条件下での$T$に興味を持っています。これは条件付き確率の役割を反転させているため、ベイズの定理を使うと上手く理解できそうな気がします。しかし厄介なことに、[3]の$Y$の事前情報として$X$が組み込まれています。
つまり、問題への回答を得るためには、『「Xのもと決定された$Y$」のもと決定される$T$』の事後分布を計算する必要があります。この多段階の事後分布を考えるためには、『「$X$で条件付けられる確率測度」において$Y$に条件付けられる$T$の事後分布』を計算すると上手くいきそうな感じがします。
上のような多段階の条件付き確率は以下の補題でややこしさを回避することができます。
一般に確率空間$(\Omega, \mathcal{F}, \mathbb{P})$に対して、$A,B,C \in \mathcal{F}$を$\mathbb{P}(B \cap C)>0$ととり、同じ可測空間に確率測度$\mathbb{Q}_C$を
$$
\mathbb{Q}_C(\ \cdot \ )=\mathbb{P}(\ \cdot \ |\ C\ )
$$
と定義する。このとき、以下が成立する:
$$
\mathbb{Q}_C(A\ |\ B\ )=\mathbb{P}( A\ |\ B \cap C \ )
$$
\begin{eqnarray} \mathbb{Q}_C(A\ |\ B\ ) &\ =\ & \frac{\mathbb{Q}_C(A \cap B)}{\mathbb{Q}_C(B)} \\ &\ =\ & \frac{\mathbb{P}(A \cap B | C)}{\mathbb{P}(B|C)} \\ &\ =\ & \frac{\mathbb{P}(A \cap B \cap C)}{\mathbb{P}(C)} \left( \frac{\mathbb{P}(B \cap C)}{\mathbb{P}(C)} \right)^{-1} \\ &\ =\ & \frac{\mathbb{P}(A \cap B \cap C)}{\mathbb{P}(B \cap C)} \\ &\ =\ & \mathbb{P}(A\ | \ B \cap C) \end{eqnarray}
上の補題のおかげで『「$X$で条件付けられる確率測度」において$Y$に条件付けられる$T$の事後分布』は『$X,Y$によって条件付けられる$T$の事後分布』となりまして
$$
\mathbb{P}(T=k \ | \ Y=\{s,t \}, \ X=l)
$$
を計算すればよいということになります。ようやく目標が定まりました。嬉しいですね。
さて、条件となっている$X,Y$の同時分布を計算しましょう。もちろん、確率が0である事象のもとで、上記の条件付き分布を定義することはできないので注意が必要です。
各$s,t,l = 1,2, \cdots , N(s\neq t)$に対して
\begin{eqnarray}
\mathbb{P}(Y=\{s,t \} ,\ X=l )=
\left\{
\begin{array}{l\l}
\frac{1}{N(N-1)} & (l \in \{s,t\})\\
0 & (l \notin \{s,t\})
\end{array} \\
\right.
\end{eqnarray}
\begin{eqnarray}
\mathbb{P}(Y=\{s,t \} ,\ X=l )
&\ =\ & \sum_{k=1}^{N} \mathbb{P}(Y=\{s,t \} ,\ X=l, \ T=k ) \\
&\ =\ & \sum_{k=1}^{N} \mathbb{P}(Y=\{s,t \} \ |\ X=l, \ T=k )\cdot \mathbb{P}(X=l, \ T=k) \\
&\ =\ & \frac{1}{N^2} \left\{ \mathbb{P}(Y=\{s,t \} \ |\ X=l, \ T=l ) + \sum_{k\neq l} \mathbb{P}(Y=\{s,t \} \ |\ X=l, \ T=k ) \right\} \ \ \cdots (*)\\
\end{eqnarray}
ここで$l \notin \{s,t\}$であるとき、$Y$の定義から上の確率はすべて$0$となる。
また、$l \in \{s,t\}$であるとき、$s=l$として一般性は失わず、 $Y$の定義から
\begin{eqnarray}
(*)
&\ =\ & \frac{1}{N^2} \Big\{ \mathbb{P}(Y=\{l,t \} \ |\ X=l, \ T=l ) + \mathbb{P}(Y=\{l,t \} \ |\ X=l, \ T=t ) \Big\} \\
&\ =\ & \frac{1}{N^2} \left\{\frac{1}{N-1} +1 \right\} \\
&\ =\ & \frac{1}{N^2} \cdot \frac{N}{N-1} \\
&\ =\ & \frac{1}{N(N-1)}
\end{eqnarray}
この解釈としては、単純に$X$を一つ決めるごとに、$X$以外のN-1個の候補から一つピックアップされる確率となっています。$Y$が$X$と全く独立でないこともわかりました。
これで準備ができましたので、目標の確率を計算しましょう。
各$s,t,k, l = 1,2, \cdots , N(s\neq t,\ l \in \{s,t\})$に対して
\begin{eqnarray}
\mathbb{P}(T=k \ | \ Y=\{s,t \} ,\ X=l )=
\left\{
\begin{array}{l\l}
\frac{1}{N} & (k \in \{s,t\},\ k=l) \\
1-\frac{1}{N} & (k \in \{s,t\},\ k\neq l) \\
0 & (k \notin \{s,t\})
\end{array} \\
\right.
\end{eqnarray}
特にこの分布により、挑戦者が選んだドアがそのまま「あたり」である確率よりも、司会進行が選んだもう片方のドアが「あたり」である確率の方が大きい。$N$が大きければ大きいほどこの差は顕著に表れる。
\begin{eqnarray}
\mathbb{P}(T=k \ | \ Y=\{s,t \} ,\ X=l )
&\ =\ & \frac{\mathbb{P}(T=k , \ Y=\{s,t \} ,\ X=l )}{\mathbb{P}(Y=\{s,t \} ,\ X=l )}\\
&\ =\ & \frac{\mathbb{P}(Y=\{s,t \} \ |\ T=k,\ X=l ) \cdot \mathbb{P}(T=k,\ X=l )}{\mathbb{P}(Y=\{s,t \} ,\ X=l )}\\
&\ =\ & \frac{1}{N^2} \cdot \frac{\mathbb{P}(Y=\{s,t \} \ |\ T=k,\ X=l )}{\mathbb{P}(Y=\{s,t \} ,\ X=l )} \ \ \cdots (*)\\
\end{eqnarray}
ここで$k \notin \{s,t\}$のとき、$Y$の定義より$(*)=0$となる。
さて$k \in \{s,t\}$であるとする。$k=l$であるとき、分子については$Y$の定義から、分母については上で紹介した命題から
\begin{eqnarray}
(*)
&\ =\ & \frac{1}{N^2} \cdot \frac{1}{N-1} \cdot \left(\frac{1}{N(N-1)} \right)^{-1}
&\ =\ & \frac{1}{N}
\end{eqnarray}
次に$k\neq l$であるとき、こちらも上の様に計算して
\begin{eqnarray}
(*)
&\ =\ & \frac{1}{N^2} \cdot 1 \cdot \left(\frac{1}{N(N-1)} \right)^{-1}
&\ =\ & \frac{N-1}{N}
&\ =\ & 1- \frac{1}{N}
\end{eqnarray}
(余事象の確率計算を考えてもよいでしょう)
以上で問題が解決されました。めでたしめでたし。
さて、これまで理想の確率変数を好き放題作ってきましたが、これらの具体的な実態に迫っていきたいと思います。個人的に二つ気になることがあります。
- 一つは確率変数$Y$についてです。確率分布のチカラを借りて定義してきましたが、どうも計算していると、$T,X$のみに完全に決められる部分と$Y$自身が持っている確率的な性質が混ざっている部分とで、ある程度分けられそうな気がします。
- もう一つは、すべて離散型の確率変数で、値の組合せも爆発的に多いわけではないので、うまいことすると確率空間を具体的に作って、その上の確率変数の具体的な形も与えられるのではないか。
このあたりを議題として、以降のセクションを考えてみたいと思います。
確率変数$Y$の分解
このセクションでは確率変数$Y$を$T,X$の値によって決まる部分と、$T,X$の値のみでは決定しきれない部分に分解していけるものか、考えていきたいと思います。
ゲームのステップに立ち返ると、司会進行は必ず挑戦者が選んだドアを残します。つまり、$Y$の組合せのうち、片方が$X$ですから$Y=\{X, \bar{Y} \}$と表せそうです。$Y$の定義の事後分布を満たすかどうかは、$\bar{Y}$の表示を与えた後で確認します。
次に、ゲームのステップから、「あたり」のドアと挑戦者のドアが一致しているか否かで$\bar{Y}$の値の決まり方が異なりますので場合分けが必要です。
- 「あたり」のドアと挑戦者のドアが異なるとき、すでに$Y=\{X, \bar{Y} \}$で「あたり」のドアが組の一方になるので$\bar{Y}=T$となります。
- 「あたり」のドアと挑戦者のドアが一致しているとき、「あたり」のドア(=挑戦者のドア)の他のN-1個のドアから無作為に1個選びます。これはシチュエーション$\omega \in \Omega$ごとに$\{1,2, \cdots , N\} \textbackslash \{T(\omega ) \}$から等確率で1個ドアを選ぶ確率変数で表せそうです。また、このように$T$の値を基準に$Z$を決めるとき、$T\neq X$のときは$Z$の値が何であろうと$Z$を採用しないので、どんな$X$を与えられたとしても、それを無視して$T$の情報から$Z$を選んでも問題ないでしょう。つまり確率変数$Z$を新たに
\begin{eqnarray} \mathbb{P}(Z=t \ |\ T=k,\ X=l)= \left\{ \begin{array}{ll} \frac{1}{N-1}& (t \neq k, \ \forall l) \\ 0 & (t=k, \ \forall l) \end{array} \\ \right. \end{eqnarray}
という分布で定義すると良さげな感じがします。$T$と$X$の役割を交換しても大丈夫かもしれません。ちなみに、上のように$Z$を定義すると$Z$と$X$は独立になります。少し計算してみましょう。
\begin{eqnarray} \mathbb{P}(Z=t ,\ X=l) &\ =\ & \sum_{k=1}^{N} \mathbb{P}(Z=t ,\ T=k,\ X=l) \\ &\ =\ & \sum_{k\neq t} \mathbb{P}(Z=t \ |\ T=k,\ X=l) \cdot \mathbb{P}(T=k,\ X=l) \\ &\ =\ & (N-1)\cdot \frac{1}{N-1} \cdot \frac{1}{N^2}\\ &\ =\ & \frac{1}{N} \cdot \mathbb{P}(X=l)\ \ \cdots (*) \end{eqnarray}
となりまして、さらにこの$(*)$から
\begin{eqnarray} \mathbb{P}(Z=t) &\ =\ & \sum_{p=1}^{N} \mathbb{P}(Z=t ,\ X=p)\\ &\ =\ & \sum_{p=1}^{N} \frac{1}{N} \cdot \mathbb{P}(X=p) \\ &\ =\ & \frac{1}{N}\ \ \cdots (**) \end{eqnarray}
となりますので$Z$の分布が得られました。以上から$(*),(**)$を合わせて
$$ \mathbb{P}(Z=t ,\ X=l) = \mathbb{P}(Z=t) \cdot \mathbb{P}(X=l) $$
となりますので、$Z$と$X$は独立になります。個人的には直感通りの性質を持っているなと思います。ついでに$T,X,Z$の同時分布も計算してしまいましょう。
\begin{eqnarray} \mathbb{P}(Z=t ,\ T=k,\ X=l) &\ =\ & \mathbb{P}(Z=t \ |\ T=k,\ X=l) \cdot \mathbb{P}(T=k,\ X=l) \\ &\ =\ & \frac{1}{N^2} \cdot \mathbb{P}(Z=t \ |\ T=k,\ X=l)\\ &\ =\ & \left\{ \begin{array}{ll} \frac{1}{N^2(N-1)}& (t \neq k, \ \forall l) \\ 0 & (t=k, \ \forall l) \end{array} \\ \right. \end{eqnarray}
となりまして、同時分布がしっかりと計算できます。嬉しいですね。後々この同時分布を考えて確率空間と$T,X,Z$を具体的に構成します。
さて、$Y$に話を戻します。この手の場合分けを分けずに一つの関数として表す便利アイテムとして、定義関数を使います。
一般に集合$A$の部分集合$B \subset A$をとり、関数$\chi_B : A \rightarrow \mathbb{R}$を$\forall x \in A$に対して
\begin{eqnarray}
\chi_B(x)=
\left\{
\begin{array}{l\l}
1 & (x \in B) \\
0 & (x \notin B)
\end{array} \\
\right.
\end{eqnarray}
と定義する。これを定義関数と呼ぶ。
記号の簡略化ために$\{T=X\} :=\{ \omega \in \Omega | T(\omega)=X(\omega) \},\ \{T\neq X\} :=\{ \omega \in \Omega | T(\omega) \neq X(\omega) \}$などと書くとすると、各$\omega \in \Omega$に対して
$$
\bar{Y}(\omega) = T(\omega) \cdot \chi_{\{ T \neq X\}} (\omega) + Z(\omega) \cdot \chi_{\{ T = X\}} (\omega)
$$
とすると具合が良さそうです。以上合わせて$Y$を以下で定義しても良さそうだと予想できます。
上で定義した$Z$を用いて
$$
Y':=\Big\{X, \ T \cdot \chi_{\{ T \neq X\}} + Z \cdot \chi_{\{ T = X\}} \Big\}
$$
と定義すると、上でモンティ・ホール問題解決に使用した$Y$の定義を満みたすだろう。つまり、$Y'$の事後分布が$Y$の定義の事後分布と一致するはずである。
「確率変数として一致する」までは言い切れない。なぜなら、もとの$Y$の取り方も一意的である保証はないうえ、$Z$と同分布であって、同じ$\omega \in \Omega$で$Z$と異なる値をとる別の確率変数の存在について、これまでの議論では捨てきれないからである。
ちなみに、後々のセクションで分布を実現するための確率空間を二つ構築する。定義域の異なる確率変数で分布が一致するので、やはり確率変数として一意的とは言えないでしょう。
上の予想を確かめてみましょう。ゴールを確認してみると
各$s,t,k,l = 1,2, \cdots , N(s\neq t)$に対して
\begin{eqnarray}
\mathbb{P}(Y'=\{s,t \} \ |\ T=k,\ X=l )=
\left\{
\begin{array}{l\l}
1 & (k \neq l, \ \{k,l\}=\{s,t\})\\
0 & (k \neq l, \ \{k,l\}\neq \{s,t\}) \\
\frac{1}{N-1} & (k = l, \ k \in \{s,t\})\\
0 & (k = l, \ k \notin \{s,t\})
\end{array} \\
\right.
\end{eqnarray}
をチェックすれば良さそうです。
早速確認していきましょう
\begin{eqnarray}
\mathbb{P}(Y'=\{s,t \} \ |\ T=k,\ X=l )
&\ =\ & \frac{\mathbb{P}(\{Y'=\{s,t \} \} \ \cap\ \{T=k,\ X=l \})}{\mathbb{P}(T=k,\ X=l )} \\
&\ =\ & N^2 \cdot \mathbb{P}(\{\{X, \ T \cdot \chi_{\{ T \neq X\}} + Z \cdot \chi_{\{ T = X\}} \}=\{s,t \} \} \ \cap\ \{T=k,\ X=l \}) \ \ \cdots (*)
\end{eqnarray}
ここで、$k \neq l$の場合を考えます。この時、$\omega \in \{T=k,\ X=l \}$に対して
$$
\{X(\omega), \ T(\omega) \cdot \chi_{\{ T \neq X\}}(\omega) + Z(\omega) \cdot \chi_{\{ T = X\}}(\omega) \} =\{l, k \}
$$
ですから$\{T=k,\ X=l \} \subset \{\{X, \ T \cdot \chi_{\{ T \neq X\}} + Z \cdot \chi_{\{ T = X\}} \} =\{l, k \}\}$となり、$\{k,l \} = \{s,t\}$のとき
$$
(*)=N^2 \cdot \mathbb{P}(\{T=k,\ X=l \})=N^2 \cdot \frac{1}{N^2} =1
$$
となります。さらにこれより$\{k,l \} \neq \{s,t\}$のとき$(*)=0$となります。
次に$k = l$の場合を考えます。この時、$\omega \in \{T=k,\ X=k \}$に対して
$$
\{X(\omega), \ T(\omega) \cdot \chi_{\{ T \neq X\}}(\omega) + Z(\omega) \cdot \chi_{\{ T = X\}}(\omega) \} =\{k, Z(\omega) \}
$$
ですから、$k \notin \{s,t\}$のとき$(*)$の分子は空事象の確率になるため$(*)=0$となります。また、$k \in \{s,t\}$のとき、$s=k$として一般性を失わずに議論ができまして、$k=s \neq t$に注意しますと
\begin{eqnarray}
(*)
&\ =\ & N^2 \cdot \mathbb{P}(\{\{k, Z \}=\{k,t \} \} \ \cap\ \{T=k,\ X=k \})\\
&\ =\ & N^2 \cdot \mathbb{P}(Z=t, \ T=k,\ X=k )\\
&\ =\ & N^2 \cdot \frac{1}{N^2(N-1)} \\
&\ =\ & \frac{1}{N-1}
\end{eqnarray}
となります。以上から予想通り、$Y'$と$Y$の事後分布が同分布になることが確認できました。つまり、これまで上で議論してきたモンティ・ホール問題の計算はすべて$Y$を$Y'$に置き換えても成立します。分布は偉大ですね。
上手くいって嬉しい反面、正直疲れてきたので、これまでのまとめをして、このセクションを終了したいと思います。事後分布などからいろいろ確率変数を定義してきましたが、同時分布を与えてしまえば勝ちです。ですので、以下の様に説明できるでしょう。
- $(\Omega, \mathcal{F}, \mathbb{P})$を確率空間
- $\Lambda:=\{1,2,\cdots ,N\},\ \Pi:=\big\{ \{ s, t \} \ |\ s \neq t\ ( s,t = 1,2, \cdots , N) \big\}$
- $(\Lambda, 2^{\Lambda}), (\Pi, 2^{\Pi})$を可測空間
とする。このとき、確率変数$T,X,Z:\Omega \rightarrow \Lambda$を同時分布
$$
\mathbb{P}(Z=u ,\ T=k,\ X=l)=
\left\{
\begin{array}{ll}
\frac{1}{N^2(N-1)}& (u \neq k, \ \forall l) \\
0 & (u=k, \ \forall l)
\end{array} \\
\right.
$$
を持つものと仮定して、$Y:\Omega \rightarrow \Pi$を
\begin{eqnarray}
Y
&:=&\Big\{X, \ T \cdot \chi_{\{ T \neq X\}} + Z \cdot \chi_{\{ T = X\}} \Big\}\\
&=&\Big\{X, \ T \cdot \chi_{\{(p,q)\in \Lambda^2| p \neq q\}}(T,X) + Z \cdot \chi_{\{(p,q)\in \Lambda^2| p = q\}}(T,X) \Big\}
\end{eqnarray}
とする。つまり、$(\Lambda^3,2^{\Lambda^3})$を可測空間とし、可測関数$f:\Lambda^3 \rightarrow \Pi$を
$$
f(t,x,z):=\Big\{\ x, \ \ t \cdot \chi_{\{(p,q)\in \Lambda^2| p \neq q\}}(t,x) + z \cdot \chi_{\{(p,q)\in \Lambda^2| p = q\}}(t,x) \Big\}
$$
として、$Y=f(T,X,Z)$とおく。
以上のとき、各$s,t,k, l = 1,2, \cdots , N(s\neq t,\ l \in \{s,t\})$に対して
\begin{eqnarray}
\mathbb{P}(T=k \ | \ Y=\{s,t \} ,\ X=l )=
\left\{
\begin{array}{l\l}
\frac{1}{N} & (k \in \{s,t\},\ k=l) \\
1-\frac{1}{N} & (k \in \{s,t\},\ k\neq l) \\
0 & (k \notin \{s,t\})
\end{array} \\
\right.
\end{eqnarray}
である。$T$は「あたり」のドアに、$X$は挑戦者のドアに、$Y$は司会進行のドアに、$Z$は$T,X$だけでは決まらない$Y$のドアに、それぞれ対応している。
まとめるとすっきりしていい感じですね。何も知らずにこれだけ見せられてもモンティ・ホール問題感が全くないのが逆にいいですね。次のセクションでは上のまとめを参考に、確率空間$(\Omega, \mathcal{F}, \mathbb{P})$と確率変数$T,X,Z$を具体的に構成してみましょう。さらにモンティ・ホール問題感がなくなっていく様が面白いです。
確率空間と確率変数の構築 ~メイン命題1~
さてさて、これまで確率空間や確率変数を調子よく設定してきましたが、これらを具体的に構築できないものか?と気になるところです。つまり、上のまとめの仮定を満たす$(\Omega, \mathcal{F}, \mathbb{P}),T,X,Z$を構築したいというお話です。これらが構築できますと、上で議論してきたお気持ち的な部分に裏付けを与えられるでしょう。
では早速考えていきますが、あまり複雑で抽象的なものを考えるのは難しいので、個数測度をベースとして確率空間を表していくことを目標にしてみます。
一般に有限集合$A$とその加法族$2^A$を考えたとき、次の$\mathbb{P}:\Omega \rightarrow [0,1]$で$(A, 2^A, \mathbb{P})$は確率空間となる:
$$
\mathbb{P}(B):=\frac{\# B}{\# A} \ \ \ \ (B \in 2^A)
$$
ここに$\#A, \#B$はそれぞれの集合の要素数を表す。ただし$\#\emptyset =0$である。
$\#$は「個数測度」や「数え上げ測度」と呼んだりもする。
よく見慣れた場合の数を考える確率測度ですので、命題の証明は省略します。
都合の良いことに、上のまとめにある同時分布を眺めているとそのまま数え上げからセッティングできそうな感じがします。ここに同時分布の仮定を再掲します:
$$
\mathbb{P}(\ T=k,\ X=l,\ Z=u)=
\left\{
\begin{array}{ll}
\frac{1}{N^2(N-1)}& (k \neq u, \ \forall l) \\
0 & (k=u, \ \forall l)
\end{array} \\
\right.
$$
これの場合分けの条件を考えると、$(k=u, \ \forall l)$の方は確率$0$なので、一旦は、この組を全く考えない集合をベースに確率空間を考えます。つまり、
$$
\{(k,l,u)\in \Lambda^3 \ |\ k \neq u\}
$$
を眺めれば良さそうな感じがします。確率変数の形を見ると、この集合の射影を考えれば、上の分布を再現できそうです。つまり、
$$
\Omega := \{(k,l,u)\in \Lambda^3 \ |\ k\neq u\}
$$
とそのまま全体集合として定義して、$(k,l,u)\in \Omega$に対して、各要素の射影
$$
\begin{array}{l}
T(k,l,u):=k \\
X(k,l,u):=l \\
Z(k,l,u):=u
\end{array}
$$
を考えると具合が良さそうな感じがしています。$T,X,Z:\Omega \rightarrow \Lambda$で可測空間$(\Omega,2^\Omega),(\Lambda,2^\Lambda)$を考えれば、当然これは可測関数になります。そして、$\mathbb{P}$を 「$\Omega$を全体集合としたときに個数測度から作られる確率測度」として、$(\Omega, 2^\Omega, \mathbb{P})$を確率空間とします。
さて、勢いで確率空間と確率変数を定義しましたが、これらがモンティ・ホール問題を考えていたときの$T,X,Z$の分布の与え方を満足するか確かめる必要があります。このためには、新しく定義した確率空間の計算から同時分布を確かめればよさそうです。
まずは$\# \Omega$を確認しましょう。$\Omega = \{(k,l,u)\in \Lambda^3 \ |\ k\neq u\}$ですから$(k,l,u)\in \Omega$の組合せは、$N$パターンある$k$を1個固定するごとに$u$を$N-1$パターンで選び、それに関係なく$l$が$N$パターンありますので
$$
\#\Omega = \{N\cdot (N-1) \}\cdot N = N^2(N-1)
$$
となります。調子がいいですね。つまり、確率測度$\mathbb{P}$は次のように書けます:
\begin{eqnarray}
\mathbb{P}(A)=\frac{\# A}{N^2 (N-1)} \ \ \ \ (A \in 2^\Omega)
\end{eqnarray}
これから同時分布を計算していきましょう。$\forall k,\forall l,\forall u \in \Lambda$に対して
\begin{eqnarray}
\mathbb{P}(\ T=k,\ X=l,\ Z=u)
&=&\frac{ \#\{(p,q,r)\in \Omega \ |\ T(p,q,r)=k,\ X(p,q,r)=l,\ Z(p,q,r)=u\}}{N^2 (N-1)} \\
&=&\frac{ \#\{(p,q,r)\in \Omega \ |\ p=k,\ q=l,\ r=u\}}{N^2 (N-1)} \\
\end{eqnarray}
とできますので、$k \neq u$のとき
$$
\mathbb{P}(\ T=k,\ X=l,\ Z=u)=\frac{ \#\{(k,l,u)\}}{N^2 (N-1)}=\frac{1}{N^2 (N-1)}
$$
と計算できまして、$k = u$のとき
$$
\mathbb{P}(\ T=k,\ X=l,\ Z=u)=\frac{ \#\emptyset}{N^2 (N-1)}=0
$$
となりますので、同時分布が計算できました。つまり、$(\Omega, 2^\Omega, \mathbb{P}),T,X,Z$のセッティングはこれでうまくできたみたいです。以上をまとめますと、前セクションのモンティ・ホール問題のまとめは次のように書けます。
- $\Lambda:=\{1,2,\cdots ,N\},\ \Pi:=\big\{ \{ s, t \} \ |\ s \neq t\ ( s,t = 1,2, \cdots , N) \big\}$
- $(\Lambda, 2^{\Lambda}), (\Pi, 2^{\Pi})$を可測空間
とする。また確率空間$(\Omega, 2^\Omega, \mathbb{P})$を
$$
\Omega := \{(k,l,u)\in \Lambda^3 \ |\ k\neq u\}, \ \ \ \ \mathbb{P}(A):=\frac{\# A}{\#\Omega} = \frac{\# A}{N^2 (N-1)} \ \ (A \in 2^\Omega)
$$
とする。確率変数$T,X,Z:\Omega \rightarrow \Lambda$を$(k,l,u)\in \Omega$に対して、各要素の射影
$$
T(k,l,u):=k, \ \ \ \ X(k,l,u):=l, \ \ \ \ Z(k,l,u):=u
$$
とする。このとき、同時分布は
$$
\mathbb{P}(\ T=k,\ X=l,\ Z=u)=
\left\{
\begin{array}{ll}
\frac{1}{N^2(N-1)}& (k \neq u, \ \forall l) \\
0 & (k=u, \ \forall l)
\end{array} \\
\right.
$$
となる。また、$Y:\Omega \rightarrow \Pi$を
\begin{eqnarray}
Y
&:=&\Big\{X, \ T \cdot \chi_{\{ T \neq X\}} + Z \cdot \chi_{\{ T = X\}} \Big\}\\
&=&\Big\{X, \ T \cdot \chi_{\{(p,q)\in \Lambda^2| p \neq q\}}(T,X) + Z \cdot \chi_{\{(p,q)\in \Lambda^2| p = q\}}(T,X) \Big\}
\end{eqnarray}
とする。つまり、$(\Lambda^3,2^{\Lambda^3})$を可測空間とし、可測関数$f:\Lambda^3 \rightarrow \Pi$を
$$
f(t,x,z):=\Big\{\ x, \ \ t \cdot \chi_{\{(p,q)\in \Lambda^2| p \neq q\}}(t,x) + z \cdot \chi_{\{(p,q)\in \Lambda^2| p = q\}}(t,x) \Big\}
$$
として、$Y=f(T,X,Z)$とおく。
以上のとき、各$s,t,k, l = 1,2, \cdots , N(s\neq t,\ l \in \{s,t\})$に対して
\begin{eqnarray}
\mathbb{P}(T=k \ | \ Y=\{s,t \} ,\ X=l )=
\left\{
\begin{array}{l\l}
\frac{1}{N} & (k \in \{s,t\},\ k=l) \\
1-\frac{1}{N} & (k \in \{s,t\},\ k\neq l) \\
0 & (k \notin \{s,t\})
\end{array} \\
\right.
\end{eqnarray}
である。$T$は「あたり」のドアに、$X$は挑戦者のドアに、$Y$は司会進行のドアに、$Z$は$T,X$だけでは決まらない$Y$のドアに、それぞれ対応している。
いい具合に書き下せたような感じがします。やっとフワフワ感のない形の命題に落ち着いたのかなと思います。この記事のメイン命題の一つ目までたどり着きましたので、ひと段落といった感触です。次のセクションでは、このメイン命題をもう少し改造を試みてみましょう。
確率空間の拡張改造 ~メイン命題2~
さて、上でモンティ・ホール問題の解決に必要な構造を一つ与えました。何となく気になるのが、$Z$を射影で与えているため、$\Omega$の条件を緩めて格子点に変えてあげると、$T,Z$の非独立な関係は測度側に押し付けられるのでは、と思うのです。
個数測度をもとにした確率測度の条件付き確率測度について、以下の補題を準備します。
一般に$(\Omega, 2^\Omega, \mathbb{P})$を、有限集合$\Omega$に個数測度をもとにした確率測度を与えた確率空間であるとする。
このとき、$A\in 2^\Omega$を$\mathbb{P}(A)>0$としてとり、以下二つの確率空間を考える:
- $(\Omega , 2^\Omega, \mathbb{P}(\ \cdot \ | A) )$
- $(A, 2^A, \mathbb{P}_A)$:ここに$\mathbb{P}_A$は$A$を全事象としたときの個数測度をもとにした確率測度
以上の時、$\forall B \in 2^\Omega$に対して
$$
\mathbb{P}(B|A)=\mathbb{P}_A(B\cap A)=\frac{\# (B \cap A)}{\# A}
$$
加法族がそれぞれ冪集合であるから、$B \cap A \in 2^A$に注意する。
\begin{eqnarray}
\mathbb{P}(B|A)
&=& \frac{\mathbb{P}(B\cap A)}{\mathbb{P}(A)} \\
&=& \frac{\# (B \cap A)}{\# \Omega} \left( \frac{\# A}{\# \Omega} \right)^{-1}\\
&=& \frac{\# (B \cap A)}{\# A} \\
&=& \mathbb{P}_A(B \cap A)
\end{eqnarray}
ここでメイン命題1の確率空間$(\Omega, 2^\Omega, \mathbb{P}_\Omega)$
$$
\Omega = \{(k,l,u)\in \Lambda^3 \ |\ k\neq u\}, \ \ \ \ \mathbb{P}_\Omega(A)=\frac{\# A}{\#\Omega} = \frac{\# A}{N^2 (N-1)} \ \ (A \in 2^\Omega)
$$
に対して、確率空間$(\Omega_0, 2^{\Omega_0}, \mathbb{P}_{\Omega_0})$を
$$
\Omega_0:=\Lambda^3, \ \ \ \ \mathbb{P}_{\Omega_0} (A)=\frac{\# A}{\#\Omega_0} = \frac{\# A}{N^3} \ \ (A \in 2^{\Omega_0})
$$
で定義すると、上の補題から$\forall A \in 2^{\Omega_0}$に対して
$$
\mathbb{P}_{\Omega_0}(A|\Omega)=\mathbb{P}_\Omega(A \cap \Omega)=\frac{\# (A\cap \Omega)}{\#\Omega}= \frac{\# (A\cap \Omega)}{N^2 (N-1)}
$$
となります。この$(\Omega_0, 2^{\Omega_0}, \mathbb{P}_{\Omega_0})$に$T_{\Omega_0},X_{\Omega_0},Z_{\Omega_0}:\Omega_0 \rightarrow \Lambda$を射影
$$
T_{\Omega_0}(k,l,u):=k, \ \ \ \ X_{\Omega_0}(k,l,u):=l, \ \ \ \ Z_{\Omega_0}(k,l,u):=u
$$
で定義しますと、これらは確率測度$\mathbb{P}_{\Omega_0}$のもとで独立になります。ほとんど自明ですが、一応確認しましょう。$\forall k, \forall l, \forall u \in \Lambda$に対して
\begin{eqnarray}
\mathbb{P}_{\Omega_0}(T_{\Omega_0}=k, X_{\Omega_0}=l, Z_{\Omega_0}=u)
&=&\frac{ \# \{(k,l,u) \}}{N^3} \\
&=& \frac{ 1}{N^3} \\
&=& \frac{ N^2}{N^3} \cdot \frac{ N^2}{N^3} \cdot \frac{ N^2}{N^3} \\
&=&\frac{ \# \{(p,q,r) \in \Omega_0\ |\ p=k \}}{N^3} \cdot \frac{ \# \{(p,q,r) \in \Omega_0\ |\ q=l \}}{N^3} \cdot \frac{ \# \{(p,q,r) \in \Omega_0\ |\ r=u \}}{N^3} \\
&=& \mathbb{P}_{\Omega_0}(T_{\Omega_0}=k) \cdot \mathbb{P}_{\Omega_0}(X_{\Omega_0}=l) \cdot \mathbb{P}_{\Omega_0}(Z_{\Omega_0}=u)
\end{eqnarray}
となりますので、独立となります。また、これらの$\mathbb{P}_{\Omega_0}$での事後分布が、メイン命題1の同時分布と一致するか確認しましょう。つまり
$$
\mathbb{P}_{\Omega_0}(\ T_{\Omega_0}=k,\ X_{\Omega_0}=l,\ Z_{\Omega_0}=u \ |\ \Omega)=
\left\{
\begin{array}{ll}
\frac{1}{N^2(N-1)}& (k \neq u, \ \forall l) \\
0 & (k=u, \ \forall l)
\end{array} \\
\right.
$$
をチェックしてみたいのですが、上の補題のおかげで
\begin{eqnarray}
\mathbb{P}_{\Omega_0}(\ T_{\Omega_0}=k,\ X_{\Omega_0}=l,\ Z_{\Omega_0}=u \ |\ \Omega)
&=&\mathbb{P}_{\Omega}(\{ \ T_{\Omega_0}=k,\ X_{\Omega_0}=l,\ Z_{\Omega_0}=u \} \cap \Omega) \\
&=& \frac{\# [\{(k,l,u) \}\cap \{(p,q,r)\in \Lambda^3 \ |\ p\neq r\} ]}{N^2 (N-1)}\\
&=&
\left\{
\begin{array}{ll}
\frac{\# \{(k,l,u) \}}{N^2 (N-1)}& (k \neq u, \ \forall l) \\
\frac{\# \emptyset}{N^2 (N-1)} & (k=u, \ \forall l)
\end{array} \\
\right. \\
&=&
\left\{
\begin{array}{ll}
\frac{1}{N^2(N-1)}& (k \neq u, \ \forall l) \\
0 & (k=u, \ \forall l)
\end{array} \\
\right.
\end{eqnarray}
となりまして、事後分布がメイン命題1の同時分布と一致します。また、条件付き確率測度$\mathbb{Q}_{\Omega_0}(\ \cdot \ ):=\mathbb{P}_{\Omega_0}(\ \cdot \ |\Omega) $と上の結果、さらに以前登場した補題『「多段階な条件付き確率」は「積事象による1段階の条件付き確率」』を合わせると、メイン命題1の結論は
\begin{eqnarray}
\mathbb{P}_\Omega(T_\Omega =k \ | \ Y _\Omega =\{s,t \} ,\ X_\Omega =l )
&=&\mathbb{Q}_{\Omega_0}(T_{\Omega_0} =k \ | \ Y_{\Omega_0} =\{s,t \} ,\ X_{\Omega_0} =l )\\
&=&\mathbb{P}_{\Omega_0}(T_{\Omega_0} =k \ | \{ Y_{\Omega_0} =\{s,t \} ,\ X_{\Omega_0} =l \} \cap \Omega)
\end{eqnarray}
と書けます。ここに、$T_\Omega , Y _\Omega , X_\Omega$は$\Omega$で定義され、$Y_{\Omega_0}$は$\Omega_0$で定義された、メイン命題1に対応する確率変数です。
以上から、「格子点$\Omega_0$」で個数測度をもとにした確率測度を考え、「射影からなる独立な確率変数」3つと「メイン命題1の全事象$\Omega$」を組合わせることでメイン命題1の結論を達成できることが分かりました。
【余談】
特に$N=6$のときは独立な3つのサイコロ投げを考えるときの確率空間と同じものになりますね。個人的にこういった感じで構造を抽象的にもにょもにょすると、別のゲームや現象と共通点が見出せるところに数学の一つの面白みを感じています。
いろいろ考えましたが、式としてはメイン命題1よりごちゃごちゃしていますし、確率空間も必要以上に大きくなっているので美しくないかもしれません。正直モンティ・ホール問題感はありませんので、ゲームを理解するならメイン命題1のままの方が良いかもしれませんね。
さて、上の計算をまとめると以下のようになります。
- $\Lambda:=\{1,2,\cdots ,N\},\ \Pi:=\big\{ \{ s, t \} \ |\ s \neq t\ ( s,t = 1,2, \cdots , N) \big\}$
- $(\Lambda, 2^{\Lambda}), (\Pi, 2^{\Pi})$を可測空間
- $\Omega_0 :=\Lambda^3$として、$(\Omega_0 , 2^{\Omega_0}, \mathbb{P})$を個数測度をもとにした確率空間
- $\Omega := \{ (k,l,u) \in \Omega_0 \ | \ k \neq u \} \subset \Omega_0$
- $\mathbb{Q}(\ \cdot \ ) := \mathbb{P}(\ \cdot \ |\Omega) $として、$(\Omega_0 , 2^{\Omega_0}, \mathbb{Q})$を確率空間
とする。このとき
$$
\mathbb{P}(A) = \frac{\# A}{N^3}, \ \ \ \ \mathbb{Q}(A) = \frac{\# (A \cap \Omega)}{N^2 (N-1)} \ \ (A \in 2^{\Omega_0})
$$
である。また確率変数$T,X,Z:\Omega_0 \rightarrow \Lambda$を$(k,l,u)\in \Omega_0$に対して、各要素の射影
$$
T(k,l,u):=k, \ \ \ \ X(k,l,u):=l, \ \ \ \ Z(k,l,u):=u
$$
とする。このとき、これらは$\mathbb{P}$のもとで独立で、同時分布は
\begin{eqnarray}
&\mathbb{P}(\ T=k,\ X=l,\ Z=u)&= \frac{1}{N^3} \ \ (\forall k,\ \forall l,\ \forall u)\\
&\mathbb{Q}(\ T=k,\ X=l,\ Z=u)&=
\left\{
\begin{array}{ll}
\frac{1}{N^2(N-1)}& (k \neq u, \ \forall l) \\
0 & (k=u, \ \forall l)
\end{array} \\
\right.
\end{eqnarray}
である。また、$Y:\Omega_0 \rightarrow \Pi$を
\begin{eqnarray}
Y
&:=&\Big\{X, \ T \cdot \chi_{\{ T \neq X\}} + Z \cdot \chi_{\{ T = X\}} \Big\}\\
&=&\Big\{X, \ T \cdot \chi_{\{(p,q)\in \Lambda^2| p \neq q\}}(T,X) + Z \cdot \chi_{\{(p,q)\in \Lambda^2| p = q\}}(T,X) \Big\}
\end{eqnarray}
とする。つまり、$(\Lambda^3,2^{\Lambda^3})$を可測空間とし、可測関数$f:\Lambda^3 \rightarrow \Pi$を
$$
f(t,x,z):=\Big\{\ x, \ \ t \cdot \chi_{\{(p,q)\in \Lambda^2| p \neq q\}}(t,x) + z \cdot \chi_{\{(p,q)\in \Lambda^2| p = q\}}(t,x) \Big\}
$$
として、$Y=f(T,X,Z)$とおく。
以上のとき、各$s,t,k, l = 1,2, \cdots , N(s\neq t,\ l \in \{s,t\})$に対して
\begin{eqnarray}
\mathbb{Q}(T=k \ | \ Y=\{s,t \} ,\ X=l )
&=& \mathbb{P}(T=k \ | \ \{Y=\{s,t \} ,\ X=l \} \cap \Omega)\\
&=&
\left\{
\begin{array}{l\l}
\frac{1}{N} & (k \in \{s,t\},\ k=l) \\
1-\frac{1}{N} & (k \in \{s,t\},\ k\neq l) \\
0 & (k \notin \{s,t\})
\end{array} \\
\right.
\end{eqnarray}
である。$T$は「あたり」のドアに、$X$は挑戦者のドアに、$Y$は司会進行のドアに、$Z$は$T,X$だけでは決まらない$Y$のドアに、それぞれ対応している。
ここで気を付けておきたいことは、一つの確率分布を実現するための確率空間の構成は、まったく一意でないということです。少なくとも「メイン命題1」の$(\Omega, 2^\Omega, \mathbb{P})$と「メイン命題2」の$(\Omega_0 , 2^{\Omega_0}, \mathbb{Q})$を考えると、別々の確率空間で同時分布が等しい確率変数の組が構築されていますし、これらに尽きないでしょう。
おわりに
ここまでお読みいただき、ありがとうございます。だらだらと深夜のテンションで書いていましたので、かなり読みづらかったと思います。
いろいろ考えてきましたが、大変疲れましたので、今回はこのあたりまでにしたいと思います。冒頭でもお話ししましたが、ものすごく暇で気が向いたときに、シミュレーションして確認してみたいと思います。シミュレーションしてみて全然違う確率になると、これまでの議論はほぼ水の泡です。怖いですね。
おまけ
メイン命題1の確率空間を考えると、お絵描きと数え上げで確率が計算できます。下の写真は$N=4$です。
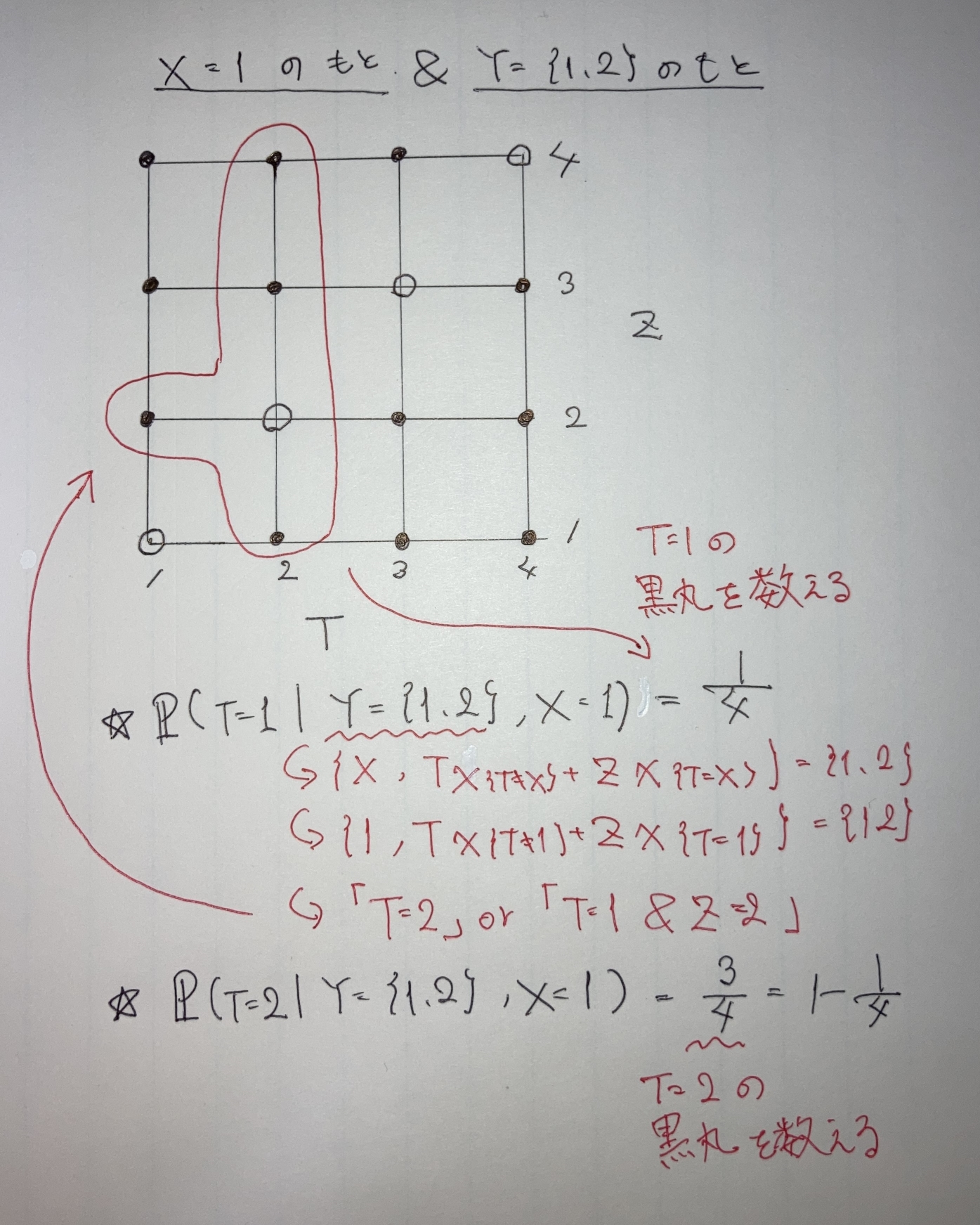 お絵描き
お絵描き
