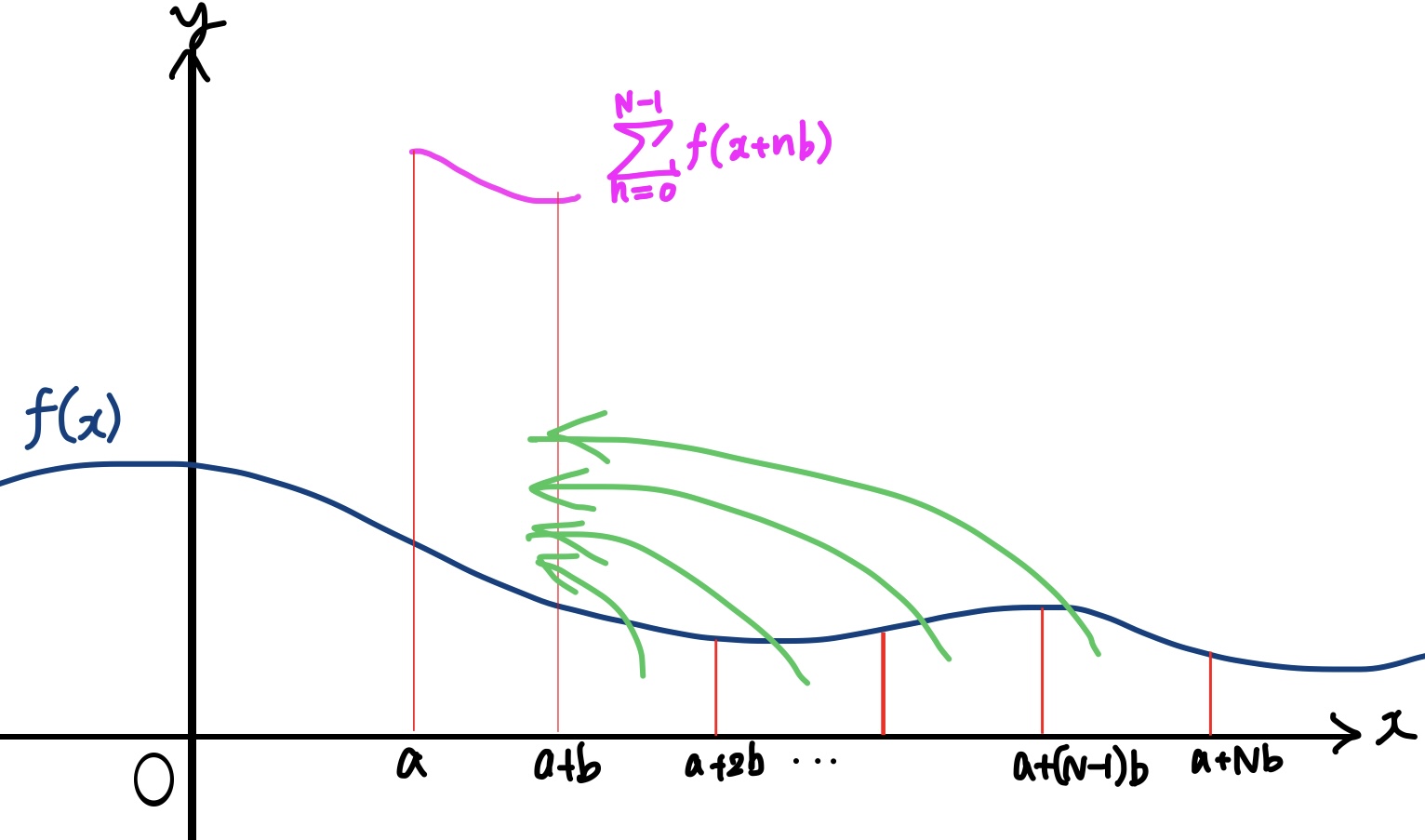
分割し重ねることで無限区間積分を有限区間積分にする
定理
$\N_0$は$0$を含む自然数。
$\displaystyle \sum_{n=N}^{N-1}x_n$は空和($0$)とみなす。
$\displaystyle \int_a^{a+Nb} f(x)dx = \int_a^{a+b} \sum_{n=0}^{N-1}f(x+nb)dx \quad(N\in\N_0) $
$\displaystyle \uhen = \sum_{n=0}^{N-1} \int_a^{a+b}f(x+nb)dx = \sum_{n=0}^{N-1} \int_{a+nb}^{a+(n+1)b}f(x)dx = \sahen $
系
超幾何関数
Wikipedia:
超幾何関数${}_rF_s$
$\beginend{align}{
&(x)_n := \prod_{k=0}^{n-1}(x+k)
\quad(\text{ポッホハマー記号}) \\
&(a_1,\range a2r)_n := \prod_{k=1}^r (a_k)_n
}$
$\displaystyle \int_0^\infty \frac{\prod_{k=1}^r\Gamma(a_k+t)} {\prod_{k=1}^s\hspace{1pt}\Gamma(b_k+t)}x^t dt = \int_0^1 \frac{\prod_{k=1}^r\Gamma(a_k+t)} {\prod_{k=1}^s\hspace{1pt}\Gamma(b_k+t)}x^t \hygeo{r+1}F{s} {\rangeex{}a{+t}1r,1} {\rangeex{}b{+t}1s}{x} dt $
$\beginend{align}{ \sahen &= \int_0^1 \sum_{n=0}^\infty \frac{\prod_{k=1}^r\Gamma(a_k+t+n)} {\prod_{k=1}^s\hspace{1pt}\Gamma(b_k+t+n)}x^{t+n} dt \\&= \int_0^1 \frac{\prod_{k=1}^r\Gamma(a_k+t)} {\prod_{k=1}^s\hspace{1pt}\Gamma(b_k+t)}x^t \sum_{n=0}^\infty \frac{(\rangeex{}a{+t}1r)_n}{(\rangeex{}b{+t}1s)_n}x^n dt \\&= \uhen }$
$\displaystyle \int_0^\infty \frac{\Gamma(a+t)}{\Gamma(b+t)} dt = \frac1{b-a-1} \int_0^1 \frac{\Gamma(a+t)}{\Gamma(b+t-1)} dt $
$\beginend{align}{ \sahen &= \int_0^1 \frac{\Gamma(a+t)}{\Gamma(b+t)}\hygeo2F1{a+t,1}{b+t}{1} dt \\&= \int_0^1 \frac{\Gamma(a+t)}{\color{red}\Gamma(b+t)} \frac{{\color{red}\Gamma(b+t)} {\color{blue}\Gamma(b-a-1)}}{{\color{blue}\Gamma(b-a)}\Gamma(b+t-1)} dt \quad\because\text{超幾何定理}\\&= \uhen }$
$\displaystyle \int_a^\infty \frac{dt}{(t)_n} = \frac1{n-1} \int_a^{a+1} \frac{dt}{(t)_{n-1}} $
$\beginend{align}{ \sahen &= \int_0^\infty \frac{dt}{(a+t)_n} = \int_0^\infty \frac{\Gamma(a+t)}{\Gamma(a+n+t)} dt \\&= \frac1{n-1} \int_0^1 \frac{\Gamma(a+t)}{\Gamma(a+n+t-1)} dt = \frac1{n-1} \int_0^1 \frac{dt}{(a+t)_{n-1}} \\&= \uhen }$
レルヒの超越関数
Wikipedia: レルヒの超越関数(英)$\Phi(x,s,a)$ 、 不完全ガンマ関数$\Gamma(s,x)$
$\displaystyle \int_a^{a+1} x^t\Phi(x,s,t) dt = (-\ln x)^{s-1}\Gamma(1-s,-a\ln x) \quad(0< x<1) $
$\beginend{align}{ \sahen &= \int_a^\infty t^{-s}x^t dt \\&= (-\ln x)^{s-1} \int_{-a\ln x}^\infty u^{-s}e^{-u} du \quad\lr({t = -\frac u{\ln x}})\\&= \uhen }$