応用数学解説

文献あり

宇宙の時間を巻き戻す方法

physlab2026アドベントカレンダー,宇宙論,一般相対性理論

238

[本記事はPhysics Lab. Advent Calender2026の10日目の記事です。]

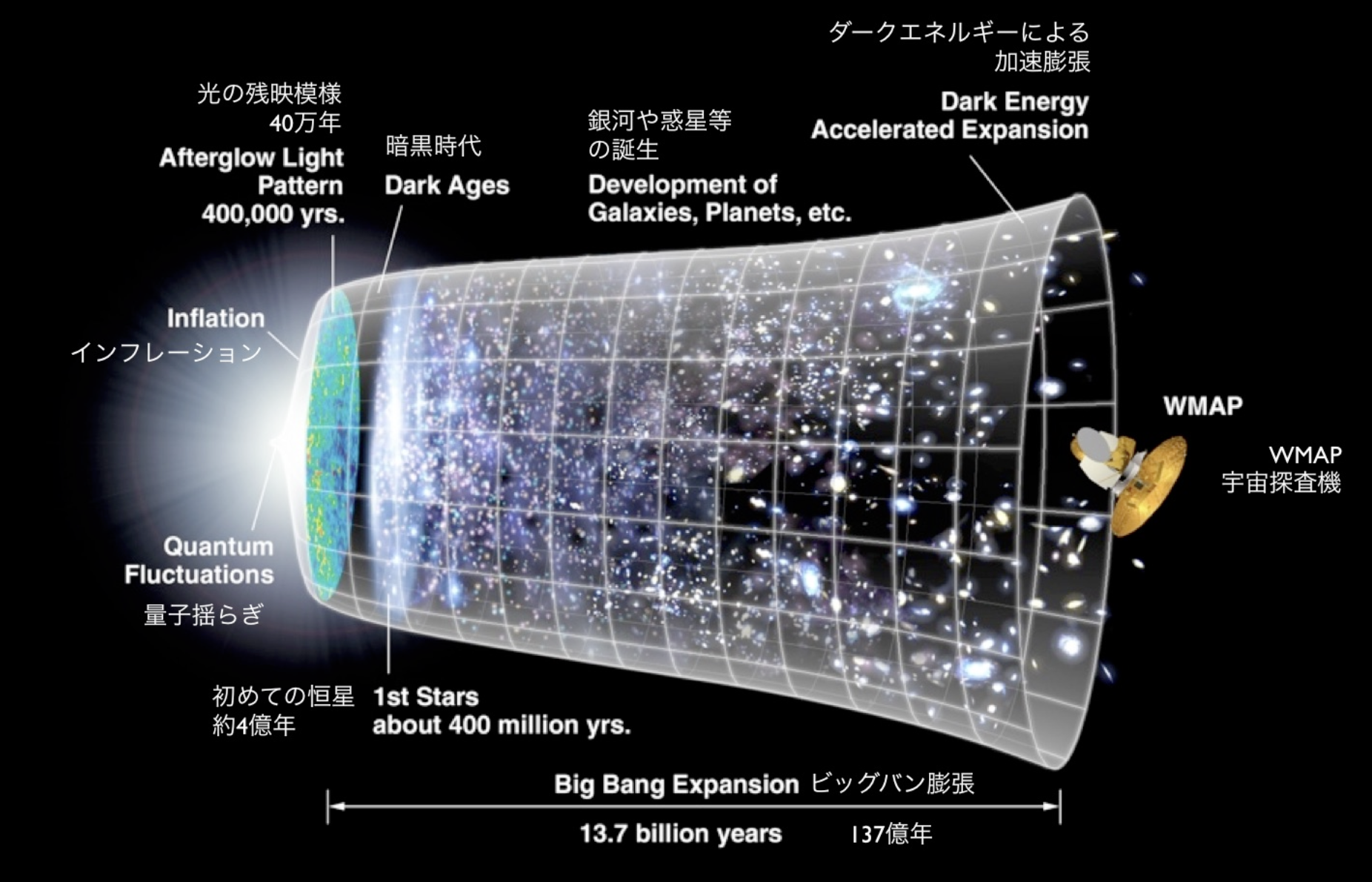宇宙膨張　NASA/WMAP Science Teamより引用

はじめに ~ 465億光年という謎

夜空を見上げるとき、私たちは「過去」を見ています。星々の光は何億年、何十億年という長い旅を経て、今この瞬間に私たちの瞳に届いているからです。

よく「宇宙の年齢は138億年」だと言われます。ならば、私たちが見ることのできる宇宙の果ては、単純に138億光年先なのでしょうか？
直感的にはそう思えるかもしれません。光が138億年かけて進んだ距離なのだから、と。

しかし、この宇宙は私たちの想像よりも遥かに奥深く、ダイナミックです。
実は、光が旅をしている間にも宇宙空間そのものが絶えず膨張し続けているため、観測可能な宇宙の「果て」は、138億光年よりもずっと遠くへと遠ざかっているのです。その距離、実に465億光年。138億年という時を超えて広がり続けたこの宇宙の真の姿を、私たちは直感だけで理解することはできません。

そこで本記事では、一般相対性理論と現代宇宙論の標準的なモデル「$\Lambda$-CDMモデル」を地図にして、この広大な時空の旅に出かけます。数式という名の望遠鏡を使って宇宙の時間を巻き戻し、その誕生と広がりの秘密に迫ってみましょう。

対象読者

特殊相対論までは勉強したことがある人
一般相対性理論を勉強してないけど聞き齧ったことがある人
数式がたくさんあると嬉しい人
何より宇宙が大好きな人

旅の準備

自然単位系

$$ \hbar = c = k_B = 1$$
それぞれディラック定数、光速、ボルツマン定数を指しています。

換算係数を1とすることで、物理の本質を見やすくしています。
この単位系ではエネルギー(=質量)の単位のみを使って物理量の単位を考えるようになり、距離(=時間)の単位はその逆数になります。

添え字と縮約

ギリシャ文字の添え字はそれぞれ次の数字を取ります。
$$\mu, \nu, \dots = 0, 1, 2, 3$$
$0$が時間成分(エネルギー成分)、$1, 2, 3$が空間成分(運動量成分)を表します。

この後出てくる添え字付きの量のうち大事なのは$$ G_{\mu\nu},T_{\mu\nu},g_{\mu\nu}, u_\mu$$
の4種類のみです。その都度また説明します。

アインシュタインの縮約記法と言って、同じ添字が上と下に両方現れた場合、その添字について0から3まで総和を取ります。

$$ A^\mu B_\mu \equiv \sum_{\mu=0}^{3} A^\mu B_\mu = A^0 B_0 + A^1 B_1 + A^2 B_2 + A^3 B_3 $$

時刻とスケール因子

宇宙の始まりを $t=0$、現在時刻を $t=t_0$ とします。
また、$a(t)$ という宇宙の広さの尺度を表すスケール因子を導入します。
$$ a(0)=0, a(t_0)=1$$
というふうに定め、宇宙の広さを規格化します。

$a(t)$ が時間とともに大きくなれば、宇宙は膨張していることを意味します。

添え字 $0$ がつく量（後述の$H_0, \Omega_{i0}$ など）は現在時刻での値を表します。

座標の添え字と混同しないようにしてください。

線素と計量

線素$ds^2$ とは、曲がった時空における「(微小)距離の2乗」（三平方の定理の時空版）です。ニュートン力学で「位置」を使って物体の軌跡を記述するのと同様に、一般相対性理論では、時空の形を計量$g_{\mu\nu}$($4\times4$の2階テンソル／行列)で表現します。
線素と計量は次の関係で結ばれています。
$$ ds^2 = g_{\mu\nu} dx^\mu dx^\nu $$
また、一般に計量によって添え字の上げ下げをします。
$$ A_\mu=g_{\mu\nu}A^\nu,A^\mu=g^{\mu\nu}A_\nu $$
ここで$g^{\mu\nu}$は$g_{\mu\nu}$の逆行列です。

特殊相対論でいうミンコフスキー計量
$$ \eta_{\mu\nu}=\rm{diag}(-1,1,1,1)=\begin{pmatrix} -1 & & & \\ & 1 & & \\ & & 1& \\ & & &1 \end{pmatrix} $$
の一般化(座標の取り方の違いによる)だと思えばお気持ちがわかりやすいのではないかと思います。実際、等価原理から、任意の時空点において、一般の計量は座標変換をすれば局所的にミンコフスキー計量に戻せます。
ミンコフスキー時空が定数なのに対し、計量は時空の関数になっていることに気をつけてください。

ここから今から考えようとしているセットアップを紹介します。(公理と書いていますが前提ぐらいの意味だと思ってください)

宇宙モデル(Λ-CDMモデル)

一様平坦宇宙 (曲率$K=0$)
宇宙は物質、放射、ダークエネルギーで均一に満たされ、相互作用はなし

「どこに立っても同じ景色」が見える、シンプルな宇宙です。
物質、放射、ダークエネルギーとは何かは後ほど詳しく説明します。
実は曲率$K=\pm 1$の宇宙を考えることもできますが、実際の宇宙は観測からほぼ曲率がないことを知っているので、今回は扱わないことにします。

座標系

宇宙時間 $t$ と共動(極)座標 $(r, \theta, \phi)$で宇宙全体の座標系を張ります。
$$ x^\mu=\begin{pmatrix} t& r& \theta& \phi \end{pmatrix}^T $$
宇宙時間：全宇宙で一様に流れる時間。私たちが普通に感じる時間です。
共動(極)座標：宇宙と一緒に膨張する座標系。

風船の上に描いた点は、風船が膨らんでも座標値（緯度・経度）は変わりませんが、点同士の物理的な距離は離れていきます。この「座標値」が共動座標です
共同座標のイメージ(a(t)は前述のスケール因子)

第1章：時空を記述する言葉

アインシュタイン方程式

宇宙の時空のダイナミクスは、一般相対性理論のアインシュタイン方程式によって記述されます。
$$ \underbrace{G_{\mu\nu}}_{\text{時空の曲がり}} = 8\pi G \underbrace{T_{\mu\nu}}_{\text{物質の分布}}-\underbrace{\Lambda g_{\mu\nu}}_{\text{宇宙項}} \equiv 8\pi G \, T'_{\mu\nu} $$

この式は「物質が時空を歪める」ことを意味します。これは計量 $g_{\mu\nu}$ に関する10元連立非線形2階偏微分方程式です。

アインシュタイン方程式に登場する物理量

$$ G_{\mu\nu} \equiv R_{\mu\nu} - \frac{1}{2}g_{\mu\nu}R $$

$$ T_{\mu\nu} \equiv (\rho + p)u_\mu u_\nu + p g_{\mu\nu} $$

$G_{\mu\nu}$: アインシュタインテンソル。時空の幾何学（曲がり具合）を表します。
$T_{\mu\nu}$: エネルギー運動量テンソル。宇宙にある物質と放射のエネルギーの分布を表します。
$\Lambda$: 宇宙定数。ダークエネルギーに対応します。（これの意味は後ほど解説します）
$g_{\mu\nu}$:FLRW計量（すぐ後に定義します。）
$\rho$: 物質と輻射のエネルギー密度、$p$: 物質と輻射の圧力、$u_\mu$: 4元速度（$u_\mu u^\mu = -1$ を満たす）

アインシュタインテンソルの構造

$G_{\mu\nu} $ってなんやねんって思いますが、実はこれの定義が本当にややこしいです。

$$ \begin{cases} G_{\mu\nu} \equiv R_{\mu\nu} - \frac{1}{2}g_{\mu\nu}R = 8\pi G T_{\mu\nu} & \text{(アインシュタイン方程式)}\\[8pt] R \equiv g^{\mu\nu}R_{\mu\nu} & \text{(スカラー曲率)}\\[8pt] R_{\mu\nu} \equiv \partial_\lambda\Gamma^\lambda_{\mu\nu} - \partial_\nu\Gamma^\lambda_{\mu\lambda} + \Gamma^\sigma_{\mu\nu}\Gamma^\lambda_{\sigma\lambda} - \Gamma^\sigma_{\mu\lambda}\Gamma^\lambda_{\sigma\nu} & \text{(リッチ曲率)}\\[8pt] \Gamma^\lambda_{\mu\nu} \equiv \frac{1}{2}g^{\lambda\sigma}(g_{\mu\sigma,\nu} + g_{\nu\sigma,\mu} - g_{\mu\nu,\sigma}) & \text{(クリストッフェル記号)} \end{cases} $$
本当にアインシュタインテンソルの形を求めようとするなら、 $g_{\mu\nu}$ → $\Gamma^\lambda_{\mu\nu}$ → $R_{\mu\nu}$ → $R$ → $G_{\mu\nu}$の順番で順次計算していかないといけません。これが相当だるいのです。

これらのテンソルは全て、添字 $\mu,\nu$ を入れ替えても値が変わりません（対称テンソル）。
本記事では、この複雑な計算は割愛し、結果であるフリードマン方程式から議論を始めます。
シュワルツシルト計量という一番簡単なブラックホールの解も同様にこの方程式から導かれるのですが、その計算の流れをわかりやすく理解できるポスターを2025年の五月祭で作成しました。頑張ったのでぜひ見てみて欲しいです。

FLRW計量

FLRW計量（平坦宇宙 $K=0$）

「宇宙原理」（宇宙は大きなスケールで見ればどこも一様で等方である）に基づくと、時空の計量（線素）は以下のFLRW計量（Friedmann-Lemaître-Robertson-Walker metric）で与えられます。
$$ ds^2 = -dt^2 + a(t)^2 (dr^2 + r^2 d\theta^2 + r^2 \sin^2\theta d\phi^2) $$
$$i.e.\quad g_{\mu\nu}=\textrm{diag}(-1,a^2,(ar)^2,(ar\sin\theta)^2) $$

$a(t)$はscaleで述べたスケール因子です。
括弧内は単なる極座標の計量です。空間がスケール因子に従って大きさが変化しているというイメージですね。
一般に曲率$K=\pm1$に対しては$g_{22}=\frac{a^2}{1-Kr^2}$というふうに書けることが知られています。それぞれの時空は下のような形をしています。
宇宙の形
($\Omega_0$を$K+1$と読み替えてください)

エネルギー運動量テンソルの具体形

宇宙を満たす成分は一様等方性より、巨視的には完全流体(エネルギー密度や圧力が全空間で一様、特別な方向の応力がない)として扱えます。

前節で定義した完全流体のエネルギー運動量テンソル $T_{\mu\nu} $ を、FLRW宇宙で評価してみましょう。

流体は宇宙時間 $t$ に対して静止しているため、4元速度は $u^\mu = (1, 0, 0, 0)$ です。
一般形 $T'_{\mu\nu} = (\rho + p)u_\mu u_\nu + (p-\frac{\Lambda}{8\pi G}) g_{\mu\nu}$ に $u^\mu = (1, 0, 0, 0)$ を代入すると、

$$ T'_{\mu \nu} = \text{diag}(-\rho_{tot},a^2 p_{tot},(ar)^2 p_{tot}, (ar\sin\theta)^2p_{tot}) $$

エネルギー密度と圧力

$$ \rho_{tot} \equiv \rho_m + \rho_r + \rho_\Lambda, \quad p_{tot} \equiv p_m + p_r + p_\Lambda $$

物質及び輻射の寄与: $\rho \equiv \rho_m +\rho_r,\,p \equiv p_m + p_r$
ダークエネルギーの寄与: $\rho_\Lambda \equiv \frac{\Lambda}{8\pi G}, \ p_\Lambda \equiv -\frac{\Lambda}{8\pi G}$

eineqで、宇宙項を$T_{\mu\nu}$の一部とみなすのが、宇宙定数をダークエネルギーと対応させたことに当たります。
何故それを「ダークエネルギー」と呼ぶかはもうすぐわかります。

フリードマン方程式

アインシュタイン方程式にFLRW計量と完全流体を代入すると、以下の2つの独立な方程式が得られます。

フリードマン方程式

第1フリードマン方程式（エネルギー制約）:
$$ H^2 = \left( \frac{\dot{a}}{a} \right)^2 = \frac{8\pi G}{3} \rho_{tot} $$

第2フリードマン方程式（加速方程式）:
$$ \frac{\ddot{a}}{a} = -\frac{4\pi G}{3} (\rho_{tot} + 3p_{tot}) $$

一般相対性理論の式から出てくるのはこの2式のみです。

ハッブルパラメータ

$$ H(t) \equiv \frac{\dot{a}(t)}{a(t)} $$

これは宇宙の膨張率を表します。$\dot{a}$ は $a$ の時間微分です。

現在の値 $H_0$ をハッブル定数と呼びます。
ある銀河までの距離を $d$、その銀河の後退速度を $v$ とすると、ハッブル・ルメートルの法則が成り立ちます：
$$ v = H_0 d $$
これは1920年代に発見された、宇宙膨張を示す観測的証拠です。
現在の観測値: $H_0 \approx 67.4 \ \text{km/s/Mpc}$ （プランク衛星2018年）

さらに、エネルギー保存則（$\nabla_\mu T^{\mu\nu} = 0,\,\nabla_\mu$は共変微分）から、各成分ごとの連続の式（局所エネルギー保存則）が導かれます。

連続の式（局所エネルギー保存則）

$$ \dot{\rho}_i + 3H(\rho_i + p_i) = 0 \quad (i = m, r, \Lambda) $$

相互作用がないと仮定したので、各成分ごとに成り立ちます（3本の方程式）。

方程式の個数

第1フリードマン方程式に連続の式を代入すれば、第2フリードマン方程式が導かれるので、一つの方程式は従属です。

そして、各成分の性質を決める状態方程式を仮定します。

状態方程式

$$ p_i = w_i \rho_i　\quad (i = m, r, \Lambda) $$

$w_i$ を状態方程式パラメータと呼びます。

これで3本の方程式が追加されます。

未知変数7個（$a, \rho_m, \rho_r, \rho_\Lambda, p_m, p_r, p_\Lambda$）に対して、独立な方程式7本（フリードマン方程式1本 + 連続の式3本 + 状態方程式3本）がこれで揃いました。
したがって、この系は原理的に解けます！

第2章：宇宙の歴史を紐解く

加速膨張の条件

まず、friedmanの第2フリードマン方程式から、宇宙が加速膨張する条件を導けます。

加速膨張の条件

加速膨張（$\ddot{a} > 0$）するためには：
$$ \frac{\ddot{a}}{a} = -\frac{4\pi G}{3} \rho_{tot} (1+3w) > 0 $$
$$ 1+3w < 0 \quad \Leftrightarrow \quad w < -\frac{1}{3} $$

これが2011年のノーベル賞級の発見（Ia型超新星観測による加速膨張の発見）の理論的背景です。

各成分の状態方程式

まず、連続の式と状態方程式を組み合わせて、各成分のエネルギー密度がスケール因子 $a$ とどう関係するかを導きます。

連続の式 $\dot{\rho}_i + 3H(\rho_i + p_i) = 0$ に $p_i = w_i \rho_i$ を代入すると：

$$ \dot{\rho}_i + 3\frac{\dot{a}}{a}\rho_i(1+w_i) = 0 $$

これを解くと $\rho_i \propto a^{-3(1+w_i)}$ が得られます。

宇宙の3成分とその振る舞い

1. 物質（Matter, m）：水素、冷たいダークマター（Cold Dark Matter）など、
非相対論的な粒子

$$ w_m = 0 \quad \Rightarrow \quad \rho_m \propto a^{-3} $$

体積が広がるにつれて密度が薄まる、直感的な振る舞いですね。
ここでいきなり出てきた「冷たいダークマター」ですが、これは重力相互作用するということしかわかっていない未知の粒子のことを指します。
銀河の回転速度や宇宙背景放射（CMB）、音響バリオン振動（BAO）などの観測的証拠から、その存在はほぼ確実視されています。しかもその(エネルギー)量は、周期表に載っているような通常の元素に比べて5倍も多いことがわかっています。

2. 放射（Radiation, r）：光子（宇宙マイクロ波背景放射 CMB）（、ニュートリノ）など、相対論的な粒子
統計力学より $p = \rho/3$。

$$ w_r = \frac{1}{3} \quad \Rightarrow \quad \rho_r \propto a^{-4} $$

体積による希釈 $a^{-3}$ に加え、宇宙膨張による波長の引き伸ばし（赤方偏移）でエネルギーが $a^{-1}$ 下がるためです。

3. ダークエネルギー（Dark Energy, $\Lambda$）：宇宙定数
eneより

$$ w_\Lambda = -1 \quad \Rightarrow \quad \rho_\Lambda \propto a^0 = \text{const} $$

ここで初めて、宇宙定数がacceを満たすため、ダークエネルギーの一種だと解釈できる理由がわかりましたね。
宇宙が膨張しても薄まらない不思議なエネルギーです。なのでダークエネルギーは、空間に内在する真空エネルギーなのではないかと考えられています。が、そうすると宇宙定数問題という未解決問題が残されます。

状態方程式パラメータの詳細な導出は、外部の解説Webサイトを参考にしてください。

宇宙論パラメータ

臨界密度と密度パラメータ

臨界密度：
$$ \rho_{c} \equiv \frac{3H^2}{8\pi G} $$
密度パラメータ ：
$$ \Omega_{i} \equiv \frac{\rho_{i}}{\rho_{c}} \quad (i = m, r, \Lambda) $$

friedmanの第1フリードマン方程式を両辺$H^2$で割り、密度パラメータで書き直すと
$$\boxed{\Omega_{r} + \Omega_{m} + \Omega_{\Lambda} = 1}$$平坦な宇宙（$K=0$）ではこの式が常に成り立ちます。従って、$\Omega_{i}$ は「宇宙全体のエネルギーのうち、成分 $i$ が占める割合」を表します。

宇宙論パラメータ

観測で得られる$(H_0,\, \Omega_{i,0} )\, (i=m, r, \Lambda (, K)) $が(以上の方程式の境界条件となって)宇宙モデルを決定します。これらの値を宇宙論パラメータと呼びます。
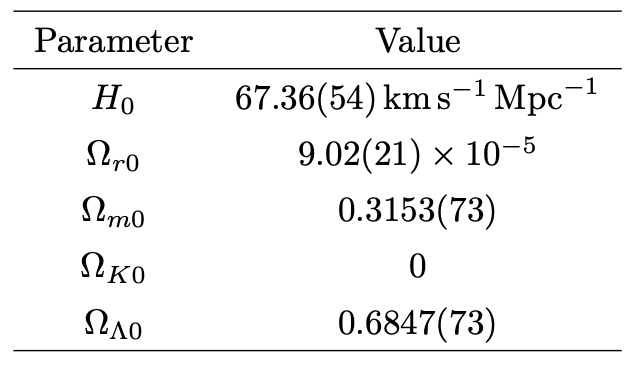宇宙論パラメータ
(『宇宙論の物理(上)』より)

宇宙論パラメータの時間発展

friedmanの第1式に宇宙論パラメータを代入して
$$ H(a) = H_0\sqrt{\frac{\Omega_{r,0}}{a^4} + \frac{\Omega_{m,0}}{a^3} + \Omega_{\Lambda,0}} $$
また、任意の時刻での宇宙論パラメータは合計が1になるので規格化をして、
$$ \Omega_i(a)=\frac{\Omega_{i,0}a^{-(1+w_i)}}{\Omega_{r,0}a^{-4}+\Omega_{m,0}a^{-3}+\Omega_{\Lambda,0}}$$

これで、現在の観測値 $\Omega_{i,0}$ を使えば、任意の時刻(スケール)での宇宙論パラメータ $(H(a),\Omega_i(a))$ が分かるようになりました。
自分たちの宇宙の
密度パラメータの時間変化
(もう時を巻き戻せたもん同然)

第3章：138億年の時を遡る

いよいよ本題です。「宇宙の時間を巻き戻す」計算を実行しましょう。

宇宙の年齢

ハッブルパラメータの定義 $H = \dot{a}/a$ より、$dt = \frac{da}{a H(a)}$ と書けます。

宇宙の年齢 $t_0$ は、ビッグバン（$a=0$）から現在（$a=a_0=1$）までの積分で求められます。

宇宙時刻

\begin{align*} t(a) &= \int_0^{t} dt' = \int_0^{a} \frac{da'}{a' H(a')}\\ &= \frac{1}{H_0} \int_0^a \frac{da'}{\sqrt{\Omega_{r,0} a'^{-2} + \Omega_{m,0} a'^{-1} + \Omega_{\Lambda,0} a'^2}} \end{align*}

この積分は一般には解析的に解けませんが、数値積分で計算できます。
スケール因子の時間発展

各成分の優勢期の解析解

宇宙の歴史の中で、ある成分のみが支配的な時期では、近似を行えばなんとこの積分は解析的に解けてしまいます。

高校の範囲でもできるのでぜひ挑戦してみてください。

放射優勢期（初期宇宙、$\Omega_r \approx 1$）:
$$ a(t)=\sqrt{2H_0\Omega_{r,0}t}\propto t^{1/2} $$

物質優勢期（中期宇宙、$\Omega_m \approx 1$）:
$$ a(t) =\left(\tfrac{3}{2}H_0\sqrt{\Omega_{m,0}}t\right)^{2/3}\propto t^{2/3} $$

物質 → ダークエネルギー遷移期(現在、$\Omega_m +\Omega_\Lambda\approx 1$)

$$\boxed{a(t)=\left(\frac{\Omega_{m,0}}{\Omega_{\Lambda,0}}\right)^{1/3}\sinh^{2/3}\Big(\tfrac{3}{2}H_0\sqrt{\Omega_{\Lambda,0}}t\Big)}$$
ダークエネルギー優勢期（未来、$\Omega_\Lambda \approx 1$）:
$$ a(t) =\left(\frac{\Omega_{m,0}}{4\Omega_{\Lambda,0}}\right)^{1/3}\exp\left(H_0\sqrt{\Omega_{\Lambda,0}}t\right)\propto e^{H_0 t} $$

宇宙の年齢

現在の観測値(para)より$ \Omega_{m,0} \approx 0$なので、物質→ダークエネルギー遷移期の解析解がほぼ厳密解とみなせます。
$t=t(a)$と逆解きして、$a=1,\,\Omega_{m,0} = 1-\Omega_{\Lambda,0} $を代入すれば、
$$ t_0 = \frac{1}{3H_0\sqrt{\Omega_{\Lambda,0}}} \ln\left(\frac{1+\sqrt{\Omega_{\Lambda,0}}}{1-\sqrt{\Omega_{\Lambda,0}}}\right)$$

現在の観測値(para)を代入して計算すると、

$$ \boxed{t_0 \approx 13.8 \text{ Gyr} = 138 \text{億年}} $$

これが、よく聞く「宇宙の年齢138億年」の正体です！
宇宙の年齢がこんなにシンプルな一本の式で表せたのすごくないですか！？

宇宙の広さ（Particle Horizon）

「観測可能な宇宙の半径」とは、宇宙誕生から現在までに光が到達できる最大距離のことです。これを粒子の地平線（Particle Horizon）と呼びます。

光は $ds^2=0$ （ヌル測地線）を進むので、動径方向のみを考えると：

$$ dt = a(t) dr \quad \Rightarrow \quad dr = \frac{dt}{a(t)} $$

粒子の地平線（Particle Horizon）

共動距離 $r_p$ は：

$$ r_p(t) = \int_0^{t} \frac{dt'}{a(t')} = \int_0^{a} \frac{da'}{a'^2 H(a')} $$

ある点に影響できる因果関係の球面半径を意味します。

私たちが観測する物理的な距離（固有距離） $d_p$ は、これに現在のスケール因子 $a(t)$ を掛けたものです。

$$ d_p(a(t)) = a \cdot r_p = a\int_0^{a} \frac{da'}{a'^2 H(a')} $$

風船の表面を這う蟻をイメージしてください。蟻が歩いている間に風船が膨らむと、スタート地点はどんどん遠くなりますよね。
直感で考えていた宇宙の広さ(蟻視点で歩いた距離)は、実は共動距離のこと指していて、本当の広さ(「神」視点で蟻が歩いた距離)というのはそれにスケール因子を掛ける必要があったのです。

現在の宇宙論パラメータで書き直し、$a=1$を代入すると、

$$ d_{p,0} = \frac{1}{H_0} \int_0^1 \frac{da}{\sqrt{\Omega_{r,0} + \Omega_{m,0} a + \Omega_{\Lambda,0} a^4}} $$
この積分を数値計算すると：

$$ \boxed{d_p(t_0) \approx 46.2 \text{ Gly} = 462 \text{億光年}} $$

なぜ138億光年ではないのか？

この記事で一番最初に考えた問題に立ち返りましょう。「宇宙の年齢138億年」なら、光がまっすぐ進んだ距離は「138億光年」のはずでは？

答え：光が旅をしている間にも、背後の空間がどんどん膨張してしまうため、到達距離が伸びる。

第4章：シミュレーションで見る宇宙の一生

数式だけではイメージしにくいかもしれません。そこで、実際に宇宙の時間を巻き戻して、過去の宇宙がどのような大きさだったか、地平線がどう変化するかを視覚的に確認できるシミュレーションを作成しました。

以下のリンクから、スライダーを動かして時間を巻き戻してみてください。

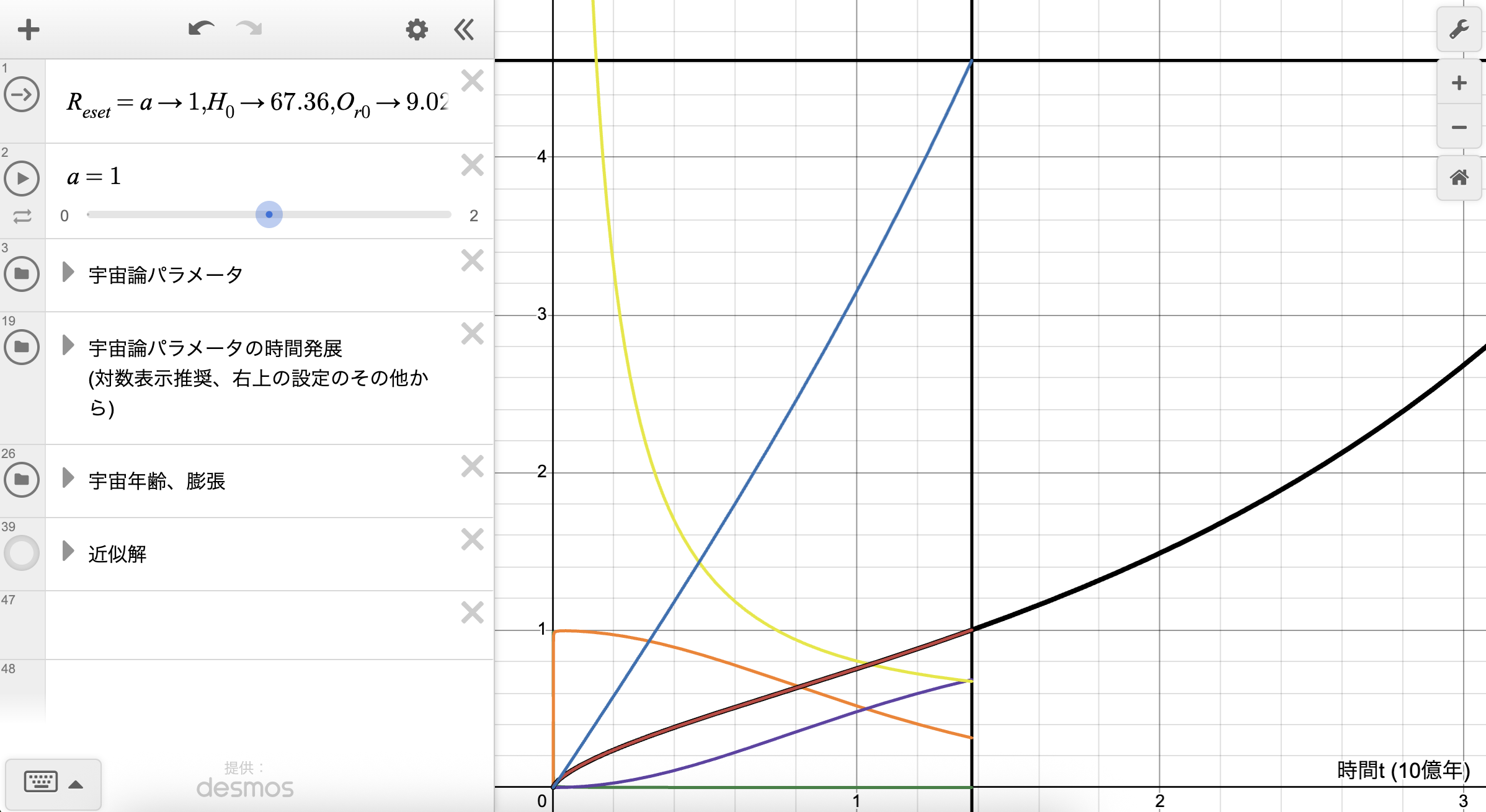Desmosシミュレーション: 宇宙の時間を巻き戻す方法

Desmosシミュレーション

動画を記事に載せられなかったのですが、リンクを踏めば動くのが見れます。

操作方法

スライダーでスケール因子 $a$ や宇宙論パラメータを操作できます。横軸は時間（単位:100億年）に変換してあります。
1行目の$R_{eset}$ボタンを押せば、自分たちの宇宙のパラメータに初期化できます。

$a(t)$ （赤、黒線）: スケール因子
$d(t)$（青線）: 観測可能な宇宙の半径(単位:100億光年)。
$H(t)$（黄線）：ハッブルパラメータ(単位:100km/s/Mpc)
$O_{i}(t)$($r$→緑、$m$→オレンジ、$\Lambda$→紫)：密度パラメータ

現在の $t \approx 13.8$ Gyr 付近では、$a(t)$ のグラフが下に凸になっており、加速膨張している様子が見て取れます。
時間を巻き戻すと、宇宙がどんどん小さくなり、最初からずっと光速よりも速く膨張していたことも分かります。

第5章：別の運命を辿った宇宙たち

私たちの宇宙だけでなく、もしパラメータが違っていたらどのような宇宙になっていたかも比較してみましょう。

様々な宇宙モデル

色んな宇宙のスケール因子の時間発展
（ピンクが私たちの宇宙、現在時刻を$t=0$としている）
1. 物質のみの宇宙（Einstein-de Sitter宇宙）

$$ \Omega_{m,0}=1, \quad \Omega_{\Lambda,0}=0 $$

膨張は減速し続け、永遠に広がり続けますが、加速はしません（$a \propto t^{2/3}$）。

2. 物質過多の宇宙（閉じた宇宙）

$$ \Omega_{m,0} > 1 $$

重力が強すぎるため、膨張はいずれ止まり、収縮に転じて「ビッグクランチ」で終わります。

3. 開いた宇宙

$$ \Omega_{m,0}<1 $$

全密度が臨界密度を下回るため空間曲率が負となり、膨張は減速しますが、収縮に転じることはなく、永遠に広がり続けます。

4. 私たちの宇宙（$\Lambda$-CDM宇宙）

$$ \Omega_{m,0} \approx 0.31, \quad \Omega_{\Lambda,0} \approx 0.69 $$

現在は加速膨張中。未来は指数関数的に膨張し続けます（$a \propto e^{H_0 t}$）。

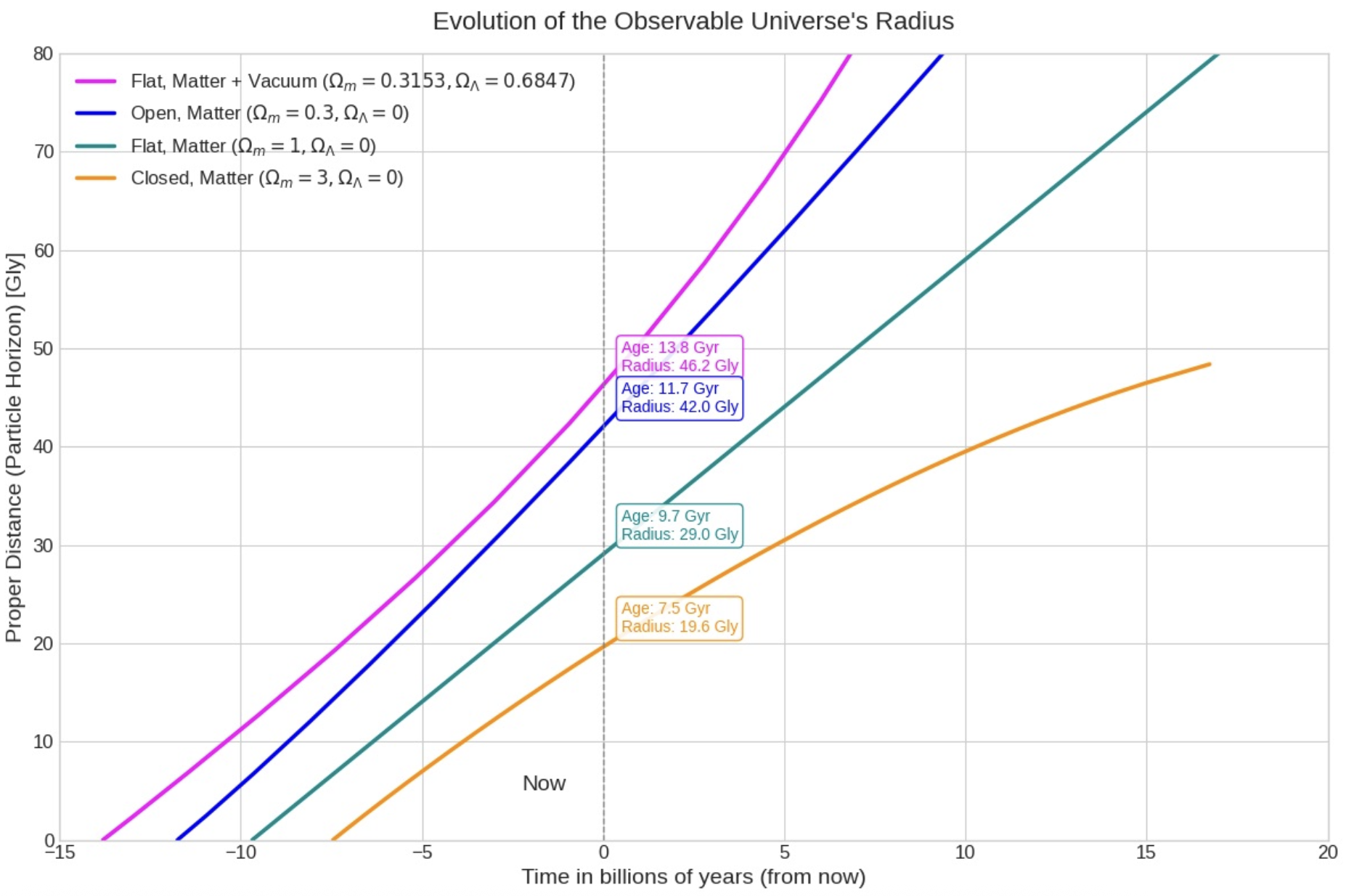色んな宇宙の広がり方

Desmosのシミュレーションでパラメータをいじってみると、これらの宇宙の運命の違いを体験できます。
私たちの宇宙が絶妙なバランスの上に成り立っていることが実感できるでしょう。

おわりに

本記事で分かったこと

一般相対性理論のアインシュタイン方程式(eineq)にFLRW計量(flrw)を代入して得られるフリードマン方程式(friedman)を解くことで：

宇宙の年齢:
$$ t_0 = \frac{1}{3H_0\sqrt{\Omega_{\Lambda,0}}} \ln\left(\frac{1+\sqrt{\Omega_{\Lambda,0}}}{1-\sqrt{\Omega_{\Lambda,0}}}\right) \approx 13.8 \text{ Gyr} $$
観測可能な宇宙の半径:
$$ d_{p,0} = \frac{1}{H_0} \int_0^1 \frac{da}{\sqrt{\Omega_{r,0} + \Omega_{m,0} a + \Omega_{\Lambda,0} a^4}} \approx 46.5 \text{ Gly} $$

わずかハッブル定数 $H_0$ と密度パラメータ $\Omega_{m,0}, \Omega_{\Lambda,0}$ だけで、宇宙の年齢と広がりが計算できてしまうのです。

光が旅をしている間に、その背後の空間がどんどん膨張する——風船の表面を這う蟻のように。だから、光が138億年かけて進んだ先は、気づけば465億光年彼方になっているのです。

私たちの宇宙は、物質とダークエネルギーの絶妙なバランスの上で加速膨張を続けています。Desmosのシミュレーションで時間を巻き戻せば、ビッグバンから現在まで、そして遠い未来へと続く宇宙の物語が目の前に広がります。

夜空を見上げるとき、その暗闇の向こうに広がる465億光年の時空を思い浮かべてみてください。私たちは数式という望遠鏡を手に入れ、宇宙の時間を自由に旅することができるようになったのです。