文献あり

【初投稿】フェルマーの発見と楕円曲線について

360

この著者は初心者として投稿しています。間違いや考慮が足りていない点が含まれている可能性が高いです。見つけたらコメント欄で優しく指摘してあげましょう。

自己紹介

数学コアラです！初投稿なので，簡単に自己紹介させていただきます
・国立大学の数学科学部4年男
・専門は整数論（まだどの分野になるかは分かりません）
・現在はゼミで「数論Ⅰ Fermatの夢と類体論」数論を読んでいます
・雪江先生の整数論１を3年生のときに読んだので，今年の目標は整数論２を読破することです
・数学が得意！というよりは，数学が好き！というタイプです

記事の目的

この記事では，「数論Ⅰ」数論のなかで詳しく説明されなかった，フェルマーの発見と楕円曲線の2倍公式の関係について，できるだけかみ砕いて説明します
難しい大学数学の知識は使わない(写像の話だけ少し出てきます)ので，高校生の方にでも読めると思います！

多くの方に楕円曲線と整数論の繋がりを感じていただけたら幸いです！

※本記事の多くの箇所で，加藤・黒川・斎藤の「数論Ⅰ Fermatの夢と類体論」数論の書き方を参考にします
この記事を読んで興味がわいたら，ぜひ手に取ってみて下さい！

はじめに

タイトルに「フェルマーの発見」と書きましたが，それは次のことを指しています

フェルマーの発見①

三辺の長さが有理数である直角三角形があるとき，それと同じ面積を持つ，三辺の長さが有理数の直角三角形を無限に作り出せる

これは，フェルマーがディオファントスの「数論」の余白に書いた，23番目のコメントらしいです

例えば，辺の長さが $3 ， 4 ， 5$ の直角三角形について考えてみると，この面積は $6$ なので，他にも有理数を三辺に持っていて面積が $6$ になる直角三角形が存在する！ということになります
実際に， $(\frac{7}{10}, \frac{120}{7}, \frac{1201}{70})$ はこれを満たしていることが簡単に確認できるはずです

さて，ここで次の集合を導入します

$A_{d} = {(x, y, z) \in Q^{3} ∣ x^{2} + y^{2} = z^{2}, \frac{1}{2} x y = d}$

これは，面積が $d$ で三辺が有理数となる直角三角形の辺の長さの集合です

上の命題1が成り立つのは，フェルマーが次の事実を発見したことが由来だとされています

フェルマーの発見②

$(x, y, z) \in A_{d}$ に対して，

$(\frac{2 x y z}{y^{2} - x^{2}}, \frac{y^{2} - x^{2}}{2 z}, \frac{z^{4} + 4 x^{2} y^{2}}{2 (y^{2} - x^{2}) z}) \in A_{d}$
である

よって，一組でも有理数を三辺に持つ直角三角形が見つかれば，あとは上の公式に代入するだけで，
無限に同じ面積をもつ直角三角形を作り出せることになります！（ループして同じ解ばかりになる可能性ってあるのかな）

この公式をフェルマーはどのように思いついたのか、、、、、
この背景に実は，楕円曲線の2倍公式というものが関わっているんです！！！

楕円曲線について

次の形の方程式で与えられる曲線を， $Q$ 上の楕円曲線と呼びます
$y^{2} = a x^{3} + b x^{2} + c x + d, (a, b, c, d \in Q)$
ただし， $a \neq 0$ で右辺の $x$ の3次式は重根を持たないものとします

楕円曲線と楕円はまったくの別物ですので，楕円曲線について知らない方はグラフの形を実際に調べてみてから読み進めていただきたいと思います

これ以降，楕円曲線上の有理数点をターゲットにして話を進めるので，そのためにまず，次の集合を導入します

$C_{d} = {(x, y) \in Q^{2} ∣ y^{2} = x^{3} - d^{2} x, y \neq 0}$

これは， $y^{2} = x^{3} - d^{2} x$ という形の楕円曲線上にある有理数点の集合です
実は，この集合と $A_{d}$ は同型になっていることが確かめられるんです！

フェルマーの発見と楕円曲線の関係

$A_{d} ≅ C_{d}$ である

実際，写像 $f : A_{d} \to C_{d}$ ， $g : C_{d} \to A_{d}$ について，
$\begin{aligned} f (x, y, z) & = (\frac{y (y + z)}{2}, \frac{y^{2} (y + z)}{2}), \\ g (X, Y) & = (\frac{2 X d}{Y}, \frac{X^{2} - d^{2}}{Y}, \frac{X^{2} + d^{2}}{Y}) \end{aligned}$
とおくと， $f (x, y, z) \in C_{d}$ ， $g (X, Y) \in A_{d}$ となり， $(g \circ f) = {id}_{A_{d}}$ ， $(f \circ g) = {id}_{C_{d}}$ が確かめられます
計算は代入して整理して、、、の繰り返しなので本記事では省略しますが，希望があれば別の記事で証明を掲載したいと思います

※「数論Ⅰ」数論では $B_{d} = {(u, v, w) \in Q^{3} ∣ u^{2} + d = v^{2}, v^{2} + d = w^{2}}$ という集合を考え， $A_{d} ≅ B_{d}$ と $B_{d} ≅ C_{d}$ を示すことによって，この定理を証明しています
なんで $A_{d}$ の次が $B_{d}$ じゃなくて $C_{d}$ だったのか，疑問に思った方がいたら，まあそういうことです
写像 $f, g$ がなぜこんな形になるのか，どうしたらそれが求まるのか疑問を感じる方もいると思いますが，そんなときは「数論Ⅰ」数論を参照してください
写像の合成によって，簡単に求めることができます

楕円曲線上の点を2倍にする？？？

曲線上の点を2倍にする，そんなことができるのか疑問に思うかもしれませんが，
実は， $Q$ 上の楕円曲線の有理点 $P, Q$ に関して，和 $P + Q$ というものを定めることができるのです！！！

楕円曲線

E

上の点の和

$P = (x_{1}, y_{1}), Q = (x_{2}, y_{2})$ について， $P$ と $Q$ を結ぶ直線と楕円曲線 $E$ の交点を $P * Q = (x_{3}, - y_{3})$ としたとき， $P + Q = (x_{3}, y_{3})$ と定める

$P = (x_{1}, y_{1})$ と $P$ の和 $P + P = 2 P$ については， $P$ での接線と $E$ の交点を $(x_{3}, - y_{3})$ としたとき， $2 P = (x_{3}, y_{3})$ と定める

上の定義はとても雑で，楕円曲線の群構造にでてくる単位元となる無限遠点 $O$ の話や， $P$ が変曲点で接線が $E$ と交わらない場合の話， $O$ との和の話，逆元の話，結合法則が成り立っている話など，説明が足りていない部分が沢山あります
しかし，本記事の内容を理解する上では，上の内容だけ理解していただけたら大丈夫です！
詳しく知りたい方は，「数論Ⅰ」数論やシルヴァーマンの「楕円曲線論入門」，少し進んだ内容として「楕円曲線と保型形式」楕円を読んでみて下さい
（私も全部読んだわけではないんですが、、、）

言葉だけみても分からないと思いますが，次の図を見れば，何をしているかが分かるはずです

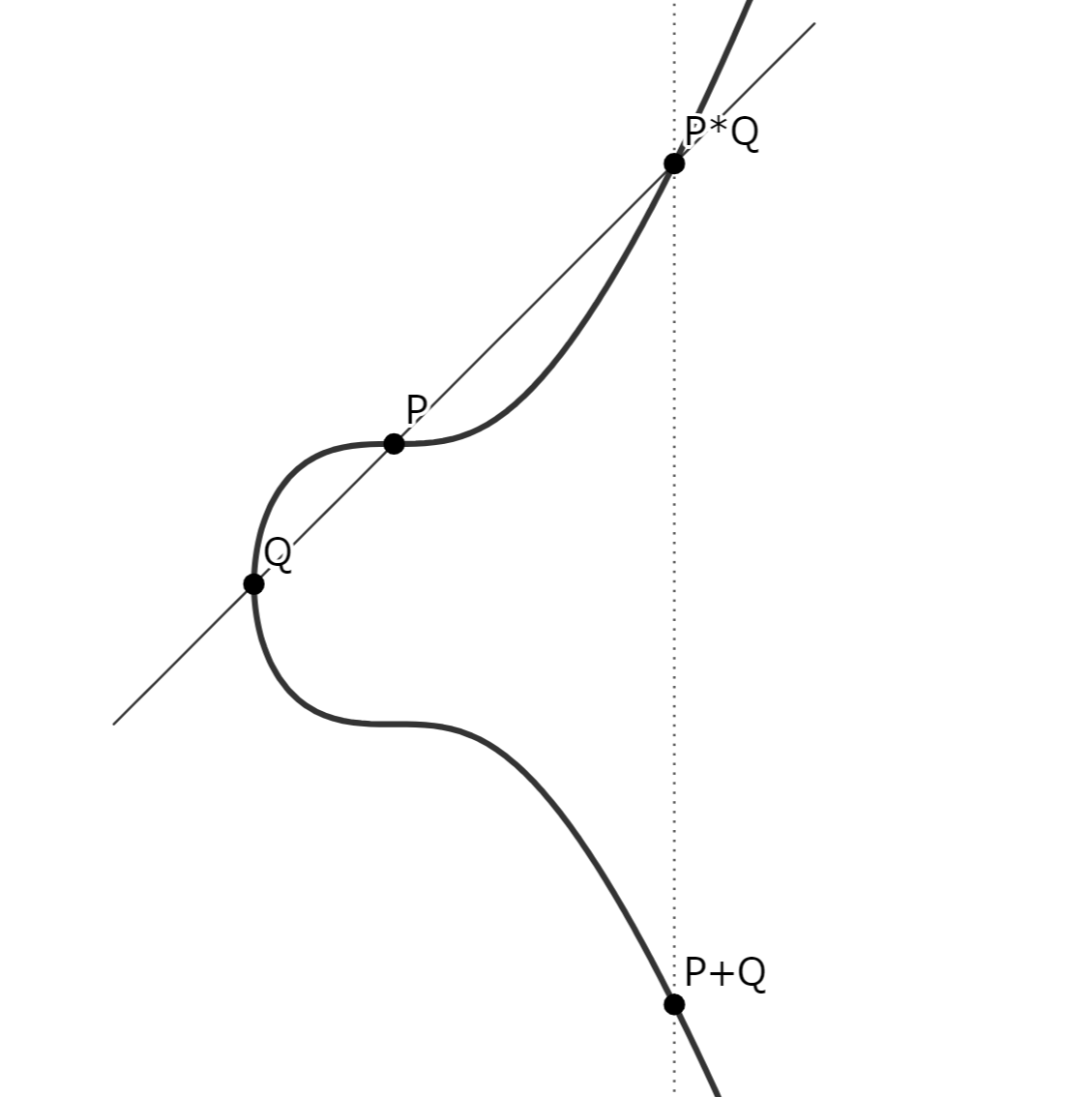楕円曲線の和

異なる2点を通る直線（または1点の接線）と，楕円曲線が交わった点を， $x$ 軸について折り返したところが「和」になっているという感覚で問題ありません

さて，上で定義した和について， $P + Q$ や $2 P$ の座標を求めることは，代入と式の展開，整理を頑張るだけで，簡単に求めることができます（ちょっと大変だけど）
本記事では証明しませんが，これから大事になってくる特別な形の楕円曲線の場合について，和の公式を書いておきます

楕円曲線 $y^{2} = x^{3} - d^{2} x$ 上のゼロでない有理点 $P = (x_{1}, y_{1}), Q = (x_{2}, y_{2})$ について，その和を $P + Q = (x_{3}, y_{3})$ とすると，

$x_{1} \neq x_{2}$ のとき， $λ = \frac{y_{2} - y_{1}}{x_{2} - x_{1}}$ として，
$x_{3} = λ^{2} - x_{1} - x_{2}, y_{3} = λ (x_{1} - x_{3}) - y_{1}$
$x_{1} = x_{2}, y_{1} = y_{2}$ ( $P = Q$ )のとき， $λ = \frac{3 x_{1}^{2} - d^{2}}{2 y_{1}}$ として，
$x_{3} = λ^{2} - 2 x_{1}, y_{3} = 3 x_{1} λ - λ^{3} - y_{1}$

というように座標を計算することができる

ここで，2の式について，本記事では特に楕円曲線の2倍公式と呼ぶことにします
なお，「数論Ⅰ」数論の定め方と全然違うじゃねーか，と気づかれる人もいるかと思いますが，この公式の言っていることは，実際には本の内容と一致していることが確かめられます
この公式を採用したのは，あとの計算が楽になるからです(参考論文：論文)

フェルマーの発見と楕円曲線の2倍公式の関係

上の2倍公式の内容を，先ほど定めた $C_{d}$ を使って言い換えると，次のようになります

楕円曲線の2倍公式

$(x, y) \in C_{d}$ に対して， $λ = \frac{3 x^{2} - d^{2}}{2 y}$ とおけば，
$(λ^{2} - 2 x, 3 x λ - λ^{3} - y) \in C_{d}$
である

なんだか，命題2と似ていますね、、、

実は，この楕円曲線の2倍公式が，命題2の変換と対応していることがわかるんです！！！

フェルマーの発見と楕円曲線の2倍公式

命題2と命題4は，互いに対応した変換になっている

証明は長いので，きつい方は読み飛ばしてもらっても大丈夫です
まだこの主張のすごさにピンと来ていない方は，証明の下にある図を見ていただければ，何かピンとくるものがあるかもしれません！

定理3の証明で使った写像 $f : A_{d} \to C_{d}$ ， $g : C_{d} \to A_{d}$ を利用して計算していきます
計算量は多くなりますが，本記事の主定理となるので，頑張って計算します
写像 $f, g$ について忘れている方もいると思うので，再掲載しておきます
$\begin{aligned} f (x, y, z) & = (\frac{y (y + z)}{2}, \frac{y^{2} (y + z)}{2}), \\ g (X, Y) & = (\frac{2 X d}{Y}, \frac{X^{2} - d^{2}}{Y}, \frac{X^{2} + d^{2}}{Y}) \end{aligned}$
証明の流れとしては，次の通りです

$(x, y, z) \in A_{d}$ に対し， $f (x, y, z) \in C_{d}$ だったので，2倍公式を用いて，この $f (x, y, z)$ を2倍にする
$f (x, y, z)$ を2倍にした点を $f^{'} (x, y, z)$ とおく
$f^{'} (x, y, z) \in C_{d}$ なので， $g (f^{'} (x, y, z)) \in A_{d}$ である
$g (f^{'} (x, y, z))$ が，命題2のフェルマーが発見した公式と一致していることを確かめる

では，順番に証明していきます．

１．命題4を使うために，先に $λ$ について計算しておきます
$\begin{aligned} λ & = \frac{3 \frac{y^{2} (y + z)^{2}}{4} - \frac{x^{2} y^{2}}{4}}{2 \frac{y^{2} (y + z)}{2}} = \frac{3 (y + z)^{2} - x^{2}}{4 (y + z)} = \frac{3 (y + z)^{2} + (y^{2} - z^{2})}{4 (y + z)} = \frac{(3 y^{2} + 6 y z + 3 z^{2}) + (y^{2} - z^{2})}{4 (y + z)} \\ = \frac{4 y^{2} + 6 y z + 2 z^{2}}{4 (y + z)} = \frac{2 y^{2} + 3 y z + z^{2}}{2 (y + z)} = \frac{(2 y + z) (y + z)}{2 (y + z)} = \frac{2 y + z}{2} \end{aligned}$
（ここで， $x^{2} + y^{2} = z^{2}, \frac{1}{2} x y = d$ が成り立つことに注意してください）
これを命題4の式に代入して計算することにより，
$\begin{aligned} f^{'} (x, y, z) の第1成分 & = {(\frac{2 y + z}{2})}^{2} - 2 \cdot \frac{y (y + z)}{2} = \frac{4 y^{2} + 4 y z + z^{2} - 4 y^{2} - 4 y z}{4} = \frac{z^{2}}{4}, \\ f^{'} (x, y, z) の第2成分 & = - {(\frac{2 y + z}{2})}^{3} + 3 \cdot \frac{y (y + z)}{2} \cdot \frac{2 y + z}{2} - \frac{y^{2} (y + z)}{2} \\ = \frac{- 8 y^{3} - 12 y^{2} z - 6 y z^{2} - z^{3} + 12 y^{3} + 18 y^{2} z + 6 y z^{2} - 4 y^{3} - 4 y^{2} z}{8} \\ = \frac{2 y^{2} z - z^{3}}{8} = \frac{(2 y^{2} - z^{2}) z}{8} = \frac{(y^{2} - x^{2}) z}{8} \end{aligned}$
となります

２．上で求めた $f^{'} (x, y, z)$ を写像 $g$ でとばします
$\begin{aligned} g (f^{'} (x, y, z)) & = g (\frac{z^{2}}{4}, \frac{(y^{2} - x^{2}) z}{8}) = (\frac{2 \frac{z^{2}}{4} \frac{x y}{2}}{\frac{(y^{2} - x^{2}) z}{8}}, \frac{\frac{z^{4}}{16} - \frac{x^{2} y^{2}}{4}}{\frac{(y^{2} - x^{2}) z}{8}}, \frac{\frac{z^{4}}{16} + \frac{x^{2} y^{2}}{4}}{\frac{(y^{2} - x^{2}) z}{8}}) \\ = (\frac{2 x y z}{y^{2} - x^{2}}, \frac{z^{4} - 4 x^{2} y^{2}}{2 (y^{2} - x^{2}) z}, \frac{z^{4} + 4 x^{2} y^{2}}{2 (y^{2} - x^{2}) z}) \end{aligned}$
となります

３． $g (f^{'} (x, y, z))$ の第2成分について，
$\begin{aligned} \frac{z^{4} - 4 x^{2} y^{2}}{2 (y^{2} - x^{2}) z} & = \frac{(x^{2} + y^{2})^{2} - 4 x^{2} y^{2}}{2 (y^{2} - x^{2}) z} = \frac{x^{4} + 2 x^{2} y^{2} + y^{4} - 4 x^{2} y^{2}}{2 (y^{2} - x^{2}) z} \\ = \frac{x^{4} - 2 x^{2} y^{2} + y^{4}}{2 (y^{2} - x^{2}) z} = \frac{(y^{2} - x^{2})^{2}}{2 (y^{2} - x^{2}) z} \\ = \frac{y^{2} - x^{2}}{2 z} \end{aligned}$
となるので，
$g (f^{'} (x, y, z)) = (\frac{2 x y z}{y^{2} - x^{2}}, \frac{y^{2} - x^{2}}{2 z}, \frac{z^{4} + 4 x^{2} y^{2}}{2 (y^{2} - x^{2}) z})$
が得られます
これは，命題2のフェルマーが発見した公式と完全に一致していることが分かります
（２の計算は，論文を参考にさせていただきました）

定理5の主張だけでは，一見すごさが感じられないかもしれませんが，
下の図を見ていただけば，この定理が主張するすごさが実感できるかと思います！！！

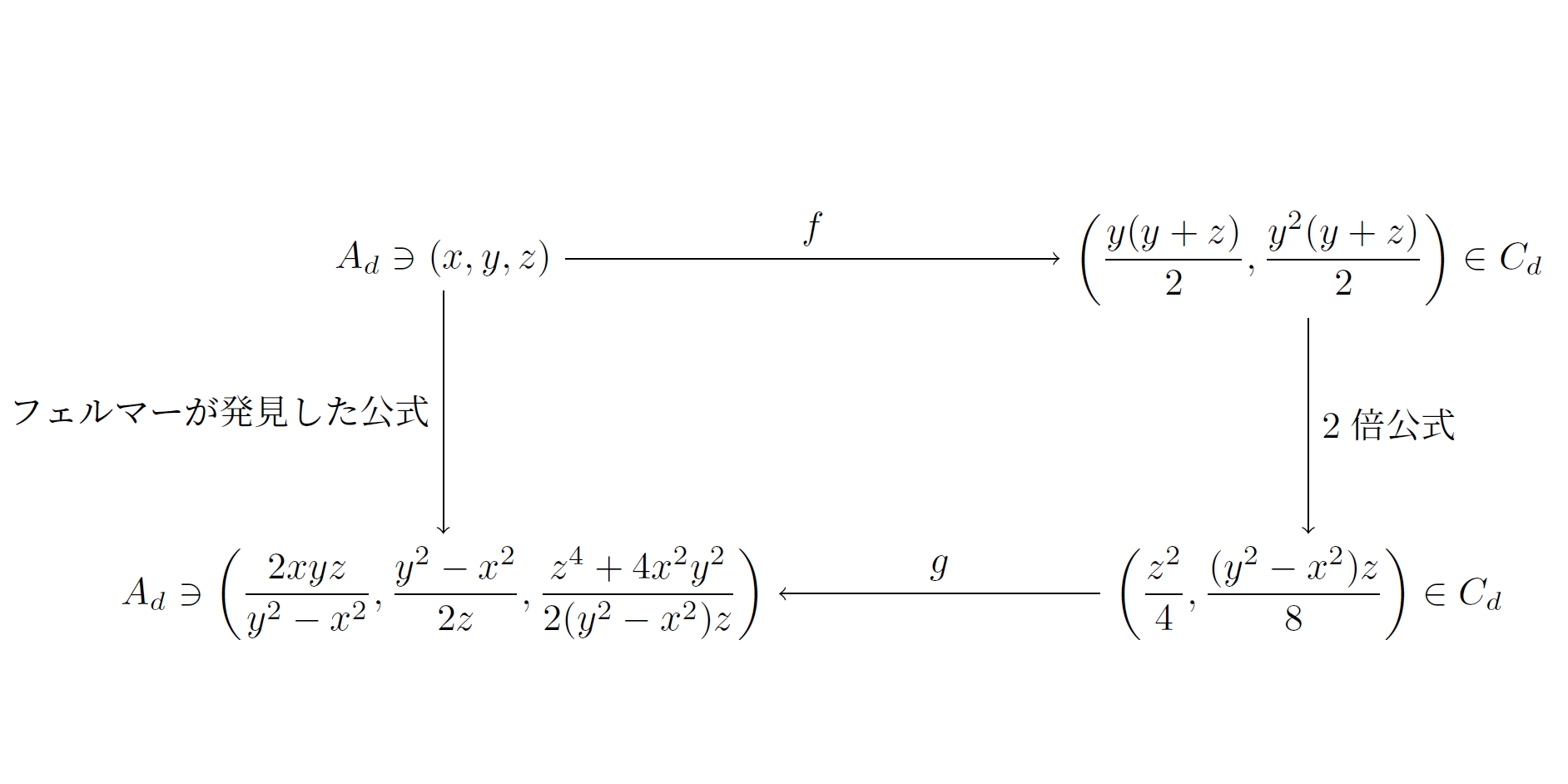
さいごに

命題1で面積として表れる数 $d$ のことを，合同数といい，今もまだどのような数が合同数になるか，という合同数問題は未解決となっています

合同数に関する有名な定理として，Tunnel（タネル）の定理というものがあります
この主張の逆を示すことができれば，合同数問題は解決されるのですが，楕円曲線に関するミレニアム懸賞問題の1つである，Birch-Swinnerton-Dyer（バーチ・スウィンナートン・ダイアー）予想が解決されれば，Tunnelの定理の逆が示されたことになり，合同数問題も解決されることがわかっています

このように，整数論と楕円曲線というのは，本記事のような初等的な内容から未解決問題まで，多岐にわたって関係しているのです

本記事を通して，フェルマーのすごさを感じたり，整数論と楕円曲線との繋がりを少しでも面白いと思っていただけたりしたら幸いです，
ということで私の記事を終わりたいと思います

初投稿でまだまだ未熟なところもあったかと思いますが，最後までお読みいただき本当にありがとうございました！