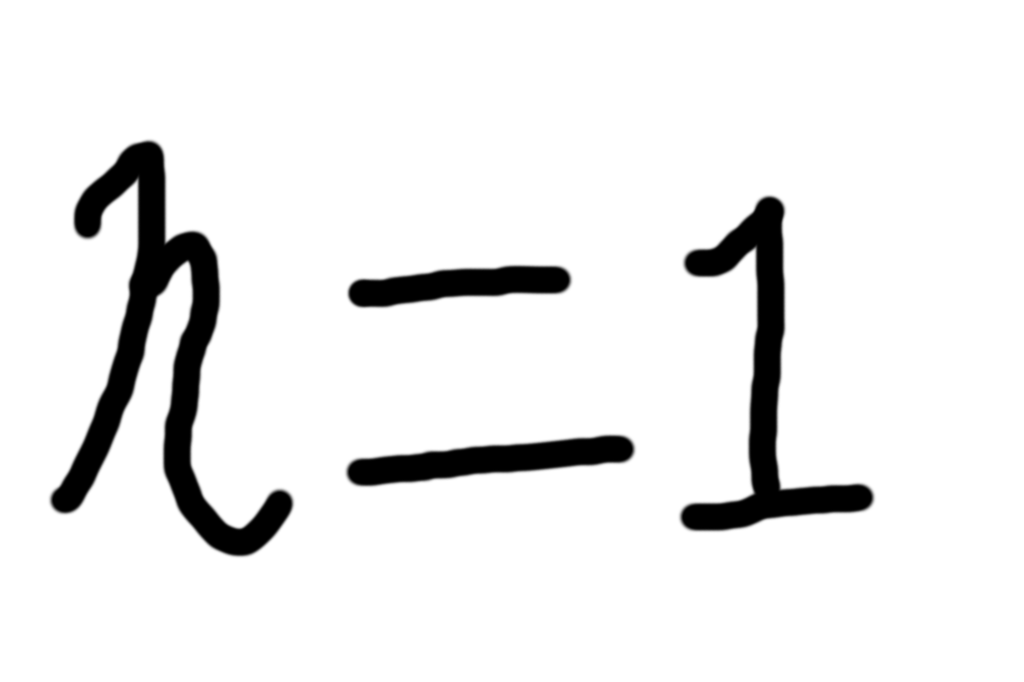差分⋅和分でできないこと

はじめに

　こんにち和、お久しぶりですn=1です。今回は差分⋅和分でできないことについてやっていきます。

記号の説明

　今回の記号は一部 がーと 様の 高校数学の数列と微分積分は似ているという話（和分差分） を使わせていただきます。

差分にできないこと

上の式はシフト作用素$E$を考えた時$\Delta+1=E$で、$g(x)+\underset{x}{\Delta}g(x)=g(x+1)$であることから一つ目の等式が分かり、そこから合成関数の微分のようにできないと分かります。なおこのことから微積分でできたいろいろなことが制限されます。
例1より分数のように扱えないので$\frac{\delta}{\delta x}:=\underset{x}{\Delta}$としても
$$\frac{\delta z}{\delta x}\neq \frac{\delta z}{\delta y}\cdot \frac{\delta y}{\delta x}$$
でUIとしてあまりよくないと考えられます。

同値でないことは$\Delta$の核を考えた時$\underset{x}{\Delta}f(x)=0 \Longleftrightarrow f(x+1)=f(x)$より$$\ker (\Delta)= \lbrace C_1|^{\forall} x [C_1(x+1)=C_1(x)]\rbrace $$と分かりるため、周期関数が出ると分かります。
そして$D$を微分作用素としたとき$\ker(D^{n})=\lbrace \sum_{k=0}^{n-1}a_kx^{k}|^{\forall} a_k \rbrace $または$\ker(D^n)= \lbrace f_{n}|^{\exists}f_{n-1}\in \ker(D^{n-1}),^{\exists}C,^{\forall} x [f_{n}(x)=xf_{n-1}(x)+C] \rbrace $であり、微分方程式は定数項が出ますが、一方差分は$\ker(\Delta^{n})= \lbrace C_{n}|^{\exists}C_{n-1}\in \ker(D^{n-1}),^{\forall}x [C_{n}(x+1)=C_{n}(x)+C_{n-1}(x)] \rbrace $
となり、$A_k$を周期1の関数として$$C_{n}(x)=\sum_{k=0}^{n-1}A_k(x)x^{k}\ \ \ (={\sum}_{0}^{n}A_k(x)x^{k}\delta k)$$と微分方程式のときと似たような形($a_0+a_1x+\cdots +a_{n-1}x^{n-1}$)が出ると分かります。

和分にできないこと

これは通常の置換積分を考えると直ちにわかり、
$$\frac{d}{dt}\int f(x)dx=\frac{d}{dx}\frac{dx}{dt}\int f(x)dx$$
$$\ \ \ \ \\ \ \ \ \ \ \ \ \\ \ \ \ \ \ \ \\ \ \ \ \ \ \ =\frac{d}{dt}(g(t))\frac{d}{dx}\int f(x)dx =f(g(t))\frac{d}{dt}(g(t))$$
と途中に連鎖律を用いていることに由来します。

これは例3の置換和分と同じで、King Propertyは$y=a+b-x$とした置換積分を行った時に得られるため起こります。

最後に

　以上で今回の差分⋅和分でできないことは終わりです。間違っている点、疑問点がありましたらご指摘のほどお願いします。投稿を見てくださりありがとうございました。