ボルツマン分布はなぜ指数関数になるのか -Juliaによる数値計算-

ボルツマン分布はなぜ指数関数になるのか

統計力学でボルツマン分布を勉強した際、抽象度が高く理解に苦しんだ方も少なくないと思います。もしくは、演習問題を解く上でボルツマン分布は使えても、どうしてボルツマン分布が指数関数になるのかを説明するのは難しいと思います。

この文章では、ボルツマン分布に従う系の特徴を捉えたモデルを構築し、数値実験することで指数関数が再現されることを実験的に理解してみたいと思います。あくまで直観的な理解になるので、厳密な証明というよりかは実験的な理解の範疇だと思って頂ければと思います。

理想気体

ボルツマン分布に従う最もシンプルな系は理想気体です。理想気体中の分子は縦横無尽に熱運動しており、各粒子が持っているエネルギーの値はまちまちです。しかし、少ないエネルギーを持つ粒子が系の大多数を占め、大きなエネルギーを持つ粒子はごく少数であろうことは予想できます。理想気体が他の系とエネルギーのやり取りをしない断熱容器に入れられているなら、理想気体の粒子が持つエネルギーの総量は一定だからです。
理想気体のイメージ

エネルギー$\varepsilon $を持つ粒子の数を$N(\varepsilon)$とします。ボルツマン分布によると、逆温度$\beta=\frac{1}{k_B T}$を持つ系では

$$N(\varepsilon) \propto \exp(-\beta\varepsilon) $$

となることが知られています。$N(\varepsilon)$が指数関数になることを理解すべく、理想気体の特徴を考えてみます。

理想気体の特徴（1）：孤立系

上記でも述べましたが、理想気体は外部とエネルギーのやり取りをしない孤立系です。つまり粒子数$N$と総エネルギー$E$は一定の値をとります。そのため、各粒子に総エネルギー$E$が分配されて、一粒子ごとに平均$e = E/N$程度のエネルギーを有することになります。

理想気体の特徴(2):粒子同士は衝突を繰り返す

理想気体の粒子は互いに衝突し合います。その際に、系の構成要素である粒子がエネルギーを授受しあいます。こうして粒子一つ一つが持っているエネルギーに揺らぎが生じ、だんだん粒子の持つエネルギーの値が平均化されていきます。

この点が非常に重要で、ボルツマン分布が登場するカノニカル統計では、系の構成要素同士で弱いエネルギーの相互作用を行います。このような相互作用が生じないのがミクロカノニカル統計、生じるのがカノニカル統計です。

理想気体の特徴(3):(2)を繰り返すと熱平衡状態に至る

粒子同士が衝突する前では、高エネルギーの粒子も低エネルギーの粒子も混在しているかもしれません。しかし、粒子同士の衝突を繰り返すことで、高エネルギーの粒子は低エネルギーの粒子にエネルギーを分け与えるイベントが繰り返し生じます。したがって、(2)が繰り返されると粒子のエネルギーが平均化され続けて熱平衡状態に至ります。熱平衡状態では、高エネルギーの粒子がごくわずかで、低エネルギーの粒子が系の大多数を占めるであろうことが予想できます。

以上をまとめましょう。

モデル化

前節で抽象した理想気体の特徴をモデル化しましょう。

6人で30枚のチップを適当に分配します。次に、6人から無作為に2人選び、片方からもう片方にチップを1枚譲渡します。この操作を何回も繰り返します。持っているチップの枚数でヒストグラムを作成するとどうなるでしょうか。

ただし、チップが0枚の人からはチップを奪いません。借金は無しとします。

理想気体の特徴と比較しましょう

統計的に見るために、この6人グループを100グループ作成します。

コーディング(Julia)

参考文献[1]をコピペリスペクトしました。

      using Plots

#初期状態の作成
function make_initial(numpeople, numchip)
 boxes = zeros(Int64, numpeople)
  for i = 1:numchip
   targetbox = rand(1:numpeople)
   boxes[targetbox] += 1
  end
 return boxes
end

#チップの授受
function giveandtake(oldboxes)
  newboxes = copy(oldboxes)
  numpeople = length(oldboxes)
  A = rand(1:numpeople)
  B = rand(1:numpeople)
  while B == A
   B = rand(1:numpeople)
  end
 #AさんからBさんに渡す。
  if newboxes[A] > 0
   newboxes[A] -= 1
   newboxes[B] += 1
  end
 return newboxes
end

#エントロピーの計算
function calc_entropy(boxes, numchip)
  total = length(boxes)
  S = total*log(total) - length(boxes[boxes .== 0])
  for i = 1:numchip
   num_i = length(boxes[boxes .== i])
    if num_i == 0
     S -= num_i
    else
     S -= num_i * log(num_i)
    end
   end
  return S/total
end

#初期状態のヒストグラム
function test1()
  numpeople = 6
  numchip = 30
  numgroups = 100
  totalpeople = numpeople * numgroups
  totalboxes = zeros(Int64, numgroups, numpeople)

  for i = 1:numgroups
   totalboxes[i,:] = make_initial(numpeople, numchip)
  end
  histogram(totalboxes[:], nbins = -0.5:1:numchip, label = "initial", ylims = (0, totalpeople*0.3))
end

function test2()
  numpeople = 6
  numchip = 30
  numgroups = 100
  totalpeople = numpeople * numgroups
  totalboxes = zeros(Int64, numgroups, numpeople)

  for i = 1:numgroups
   totalboxes[i,:] = make_initial(numpeople, numchip)
  end

  #全グループで、giveandtakeをnumtotal回やる
  numtotal = 500
  for itrj = 1:numtotal
   for i = 1:numgroups
    totalboxes[i,:] = giveandtake(totalboxes[i,:])
   end
  end
  histogram(totalboxes[:], nbins = -0.5:1:numchip, label = "$numpeople-people, $numchip-chips", ylims = (0, totalpeople * 0.3))
  #指数関数を描画
  x = range(0,30,100)
  plot!(x -> 100 * exp(-0.18 * x), lw = 1.5, label = "exponential")
end

#実行
test2()
    

実装結果

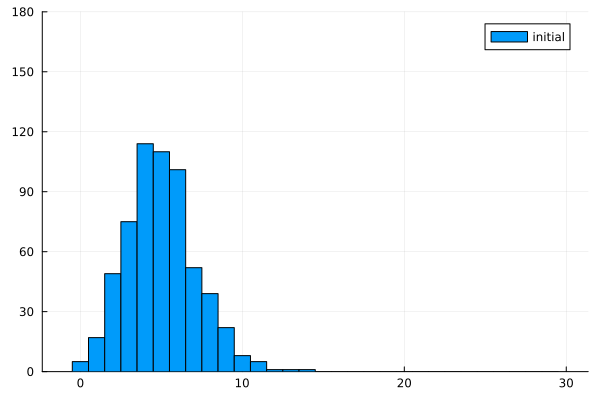初期分布

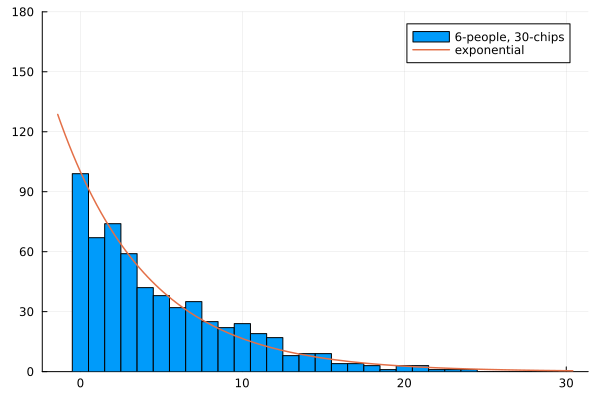チップを500回交換した結果

以上のように、指数関数に非常に近い結果が実験的に導かれていることが確かめられます。このように、チップの授受が可能であることが指数関数を導く鍵になっているようです。

本当はヒストグラム自体を片対数プロットしたかったのですが、試行錯誤してもできなかったので有識者がいればご教授願いたいなと思います。

大雑把な解釈

指数関数的に減少することは、たくさんのチップを有する人の割合が非常に少ないことを表しています。十分量の試行回数があるとき、ある1人がチップを$M$枚増やすためにはM回抽選に選ばれて$1/2$の確率で勝利し続けなければなりません。その勝率は$(1/2)^M$に比例するため、そのような豪運の持ち主は指数関数的に減少するのだと考えられます。

所持チップ数の時間変化を実際に見てみましょう。

      function test4()
  numpeople = 6
  numchip = 30
  numgroups = 100
  numtotal = 600
  totalpeople = numpeople * numgroups
  totalboxes = zeros(Int64, numgroups, numpeople)
  timedepboxes = zeros(Int64, numtotal, numpeople)

  timedepboxes[1,:] = make_initial(numpeople,numchip)
 for itrj = 2:numtotal
  timedepboxes[itrj,:] = giveandtake(timedepboxes[itrj-1,:])
 end
 for i = 1:numpeople
 plot!(timedepboxes[:,i],label = "$i-th")
 end
end
test4()
    

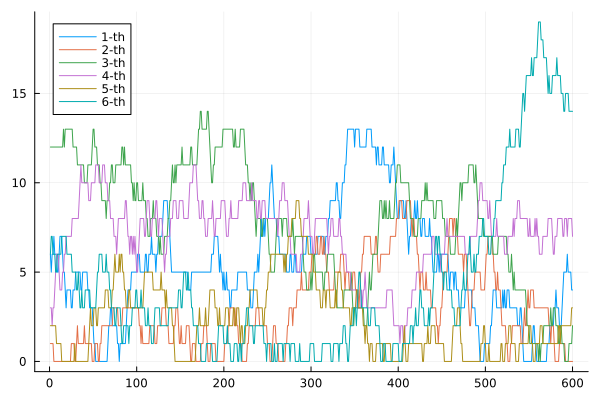6人が所持しているチップの総数

大体の場合には途中でチップを失ってしまいます。この状況を時系列データでプロットすると、一度大富豪になった人が短時間でチップを失う様子が観察されます。筆者は勝手にこの現象を「盛者必衰」と呼んでいます(笑)。

エントロピーによる理解

チップの授受がランダムに生じると、初期分布の情報が失われ、エントロピーが増大していくのではと考えました。そこで、エントロピー増大の視点からボルツマン分布になることを検証していきます。

$N$人でチップ$M$枚を授受したとき、チップが$i$枚の人が$n_i$人いるとします。この系のエントロピーは

$$S = \log(\frac{N!}{n_{1}!\cdots n_{M}!})$$

と表されます。上記の仮説が正しいとすると、繰り返し計算する過程でエントロピーの時間変化が揺らぎながら単調増加する様子が観察されるはずです。以下のコードを実装してみます。

      function test3()
  numpeople = 6
  numchip = 30
  numgroups = 100
  totalpeople = numpeople * numgroups
  totalboxes = zeros(Int64, numgroups, numpeople)

  for i = 1:numgroups
   totalboxes[i,:] = make_initial(numpeople, numchip)
  end

  numtotal = 500
  entropyboxes = zeros(Float64, numtotal)

  for itrj = 1:numtotal
   for i = 1:numgroups
    totalboxes[i,:] = giveandtake(totalboxes[i,:])
   end
    entropyboxes[itrj] = calc_entropy(totalboxes, numchip)
  end
 return totalboxes, entropyboxes
end

s = test3()
plot(s[2], title = "Time series of entropy", xlabel = "time", ylabel = "entropy", label = "entropy", lw = 1.5, ylims = (2,3.5))
savefig("time_series_entropy")
    

実装結果

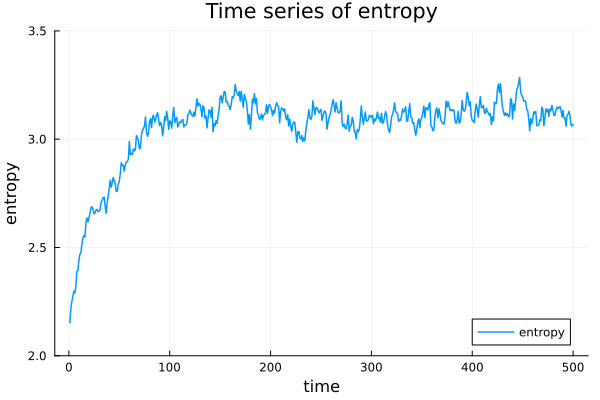エントロピーの時間変化

揺らぎながらも、初期状態から単調増加して、$100$回目くらいで熱平衡状態のような状態に至ることが確かめられました。

エントロピー増大とボルツマン分布

エントロピー増大からボルツマン分布を導いてみましょう。

$$S = \log(\frac{N!}{n_{1}!\cdots n_{M}!})$$

を最大化するのが目標です。スターリングの公式を使って変分を取り、最大値を取る条件$\delta S = 0$を適用すると、

$$\delta S = -\sum_{i = 1}^{M}(\log{n_{i}+1})\delta n_i= 0 \tag{1}$$

になる必要があります。ただし、$n_1, \cdots ,n_{M}$には粒子数、エネルギー量の2種類の拘束条件がかかります。

$$\sum_{i = 1}^{M}n_{i} = N \quad \therefore \sum_{i = 1}^{M}\delta n_i=0 \tag{2}$$

$$\sum_{i = 1}^{M}\varepsilon_{i}n_{i} = E \quad \therefore \sum_{i = 1}^{M}\varepsilon_{i}\delta n_i=0 \tag{3}$$

拘束条件付きの最大化にはLagrangeの未定乗数法が便利です。$(1)-\alpha \times (2) - \beta \times (3)$より

$$-\sum_{i = 1}^{M}(\log{n_{i}}+\alpha+\beta\varepsilon_{i})\delta n_i= 0 \tag{4}$$

各$\delta n_i$は独立だと考えて良いので、
$$\log{n_{i}}+\alpha+\beta\varepsilon_{i} = 0 \quad \Leftrightarrow \quad n_{i} \propto \exp(-\beta\varepsilon_{i}) \tag{5}$$

であり、ボルツマン分布の形が出現します。このように、粒子数、エネルギーによる拘束条件のもと、エントロピーを最大化すると指数関数が登場することがわかりました。人数やチップ数を固定しつつ、チップの授受で系をかき乱し続けたら、これと同じ状況が実現し、指数関数がグラフに現れたのだと理解することができます。

まとめ