森っぽいfunctional graphは直積に関して簡約法則が成り立つ

138

この著者は初心者として投稿しています。間違いや考慮が足りていない点が含まれている可能性が高いです。見つけたらコメント欄で優しく指摘してあげましょう。

まえがき

この記事は [大学数学部門] Mathlog Advent Calendar 2023 のDay 23です.
筆者は基本的に何も知らないので, この記事の内容が含まれる論文や資料, この記事に含まれる一般的でない(好ましくない)定義や言葉遣いなどについてコメント欄で教えてくださるとありがたいです.

動機

ある日僕がふとX(旧Twitter)を眺めると, こんな式が流れてきました.

有限群 $G, H, K$ について, $G \times K ≅ H \times K$ なら $G ≅ H$

そのときの僕はこの式をざっと見ただけで, 参考文献などを確認していなかったので正しいのかどうかもわからなかったんですが, 当時functional graphをいじくっていた僕は一つある考えが浮かびました.

群は集合 $S$ と写像 $f : S \times S \to S$ の組
functional graphは集合 $S$ と写像 $f : S \to S$ の組
つまりfunctional graphでも同じように直積を定義すれば同じ定理が成り立つのでは...!?

ということで, これを証明していきます！
...
...
...
...
...
成り立たねえじゃねえか!!!

反例

$c y c_{n}$ を長さ $n$ の有効閉路とする. またfunctional graphどうしの足し算を非交和で定義し, $n$ 倍を $n$ 個の自分自身の和として定義する( $n = 0$ のときはヌルグラフとする).
また積を, $(G, f) \cdot (H, g) = (G \times H, f \times g)$ とする. ( $f \times g : G \times H \to G \times H$ は $(x, y) \mapsto (f (x), g (y))$ という写像)
このとき,
$c y c_{n} \cdot c y c_{m} = gcd (n, m) c y c_{lcm (n, m)}$
である.
例えば, $3 c y c_{1} \neq c y c_{3}$ だが $3 c y c_{1} \cdot c y c_{3} = 3 c y c_{3} = c y c_{3} \cdot c y c_{3}$

しかしこの例を見てみると, (閉路がすべて自己ループであるfunctional graph)どうしの積は(閉路がすべて自己ループであるfunctional graph)になりそうです.
(閉路がすべて自己ループであるfunctional graph)とは, 自己ループの点を根と見なせば要するに「連結成分がすべて根つき木である森」のことであるので,

functional graphのうち「連結成分がすべて根つき木である森」であるもの全体の集合は直積についてモノイドをなし, 簡約法則が成り立つ

これを証明していきます.

筆者は基本的に何も知らないので, 以降の定義は一般的なものではない可能性が高いです.

基本的な定義

標識 functional graph

集合 $S$ と写像 $f : S \to S$ の組 $(S, f)$ を標識 functional graphと言う.
また $| S |$ を $(S, f)$ の頂点数と言う.
頂点数が有限個の標識 functional graph全体の集合を $G$ とする.

functional graph の同型

functional graph $F = (S, f)$ , $G = (T, g)$ について, 全単射な写像 $h : S \to T$ が存在し
$h \circ f \circ h^{- 1} = g$ が成り立つとき $F$ と $G$ は同型であると言い, $F ≅ G$ と表す.
また $h$ を $F$ から $G$ への同型と言う.

非標識 functional graph

$G / ≅$ の元を非標識 functional graphと言う.
非標識 functional graph 全体の集合を $G$ とする.

functional graph 森, 木

閉路がすべて自己ループである $G$ の元を標識 functional graph 森と言う.
標識 functional graph 森のうち連結であるものを標識 functional graph 木と言う.
非標識のほうも同様に定義する.
非標識 functional graph 森全体の集合を $f$ , 非標識 functional graph 木全体の集合を $t$ とする.

(直)積, (非交)和

$A = (G, f), B = (H, g) \in G$ について,
$A \cdot B = (G \times H, f \times g)$ とする. ( $f \times g : G \times H \to G \times H$ は $(x, y) \mapsto (f (x), g (y))$ という写像)
また $A + B$ を非交和で定義する.

上記の積は $G$ 上で考えてもwell-defindです. またこの積により $G$ は可換モノイドとなり, $f$ と $t$ は $G$ の部分モノイドとなります.

問題

$f$ において簡約法則が成り立つ.

これを示すには $f$ に狭義全順序 $<$ が入ることを示せばよい.

モノイド $M$ に狭義全順序 $<$ が定義され $x < y \Rightarrow a x < a y$ が成り立つとき, 関数 $f (x) = a x$ は単射となる.
よって $a x = a y \Leftrightarrow f (x) = f (y) \Leftrightarrow x = y$

そしてこれを示すには $t$ に狭義全順序 $<$ が入ることを示せばよい.

$t$ において狭義全順序 $<$ が定義され $x < y \Rightarrow a x < a y$ が成り立つとき,
$a, b \in f$ について, $a < b$ を以下のように定義する.

$a$ と $b$ の連結成分の個数を比較したときbのほうが多いなら $a < b$
連結成分の個数が等しいなら, $a, b$ の連結成分を $t$ において定義されている狭義全順序 $<$ で降順にソートし, 辞書順で比較したときに $b$ のほうが大きいなら $a < b$

このときこれは $x < y \Rightarrow a x < a y$ をみたす狭義全順序となる.
$f$ の元は $t$ の元を要素に持つ多重集合ととらえることができる.
一般に, 狭義全順序 $<$ の入った集合 $S$ について, $S$ の元を要素に持つ多重集合全体の集合には上で定義したものと同様の狭義全順序が入り, これを $<_{M}$ ということにする.

$t$ について

$t$ をいい感じの(積と整合性のある)数値の組と同一視したい.
そこで, 自己ループをどうにか処理して普通の有向木に帰着しようと思う.
これを
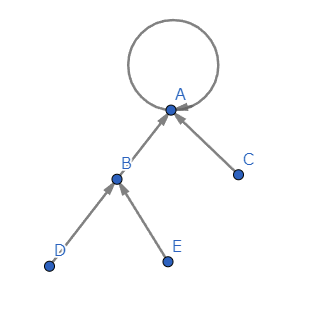functional graph の例
こうして
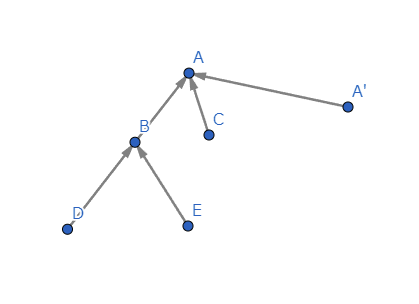自己ループをほどいて...
こうじゃ
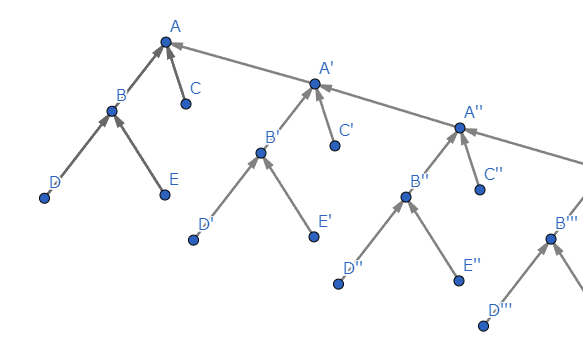無限に続く木に
あとはこの高さ無限の木 $T$ を,
$(T ∖ (深さ 1 以上の頂点), T ∖ (深さ 2 以上の頂点), T ∖ (深さ 3 以上の頂点), \dots)$
という高さ有限の木の列として見ればいい. これを $t$ の元の無限列表示ということにする.
では高さが有限の木はどう表せばいいかと言うと,

非負整数で木を表す

高さ $0, 1$ の木は, 根の入次数を $n$ とすると非負整数 $n$ と同一視できる.
高さ $n - 1$ 以下の木の表し方が定義されているとき, 高さ $n$ 以下の木 $t$ は, $t$ の根の子を $a_{1}, \dots, a_{k}$ とすると
$(t ∖ (深さ n の頂点), {(a_{1} を根とする木), \dots, (a_{n} を根とする木)})$ という, 高さ $n - 1$ 以下の木と, 高さ $n - 1$ 以下の木の多重集合の組として見ることで, 実際の木と一対一の対応のある表し方が定義できる.

そして, 高さ $n - 1$ 以下の木どうしの積が定義されているとき, 高さ $n$ 以下の木どうしの積を

木どうしの積

$S = (s, {s_{1}, \dots, s_{i}}), T = (t, {t_{1}, \dots, t_{i}})$ が高さ $n$ 以下の木のとき,
$S \cdot T = (s \cdot t, {s_{1}, \dots, s_{i}} \cdot {t_{1}, \dots, t_{i}})$
とする. ただし多重集合の積は, 集合同士の積と同じようにそれぞれの元を掛け合わせてできた元全体の集合である(多重集合なので重複も含む).

と定義すると, 「 $t$ の元の積」と, 「 $t$ の元の無限列表示の同じ成分どうしの積」が一致する.

木どうしの狭義全順序

高さ $0, 1$ の木については非負整数と同一視することで狭義全順序 $<$ を定義する.
高さ $n - 1$ 以下の木について狭義全順序 $<$ が定義されているとき, 高さ $n$ 以下の木 $T_{1}, T_{2}$ について, $T_{1} < T_{2}$ を

高さを比べたとき $T_{2}$ の方が高い
高さが同じであれば, $T_{1} = (t_{1}, S_{1})$ , $T_{2} = (t_{2}, S_{2})$ のとき $T_{1} < T_{2} \Leftrightarrow t_{1} < t_{2} または (t_{1} = t_{2} かつ S_{1} <_{M} S_{2})$

と定義する.

$C u t_{n} (x) = (x の深さが n より大きい頂点を全て削除して得られる木)$ とする.

以下の命題は定義より明らかである.

高さ $m (m > n)$ の木 $X, Y$ について $C u t_{n} (X) < C u t_{n} (Y)$ なら $X < Y$

以下の命題の証明は, ちゃんとやろうとするとかなり面倒なので略す.

高さの異なる木の積

高さ $i$ の木 $T_{1}$ と高さ $j > i$ の木 $T_{2}$ について $T_{1} \cdot T_{2} = T_{1} \cdot C u t_{i} (T_{2})$ であり,
特にこれは高さ $i$ の木になる.

$X, Y, A$ の高さが等しいなら $X < Y \Rightarrow A X < A Y$ である

高さが $1$ のときは, 高さが等しい木全体の集合は自然数と同一視できるので明らか.
高さが $n - 1$ のとき成り立つとすると,
高さが $n$ の木 $X = (x, {x_{1}, \dots, x_{i_{1}}}), Y = (y, {y_{1}, \dots, y_{i_{2}}})$ について, $x_{k + 1} \leq x_{k}, y_{k + 1} \leq y_{k}$ としてよく, 明らかに $x, y$ の高さは $n - 1$ で, ${x_{k}}, {y_{k}}$ の中には少なくともひとつ高さが $n - 1$ の元がある.
高さ $n$ の木 $A$ について,
$X < Y$ のとき, $x < y$ なら仮定より明らかに $A X < A Y$ なので $x = y$ , ${x_{k}} < {y_{k}}$ としてよく, $i_{1}, i_{2}$ は $x, y$ によって決まるので $i_{1} = i_{2}$ . また, ${x_{k}}, {y_{k}}$ のうち高さが $n - 1$ 未満の木は, $x, y$ によって決まるので, ${x_{k}}$ と ${y_{k}}$ を比較していったときに一番最初に $x_{t} < y_{t}$ となる $t$ をとってくると, $y_{t}$ の高さは $n - 1$ である必要がある.
$A = (a, {a_{1}, \dots, a_{j}})$ とする. ${a_{k}}$ から高さが $n - 1$ の木だけを取ってくると, $a_{1}, \dots, a_{s}$ となる(これは一個以上存在する).
よって, ${a_{k}} \cdot {x_{k}}$ と ${a_{k}} \cdot {y_{k}}$ を比較するとき, それぞれから $a_{1} y_{t}$ 以上の元のみを抜き出し比較すればよく, 結果 ${a_{k}} \cdot {x_{k}} < {a_{k}} \cdot {y_{k}}$ となる. よって示された.

$X, Y \in t$ について, $X < Y$ を
$X, Y$ の無限列表示が $(X_{0}, X_{1}, \dots), (Y_{0}, Y_{1}, \dots)$ であるとき
$X < Y \Leftrightarrow ある i が存在し X_{i} < Y_{i}$
とすると, $X_{n} = C u t_{n} (X_{m}) (m > n)$ なので命題2よりこれはwell-defindである.
そして命題4により $X, Y, A \in t$ について $X < Y \Rightarrow A X < A Y$ となる.

これが示したいことだった. よって

$f$ において簡約法則が成り立つ.

投稿日：2023年12月22日

更新日：2024年7月8日

この記事を高評価した人

高評価したユーザはいません

この記事に送られたバッジ

バッジはありません。

バッチを贈って投稿者を応援しよう

バッチを贈ると投稿者に現金やAmazonのギフトカードが還元されます。

投稿者

抹茶屋

1905

数弱抹茶より麦茶がすき

他の人のコメント

コメントはありません。

読み込み中

抹茶屋

森っぽいfunctional graphは直積に関して簡約法則が成り立つ

まえがき
動機
基本的な定義
問題
$\mathbb{t}$について

森っぽいfunctional graphは直積に関して簡約法則が成り立つ

まえがき

動機

基本的な定義

問題

𝕥tについて

この記事を高評価した人

この記事に送られたバッジ

投稿者

コメント

他の人のコメント

$t$ について