特性サイクルと柏原の指数定理
この節では構成可能層の特性サイクルと柏原の指数定理について説明したいと思います.特性サイクルは大雑把にはマイクロ台に重複度の概念を加えたもので,マイクロ台よりも多くの情報を持つと考えられます.実際,構成可能層のオイラー・ポアンカレ標数が特性サイクルを使って計算できるというのが柏原の指数定理です.この指数定理はポアンカレ・ホップの定理の構成可能層係数への拡張とみなすことができます.
特性サイクル
構成可能層の特性サイクルはマイクロ台に重複度の情報を付け足したものと見ることができます.以下それを天下り的に定義して性質を見ていきましょう.
$F \in \DbRc(X)$とすると, 第6節 の定理2より$\MS(F)$は$T^*X$の劣解析的ラグランジュ錐状閉部分集合となります.ゆえに,ある$\MS(F)$の開稠密部分集合$\Lambda_0$が存在して次を満たします:
連結成分への分解$\Lambda_0=\bigsqcup_{i \in I} \Lambda_i$を考えると,任意の$i \in I$に対して$X$の部分多様体$X_i$であって$\Lambda_i \subset T^*_{X_i}X$を満たすものが存在する.
すると,各$i \in I$に対して$p \in \Lambda_i$を取れば$p$の近傍で$\MS(F) \subset T^*_{X_i}X$なので,
第3節
の命題3より$V \in \Db(\bfk)$が存在して,$\Db(\bfk_X;p)$において$F \simeq V_{X_i}$を満たします.これは前節(
第7節
)でも使った議論でしたね.実はこの$V$は$p$の取り方によらず連結な$\Lambda_i$上一定であることを示すことができるので,$\Lambda_i$に固有なものと考えることができます.しかも,$V$は
第3節
でも見たように$F$から具体的に計算することもできます.実際,$x_0=\pi(x) \in X_i$として$x_0$の近傍で定義された$C^\omega$級函数$\varphi \colon X \to \bbR$で2条件
(1) $p=(x_0;d\varphi(x_0))$,
(2) $\varphi|_{X_i}$は$x_0$の近傍でモース函数であり,$x_0$におけるモース指数は$0$
を満たすものを取れば
$$
V \simeq \RG_{\{ \varphi \ge \varphi(x_0) \}}(F)_{x_0}
$$
が成り立ちます.特に,$F \in \DbRc(\bfk_X)$より$V \in \Db(\bfk)$の全てのコホモロジーは有限次元になることが分かります.そこで$V$のオイラー・ポアンカレ標数 (Euler-Poincaré characteristic)
$$
\chi(V) := \sum_{n \in \bbZ} (-1)^n \dim H^n(V)
$$
を用いて,$\Lambda_i$上での$F$の重みを$m_i(F):=\chi(V)$と定めます.
上で見たように各$\Lambda_i$に対して$F$による重み$m_i(F)$が定まったので,この重みを乗せた$\Lambda_i$の形式和を考えたくなり,この形式和は$T^*X$内の向き付けられた劣解析的ラグランジュ部分集合によるチェインを定めます.実際,$T^*_{X_i}X$には標準的な向き付けが入るので,$[\Lambda_i]$という記号で$\Lambda_i$上では$[T^*_{X_i}X]$である$\overline{\Lambda_i}$に台を持つチェインをあらわすと,重み付き形式和は
$$
\sum_{i \in I} m_i(F) [\Lambda_i]
$$
となります.このチェインが適切な意味でサイクルになっているというのが柏原によって証明されたことです.
$F \in \DbRc(X)$とする.$\Lambda_0=\bigsqcup_{i \in I}\Lambda_i \subset \MS(F)$と$m_i(F) \in \bbZ$を上のように定める.このとき,$T^*X$上の(劣解析的錐状)ラグランジュサイクル$CC(F)$を
$$
CC(F):= \sum_{i \in I} m_i(F) [\Lambda_i]
$$
と定めて,$F$の特性サイクル (characteristic cycle) と呼ぶ.
簡単な場合に特性サイクルがどうなるかいくつか例を見る.
(i) $F=\bfk_X$なる定数層のとき,$CC(F)=[0_X]$である.
(ii) より一般に,コホモロジーの次元が有限な$V \in \Db(\bfk)$と$X$の部分多様体$M$に対して$F=V_M$であるときを考える.このとき,
$$
CC(F)=\left( \sum_{n \in \bbZ} (-1)^n \dim H^n(V) \right) [T^*_MX]
$$
である.特に,$CC(\bfk_M)=[T^*_MX]$である.
(iii) $X=\bbR$として$(t;\tau)$を$T^*\bbR$の斉次座標とする.この状況で閉区間上の定数層のゼロ拡張$F=\bfk_{[0,1]}$の特性サイクルがどうなるか見る.マイクロ台の計算は
第1節
の例4を参照せよ.このとき,$p_0=(0;1)$での超局所圏$\Db(\bfk_\bbR;p_0)$において$F \simeq \bfk_{\{0\}}$であり$p_1=(1;-1)$での超局所圏$\Db(\bfk_\bbR;p_1)$においても$F \simeq \bfk_{\{1\}}$となる.したがって,
$$
CC(F)
= ([T^*_0\bbR] \cap \{ \tau >0 \})
+ ([0_\bbR] \cap \{ 0< t<1 \})
+ ([T^*_1\bbR] \cap \{ \tau<0 \})
$$
となる.図で表示すると以下の図1のようになる.
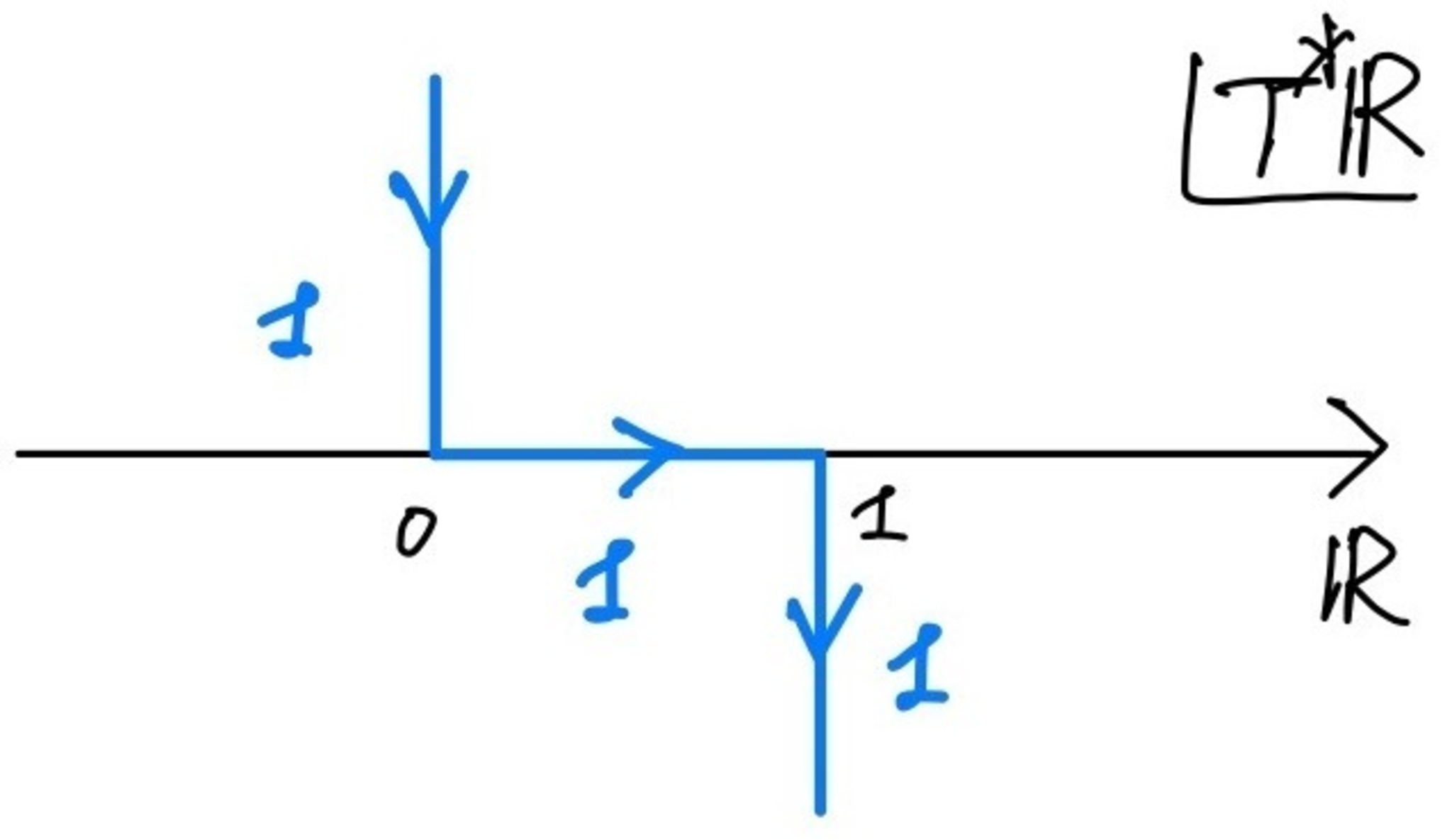 閉区間上の定数層のゼロ拡張の特性サイクル
閉区間上の定数層のゼロ拡張の特性サイクル
(iv) 上と同じ状況で,今度は半開区間上の定数層のゼロ拡張$F=\bfk_{[0,1)]}$の特性サイクルを考える.上と同様にマイクロ台の計算は
第1節
の例4を参照.このときは,$p'_1=(1;1)$での超局所圏$\Db(\bfk_\bbR;p'_1)$においては$F \simeq \bfk_{\{1\}}[-1]$となる(例えば完全三角$\bfk_{[0,1)} \to \bfk_{[0,1]} \to \bfk_{\{1\}} \to \bfk_{[0,1)}[1]$を考えれば分かる).したがって,この場合は
$$
CC(F)
= ([T^*_0\bbR] \cap \{ \tau >0 \})
+ ([0_\bbR] \cap \{ 0< t<1 \})
- ([T^*_1\bbR] \cap \{ \tau>0 \})
$$
となる.図で表示すると以下の図2のようになる.ここでマイナス符号は向きを反対にすることであらわした.
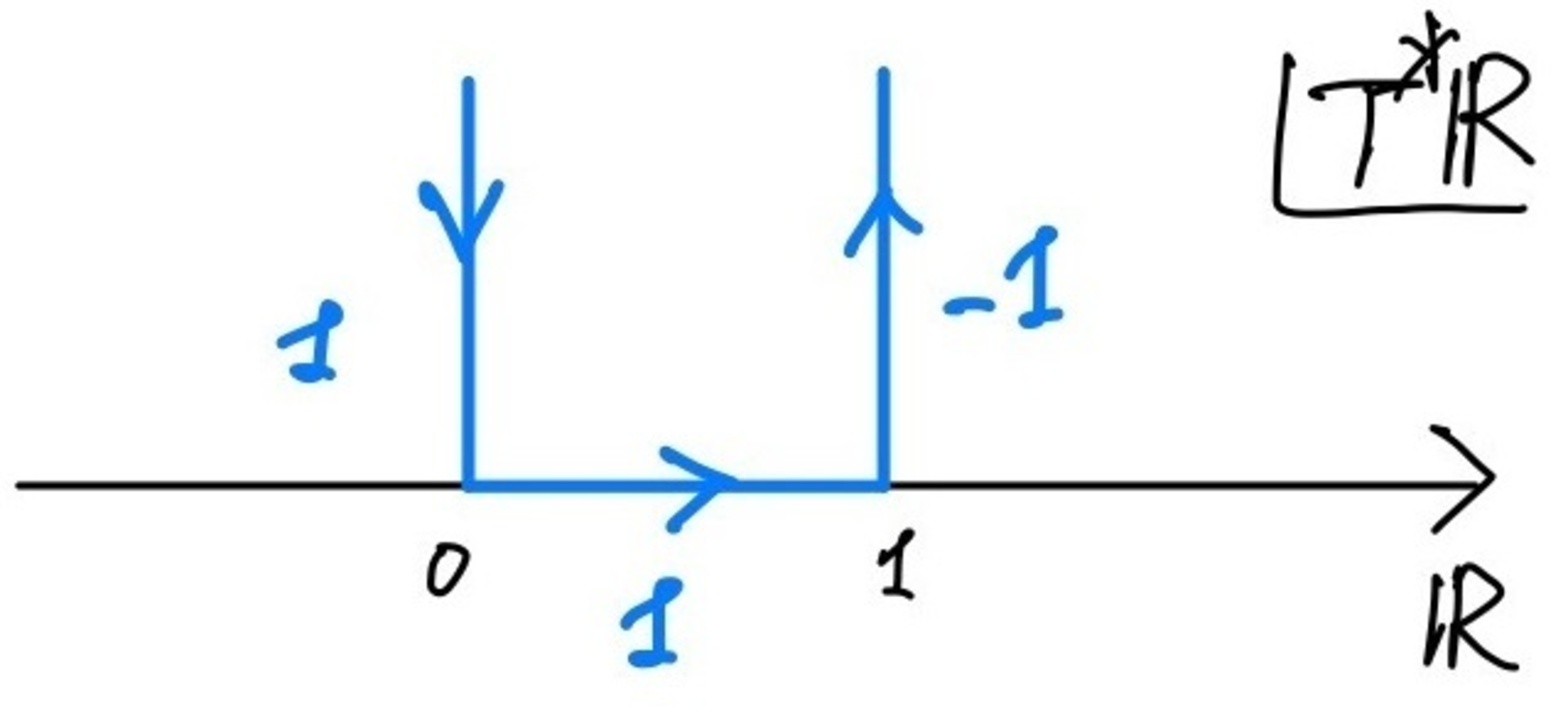 半開区間上の定数層のゼロ拡張の特性サイクル
半開区間上の定数層のゼロ拡張の特性サイクル
定義からすぐ分かる特性サイクルの性質を述べておきます.
(i) $F \in \DbRc(\bfk_X)$と$k \in \bbZ$に対して,
$$
CC(F[k]) = (-1)^k CC(F)
$$
が成り立つ.
(ii) $\DbRc(\bfk_X)$における完全三角$F \to G \to H \to F[1]$に対して,
$$
CC(G) = CC(F) + CC(H)
$$
が成り立つ.
(i)は$\chi(V[k])=(-1)^k \chi(V)$であることから,(ii)は$\Lambda_0=\bigsqcup_{i} \Lambda_i$が共通に取れて$m_i(G)=m_i(F)+m_i(H)$となることから従う.(i)は(ii)で$G=0$の場合を考えることでも示せる.
柏原の指数定理
上で天下り的に定義した特性サイクルは超局所的なオイラー・ポアンカレ標数を重みにして定義されていました.一方で,$F \in \DbRc(\bfk_X)$の台$\Supp(F)$がコンパクトならば,
第6節
の命題4(i)より$a_X \colon X \to \pt$を一点への写像として
$$
\RG(X;F) \simeq R{a_X}_*F \in \DbRc(\bfk_\pt)
$$
となります.これはつまり任意の$n \in \bbZ$に対して$\RG(X;F)$のコホモロジー$H^n(X;F)=H^n \RG(X;F)$が有限次元となることを示しているので,$F$の$X$上のオイラー・ポアンカレ標数
$$
\chi(X;F) := \chi(\RG(X;F)) = \sum_{n \in \bbZ} (-1)^n \dim H^n(X;F)
$$
がwell-definedになります.すると,この大域的なオイラー・ポアンカレ標数を超局所的な対象である特性サイクル$CC(F)$から計算できるかという問いが浮かんできます.これがYesだというのが柏原の(超局所的)指数定理なのです.
指数定理を述べるために記号を少し準備します.$\sigma \colon X \to T^*X$を$\pi \colon T^*X \to X$の連続な切断とすると,それに付随する$T^*X$上のサイクル$[\sigma]$が定まります(劣解析的ではないのでここではごまかしていますが後でもう少し詳しく説明します).$X$の向き付けから自然に$\sigma(X)$に向き付けが入ることにも注意しましょう.例えば$\varphi \colon X \to \bbR$を$C^\infty$級函数とすると,$\sigma_\varphi \colon x \mapsto (x;d\varphi(x))$は$\pi$の切断なので,$T^*X$上のサイクル$[\sigma_\varphi]$を定めます.$\lambda$を$T^*X$上のラグランジュサイクルと連続切断$\sigma \colon X \to T^*X$に対して$\sigma(X) \cap \supp(\lambda)$がコンパクトならば,それらの交点数 (intersection number)
$$
\#([\sigma] \cap \lambda) \in \bbZ
$$
が定まります.交点数の符号は書物によって異なる気がしますが,Sheaves on Manifoldsに合わせて以下の例のようになるように約束します.
交叉が横断的ないくつかの場合に交点数の例を見る.
(i) $X=\bbR$の場合に$T^*\bbR$上のサイクル$[T^*_0\bbR]$を考える.$\sigma \colon X \to T^*X$を$C^\infty$級の切断として$\sigma(\bbR)$が$T^*_0\bbR$と図3のように横断的に交わるとする.このとき,$\#([\sigma] \cap [T^*_0\bbR])=+1$である.
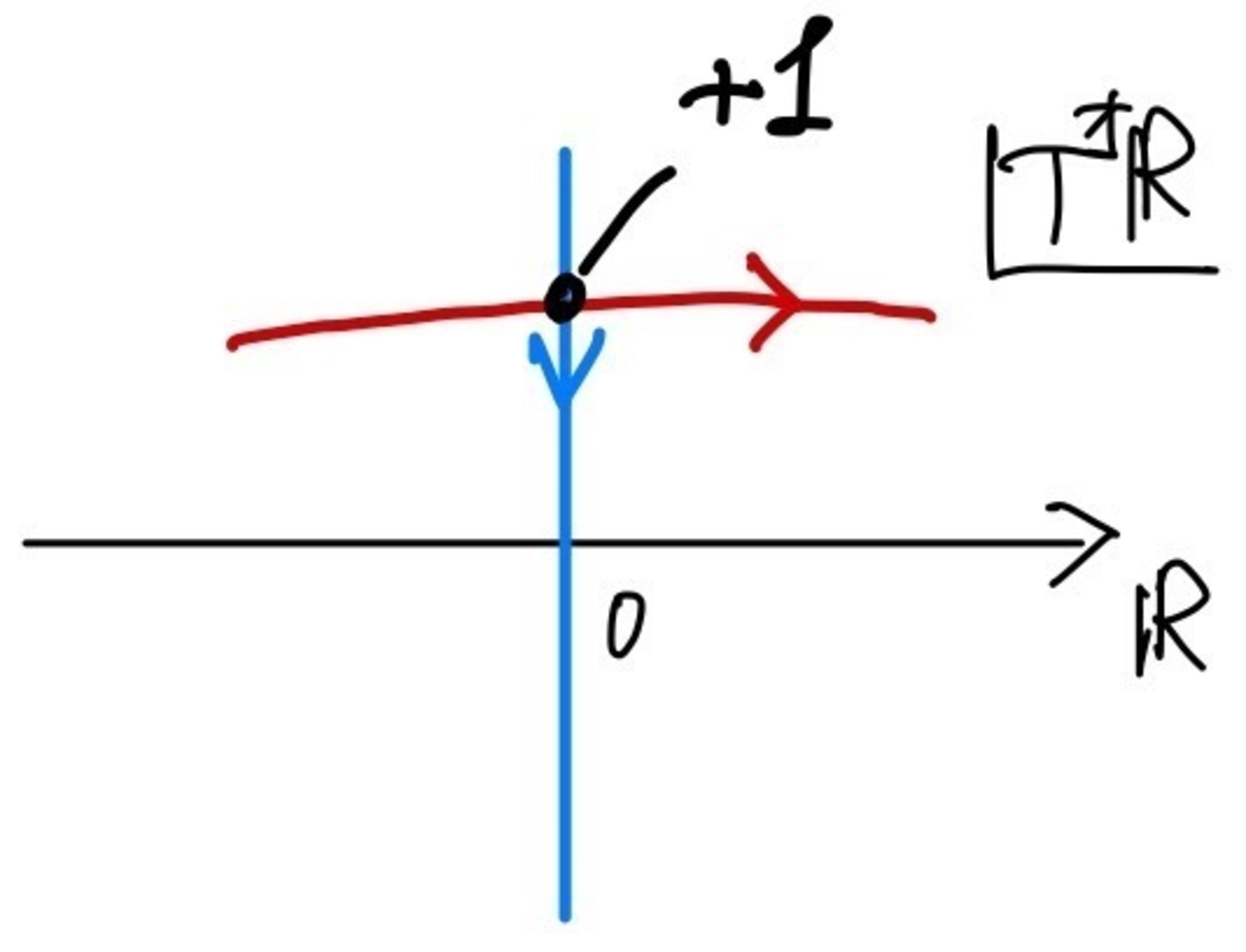 切断とファイバーサイクルの交点数
切断とファイバーサイクルの交点数
(ii) 再び$X=\bbR$の状況で$[0_X]$というサイクルを考える.このとき,ゼロ切断に横断的な切断$\sigma \colon X \to T^*X$について交点数$\#([\sigma] \cap [0_X])$は図4のようになる.
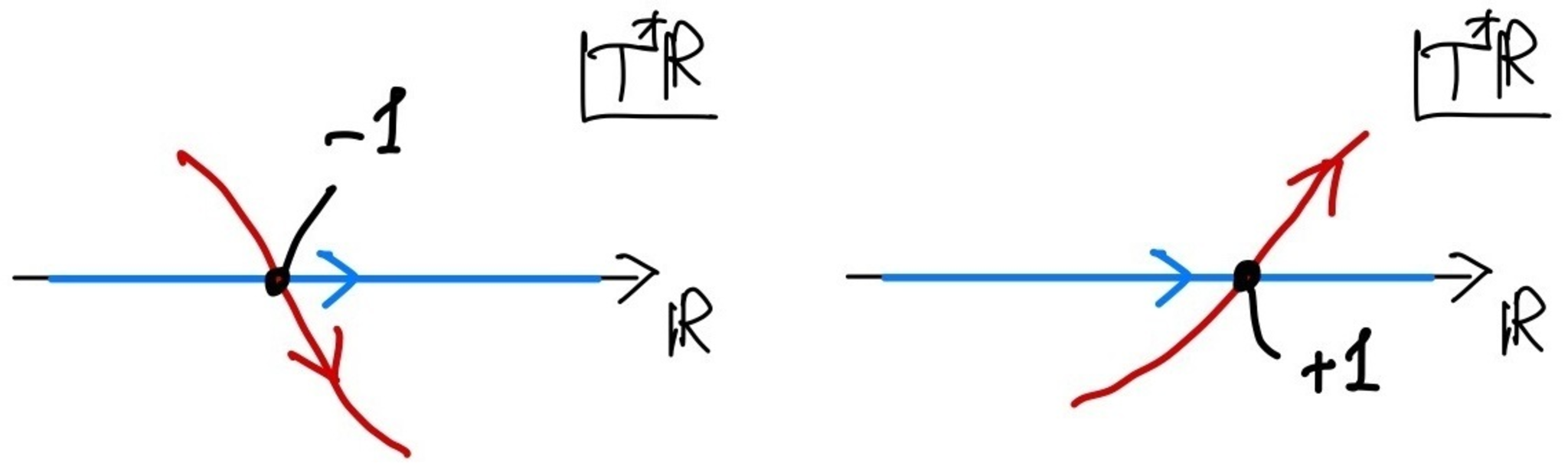 切断とゼロ切断サイクルとの交点数
切断とゼロ切断サイクルとの交点数
(iii) $v$を$X$上のベクトル場,すなわち接束の切断$v \colon X \to TX$とする.$X$にリーマン計量を与えて$TX$と$T^*X$を同一視すれば,$v$は余接束の切断$\sigma_v \colon X \to T^*X$とみなせる.$v$は孤立した零点のみを持つと仮定すると,$[\sigma_v]$と$[0_X]$との交点数の零点$x_0$における寄与は
$$
\#_{x_0} ([\sigma_v] \cap [0_X]) = \ind(x_0;v)
$$
と$v$の$x_0$における指数と一致する.
(iv) 上と同様に,$\varphi \colon X \to \bbR$を$C^\infty$級函数として$\sigma_\varphi \colon X \to T^*X, x \mapsto (x;d\varphi(x))$という切断を考える.$\sigma_\varphi(X) \cap 0_X$は$\varphi$の臨界点に対応する.$\varphi$がモース函数であると仮定すると,$[\sigma_\varphi]$と$[0_X]$との交点数の臨界点$x_0$における寄与は
$$
\#_{x_0} ([\sigma_v] \cap [0_X]) = (-1)^{\ind(x_0;\varphi)}
$$
とモース指数$\ind(x_0;\varphi)$の分の符号と一致する.
上で見た交点数の概念を使うと柏原の指数定理を次のように述べることができます.
$F \in \DbRc(\bfk_X)$として$\Supp(F)$がコンパクトであると仮定する.$\sigma \colon X \to T^*X$を連続な切断とする.このとき,等式
$$
\chi(X;F)=\#([\sigma] \cap CC(F))
$$
が成り立つ.
定理の主張でうれしいことは,任意の連続切断$\sigma \colon X \to T^*X$に対して$F$のオイラー・ポアンカレ標数が交点数で計算できることです.計算しやすいように$\sigma$をうまくとってやることで簡単に左辺が計算できる場合があります.勝手な連続切断との超局所的な交点数で大域的な不変量が計算できるのが面白いところです.
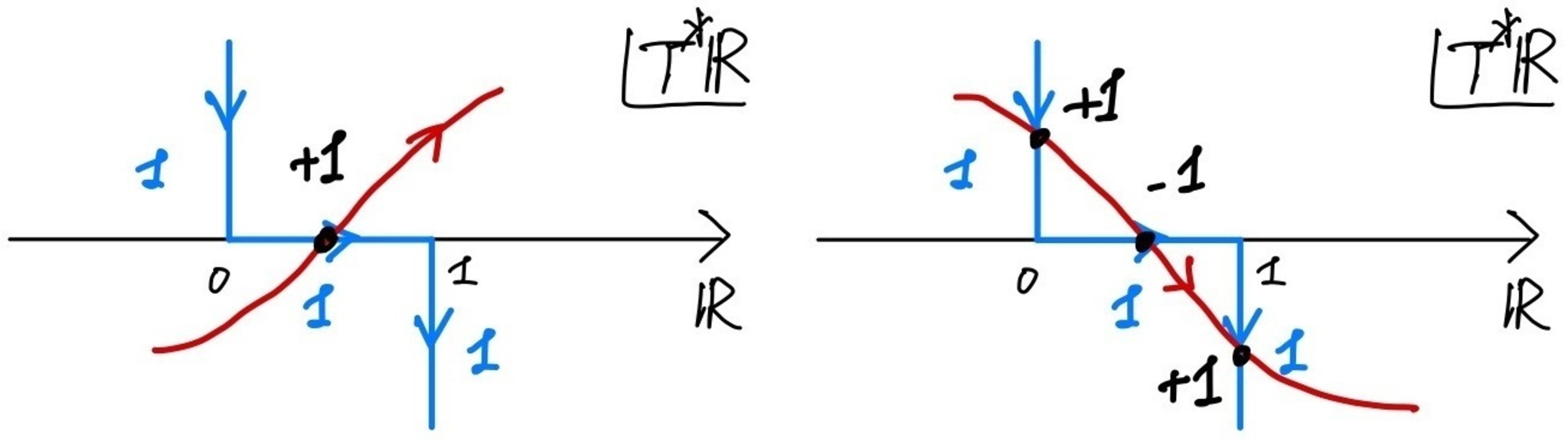
(i) $X=\bbR$として,上の例1の(iii)で見た閉区間上の定数層のゼロ拡張$\bfk_{[0,1]}$について考える.切断$\sigma \colon X \to T^*\bbR$の取り方によって,以下の図5のように交点数が計算できる.いずれの場合も局所寄与の和は$1$であり,$\chi(\bbR;\bfk_{[0,1]})=\dim H^0(\bbR;\bfk_{[0,1]})=1$に一致していることが分かる.
 閉区間上の定数層のゼロ拡張の指数定理
閉区間上の定数層のゼロ拡張の指数定理
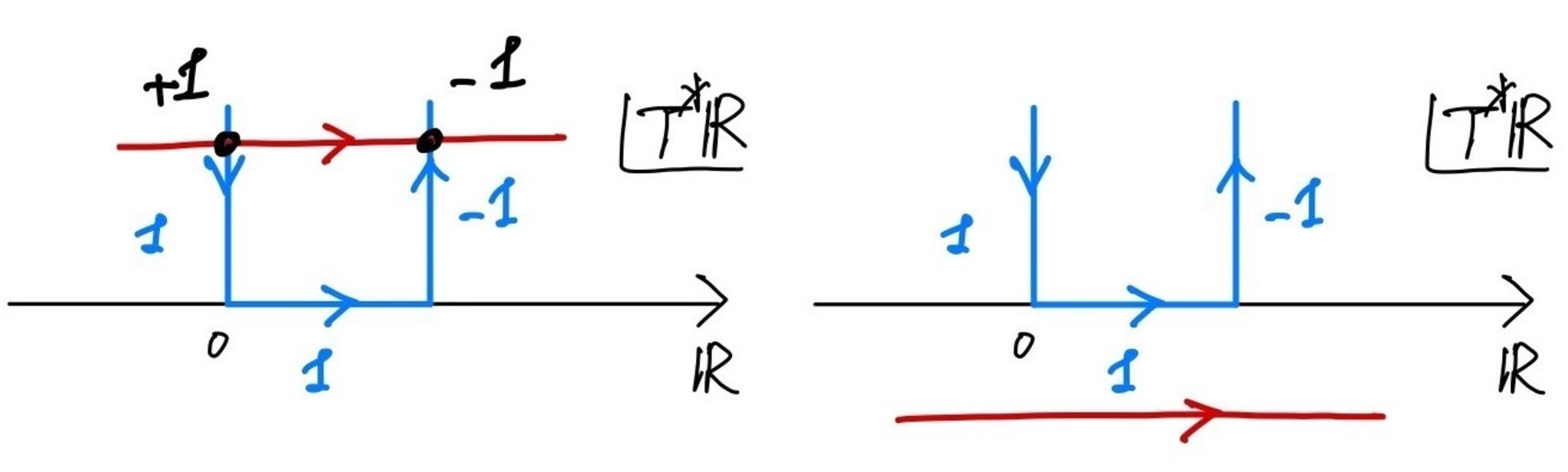
(ii) 今度は$X=\bbR$として,上の例1の(iv)で見た半開区間上の定数層のゼロ拡張$\bfk_{[0,1)}$について考える.切断の取り方によって,交点数は以下の図6のように計算され,その局所寄与の和はいずれの場合も$0$である.これは$\chi(\bbR;\bfk_{[0,1)})=0$に一致している.
 半開区間上の定数層のゼロ拡張の指数定理
半開区間上の定数層のゼロ拡張の指数定理
(iii) $X$がコンパクトであると仮定する.$CC(\bfk_X)=[0_X]$であったことを思い出そう.上の例2の(iii)で見たように$X$上の孤立零点のみを持つベクトル場$v$をリーマン計量を通して$T^*X$の切断$\sigma_v$とみなした際には,柏原の指数定理を定数層$\bfk_X$に用いることによって
$$
\chi(X) = \chi(X;\bfk_X) = \#([\sigma_v] \cap [0_X]) = \sum_{x} \ind(x;v)
$$
が得られる.ここで$x$は全ての零点をわたる.これはポアンカレ・ホップの定理である.同様に例2の(iv)で見たことから,$\varphi \colon X \to \bbR$をモース函数とすると,
$$
\chi(X) = \chi(X;\bfk_X) = \#([\sigma_\varphi] \cap [0_X]) = \sum_{x} (-1)^{\ind(x;v)}
$$
が得られる.ここで$x$は全ての$\varphi$の臨界点をわたる.
$\mu hom$からの特性サイクルと演算に対する自然性
ここではSheaves on Manifoldsで説明されている$\mu hom$を通した特性サイクルの構成について説明します.ここは結構技術的なので,興味がない人は読み飛ばして次の小節に行ってください.
今度は指数定理を念頭において,まずBorel-Mooreホモロジー類で構成可能層のオイラー・ポアンカレ標数を計算できるものを考えてみましょう.$F \in \DbRc(\bfk_X)$として,Verdier双対$D_X F=\cRHom(F,\omega_X)$を考えます.すると,定義からトレース射$\tr \colon F \otimes D_X F \to \omega_X$が存在します.有限次元ベクトル空間$V$に対して$\Hom(V,V) \simeq V \otimes V^\vee \to \bfk$の$\id_V$の像が$V$の次元になるので,これを$X$が一点の場合と思って構成可能層で類似を考えてみます.すると,
第6節
の命題1で見た同形と上付きびっくりの性質(
層理論と導来圏第8節
の命題6)から,$\delta \colon X \to X \times X$を対角射として,$\DbRc(\bfk_X)$における同形
$$
\delta^! (F \boxtimes D_XF) \simeq \delta^! \cRHom(q_2^{-1}F,q_1^!F) \simeq \cRHom(F,F)
$$
が得られます.$\Delta=\delta(X)$とすると$\delta^! \simeq \delta^{-1} \RG_{\Delta}$なので射$\delta^! \to \delta^{-1}$が存在します.これによって,次の射の列が得られます:
\begin{align}
\cRHom(F,F)
& \simeq \delta^! (F \boxtimes D_X F) \\
& \to \delta^{-1} (F \boxtimes D_X F) \\
& \simeq F \otimes D_X F \\
& \underset{\tr}{\to} \omega_X.
\end{align}
大域切断を取って得られる射による$\id_F \in \Hom(F,F)$の像を$C(F) \in H^0_{\Supp(F)}(X;\omega_X)$と書いて,しばしば$F$の特性類(または$F$のオイラー類)と呼んだりします.真面目に考えると作り方から
$$
\chi(X;F) = \int_X C(F)
$$
が成り立つことが分かります.
さて,上の構成を$\mu hom$を使って余接束$T^*X$に持ち上げることを考えてみましょう.$\mu hom$の性質は
第5節
を見てください.同形$R\pi_* \mu hom(F,F) \simeq \cRHom(F,F)$と随伴による射$\id \to \delta_* \delta^{-1}$を用いると,次の射の列が得られます:
\begin{align}
\cRHom(F,F)
& \simeq R \pi_* \mu hom(F,F) \\
& \simeq R \pi_* \RG_{\MS(F)} \mu hom(F,F) \\
& \simeq R \pi_* \RG_{\MS(F)} \mu_\Delta (F \boxtimes D_X F) \\
& \to R \pi_* \RG_{\MS(F)} \mu_\Delta (\delta_* (F \otimes D_X F)) \\
& \underset{\tr}{\to} R \pi_* \RG_{\MS(F)} \mu_\Delta (\delta_* \omega_X) \\
& \simeq R \pi_* \RG_{\MS(F)} (\pi^{-1}\omega_X).
\end{align}
ここで二つ目の同形は$\Supp(\mu hom(F,F)) = \MS(F)$から,三つ目の同形は$\mu hom$の定義と
第6節
の命題1の同形から従います.最後の同形は説明していない超局所化の演算に対する自然性からチェックすることができます.大域切断を取ると射$\Hom(F,F) \to H^0_{\MS(F)}(T^*X;\pi^{-1}\omega_X)$が得られます.
上の射による$\id_F \in \Hom(F,F)$の像を$CC(F) \in H^0_{\MS(F)}(T^*X;\pi^{-1}\omega_X)$と書き,$F$の特性サイクル(または$F$の超局所オイラー類 (microlocal Euler class))と呼ぶ.
このように見ると構成可能層の特性類を余接束に持ち上げたのだから指数定理が成り立ちそうな気がしてきませんか?実際,指数定理の主張をもう少し真面目に見ると以下のようになります.$\sigma \colon X \to T^*X$を連続切断とすると上付きびっくりの随伴から,同形
\begin{align}
H^0_{\sigma(X)}(T^*X;\pi^!\bfk_X)
& \simeq \Hom(\sigma_! \bfk_X, \pi^!\bfk_X) \\
& \simeq \Hom(\bfk_X, \sigma^! \pi^! \bfk_X) \simeq H^0(X;\bfk_X)
\end{align}
が成り立ちます.この同形による$1 \in H^0(X;\bfk_X)$の像が上で書いた$[\sigma] \in H^0_{\sigma(X)}(T^*X;\pi^!\bfk_X)$の正確な意味です.上付きびっくりの射(
層理論と導来圏第8節
の命題8)により射$\pi^! \bfk_X \otimes \pi^{-1} \omega_X \to \pi^! \omega_X \simeq \omega_{T^*X}$が得られるので,テンソル積により$\lambda \in H^0(T^*X;\pi^{-1}\omega_X)$に対して
$$
[\sigma] \cap \lambda \in H^0_{\sigma(X) \cap \supp(\lambda)}(T^*X;\omega_{T^*X})
$$
が定まります.$\sigma(X) \cap \supp(\lambda)$がコンパクトなら積分できて,それが交点数$\#([\sigma] \cap \lambda)$です.$T^*X$の閉部分集合$S$で$\pi$がその上で固有となるものに対して,射$\alpha \colon H^0_S(T^*X;\omega_{T^*X}) \to H^0_S(X;\omega_X)$が定まります.構成から,この射について
$$
\alpha([\sigma] \cap CC(F)) = C(F)
$$
となることがチェックできるので,$\chi(X;F)=\int_X C(F)$と合わせて柏原の指数定理が得られるという仕組みになっています.
上で見た形式和としてのサイクルによる表示との関係を少しだけ述べておきます.実は,$\Lambda$が劣解析的錐状閉isotropicな部分集合をわたる際の帰納極限$\cL_X=\varinjlim_{\Lambda} H^0_\Lambda(\pi^{-1}\omega_X)$を考えると,これは$T^*X$上のラグランジュサイクルの層になることがチェックできます.したがって,
$$
CC(F) \in H^0_{\MS(F)}(T^*X;\pi^{-1}\omega_X) \subset H^0(T^*X;\cL_X)
$$
と特性サイクルはラグランジュサイクルとみなせるのです.
この$\mu hom$を使った構成は,演算に対する自然性を得るのに見通しが良いという利点があります.すなわち,多様体の射$f \colon X \to Y$に対する適当な条件の下で射
\begin{align}
& f_* \colon H^0_{\Lambda_X}(T^*X;\pi_X^{-1}\omega_X) \to H^0_{f_\pi f_d^{-1}(\Lambda_X)}(T^*Y;\pi_Y^{-1}\omega_Y) \\
& f^* \colon H^0_{\Lambda_Y}(T^*Y;\pi_Y^{-1}\omega_Y) \to H^0_{f_d f_\pi^{-1}(\Lambda_Y)}(T^*X;\pi_X^{-1}\omega_X)
\end{align}
が定まります.上の$\mu hom$による構成に$Rf_*, f^{-1}$を施して大きな可換図式を真面目に追いかけることによって次が証明できます.
$f \colon X \to Y$を多様体の射とする.
(i) $F \in \DbRc(\bfk_X)$として$f$が$\Supp(F)$上固有であると仮定する.このとき,等式
$$
CC(Rf_*F) = f_* CC(F)
$$
が成り立つ.
(ii) $G \in \DbRc(\bfk_Y)$として$f$が$F$に対して非特性的であると仮定する.このとき,等式
$$
CC(f^{-1}G) = f^*CC(G)
$$
が成り立つ.
近年ではさらに広く核の層に対して超局所オイラー類を対応させて,その広い枠組みの中で自然性を示すという研究も行われています.
ラグランジュサイクルと構成可能函数
実は,構成可能層の特性サイクルは構成可能函数というものと密接に関わっているので,ここでほんの少しだけ説明します.構成可能層は$\mu$-stratification $X=\bigsqcup_{\alpha \in A}X_\alpha$が存在して,各$X_\alpha$上コホモロジー層が局所定数層となるものとして定義されました.構成可能函数はこの函数版です.
函数$\varphi \colon X \to \bbZ$が$X$上の($\bbZ$値の)構成可能函数であるとは,$X$の$\mu$-stratification $X=\bigsqcup_{\alpha \in A}X_\alpha$が存在して,各$\alpha$に対して$\varphi|_{X_\alpha}$が定数函数になることをいう.$\CF(X)$で$X$上の構成可能函数の集合をあらわす.
$F \in \DbRc(\bfk_X)$と$x \in X$に対して
$$
\chi(F)(x) := \chi(F_x) = \sum_{n \in \bbZ} (-1)^n \dim H^n(F_x)
$$
と定めると,$\chi(F)$は$X$上の構成可能函数である.
構成可能函数に関しては,次のように引き戻し・積分・押し出しが定まります:
- (引き戻し)$f \colon X \to Y$を多様体の射とするとき,$\psi \in \CF(Y)$に対して
$$ (f^*\psi)(x) = \psi(f(x)) $$
と定めると,$f^*\psi \in \CF(X)$となる. - (積分)$\varphi \in \CF(X)$として$\supp(\varphi)$がコンパクトであると仮定する.このとき,$X$のある$\mu$-stratification $X=\bigsqcup_{\alpha \in A}X_\alpha$で各$X_\alpha$が相対コンパクトであるものを取って$\varphi=\sum_{\alpha \in A} c_\alpha \mathbf{1}_{X_\alpha}$とあらわされる.ここで$\mathbf{1}_Z$は$Z$の特性函数である.この表示のもとで
\begin{align} \int_X \varphi d\chi & := \sum_{\alpha \in A} c_\alpha \chi(X;\bfk_{X_\alpha}) \\ & = \sum_{\alpha \in A} c_\alpha \chi_c(X_\alpha) \end{align}
と定める.ここで$\chi_c(X_\alpha)=\sum_{n \in \bbZ} (-1)^n \dim H^n_c(X_\alpha;\bfk_{X_\alpha})$は$X_\alpha$のコンパクト台オイラー・ポアンカレ標数である.この積分は,コンパクト台オイラー・ポアンカレ標数を有限加法的な測度とみなして積分したものとも思える. - (押し出し)$f \colon X \to Y$を多様体の射とするとき,$\varphi$に対して
$$ (f_*\varphi)(y) := \int_{X} \varphi \cdot \mathbf{1}_{f^{-1}(y)} d\chi $$
と定めると,$f_* \varphi \in \CF(Y)$となる.
次に構成可能層との関連を説明しましょう.上の例4で見た構成可能層に対する茎ごとのオイラー・ポアンカレ標数は写像$\chi \colon \Ob(\DbRc(\bfk_X)) \to \CF(X)$を定めていて,完全三角$F \to G \to H \to F[1]$に対して
$$
\chi(G) = \chi(F) +\chi(H)
$$
が成り立つことが分かります.$\KRc(X)$を$\DbRc(\bfk_X)$のGrothendieck群とすると,アーベル群の射
$$
\chi \colon \KRc(X) \to \CF(X)
$$
が誘導されます.ここで$\KRc(X)$は,$\Ob(\DbRc(\bfk_X))$の対象で生成された自由アーベル群を完全三角$F \to G \to H \to F[1]$が存在するときに$G=F+H$の関係で割ったアーベル群のことでした.実はこの対応は同形
$$
\chi \colon \KRc(X) \simto \CF(X)
$$
を引き起こし,この同形を通して構成可能層の逆像・順像と構成可能函数の引き戻し・押し出しが対応します.すなわち,多様体の射$f \colon X \to Y$,$F \in \DbRc(\bfk_X)$であって$\Supp(F)$上$f$が固有となるものと$G \in \DbRc(\bfk_Y)$に対して
\begin{align}
f^* \chi(G) & = \chi(f^{-1}G) \\
f_* \chi(F) & = \chi(Rf_*G)
\end{align}
が成り立ちます.実はVerdier双対に対応する構成可能函数側の操作も考えられますが,ここでは詳しく述べません.
最後にラグランジュサイクルとの関わりを説明します.$\cL_X$で$T^*X$上のラグランジュサイクルの層をあらわします.すると,上の命題1の(ii)より特性サイクルを対応させる写像は群の射
$$
CC \colon \KRc(X) \to H^0(T^*X;\cL_X)
$$
を誘導します.実はこの群の射は同形になります.全射であることはラグランジュサイクル$\lambda$に対して$\pi(\supp(\lambda))$に関する帰納法で示せます.単射であることはだいたい次のようにして示せます.
$F \in \DbRc(\bfk_X)$として$CC(F)=0$ならば$F \simeq 0$を示せばよい.同形$\chi \colon \KRc(X) \simto \CF(X)$から任意の$x \in X$に対して$\chi(F)(x)=0$であることをいえばよい.$x_0 \in X$を固定して,$x_0$の近傍で定義された$C^\omega$級函数$\varphi \colon X \to \bbR$で$\varphi(x_0)=0, d\varphi(x_0)=0$かつ$x_0$における$\varphi$のヘシアンが正定値となるものを取る.すると,サード型の定理から$x_0$は$\MS(F) \cap \sigma_\varphi(X)$の孤立点になる.したがって,$x_0$の近傍で指数定理を用いると
$$
\chi(F)(x_0) = \#([\sigma_\varphi] \cap CC(F))
$$
が得られる(コンパクト性についてごまかしたので上の指数定理の主張からは従わないが正当化できる).今$CC(F)=0$なので左辺も$0$である.
これまでに見た構成可能層のGrothendieck群・構成可能函数のなすアーベル群・ラグランジュサイクルのなすアーベル群の三つが同形であるという主張を述べておきましょう.
あるアーベル群の射$\Eu \colon H^0(T^*X;\cL_X) \to \CF(X)$が存在して,図式
$$
\xymatrix{
& \KRc(X) \ar[ld]_-{CC} \ar[rd]^-{\chi} & \\
H^0(T^*X;\cL_X) \ar[rr]_-{\Eu} & & \CF(X)
}
$$
が可換で全ての射が同形となるものが存在する.さらに,これらの同形はそれぞれの演算と両立する.
$\Eu$はオイラー写像と呼ばれることがあり,特異点論で現れるオイラー障害 (Euler obstruction) とも深い関わりがあります.詳しくは参考文献に挙げた本を参照してください.
まとめ
この節では
- 重み付き形式和としての特性サイクル
- 柏原の超局所的指数定理
- $\mu hom$を用いた特性サイクルの構成法と自然性
- 構成可能層・ラグランジュサイクル・構成可能函数の関係
について説明しました.
参考文献
この本を高評価した人
この本に送られたバッジ
投稿者
コメント
他の人のコメント

