複素数平面

高校数学

複素数平面

複素数平面ってなに？

複素数は実数も含むし、純虚数も含むよ！

複素数をすべてを平面上の座標であらわしたもの！

$a+bi$を$(x,y)=(a,b)$に対応させる！

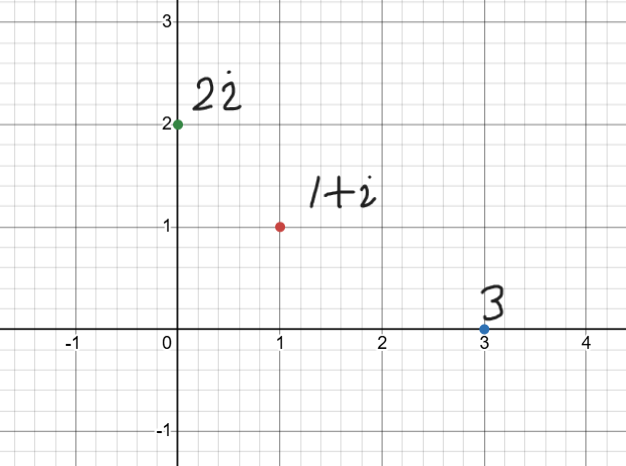
例えば...

$1+i$は$(1,1)$
$3$は$(3,0)$
$2i$は$(0,2)$って感じだね

$(1+i)^n$の秘密

$(1+i)^n$の小さな$n$について値を調べてみよう

$(1+i)^1=1+i$
$(1+i)^2=1+2i-1=2i$
$(1+i)^3=(1+i)(1+i)^2=-2+2i$
$(1+i)^4=((1+i)^2)^2=-4$
これらを複素平面にプロットすると...

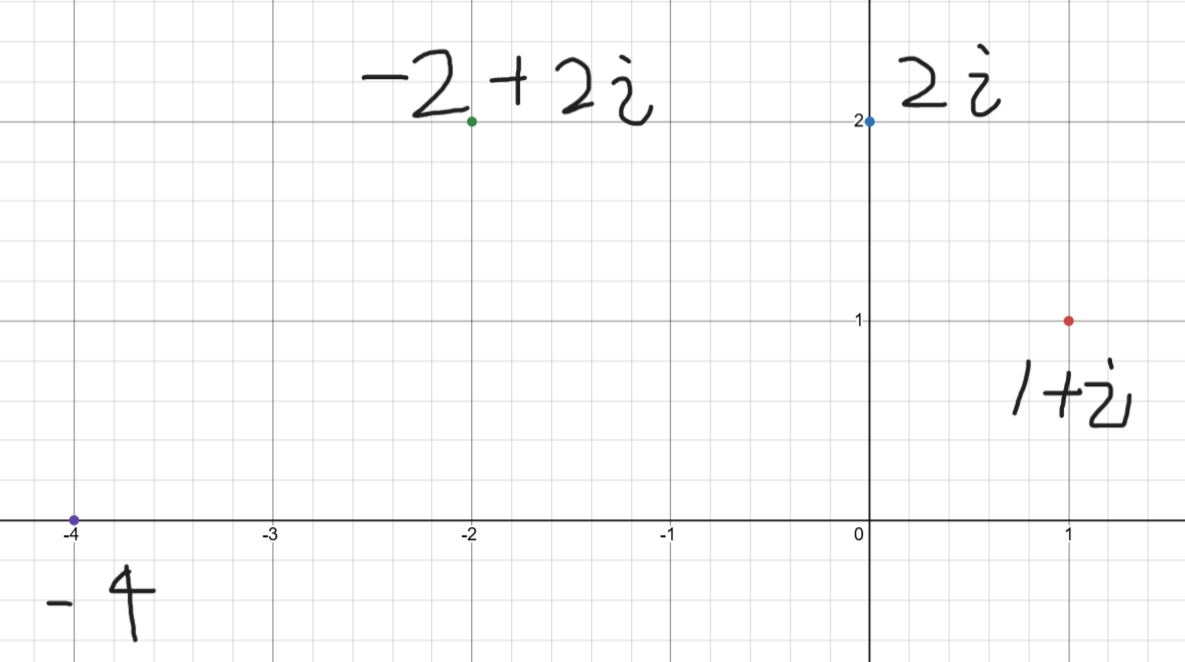
nが増えるにつれて原点の周りをくるくる回ってる！
原点からの距離と角度(x軸始点)で見てみると、

$(1+i)$は距離が$\sqrt2$で角度が$45$度
$(1+i)^2$は距離が$2$で角度が$90$度
$(1+i)^3$は距離が$2\sqrt2$で角度が$135$度
$(1+i)^4$は距離が$4$で角度が$180$度

...
距離は$\sqrt2$ずつかけ算してて、角度は$45$度ずつ足し算してる！

これからわかることは、

ある複素数に複素数$z$(距離$r$角度$θ$)をかけると、
距離が$r$倍になり、角度は$θ$をプラスする！

これから、

距離$1$($r=1$)の複素数の掛け算をすると原点中心に回転できる！！

$x^n=1$の秘密

$x^n=1$をいろんな$n$について解いてみよう！

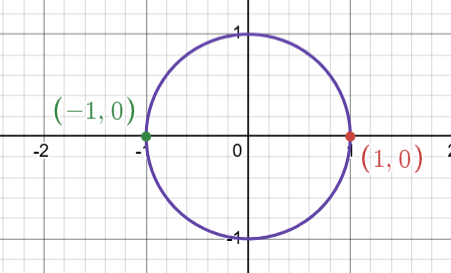
$x^2=1$

$x^2-1=0$
$(x-1)(x+1)=0$
$x=\pm1$

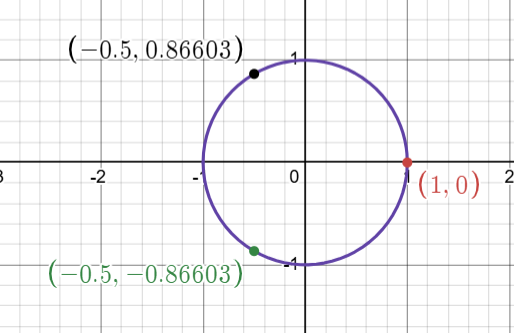
$x^3=1$

$x^3-1=0$
$(x-1)(x^2+x+1)=0$
$x=1,\frac{-1\pm\sqrt3i}{2}$

$x^4=1$

$x^4-1=0$
$(x^2-1)(x^2+1)=0$
$(x-1)(x+1)(x-i)(x+i)=0$
$x=\pm1,\pm i$

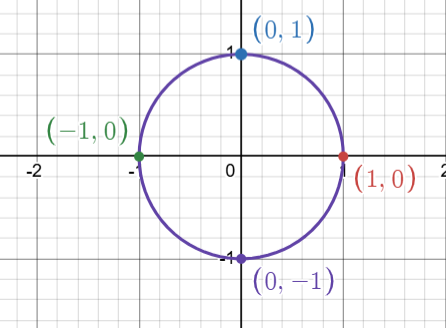
これらの複素平面上の点を見てみると

半径$1$の円周上に、$(1,0)$を中心に等間隔で並んでる！！

つないだら正$n$角形ができそう！！

でも、よくよく考えたら当たり前だ。
複素数の掛け算は距離は$×r$、角度は$+θ$だから
距離は$n$乗して$1$になる実数じゃないといけないし、
角度も$n$倍して$0(2nπ,nは整数)$にならなきゃいけないんだから。

例えば$n=3$
$r^3=1,r$は実数だから$r=1$
$3θ=0,2π,4π,6π,...$、$θ$は$0,\frac23π,\frac43π,2π,...$
$2π$から先はかぶってるから$θ=0,\frac23π,\frac43π$

距離$r$、角度$θ$の複素数は$r($cos$θ+i$sin$θ)$と表せれるから
$x^3=1$の解は
cos$0$+$i$sin$0$
cos$\frac23π$+$i$sin$\frac23π$
cos$\frac43π$+$i$sin$\frac43π$
の3つとわかる！！

点と点の角度を調べてみよう！

どんな複素数(距離$r$角度$θ$)をかけたかわかれば、
点と点の角度がわかるね！！

じゃぁ、$1+i$から$3i$まで！
$(1+i)×複素数z(距離r角度θ)=3i$
$z=\frac{3i}{1+i}$、、、分母の$i$を消すぞ！！
$z=\frac{3i(1-i)}{(1+i)(1-i)}=\frac{3+3i}2=\frac3{\sqrt2}(\frac{\sqrt2}2+\frac{\sqrt2}2i)$
$=\frac3{\sqrt2}($cos$\fracπ4+i$sin$\fracπ4)$