第3章 等角共役点と類似重心
①等角共役点
円上の点A,B,C,D,E,Fについて、AD,BE,CFが一点で交わるとき、
$\frac{AB}{DE}・\frac{CD}{FA}・\frac{EF}{BC} =1 $ (証明[29])
![線分が一点で交わるとき成立する。[29]](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2FQtSqJ1xVONaDJik9Zneg.png?alt=media)
線分が一点で交わるとき成立する。[29]
証明
$$
\frac{AB}{DE}=\frac{XA}{XE},
\frac{CD}{FA}=\frac{XE}{XC},
\frac{EF}{BC}=\frac{XC}{XA}
$$
$$
\frac{AB}{DE}・\frac{CD}{FA}・\frac{EF}{BC}=\frac{XA}{XE}・\frac{XE}{XC}・\frac{XC}{XA}=1
$$
よって成立する。
円上の点A,B,C,D,E,Fについて、
$\frac{AB}{DE}・\frac{CD}{FA}・\frac{EF}{BC} =1 $
のときAD,BE,CFが一点で交わる。 (証明[29])
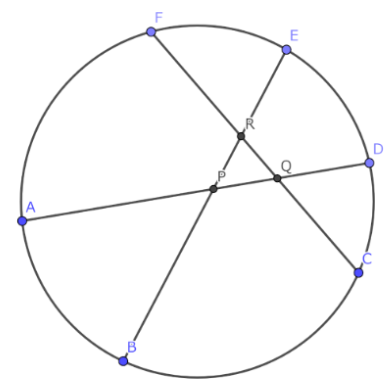証明に用いる図
AD,BE CF,DA EB,FCの交点をそれぞれP,Q,Rとし、並び順はこの通りとする。
(文字を入れ替えてこの形にできる)
$\frac{AB}{DE}・\frac{CD}{FA}・\frac{EF}{BC} =1 $
のとき、$$
\frac{AB}{DE}=\frac{PA}{PE},
\frac{CD}{FA}=\frac{QC}{QA},
\frac{EF}{BC}=\frac{RE}{RC}
$$だから、
$$
\frac{PA}{PE}・\frac{QC}{QA}・\frac{RE}{RC}=1,
\frac{PA}{QA}・\frac{QC}{RC}・\frac{RE}{PE}=1
$$図より、
$ \frac{PA}{QA}≦1,\frac{QC}{RC}≦1,\frac{RE}{PE}≦1$
等号成立のために、P,Q,Rは一致する。よって示せた。
角の頂点を通る直線 l と角の二等分線に関して対称な直線 m を l の等角共役線という。
AP,BP,CP の等角共役線は一点で交わり，これを P の等角共役点という。
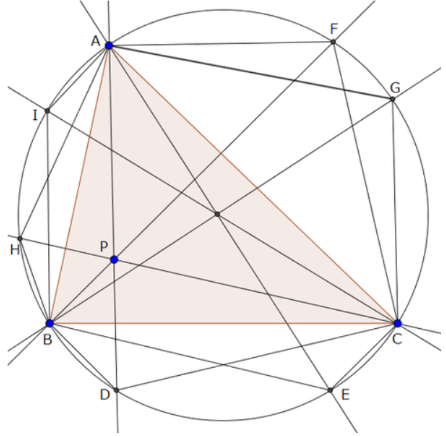証明に用いる図 弦チェバをもちいる
AP,BP,CPと外接円の交点の、A,B,Cでない方をD,F,Hとする。
AP,BP,CPの等角共役線と外接円の交点の、A,B,Cでない方をE,G,Iとする。
弦チェバより
$\frac{BD}{DC}・\frac{CF}{FA}・\frac{AH}{HB}=1$
図より弦に対する角が等しいから、BD=EC,BE=DC,CG=FA,CF=GA,AI=HB,AH=IB
よって$\frac{EC}{BE}・\frac{GA}{CG}・\frac{IB}{AI}=1$
弦チェバの逆より、
AP,BP,CPの等角共役点は一点で交わる。
②逆並行
三角形ABCについて、B,C,D,Eが同一円上であるとき、DEはBCに逆並行であるという。
これはΔABC∽ΔAEDと同値である。
![図3-5 DEはBCの逆平行線である。[31]](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2FlBkpyvGvsnU6en4KR9jz.png?alt=media)
図3-5 DEはBCの逆平行線である。[31]
ΔABCについて、Aを通るある直線は、ΔADEの等角共役線になる。
BC上にFをとり、AGをAFの等角共役線とし、H,IをBCとAF,AGとの交点とすると、ΔABC∽ΔAEDで、∠BAF=∠EAIより、ΔBAF∽ΔEAI
よって、AFとAIは相似より、対応する直線である。∠DAH=∠EAIよりAH,AIは等角共役線だから題義が示された。
垂足三角形の各辺は、元の三角形の各辺と逆並行である。
垂足三角形より、∠BEC=∠BFC=90°だから、円周角の定理の逆より、B,C,E,Fは同一円上であるため、EFはBCに逆平行である。FD,DEについても言える。よって示せた。
③類似中線
③類似中線はほとんど全て[32]から引用した項目である。
類似中線は、中線の等角共役線である。
三角形ABCについて、ADは類似中線である。
このとき、AD上に点Gを取るとGH:GI=AB:AC
ADは類似中線だから、ΔAGI∽ΔAME、ΔAGH∽ΔAMFである。よって、GH:GI=MF:ME Mは中点だから、ΔABM=ΔACMしたがってAB・EM=AC・FM MF;ME=AB:AC
三角形ABCについて、ADは類似中線であるとすると、
BD:CD=AB^2:AC^2
BD:CD=ΔABD:ΔACD=AB・DF:AC・DE
ここで類似中線の性質①より、
DF:DE=AB:AC よって成立
この本を高評価した人
この本に送られたバッジ
投稿者
コメント
他の人のコメント
