第二章 オイラー・ナーゲル座標
 スチュワートの定理
スチュワートの定理
∠B,∠C<90°、AからBCに下した垂足をHとし、PがC,Hの(端点を含む)間だと仮定する。
(PがB,Hの間でもB,Cを入れ替えて同様の議論ができる)
c^2=(BP-PH)^2+AH^2=BP^2-2BP・PH+PH^2+AH^2=AP^2+BP^2-2BP・PH
b^2=(CP+PH)2+AH^2=BC^2+2CP・PH+PH^2+AH^2=AP^2+CP^2+2CP・PH
2PH=(AP^2+BP^2-C^2)/BP=(b^2-AP^2-CP^2)/CP
CP(AP^2+BP^2-C2)=BP(b^2-AP^2-CP^2)
(CP+BP)AP2+(CP+BP)CP・BP=b^2BP+c^2CP
AP^2=(BPb^2+CPc^2)/(BP+CP)-BP・CP
定義よりBP:CP=m:nだから、示せた。
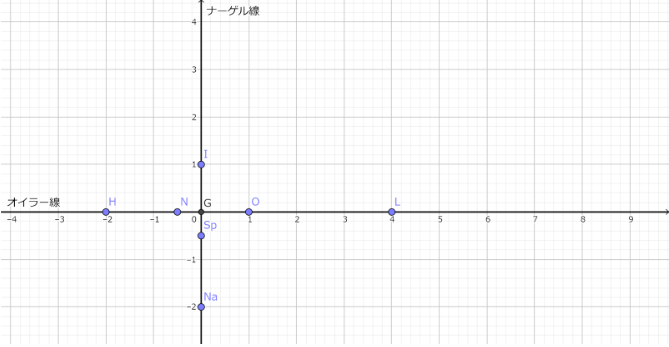 これこそがオイラー・ナーゲル座標である!
これこそがオイラー・ナーゲル座標である!
任意の三角形のオイラー線、ナーゲル線をそれぞれx軸、y軸として平面を作り、重心を(0,0),内心を(0,1),外心を(1,0)定義して得られる座標。
注意 EN座標は直交座標ではなく、斜交座標である。
これまでにでてきた点は、ほぼ全て座標上に表せる。
垂心(-2,0) 九点円の中心(-0.5,0)
ナーゲル点(0,-2) シュピーカー点(0.-0.5) ドロンシャン点(4,0)
①EN座標の活用その1
ベバン点は傍心三角形の外心とする。
①外心は内心とベバン点の中点
②ベバン点はナーゲル点とドロンシャン点の中点
③スピカー点は垂心とベバン点の中点 [24]
ベバン点はX(40)である。
この証明を愚直に行うのは困難だが、EN座標用いて容易に証明できる。
ΔABCの傍心三角形をΔDEFとしたら、
ΔABCはΔDEFの垂足三角形である(傍心三角形の性質①) よって、
ΔABCの内心=ΔDEFの垂心(垂足三角形の性質①)
ΔABCの外心=ΔDEFの九点円の中心(九点円の定義)
ΔABCのベバン点=ΔDEFの外心(ベバン点の定義)
ここでΔDEFにおいて九点円の中心は垂心と外心の中点だから、
ΔABCにおいて外心は内心とベバン点の中点である。
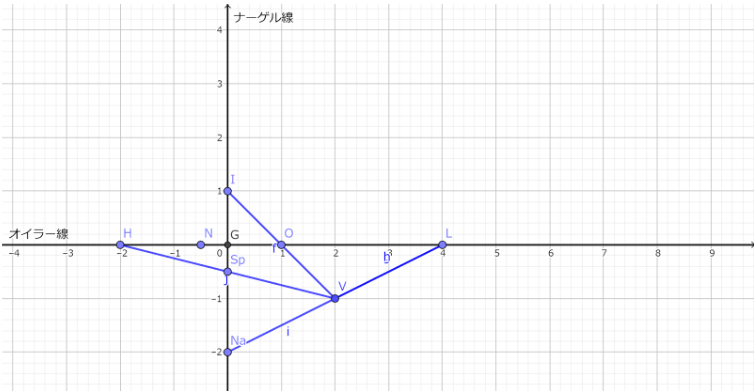 Vがベバン点である。
Vがベバン点である。
①からEN座標においてベバン点が(2,-1)であると分かる。
EN座標のおかげで②③を証明できた。
②EN座標の活用その2
三角形ABCの任意の点Pと重心Gの距離は,
PG^2=(PA^2+PB^2+PC^2)/3-(a^2+b^2+c^2)/9
で表せる。
[25]から着想をえた。重心のもう一つの強力な性質を用いて、EN座標上の任意の点同士の距離を導出できる。これが意味するのは
①各頂点との距離二乗の和が最小にする点は、重心である。
(PA^2+PB^2+PC^2を最小にするのはPG=0 よってPが重心のとき)
②Pと各頂点の距離が分かると、PGが分かる
③PA^2+PB^2+PC^2=(a^2+b^2+c^2)/3 等号成立条件は、Pが重心のとき。
④PA^2+PB^2+PC^2が一定の点の集合は、重心Gを中心とする。円になる。
⑤平面xyに対してPA^2+PB^2+PC^2を表すz座標を用意すると、重心を中心とするすり
鉢状の図形が生まれる。(重心ありじごくと呼んでいる理由)
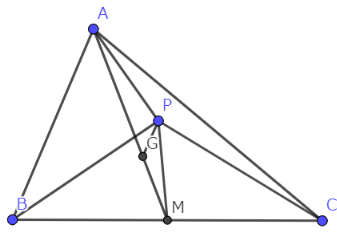 中線定理とスチュワートの定理が使える。
中線定理とスチュワートの定理が使える。
 証明の流れ
証明の流れ
重心ありじごくの活用
①外心
OG^2=R^2-(a^2+b^2+c^2)/9 ※外接円の半径を、Rとする。
Pが外心のとき、PA^2=PB^2=PC^2=R^2
よってPG^2=R^2-(a^2+b^2+c^2)/9が成立する。
★参考 ライプニッツの不等式 a^2+b^2+c^2≦9R^2
もちろん重心ありじごくP=外心で導ける。
②内心
※内接円の半径をrとする。
IG^2=(IA^2+IB^2+IC^2)/3-(a^2+b^2+c^2)/9
 補足
補足
AIとBCの交点をDとする。角の二等分線の公式よりAI:IP=b+c:a,AI^2:AP^2=(b+c)^2:(a+b+c)^2 スチュワートの定理の角の二等分線版より、
AD^2=bc-a^2bc/(b+c)^2
AD^2=bc(a+b+c)(-a+b+c)/(b+c)^2 IA^2=bc(-a+b+c)/(a+b+c)
IB,ICについても同様に示せる。
これよりIGの長さが分かるようになった。
③九点円の中心
内接円の半径がr,九点円の半径がR/2,フォイエルバッハの定理より、
IN=R/2-r
IO^2=R(R-2r) (証明[26])
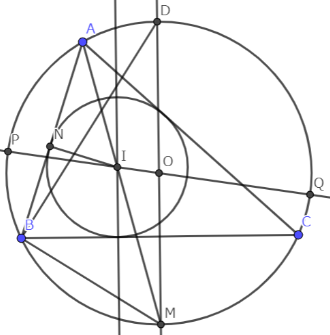 二つの三角形が相似であることを利用して証明する。
二つの三角形が相似であることを利用して証明する。
MをAIと外接円の交点、DはOMと外接円の交点、NはABと内接円の接点、P,QをOIと外接円の交点とする。dをIOの長さとする。
①∠BIM=∠BAM+∠ABI=∠MAC+∠IBC
=∠MBC+∠IBC=∠IBM よって△BIMは二等辺三角形であり、IM=BM
②円周角の定理より ∠NAI=∠BDM
直径に対する円周角より ∠ANI=∠DBM=90°
二角相等より、ΔANI∽ΔDBM よって AI:DM=NI:BM AI×BM=DM×NI
これらの議論から
(R-d)(R+d)=PI×IQ
=AI×IM (方べきの定理)
=AI×BM (①)
=DM×NI (②)
=2Rr R^2-d^2=2Rr OI^2=R(R-2Rr)
これらの情報と、EN座標を組み合わせて、EN座標上の任意の2点間の距離を求められる。
EN座標上の任意の2点間の距離を求めるプロセス
1.外接円の半径と、内接円の半径を求める
2.①②とオイラーの等式をから導けたGO,GI,IOの値を余弦定理に代入し
オイラー線とナーゲル線のなす角を求める
3.EN座標を用いて、余弦定理で2点間の距離を求める
(例)
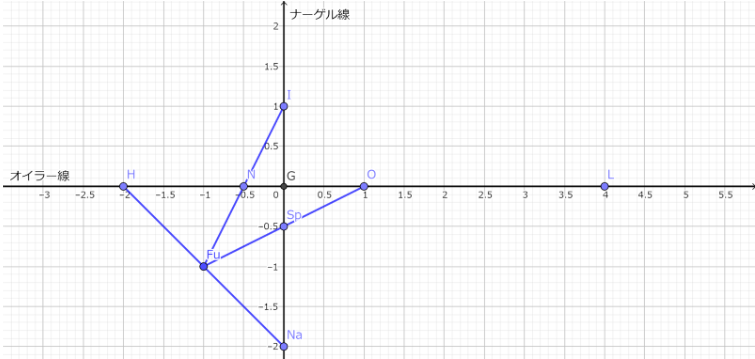 Fuがフールマン点である。
Fuがフールマン点である。
フールマン円は、垂心とナーゲル点を直径とする円である。
フールマン円の中心をフールマン点 Fuとする。 (X(355)) [27]
フールマン点は垂心とナーゲル点の中点である。 EN座標が(-1,1)であることは
分かっているため、①から②、③を示せる。
フールマン円の半径を求めよ。
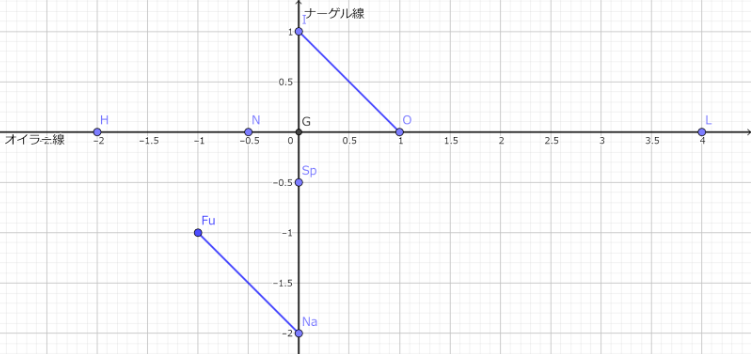 FuNaがフールマン円の半径にあたる。
FuNaがフールマン円の半径にあたる。
[解答]
EN座標により FuNaとIOは同じ長さである。
オイラーの定理から 答え √(R(R-2r))
次の長さを求めよ
1.ONaの長さ
2.VFuの長さ
[解答]
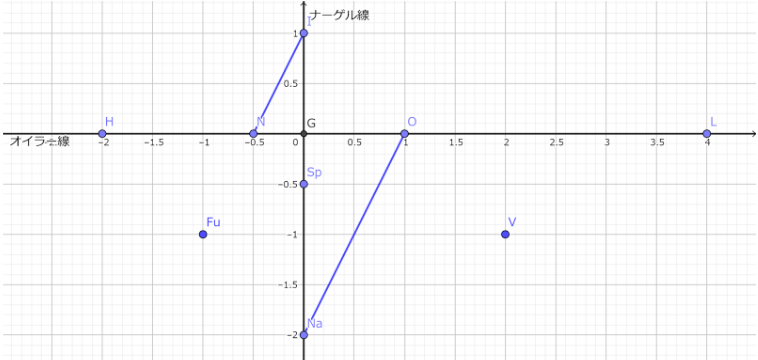 ONaはINの二倍である。
ONaはINの二倍である。
1.EN座標を使うことで、ONaはINの倍の長さであることがわかる。
だから、2・R/2-r=R-2r 答え R-2r
2.EN座標を使うことで、FuVとHOは平行かつ長さが等しいことがわかる。
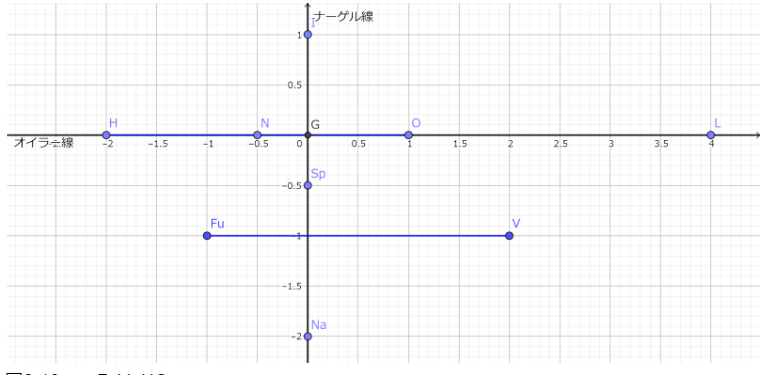 FuV=HO
FuV=HO
FuV=HO=3GO
GO=√(R^2-(a^2+b^2+c^2)/9) だから、
答え 3√(R^2-(a^2+b^2+c^2)/9)
★EN座標Extra
①出てくる直線
EN座標(x,y)において、
オイラー線 y=0
ナーゲル線 x=0
ソディ線 -x/4+1 と表せる。ソディ線はこの論文では紹介しない
②中点三角形、オイラー三角形とEN座標
1.EN座標(x,y)で表せる点が中点三角形にあるとき、それは元の三角形の(-x/2,-y/2)である。
2.EN座標(x,y)で表せる点は、中点三角形の(-2x,-2y)である。
3.EN座標(x,y)で表せる点がオイラー三角形にあるとき、それは元の三角形の(x/2-1,y/2)である。
4.EN座標(x,y)で表せる点は、オイラー三角形の(2x+2,2y)である。
③ EN座標とETC
[28]にいろいろな三角形の中心が掲載されている。実にEN座標はETCにのっているあらゆる点を表現できるのだ。
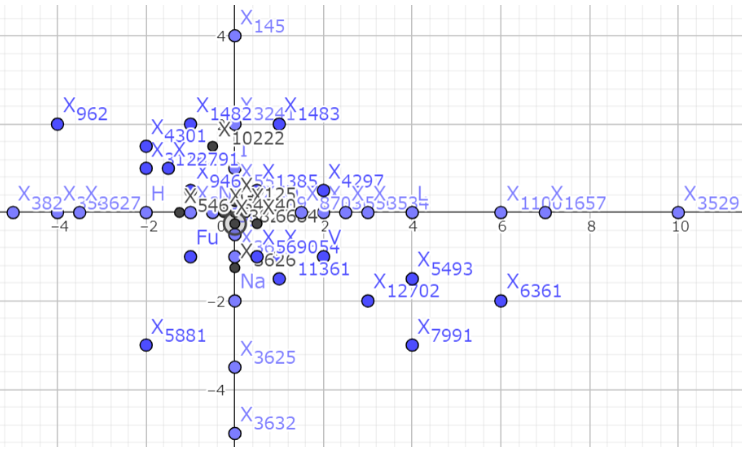 これがEN座標の真髄である。
これがEN座標の真髄である。
この本を高評価した人
この本に送られたバッジ
投稿者
コメント
他の人のコメント

