第1章三角形の基本的な点(前半)
第1章 三角形の基本の点まとめ
※ここからは特に言及しない場合、点をこのように示す。
 点の一覧
点の一覧
①五心とオイラー線
内心、外心、重心、垂心、傍心に関する知識を前提に話を進める。[4]
三角形の外心、重心、垂心は同一直線上であり、OG:GH=1:2である。外心、重心、垂心を通る直線をオイラー線という。(証明 [5])
②九点円の定理(既知)
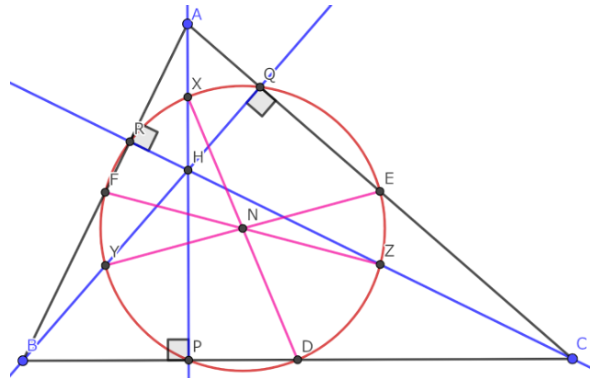 赤い円が九点円である。ピンクの線分は九点円の直径である。
赤い円が九点円である。ピンクの線分は九点円の直径である。
ΔDEFをΔABCの中点三角形、ΔPQRをΔABCの垂足三角形、ΔXYZをΔABCのオイラー三角形という。この定理より、中点三角形、垂足三角形、オイラー三角形のそれぞれの外心は元の三角形の九点円の中心と一致する。
![オイラー線上の線分比を表す[7]](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2FLBVq5ezR9pMR7lTDrgFx.png?alt=media) オイラー線上の線分比を表す[7]
オイラー線上の線分比を表す[7]
九点円の中心NはOHの中点であり、オイラー線上にある。(証明[8])
三角形において その九点円は 内接円に内接し 傍接円に外接する。(証明[9])
フォイエルバッハ点(X(11))の定義
九点円と内接円の接点を、フォイエルバッハ点とする。
![九点円(紫)は内接円(赤)と傍接円(青)に接する。[10]](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2F64yMDlWP5Jt69H5QAo6c.png?alt=media) 九点円(紫)は内接円(赤)と傍接円(青)に接する。[10]
九点円(紫)は内接円(赤)と傍接円(青)に接する。[10]
★3つの円に接する円をアポロニウス円という
(アポロニウス円の定義は沢山あるためややこしい)
九点円は、3つの傍接円に内接するため、3つの傍接円のアポロニウス円の一つである。
ということは、3つの傍接円に外接する円もかける。その中心はX(970)である。
![赤がアポロニウス円である。[11]](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2FvYGLqT75Z1axG8KmAboO.png?alt=media) 赤がアポロニウス円である。[11]
赤がアポロニウス円である。[11]
他にも九点円にはシムソン線や直交双曲線に関わる面白い性質がある。[12]
③中点三角形
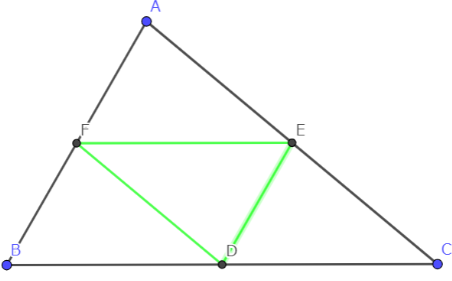 図1-5 緑色の三角形が中点三角形である。
図1-5 緑色の三角形が中点三角形である。
中点三角形の定義
三角形の各辺の中点をつないだ三角形を中点三角形とする。
ある三角形の重心とその中点三角形の重心は一致する。
ある三角形とその中点三角形は相似(homostic)であり、相似比は2:1、相似の中心は重心である。
証明は第5章のはじめを参照
この定理から分かること
①ある三角形ABCのP,Q (「三角形の中心」)について、ΔDEFが中点三角形のとき、
ΔDEFのPがΔABCのQであること、PG:GQ=2:1は同値である。
②ある三角形とその中点三角形のそれぞれの線ℓが一致することと、
ℓが重心を通ることは同値である。
重心の特性定理①の活用
中点三角形の垂心は元の三角形の外心である。
【証明】 HG:GO=2:1だから、重心の特性定理①より示された。
九点円の半径はR/2である。ただしRは外接円の半径
【証明】 ある三角形とその中点三角形は相似であり、相似比は2:1だから、示される。
④垂足三角形(だいたい既知)
ΔABCについて、D,E,FをA,B,Cの垂足とすると、ΔDEFをΔABCの垂足三角形という。
垂足三角形には面白い性質が沢山ある。順番に紹介しよう。
※ΔABCについて、「AからBCに下した垂線の足」を省略して「Aの垂足」としている。
![青い三角形が垂足三角形[13]](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2Ff2KzLQOjyhSLfFc4NwNN.png?alt=media) 青い三角形が垂足三角形[13]
青い三角形が垂足三角形[13]
鋭角三角形の垂心 は,その垂足三角形の内心と一致する。
垂足三角形の性質②
鈍角三角形の垂心は,その垂足三角形の傍心と一致する。
(両方とも証明[13])
![青い三角形が垂足三角形である。[13]](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2FdQccQYOfoLfwPY7EYk9W.png?alt=media) 青い三角形が垂足三角形である。[13]
青い三角形が垂足三角形である。[13]
△ABCの垂足三角形を△DEF, 垂心をHとする。 △ABD∽△CBFより∠BAD=∠BCF …(1) □AFHEは円に内接するから、∠BAD=∠HEF …(2) □HDCEは円に内接するから、∠BCF=∠HED …(3) (1), (2), (3) より∠HEF=∠HED 同様に、∠HFE=∠HFD, ∠HDF=∠HDE であることが示されるから、 △ABCの垂心Hは△DEFの内心と一致する。
![青い三角形が垂足三角形である。[13]](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2FrrNrLOhw5pbt16IwLcNR.png?alt=media) 青い三角形が垂足三角形である。[13]
青い三角形が垂足三角形である。[13]
△ABCの垂足三角形を△DEF, 垂心をHとする。 △ABDは∠ADB=90°の直角三角形より∠BAD <90° △ABEは∠AEB=90°の直角三角形より∠ABE <90° △BHDは∠BDH=90°の直角三角形より∠BHD <90° よって△ABHは鋭角三角形で、△DEFはその垂足三角形になっているから、 FC, EC, DCはそれぞれ∠EFD, ∠FED, ∠FDEの内角の二等分線で、 また、EC⊥EH, DC⊥DHよりEH, DHはそれぞれ∠FED, ∠FDEの外角の二等分線であるから、Hは△DEFの傍心となる。
鋭角三角形に内接する三角形のうち、周の長さが最小になるものは垂足三角形である。
&&&thm 垂足三角形の性質③
鋭角三角形に内接する三角形のうち、周の長さが最小になるものは垂足三角形である。(証明[13])
BC上に点Dを固定し、ABに関してDと対称な点をP, ACに関して対称な点をQとすると、DF+FE+ED=PF+FE+EQ よりP, F, E, Qが一直線になるとき△DEFの周は最小になる。
次に、点DがBC上を動くとき△DEFの周(=PQ)を最小にするには、
∠PAQ=2∠BAC(一定), AP=AQ=ADより、ADを最小にすればよく、それはAD⊥BCとなるときである。
同様に、E, FについてもBE⊥CA, CF⊥ABとなるとき△DEFの周の長さを最小にするから、
△ABCの垂足三角形が求める三角形となる。
![[13]](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2FUMTovglrwnFj0tO259aR.png?alt=media) [13]
[13]
鋭角三角形△ABCの面積をS, 外接円の半径をRとすると、
ΔABCの垂足三角形の周の長さは2S/Rに等しい。
納得のいく証明が見つからなかったから自力で証明した。

⑤傍心三角形
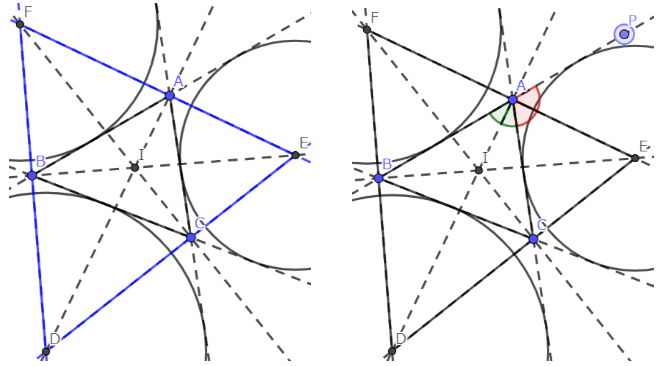 (左)DEFが傍心三角形である。(右)垂足三角形との関連性の証明
(左)DEFが傍心三角形である。(右)垂足三角形との関連性の証明
三角形の3つの傍心がなす三角形を、傍心三角形という。
傍心三角形の性質 三角形ABCの傍心三角形を三角形DEFとすると、ΔABCはΔDEFの垂足三角形である。
線分ABのA側の延長線上に点Pをとる。
傍心Dは∠BACの二等分線上で傍心Eは∠CAPの二等分線上にある。
90°=1/2∠BAP=1/2(∠BAC+∠CAP)=1/2∠BAC+1/2∠CAP=∠DAC+∠EAC=∠CAE
よってAはDからEFに下した垂足である。同様の性質をB,Cで示し、ΔABCはΔDEFの垂足三角形であると分かる。
⑥オイラー三角形
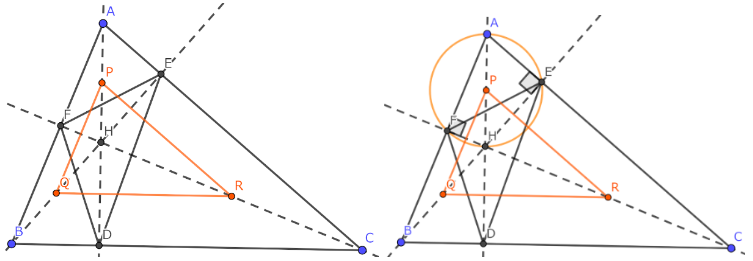 (左)オレンジの三角形がオイラー三角形である。(右)証明に用いる図
(左)オレンジの三角形がオイラー三角形である。(右)証明に用いる図
垂心と各頂点の中点をつないでできる三角形を、オイラー三角形とする。
ΔABCの垂足三角形をΔDEFとすると、ΔAEF、ΔBFD,ΔCDEの外心はオイラー三角形の頂点である。
∠AFH=∠AEH=90° 円周角の定理の逆よりA,E,F,Hは同一円上であり、その中心はA,Hの中点になる。この点はオイラー三角形の頂点だから、示せた。
ある三角形とそのオイラー三角形は相似(homostic)であり、相似の中心は垂心である。
[証明]第5章参照
![三本のオイラー線が青線であり、青い点が X(125)である。[14]](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2F7sKnspoIyHPJIdWLj7em.png?alt=media) 三本のオイラー線が青線であり、青い点が X(125)である。[14]
三本のオイラー線が青線であり、青い点が X(125)である。[14]
三角形ABCの垂足三角形をΔDEFとし、ΔAEF,ΔBFD,ΔCDEのオイラー線は九点円上の一点で交わる。この点はX(125)(Jerabek双曲線の中心)である。
Wolfram Mathworldには載っているが、「九点円」と調べても出てこない、九点円の隠された性質である。
この本を高評価した人
この本に送られたバッジ
投稿者
コメント
他の人のコメント

