文献あり

記法と注意（特に部分多様体）

141

記法と注意

（$C^\infty$級）多様体には連結性と第二可算性を課す。単射ではめ込まれた部分多様体を単に「部分多様体」と呼び、「埋め込まれた部分多様体」とは区別する。
多様体（とその上の何か）に対するある性質が局所的であるとは、任意の開被覆$\{U_i\}$に対し「$\forall i\ U_i$で成立$\iff$全体で成立」となることとする。

記法

多様体は$M,N$、部分多様体は$\iota:P\hookrightarrow M$で表す。$k\leq n$は大抵その次元。
$C^\infty$級写像、$C^\infty$級関数は$\phi,\psi:M\to N$、$f,g:M\to\R$で表し、明記しなければ$C^\infty$級性を仮定する。
近傍はどの点の周りかを表して$U_p,U_q$などと書く。局所座標は$\tau,\sigma:U\to\R^n$などを使い、簡単のため像は常に$\R^d$全体とする。

部分多様体

$\iota:P\hookrightarrow M$についてはめ込み$\Leftarrow$単射なはめ込み$\Leftarrow$埋め込みという論理包含がある。ここではめ込みとは各点の微分が単射であることで、埋め込みとは更に像への同相を課したものであった。普通は後者を部分多様体と定めるが、Frobeniusの定理から来る積分多様体は埋め込みでないから真ん中を部分多様体と呼ぶ。もっと思い出すために簡単な例を軽く紹介する。

はめ込み not 部分多様体

自己交叉するものは全てこれである。

部分多様体 not 埋め込み

８の字のやつ（$\R$からの単射像だが原点近傍が無限遠方を含む。）
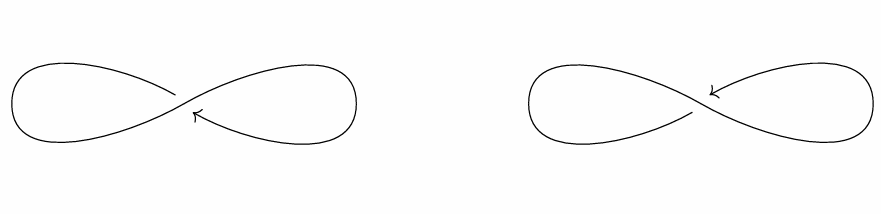８の字
トーラスにめっちゃ巻き付くやつ。$\iota:\R\ni t\longmapsto(\exp(2ti),\exp(2\alpha ti))\in \mathbb{T}^2$ を$\alpha\in\R\setminus\mathbb{Q}$について考えると、稠密になって滅茶苦茶な絵になる。
非可換回転
前者は悪い、後者は良い部分多様体である。これは$X:=\pdv{\theta_1}+\alpha\pdv{\theta_2}$というベクトル場の積分曲線であるが、Frobeniusの定理とは積分曲線の次元を上げた（つまり$k$個のベクトル場を積分してできる$k$次元の部分多様体）についての定理である。

部分多様体$\iota:P\hookrightarrow M$は単射だから、$\iota$とは$M$の部分集合$P$とその上の多様体構造の組と言ってもよい。しかし実際には$P\subset M$を指定するだけで「$\iota$が$C^\infty$級になる$P$上の多様体構造は一意」となることが多い。例えば、埋め込まれた多様体は普通（局所的に$\R^k\subset\R^m$に微分同相な）部分集合$P\subset M$として定まるが、実際そのような$P$についてはそうなっているため単なる部分集合として定義する。一般の部分多様体については次のような反例があるが、Frobeniusの定理から来る極大積分多様体は局所的に$\R^k\times\{\text{可算部分集合}\}\subset\R^n$と微分同相であるから、似た理由でこちらも正しい。

複数の多様体構造が入る部分多様体

$M:=\R^2,\ P$を８の字とする。図のように二通り$\R$からの$C^\infty$像だと思える：
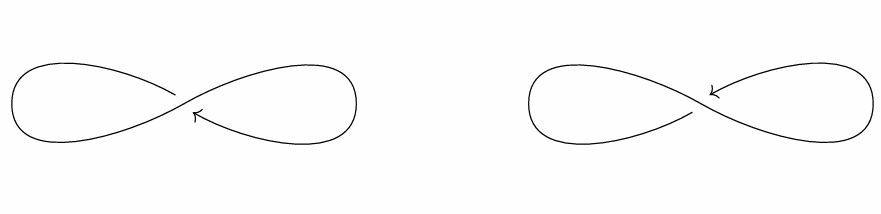８の字のやつ
が、$\iota'=\iota\circ\text{hoge}$となる$\R$の微分同相hogeは存在しない。

開集合への制限

開集合$U\subset M$と部分多様体$\iota:P\hookrightarrow M$に対し、$P\cap U:=\iota^{-1}(U)\hookrightarrow U$もそう。

これは当たり前なのだが、（$M$について）局所的な話に持ち込むときに有用。

多様体構造が一意的になる部分集合

まずは逆関数定理を呼び出す。どちらも、ある点の微分がopenな条件を満たす場合に局所的な標準形（自明な線形写像）の存在を保証する。

逆関数定理

$\phi:M\to N$と$p\in M,\ q:=\phi(p)$について
(1) 微分$d\phi_p:T_pM\to T_qN$が単射なら、ある局所座標$(U_p,\tau),(U_q,\sigma)$が存在し
$\R^k\xrightarrow[\tau^{-1}]{\cong} U_p\xrightarrow{\phi}U_q\xrightarrow[\sigma]{\cong}\R^n$を標準的な（線形）包含写像とできる。
(2) 微分$d\phi_p:T_pM\to T_qN$が全射なら、ある局所座標$(U_p,\tau),(U_q,\sigma)$が存在し
$\R^k\xrightarrow[\tau^{-1}]{\cong} U_p\xrightarrow{\phi}U_q\xrightarrow[\sigma]{\cong}\R^n$を標準的な（線形）全射とできる。

Frobeniusの定理で得られる積分多様体は次の仮定を満たすので、部分多様体を気にせず単に部分集合として書く。

この本の部分多様体は多様体構造が一意的

$P\subset M$が局所的に$\R^k\times\{\text{可算}\}\subset\R^n$に含まれるとする。つまり、$P$の各点$p$に対しある$M$内の局所座標$(U_p,\tau)$と可算部分集合$D\subset\R^{n-k}$が存在し、$\tau(U_p\cap P)\subset \R^k\times D$となっている。このとき、$P$が部分多様体となる（つまり$\iota:P\to M$が$C^\infty$級かつはめ込みとなる）多様体構造は一意的である。

スライス

ある局所座標$(U,\tau)$と$d\in\R^{n-k}$を用いて$S:=\tau^{-1}(\R^k\times\{d\})$と書ける部分集合$S\subset M$をスライスと呼ぶ。

$P$上の部分多様体構造を固定する。$\iota:P\to M$に対し逆関数定理を用いることで、各点$p\in P$に対し$P$に含まれるスライス$S\subset M$が存在し、そのような開集合$S$と$S\cong\R^k$全体がアトラスとなる。しかし、全てのスライス$S\subset P$がその$P$の部分多様体構造の局所座標となるわけではなく、あくまでそいつらの一部が開被覆になるというだけである（８の字参照）。というわけで示すべきことは「（アトラスに）一部を許せば全部入る」である。
実際に示すのはもっと強い命題である（$N=P$とすれば、$\id:P\to P$がどんな二つの多様体構造についても$C^\infty$級になる）。

自動的$C^\infty$級性

$P\subset M$が上の仮定を満たすとする。$P$を部分多様体とする多様体構造を一つ固定する。$\phi:N\to P$が$\phi:N\to M$として$C^\infty$級なら元の$\phi$も$C^\infty$級性。

$C^\infty$級性が局所的性質という理由で、$M=\R^n, P\subset\R^k\times D$として良い。$\R^k\times D$は$D$の位相を忘れれば自明な多様体構造（と位相）が入るが、これは$\R^n$からの相対位相よりも細かい。「$P$が$\R^n$の部分多様体ならこの位相について開」と「開なら自動的$C^\infty$級」に分けて示す。
まず、$S\subset P$となるスライスは連結性からある$d\in D$で$S\subset\R^k\times\{d\}$となる。これは微分が消えてない$\R^k$から$\R^k$への話だから、$S\subset\R^k\times\{d\}$は開である。故に一つ目（とついでに$P$が$\R^k\times D$から誘導される多様体構造を持つこと）が分かる。
二つ目は$N$が連結な場合に示せばいい。同じ理由で$\phi(N)$は$\R^k\times\{{}^\exists d\}$に含まれているとしていい。普通の微積分の話で「$\R^n$を終域として滑らかなら$\R^k(\subset\R^n)$を終域として滑らか」である。

[War]では「$P$上の位相を決めれば部分多様体とする多様体構造が一意」とかも示していた。

参考文献

[1]

Frank W. Warner, Foundations of Differentiable Manifolds and Lie Groups, Graduate Texts in Mathematics, Springer New York, NY, 1983, 276

[2]

森田　茂之, 微分形式の幾何学, 岩波書店, 2005, 372

[3]

Gijs M. Tuynman., An elementary proof of Lie’s Third Theorem., Publications de l’U.E.R. Mathematiques Pures et Appliquees, I.R.M.A. Univ. Lille, 1994, 4

投稿日：8月29日

更新日：9月1日