Frobeniusの定理
積分曲線の高次元化
この頁を書く前までは計算をしない証明の方がいいと思っていましたが、素朴な感覚を上手く証明に落とし込めなかったので、Morの2章の証明を読んだ方が良いかもしれません（唯一この頁の「直感的な説明」だけは価値があると思いますが）。
ベクトル場$X$の積分曲線$\gamma:(-\ve,\ve)\to M$とは$\dv{t}\gamma=X_{\gamma(t)}$を満たす曲線のこと。
$M$の各点に対しそこを通る積分曲線が存在し一意である、ODEの局所解の定理。
これの高次元版が積分多様体である。つまり、$k$個のベクトル場が与えられたらそれらを「積分」してできる部分多様体が存在したり存在しなかったりするのである。ただし、$k$個のベクトル場$X_1,\dots,X_k$として扱うのではなく、$D_x:=\span\qty{(X_1)_x,\dots,(X_k)_x}$という「各点に接空間の部分空間を滑らかに与えたもの」として扱う。これは$D$とは局所的には$M$からGrassman多様体$\Grass(n,k)$への写像だと思ってこれが$C^\infty$級と言っても、局所的には$k$個のベクトル場が$D_x$の基底になることと言っても、単に接束$TM$の部分束と言っても同じことである。こういう$D\subset TM$を分布と呼ぶ。
$\iota:P\hookrightarrow M$が分布$D$の積分多様体であるとは、各$p\in P$に対し$d\iota_p(T_pP)=D_{\iota(p)}$となること。今頁より後は$\iota$を省略して単に$P\subset M$と書くが、はめ込まれた部分多様体である（が色々大丈夫という話が前頁の結論だった）。
分布$D$とベクトル場$X$に対し、$X\subset D\overset{def}{\iff}\forall x\in M\ \ X_m\in D_m$と書く。
このとき、$D$が包合的とは$X,Y\subset D\Rightarrow [X,Y]\subset D$なること。
$X\subset D$は局所的な条件だから包合性も局所的である。特に、分布$D$の局所的な基底$X_1,\dots,X_k$を用いると、$X\subset D$とは「$X$が$C^\infty$級関数環係数で$X_i$の線形結合と書けること」、$D$が包合的とは「$[X_i,X_j]$が$X_k$の線形結合と書けること」である。リー環の場合は$\C$係数でこれが成り立ってるから次の定理から何らかしら多様体が取れる（実はリー群になる）というのが次頁のネタバレ。
$M$の各点に対しその点を通る積分多様体が存在$\iff$包合性
右から左が本質的だが、次の図から同値が直感的に分かると思う。
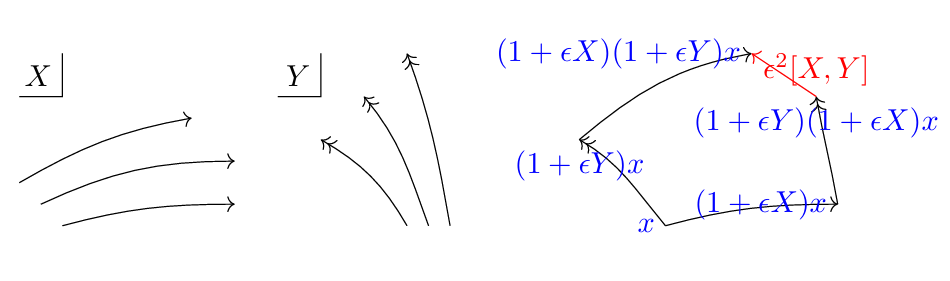ベクトル場に沿って貼り合わせる図
まず、$[X,Y]$とは、$X,Y$の非可換性を表す量であった。時刻0で$x$を通る$X$の積分曲線の時刻$\ve$での点を$(1+\ve X)x$と書くと、$(1+\ve X)(1+\ve Y)x$と$(1+\ve Y)(1+\ve X)x$は一般には一致せず、その差が$\ve^2[X,Y]_x$くらいになる。
積分曲線とはベクトル場の矢印をなぞって曲線を描く操作だったのと同様、積分多様体とは$D_x$という微小な正方形をペタペタ貼り合わせていく操作となる。このとき貼り合わせていく順番が問題となる。
まず、$X\subset D$に対し$D_x$を$D_{(1+\ve X)x}$に動かす操作は「スライド」するだけで「上下方向のズレ」は生じない（これは$X_x\in D_x$だから）。つまり、$D_x$と$D_{(1+\ve X)x}$は貼り合わされるべきである。故に$X,Y\subset D$のとき$D_x,D_{(1+\ve X)x},D_{(1+\ve Y)x},D_{(1+\ve X)(1+\ve Y)x},D_{(1+\ve Y)(1+\ve X)x}$は貼り合っていて、$D_{(1+\ve X)(1+\ve Y)x}$と$D_{(1+\ve Y)(1+\ve X)x}$に上下方向のズレはないから、さっきの議論とは逆に$\ve^2[X,Y]_x\in D_x$となる。これは「積分多様体があれば包合的」を意味するが、逆に包合的であれば微小な正方形を貼り合わせていく順番にほぼ依存しないから積分多様体を構成することができる（上下左右の二次元分の動きにより二次より大きい誤差は無視できる）。
前半
積分多様体の存在から包合性を言う。次の$\phi$-relatedは何故か便利。
$\phi:N\to M$と$N,M$上のベクトル場$X',X$が$\phi$-relatedとは$\forall x\in N\ \ d\phi(X'_x)=X_{\phi(x)}$なること。
このとき $(X',X)$と$(Y',Y)$が$\phi$-relatedならば$([X',Y'],[X,Y])$も$\phi$-related。
$[X,Y]f:=XYf-YXf$と微分作用素として定まっていたこと、上の条件は$\forall f\in C^\infty(M)\ \ X'(f\circ\phi)=(Xf)\circ\phi$と言い換えられることから計算ができる。
積分多様体$\iota:P\hookrightarrow M$と$X,Y\subset D$に対し、$X_{\iota(x)},Y_{\iota(x)}\in D_x=d\iota(T_xP)$ on $x\in P$から、$X_{\iota(x)}=d\iota(X'_x),Y_{\iota(x)}=d\iota(Y'_x)$となるように$P$上のベクトル場$X'_x,Y'_x$が局所的には取れる。局所的と言ったら今まで$M$の位相についてだったが、ここだけ$P$の位相についてである。
先の補題から$[X,Y]_{\iota(x)}=d\iota([X',Y']_x)\in d\iota(T_xP)=D_{\iota(x)}$ となる。初めの$P$を取り換え、全ての点での結論を得る。
後半
ベクトル場は非退化なら局所的な標準形を持つ。つまり$M$上のベクトル場$X$と$x\in M$に対し$X_x\neq0$なら$x$の局所座標$(U,\tau)$で$\tau_*X=\pdv{x_1}$とできる。
積分曲線は復習したが時間発展はしていないな、上では$1+\ve X$と書いたがちゃんと$\Phi:\R\times M\to M$の部分関数（$\{0\}\times M$の近傍でのみ定まる）$\Phi^t(x)$と書く。これの時間微分が$X$、つまり$\pdv{t},X$は$\Phi$-relatedである。$\Phi$を適当に$\R\times(\R^{n-1}\subset M)\cong\R^n$に制限すれば、逆関数定理から$\pdv{t},X$がある$\phi:\R^n\to M$で$\phi$-relatedになる。この逆写像が$\tau$。
$(\Leftarrow)$より少し強いことを示す。
包合的な場合、上の補題が高次元化できる。つまり包合的な$D$と$x\in M$に対しある局所座標$(U,\tau)$で$\tau_*D=\span\qty{\pdv{x_1},\dots,\pdv{x_k}}$となる。
故に積分多様体$\iota:P\to M$は$\iota(P)$が局所的に$\subset\R^k\times\{\text{可算}\}$となって、前頁から部分多様体構造が一意的になる。
「任意の多様体$M$とその上の$k$次元包合的分布$D$について主張が成立」という命題を$k$についての帰納法で示す。まず、$D$の局所的な基底$\qty{X_1,\dots,X_k}$を取る。局所座標を取って$X_1=\pdv{x_1}$とし、更に$X_i\mapsto X_i-X_i(x_1)X_1\ (i=2,\dots,k)$とすれば$X_i(x_1)=0\ (i=2,\dots,k)$とできる。
$S:=\{x_1=0\}$とすると、$dx_1(X_i)=X_i(x_1)=0$より$X_2,\dots,X_k$は$S$上のベクトル場だと思える。この$S$上のベクトル場が貼る$k-1$次元分布に対する帰納法の仮定から$S$上の局所座標$(x_2,\dots,x_k)$が取れる。勿論$S$上の座標だが、$X_1=\pdv{x_1}$の時間発展$\Phi^t$により$M$上の座標に延ばす。
$S_t:=\{x_i=t\}$と置く。どちらも$k$次元だから$\pdv{x_2},\dots,\pdv{x_k}\in D$を示せばいい（$\pdv{x_1}\in D$に注意）。$S=S_0$上では取り方そのものであり、それ以外の$S_t$ではその時間発展であること、つまり右辺の時間発展での整合性 $D=\Phi^t_*(D)$ を示す。
状況を整理し直すために一度証明を切る。
包含的な$D$と非退化な$X\subset D$に対し$\Phi^t_*(D)=D$となる。
ここで微分同相$\phi$に対し$\phi_*(D)_p:=d\phi(D_{\phi^{-1}p})$である。主張を示すためには$\Phi^t_*(D)_p$というグラスマン多様体（$T_pM$の$k$次元部分空間全体）内の曲線の微分が各$p$で至る時間消えていたらいいが、$(\phi\circ\phi')_*D=\phi_*\phi'_*D$なので$t=0$でのみ消えればいい。
もう全部局所の話なので、$M=\R^n,\ p=0,\ T_pM=\R^n$と諸々単純化しておく。曲線$D(t)\in\Grass(n,k)$の$t=0$での微分が消えていないとき$\xi(t)\in D(t)$で$\xi'(0)\notin D(0)$となる曲線が取れる（下注）。今の場合、$\xi(t)\in\Phi^{-t}_*(D)_p$であり、$Y(t):=d\Phi^t(\xi(t))\in T_{\gamma(t)}M$は$X$の積分曲線$\gamma(t)$に沿ったベクトル場である。$Y$の曲線近傍への拡張を同じく$Y$と書くと、$\xi'(0)=\pdv{t}\lvert_{t=0}\Phi^t_*(Y)_p=[X,Y]_p\in D_p$となって矛盾。
下注と書いたのは$\Grass(n,k)=\GL(n,k)/\GL(k)$という商（$\GL$とはfull rank行列全体の空間）の場合に接空間のレベルでも商になっているということから出るが、そういうことを感じながら具体的に基底を取って考えるともっと簡単に分かる。
極大積分多様体
積分多様体は最大なものが取れる。つまり、包合的な$D$と$x\in M$に対し次を満たす積分多様体$P\subset M$が存在し一意である：
$x$を通る積分多様体$P'\subset M$に対し、$P'\subset P$であり$P$の位相でこれが開。
$D$を標準化する局所座標$\tau$に付随するスライス全体をアトラスとすることで集合としての$M$にめっちゃ非可分な$k$次元多様体構造が生え、これの$x$の連結成分を$P$とすれば最大性がconnectedness argumentから出る。$P$の第二可算性は「高々可算次数のグラフの連結成分は高々可算」をやるのだが、ちゃんと書くと長くなってしまった。
$D$を標準化する局所座標$(U,\tau)$に対し付随するスライス$U(d):=\tau^{-1}(\R^k\times\{d\}),\ d\in\R^{n-k}$は積分多様体である。（不連結でもいい）積分多様体$P$について第二可算性から$P\cap U$が$\{U(d)\}_d$の可算個の和に含まれるので、前頁とその証明から$P$上の部分多様体構造が一意であることと$P\cap U(d)$が$P$の位相で開であるが分かる。特に、別のスライス$P=U'(d')$について、$U'(d')\cap U(d)$が$U(d)$内で開であることと$(U(d),\tau),(U'(d'),\tau')$の変換関数が$C^\infty$級であることが分かる。
これで必要な議論は全て尽くした（証明前のスケッチの意味が通る）のだが、もうちょっと書く。
$M$の可算アトラス$\{(U_i,\tau_i)\}$であって$D$を標準化するものを取る。$M$の部分集合$P$に対し、$P$と交わる全ての$U_i(d)$と$P$の合併を取る操作を考える。最初のステップでは$P$は$x$を含む適当な$U_i(d)$であり、この操作を有限回行っても上段の理由で高々可算個のスライスの和であり、全ての$n$回目についての合併を$P$とする。これは第二可算である。
この$P$には合併をした$(U_i(d),\tau)$全体としてアトラスが入る、これがちゃんと多様体になることは上に書いたことから分かる。
最大性について、勝手な積分多様体$P'$が$P'\subset P$と分かれば、$P$の位相で開であることは自動的である（自動的$C^\infty$級性と次元が同じはめこみが開写像であること）。さて、これは$P'$の連結性から分かるが、$P$を（スライスの交わりに関する）グラフの連結成分と定めた一方、$P'$の連結性は位相的な連結性なので注意が必要だ。しかし$P'$は弧状連結なので、$[0,1]$のコンパクト性によって、$P'$の任意の点は上の合併操作有限回で$x$から到達できる。
参考文献
この本を高評価した人
この本に送られたバッジ
投稿者
コメント
他の人のコメント
