複素関数と二次元の静電場

複素関数の基本

複素数は二次元の数

複素数は複素平面上のベクトルです。オイラーの公式を使った極形式で表せます。
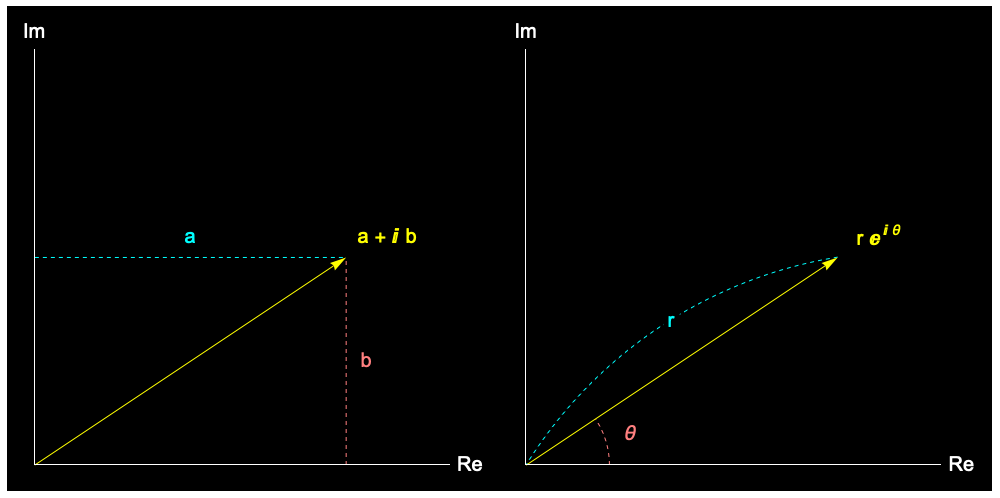複素数の普通の表示と極形式

複素数の演算は相似変換

複素数の加算は平行移動、乗算は拡大回転に対応します。この２つの操作は図形を相似に保ちます。
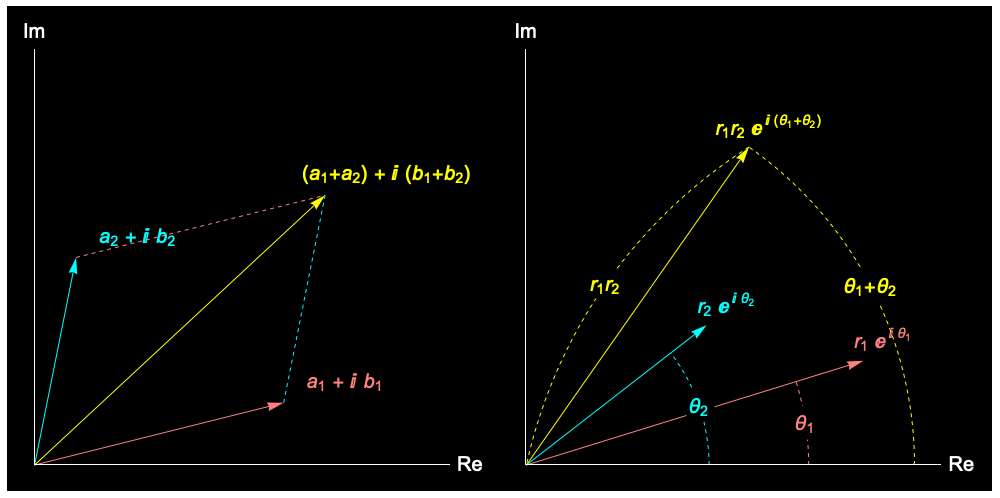加算は平行移動、乗算は拡大回転

複素関数は図形の変形

複素関数は二次元の図形を変形する操作とみなせます。
$f(z) = e^z$

複素関数の正則性

$w=f(z)$としたとき、$z$の微小変化に対する$w$の微小変化が、実数関数と同じように$dw = f'(z) dz $と表せることを正則性といいます。$f'(z)$は複素数なのでこの式は、$dw$は$dz$を拡大・回転したものであるという意味になります。複素数の演算の枠組みで微分を定義するには、$dz$と$dw$の関係はただの拡大・回転でなければならないということです。このため正則関数は微小正方形を微小正方形に移すことがわかります。
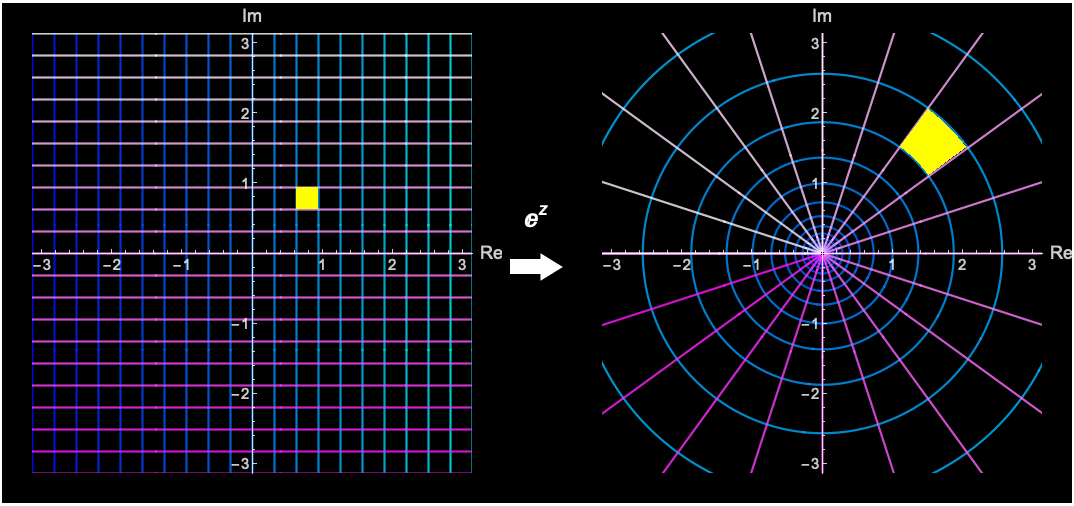正則性

コーシー・リーマンの方程式

複素関数が正則性をみたす条件がコーシー・リーマンの方程式です。
$z = x + i y$, $w = u + iv$ とします
\begin{eqnarray} dw &=& du + i dv = \left(\frac{\partial u}{\partial x} dx + \frac{\partial u}{\partial y} dy \right) + i \left(\frac{\partial v}{\partial x} dx + \frac{\partial v}{\partial y} dy \right) \end{eqnarray}
これが$(dx+ idy)$に複素数を掛けたものになっているためには、$(a+ ib ) (dx + i dy) = (adx - bdy) + i (b dx + ady)$という形になっているはずです。これから以下の式が得られます。

また以下のように考えることもできます。微小ベクトルの関係はヤコビ行列で表せます。
$$ \begin{pmatrix} du \\ dv \end{pmatrix} = \begin{pmatrix} u_x & u_y \\ v_x & v_y \end{pmatrix} \begin{pmatrix} dx \\ dy \end{pmatrix} $$
ヤコビ行列が拡大・回転であるためにはそれが
$$ r \begin{pmatrix} \cos \theta & - \sin \theta \\ \sin \theta & \cos \theta \end{pmatrix} $$
という形をしている必要があります。これからも同じ式が得られます。

ラプラス方程式

ラプラス方程式はこのような式です。
$$ \nabla^2 \phi = 0 $$

ラプラス方程式の歴史

まずニュートンが引力の法則を発見し、引力が距離の二乗に反比例すること、重ね合わせの原理が成り立つことを発見しました。この法則から、大きさを持った物体が及ぼす引力はそれを構成するすべての粒子からの力を積分することで得られます。ラプラスはこの力を位置の関数とした力の場を考え、この場が満たす方程式を示しました。それがラプラス方程式です。

引力の場が満たす方程式

まず力はベクトルなので、簡単にするためにスカラー関数であるポテンシャル関数$\phi(x,y,z)$を導入し、力をその勾配$\mathbf{F}=-\nabla \phi$で表します。距離$r$離れた粒子からの引力は$1/r^2$に比例するため、粒子が作るポテンシャルは$1/r$に比例します。粒子の位置を$(x',y',z')$とすると位置$(x,y,z)$に作るポテンシャルは
$$ \frac{1}{\sqrt{(x-x')^2+(y-y')^2+(z-z')^2}} $$
となります。このため大きさをもった物体が作るポテンシャルは以下のように表されます。
$$ V = \int \frac{dx'dy'dz'}{\sqrt{(x-x')^2+(y-y')^2+(z-z')^2}} $$
計算するとわかりますが、3次元では$\nabla^2 (1/r)=0$ なので
$$ \nabla^2 V = \frac{\partial V}{\partial x^2}+\frac{\partial V}{\partial y^2}+\frac{\partial V}{\partial z^2} = 0 $$
が成り立ちます。

流体の方程式

ラプラス方程式は流体の理論にも登場します。流体の中に仮想的な箱を考えます。その箱の中に流体が吸い込まれたり湧き出したりする点がない限り、箱の外から中に流入する流体の量と、中から外に流出する流体の量は同じになるはずです。微小な箱についてその内部から外部への流量を考えると発散という概念になり、各位置での流速を$\mathbf{v}$とすると、$\nabla \cdot v $と表せます。これがゼロのとき$\nabla \cdot \mathbf{v}= 0$となります。引力と同様にベクトルをスカラー場の勾配として表し、$\mathbf{v}= - \nabla \phi$とします。すると$\nabla^2 \phi=0$が成り立ちます。

ラプラシアンの意味

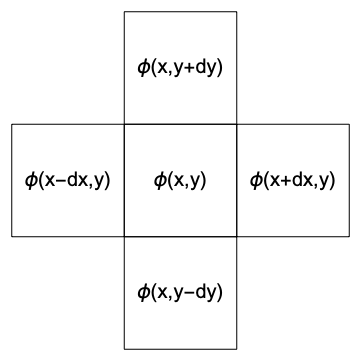微小領域
上図の領域について$\nabla^2\phi$を計算すると
\begin{eqnarray} \nabla^2\phi &=& (\phi(x+dx,y) - \phi(x,y)) - (\phi(x,y) - \phi(x-dx,y))/dx ~+ \\ && (\phi(x,y+dy) - \phi(x,y)) - (\phi(x,y) - \phi(x,y-dy))/dy \\ \end{eqnarray}
話を簡単にするため$dx=dy=1$とすると
$$ \nabla^2\phi=\phi(x+dx,y) + \phi(x-dx,y) + \phi(x,y+dy) + \phi(x,y-dy) - 4 \phi(x,y) $$となります。これから$\nabla^2 \phi=0$のとき、中央のセルは近傍のセルの値の平均値になります。セルの時間発展のプログラムとして、セルの値を周囲のセルの値の平均値にするという計算を各ステップ各セルに行わせると、以下の拡散方程式
$$\nabla^2 \phi=\frac{d\phi}{dt} $$
を解いているのと同じことになり、セルの値が周りに伝わっていくような計算ができます。ラプラスの方程式とはいわば、影響が周囲に均等に伝わることを表した式です。

グリーン関数

「影響が周囲に均等に伝わる」ことがラプラスの方程式とすれば引力の法則との関係はどうなるのでしょうか。三次元空間の一点からの湧き出しを考えたとき、その影響は球面に均等に分配されるはずです。これから流量は距離の二乗に比例して減衰することが導かれます。影響が空間を均等に伝わるということと、点からの影響が逆二乗で減衰することは同じことなのです。
　点からの影響がわかると、大きさをもったものの影響もそれを空間で積分することでわかります。グリーンはラプラス方程式の解法として、まず点からの影響を計算したグリーン関数というものを求め、それの重ね合わせで問題を解く方法を確立しました。
　位置$\mathbf{s}$にある微小粒子の場はデルタ関数$\delta(\mathbf{x} - \mathbf{s})$を使って
$$ \nabla^2 G(\mathbf{x},\mathbf{s}) = \delta(\mathbf{x} - \mathbf{s}) $$
を満たす$G$として求まります。$\rho(\mathbf{x})$が作る場はこの$G$を使って
$$ \int G(\mathbf{x},\mathbf{s}) \rho({\mathbf{s}}) d \mathbf{x} $$
と表せます。三次元の場合グリーン関数は$1/4\pi |\mathbf{x}-\mathbf{s}|$となり、２次元の場合$\ln |\mathbf{x}-\mathbf{s}|/2\pi$となります。この勾配をとると３次元では逆二乗の法則で減衰するベクトルが得られ、二次元では一乗の法則で減衰するベクトルになります。

ポアソンの方程式

電場についても同じ方程式が成り立ちます。電場は電位の勾配として$\mathbf{E}=-\nabla\phi\ $と表されます。電荷がないところで電位はラプラス方程式を満たします。電荷があるところでは右辺が有限になり、電荷密度を$\rho(\mathbf{x})$とすると$\nabla^2 \phi(\mathbf{x})=\rho (\mathbf{x})$を満たします。これをポアソンの方程式といいます。

電場を複素関数で表す

いま複素関数 $\phi + i \nu = f(x+i y)$ を考えるとコーシー・リーマンの方程式より$\phi,\nu$はラプラスの方程式を満たすことがわかります。また$\nabla \phi \cdot \nabla \nu = 0$ であることもわかります。このため、複素関数は２次元の電場を表す関数になりえます。

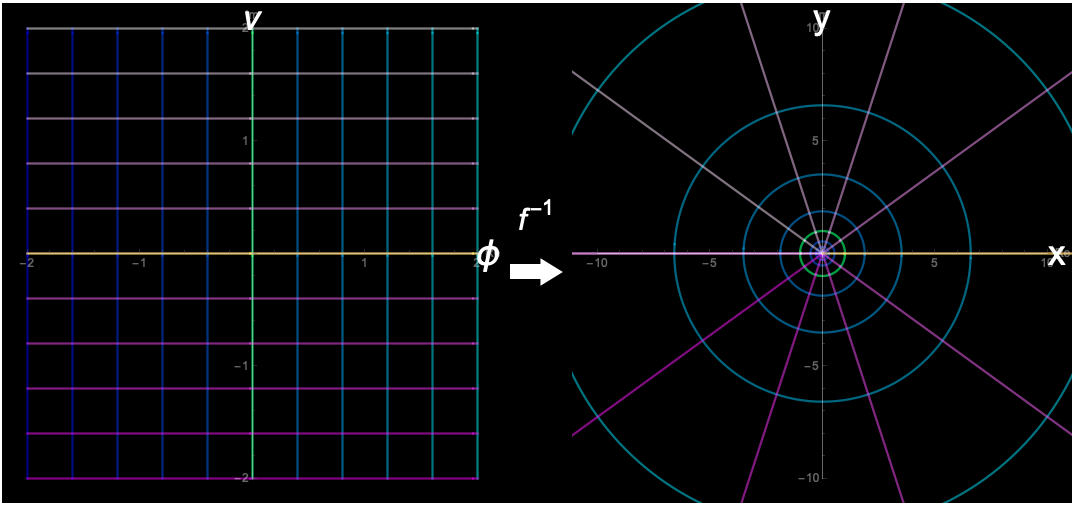
等電位面と電気力線

$\phi=\phi_0$を満たす曲線 $ (x(\phi_0,\nu),y(\phi_0,\nu))$は等電位面となります。また$\nu$が一定の曲線は電気力線となります。$\phi(x,y)$ という関数は位置$(x,y)$の電位の高さを求める関数になりますが、これから等電位面や電気力線のパラメータ表示を求めるには、逆関数を求める必要があります。
等電位面と電気力線

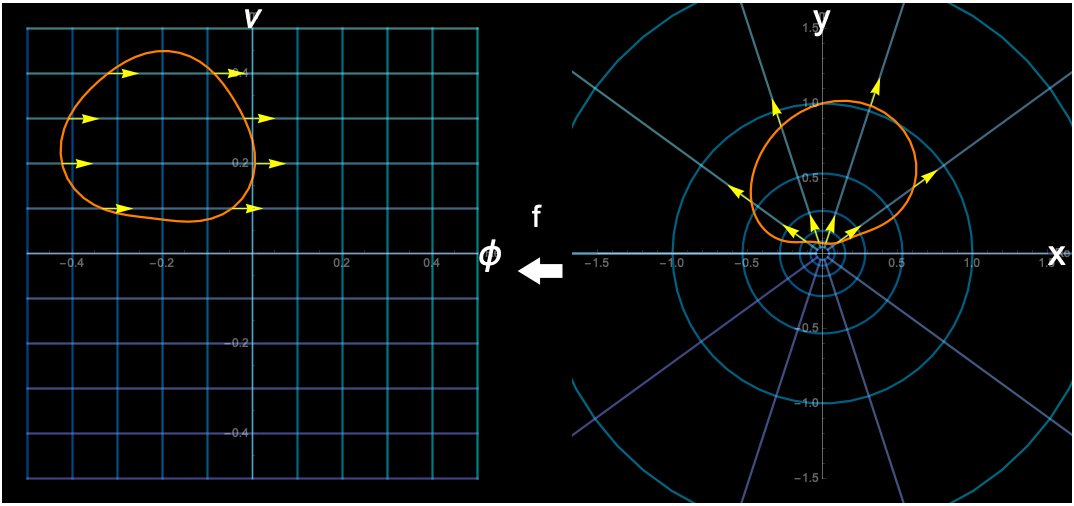
閉曲線から外に向かう電気力線を数える

$xy$平面上に閉曲線$C$を引き、$C$の内から外に向かう電気力線の数を数えます。カウントの際、外向きを$+1$、内向きを$-1$とします。電気力線の数は$\phi\nu$平面で$\nu$方向の長さになります。このため$\phi\nu$平面上の$C$の像の始点と終点の$\nu$の差が求めるものになります。これから$f$が閉曲線を閉曲線に移す場合、$C$から出ていく電気力線の総量はゼロになることがわかります。ゼロにならないためには、$f$は閉曲線を開く必要があります。複素関数でこのようなことが起こるのは、$C$の内部に分岐点があるときです。分岐点はその周りを一周しても像が元の位置に戻ってこないような点で、$w=\sqrt{z}$のような関数がもつ代数分岐点と、$w=\log{z}$が持つ対数分岐点があります。代数分岐点の場合$n$周したらカウントがゼロになってしまうので、電気力線の源としてふさわしいのは対数分岐点です。

電気力線の総量がゼロにならない場合
電気力線の総量がゼロになる場合
電気力線の間隔を1とすると$d\nu$に含まれる電気力線の数は$d\nu$です。$C$から出ていく電気力線の総量を$Q$とすると
$$ Q = \int_C d \nu $$
$xy$平面の式にするため$C$に沿った微小ベクトル$d \mathbf{x} = \begin{pmatrix} dx \\ dy \end{pmatrix}$で表すと
$$ Q = \int_C \nabla \nu \cdot d \mathbf{x} = \int_C (\nu_x dx + \nu_y dy ) $$
コーシー・リーマンの方程式、もしくは$\nu$の流線と$\phi$の流線が直行することから
$$ Q = \int_C (\phi_y dx - \phi_x dy ) $$
ここで$d \mathbf{x}$に直行するベクトルを$\mathbf{n} dl = \begin{pmatrix} dy \\ -dx \end{pmatrix}$とします。$C$にそった積分を右回りに行うとき、このベクトルは$C$の外側に向いたベクトルになります。これより求める積分は
$$ Q = \int_C (-\nabla \phi) \cdot \mathbf{n} dl = \int_C \mathbf{E} \cdot \mathbf{n} dl $$
と表せます。

発散とガウスの定理

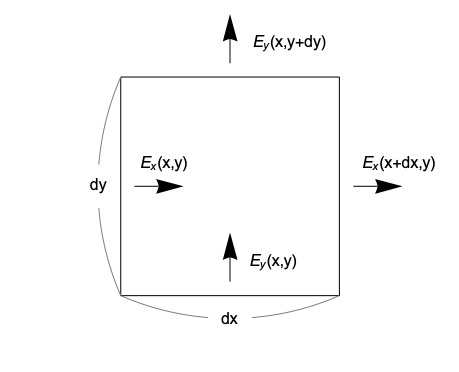微小正方形に対する積分
さきの積分を微小正方形について考えたものを$q$とすると、上図より
$$ q=(E_x(x+dx,y) - E_x(x,y))dy + (E_y(x,y+dy)-E_y(x,y))dx $$
これを微小正方形の面積$dxdy$で割ると
$$ \nabla \cdot \mathbf{E} = \frac{\partial E_x}{\partial x} + \frac{\partial E_y}{\partial y} $$
という量になり$\mathbf{E}$の発散とよびます。

この微小領域をAとし、隣接した微小領域をBとします。これらをつなげた領域について同じ計算をしたものを$q_{A+B}$、それぞれの領域についてを $q_A、q_B$とすると共通する線での打ち消し合いが起こるので$q_{A+B} = q_A + q_B$となります。
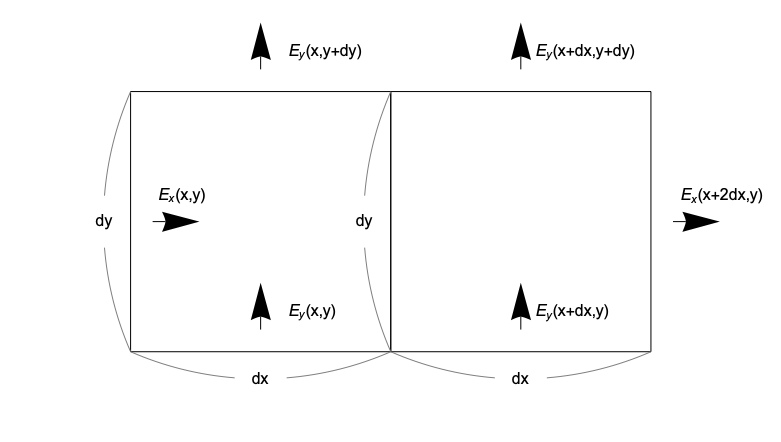２つの領域をつなげた場合
どのような領域でも微小正方形に分割して同じことが言えるので$C$の内部の領域を$S$として
$$ Q = \int_C \mathbf{E} \cdot \mathbf{n} dl = \int_S (\nabla \cdot \mathbf{E})dS $$
が成り立ちます。これをガウスの定理といいます。$\mathbf{E}=-\nabla \phi$なので
$$ Q = - \int_S (\nabla^2 \phi)dS $$
これから$S$の内部のすべてで$\nabla^2 \phi = 0$であれば、$Q=0$となります。

留数定理との関係

$Q$を複素数の演算だけで表すとどうなるでしょうか？
\begin{eqnarray} dw = f'(z) dz &=& \phi_x dx + \phi_y dy + i (\nu_x dx + \nu_y dy) \end{eqnarray}
また$Q = \int_C (\nu_x dx + \nu_y dy )$なので
$$ Q = \textrm{Im}\left[\int_C f'(z) dz\right] $$
よって$f'(z)$の経路積分の虚数成分が閉曲線からでてくる電気力線の数、すなわち閉曲線の中にある電荷の総量になります。電荷は$f'(z)$の極に対応し、$f(z)$においては$1/z$の積分である対数分岐点になります。電荷を複素数にして
$$ Q = \int_C (\phi_x dx + \phi_y dy ) + i \int_C (\nu_x dx + \nu_y dy ) $$
と定義すれば
$$ Q = \int_C f'(z) dz $$
となります。静電場では電位が循環することはないので、実数部分は常にゼロになります。ただしコイルの中で磁界が変化したときなどに生じる誘導電場は循環する電場とみなせるので、これを虚数の電荷として表現できるかもしれません。

具体例

というわけで複素関数は電場を表し、電場と電荷の関係はポアソン方程式で表されます。そしてこれは２次元のグリーン関数$\ln |\mathbf{x}-\mathbf{s}|/2\pi$の重ね合わせで求まります。なので位置$a$にある電荷$Q_a$の作る電場は
$$ w = (Q_a/2\pi) \ln (z-a) $$
という関数で表され、複数の電荷が作る電場は

\begin{eqnarray} w &=& (Q_a/2\pi) \ln (z-a) + (Q_b/2\pi) \ln (z-b) + (Q_c/2\pi) \ln (z-c) + ~.. \\ &=& (1/2\pi) \ln((z-a)^{Q_a}(z-b)^{Q_b}(z-c)^{Q_c} ~ ..) \end{eqnarray}
と表せます。

点電荷

点電荷が作る電場は$w = (1/2\pi) \ln z$です。よって$z = \exp(2 \pi w )$が電気力線を表します。
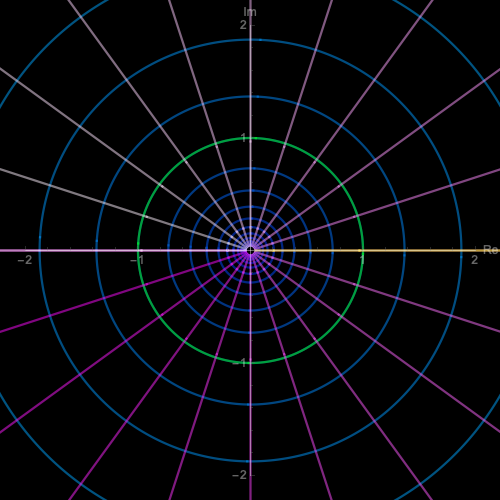点電荷

双極子

$z=1$と$z=-1$にある電荷を考えます。

同符号の電荷の場合

$w = (1/2\pi) \ln ((z-1)(z+1))$
$z = \sqrt{1+e^{2 \pi w}}$
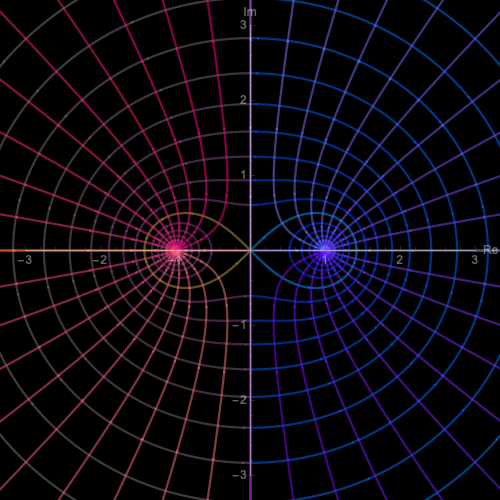双極子(同符号)
複素関数が多価になるときもプログラム言語の関数は必ず一つの値を返すので、他の分岐は手動で重ね書きする必要があります。この図では青線と赤線が異なる分岐に対応します。

異符号の電荷の場合

$w = (1/2\pi) \ln ((z-1)/(z+1))$
$z = \coth(\pi w)$
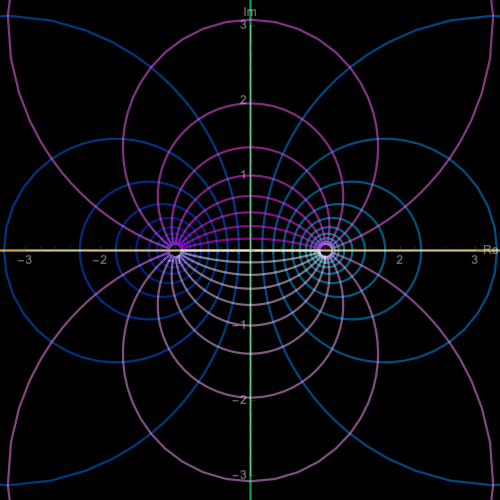双極子(異符号)

複数の電荷

円周上にならんだ電荷

$w = (1/2\pi) \ln (z^n -1)$
$z = -(1+e^{2 \pi w})^{1/n}$
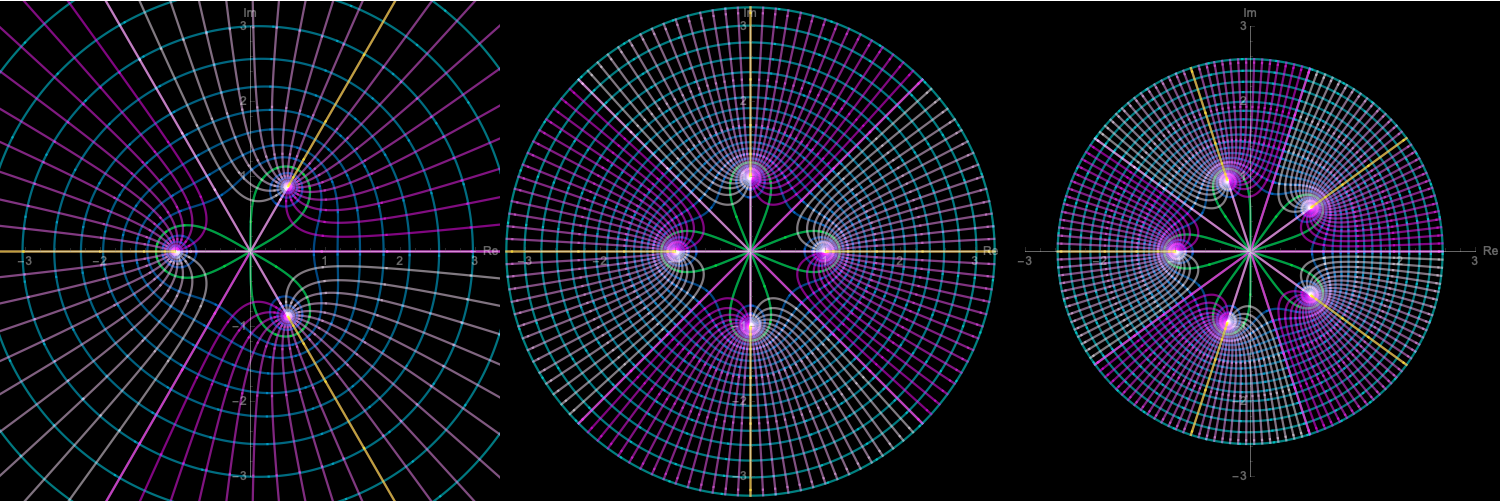円周上にならんだ電荷

四重極電荷

$$ w = (1/2\pi) \ln \frac{z^2-1}{z^2+1} $$
$$ z = \sqrt{\frac{1+e^{2 \pi w}}{1-e^{2 \pi w}}} $$
四重極電荷

対称性が少ない場合

逆関数が求まるのは電荷の比や空間的な配置に対称性があるときで、対称性が少なくなるととたんに解けなくなります。ここではギリギリ解けたケースを紹介します。

1:2の比の異符号の電荷

$$ w = (1/2\pi) \ln (z(z-1)^{-1/2}) $$
$$ z = \frac{e^{2 \pi w}}{2} \left(e^{2 \pi w} + i \sqrt{4-e^{4\pi w}} \right) $$
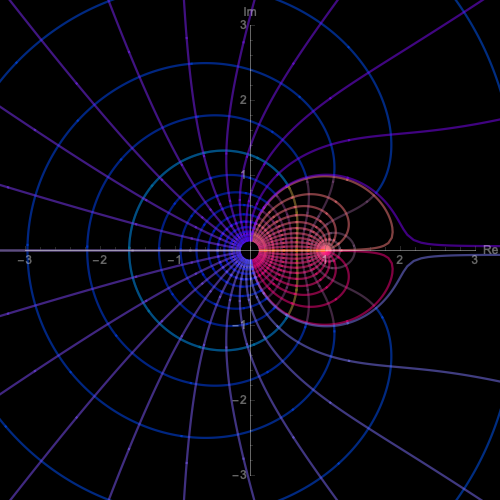1:2の比の電荷（異符号）

1:2の比の同符号の電荷

$$ w = (1/2\pi) \ln (z(z-1)^{1/2}) $$
$$ z = \frac{1}{3} \left(1 + \left(\frac{2}{2 + 27 e^{4\pi w} + 3 \sqrt{3} + e^{2 \pi w} \sqrt{4 + 27 e^{4 \pi w}}}\right)^{1/3} + \left(\frac{2}{2 + 27 e^{4\pi w} + 3 \sqrt{3} + e^{2 \pi w} \sqrt{4 + 27 e^{4 \pi w}}}\right)^{-1/3} \right) $$
1:2の比の電荷（同符号）

３つ並んだ電荷

$$ w = (1/2\pi) \ln (z(z^2-1)) $$
$$ z = \frac{1}{3} \left(\frac{27 e^{2 \pi w} + \sqrt{-4 \cdot 27 + (27 e^{2 \pi w})^2}}{2}\right)^{1/3} + \left(\frac{27 e^{2 \pi w} + \sqrt{-4 \cdot 27 + (27 e^{2 \pi w})^2}}{2}\right)^{-1/3} $$
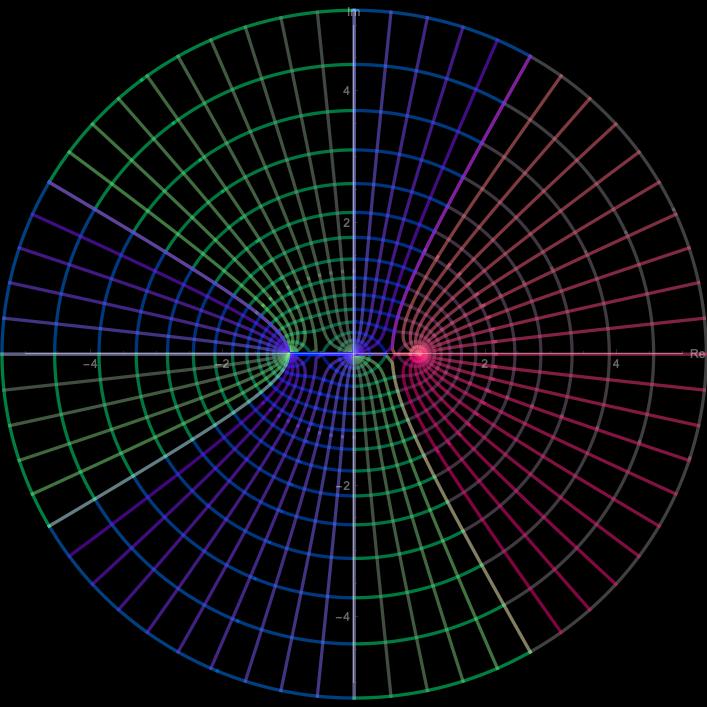３つ並んだ電荷
このように不自然な分岐の取り方になっています。冪根を含んだ式について自然な分岐の取り方をどう決めればいいのか？というのも研究テーマになりそうです。

一様電場

一様電場は$w=z$となりますが、これを電荷の作る電場として解釈してみます。$w=\ln(e^z)$であり、また$e^z = \lim_{n\to\infty} (1+x/n)^n$であることから、一様電場は無限遠にある無限の電荷とみなせます。

一様電場中の点電荷

$$ w = z + (1/2\pi) \ln (z-1) $$
$$ z = 1 + W(e^{-1+w}) $$
ここで$W$はランベルトの$W$関数です。
一様電場中の点電荷

解釈が知られている関数

境界条件が具体的な問題と一致する関数というのが知られています。

一様電場中の円筒導体

$$ z = w + 1/w $$
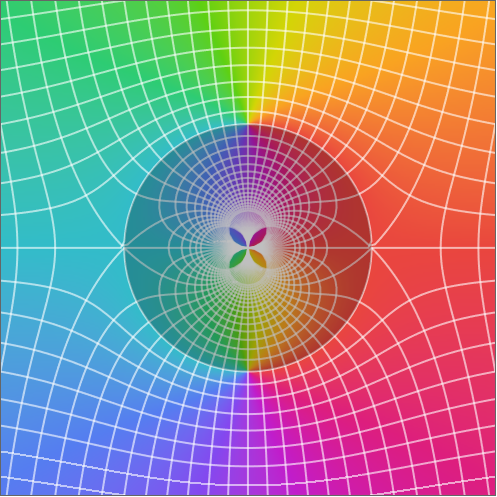一様電場中の円筒導体

直角に接続された金属板

$$ z = w^{1/2} $$
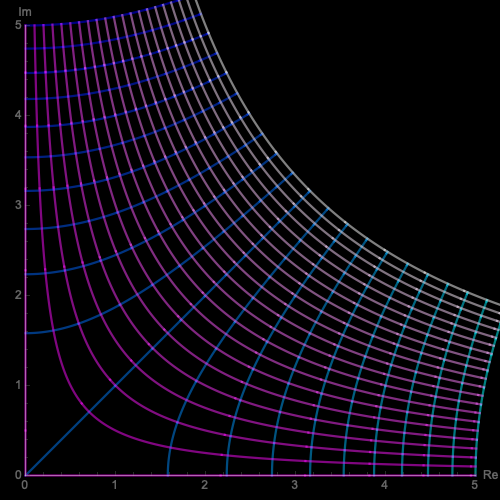直角に接続された金属板

任意の曲線形状の金属板

曲線がパラメータ表示$(x(t),y(t))$をもつとき、$z=x(w)+i y(w)$という複素関数はその曲線にそった等電位面を表します。例えば$x(t) = t, y(t) = \sin(t)$だと下図のようになります。
$z = w + i \sin(w)$
これを無限遠まで続けると等電位面が重なってしまうところがでてきて解釈が破綻してしまいますが、近傍では任意の曲線形状の金属板が作る電場になっているのではないかと思います。

ありがとうございました。