二項係数Part3 〜整数係数多項式による整数の分類〜
はじめに
この記事は、二項係数の連載のPart3です。 Part1 , Part2 を読んでいない方は、ぜひ先にご覧ください。
テーマ
今回は、二項係数からは外れますが、「整数係数多項式による整数の分類」というものについて書いていきます。整数係数多項式$f(x)$が与えられたとき、$f(x)\mod p$が等しい$x$を同値とみなす同値類を考えるということです。
整数係数多項式による整数の分類
以下、$p$を素数とします。整数係数多項式$f(x)$が与えられると、
$$R(i;p)=\{x\in \mathbb{Z}|f(x)\equiv i\mod p\}$$
として、
$$
\mathbb{Z}=\bigcup_{i = 0}^{p-1}R(i;p)
$$
と、$\mathbb{Z}$を互いに交わらない$p$個の集合に分けることができます。さらに、
$$
f(x)\equiv i\mod p^e \Leftrightarrow f(x)\equiv i,i+p^e,\cdots ,i+(p-1)p^e \mod p^{e+1}
$$
であるので、
$$
R(i;p^e)=\bigcup_{k=0}^{p-1}R(i+kp;p^{e+1})
$$
と、$R(i;p^e)$をさらに互いに交わらない$p$個の集合に分けることができます。このような分類を次のような図で捉えます。
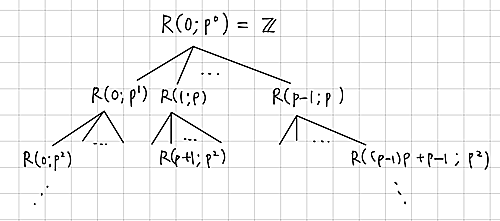 分類
分類
一番上を$0$段目として数えることにします。また、各$R(i;p^e)$を部屋と考え、「$e$段目の$i$号室」などと表すことにします。
さて、例えば$1$段目では、$1$と$p+1$を区別する必要はありません。そこで、次のような比喩を考えたいと思います。すなわち、$0$段目から$0,1,\cdots ,p-1$が落ちてきて、$1$段目の然るべき部屋に入ります。$1$は$1,p+1,\cdots ,(p-1)p+1$の$p$個に分裂して$2$段目の然るべき部屋に入り、他の数も同様にして、無限に下の方に落ちてゆくのです。
このとき、各数の落ち方には規則があるのです。その規則を知ることで、与えられた$x\in \mathbb{Z}$に対して、$x$がどの部屋に入るのか、すなわち$f(x)\mod p^e$を求められる場合があるということです。その最も重要な規則は次のものです。
$x\in \{0,1,\cdots ,p-1\}$に対し、$f'(x)\not\equiv 0\mod p$ならば、$x$が分裂してできた$p$個は一段下の$p$個の部屋に一つずつバラバラに落ちる。以降$x$を先祖に持つものはすべて同じ落ち方をする。
一方、$f'(x)\equiv 0\mod p$ならば、$x$が分裂してできた$p$個は一段下の$p$個の部屋のいずれか一つにまとまって落ちる。以降$x$を先祖に持つものはすべて同じ落ち方をする。
つまり、$f(x)\mod p^e$について知りたかったら、$f'(x)\mod p$が$0$か否かを調べるとよいわけです。それがいわば$x$の遺伝子であり、$0$でないなら常にバラバラに落ちてきたこと、$0$なら常にまとまって落ちてきたことが分かるのです。
これは整数論の初等的な定理であり、特に難しい証明は要しませんが、きちんと書くと長くなりますし、本記事の趣旨から外れますので、証明は省きます。
例
例として、次の問題を考えてみましょう。
$p$を奇素数とする。$x^{p-1}\equiv k\mod p^e\ (0\leq x \leq p^e-1)$の解の個数を調べよ。
(解答)
フェルマーの小定理より、$e=1$のときは自明($k=0$のとき1個,$k=1$のとき$p-1$個,他$0$個)。$e>1$のときを考える。$f(x)=x^{p-1}$とすると、$f'(x)=(p-1)x^{p-2}$であり、これが$p$を法として$0$となるのは$x=0$のみだから、$1,2,\cdots ,p-1$は以降常にバラバラに落ち、$0$は以降常にまとまって落ちる。したがって、解の個数は、$k\equiv 1\mod p$のとき$p-1$個、$k\equiv 0\mod p$のとき$p^{e-1}$個である。その他の場合は$0$個である。
$(x-3)^2\equiv 0\mod 49$を満たす$0\leq x \leq 48$をすべて求めよ。
(解答)
$(x-3)^2\equiv 0\mod 7$の解は$x=3$のみ。$f(x)=(x-3)^2$として、$f'(3)\equiv 0\mod 7$なので、$3$は$3,10,\cdots ,45$の$7$個に分裂して一つの部屋にまとまって落ちる。$f(3)\equiv 0\mod 49$より、これらはすべて$0$号室に落ちたと分かるから、求める解は$3,10,\cdots ,45$である。
おわりに
今回の分類法を用いて、次回の記事で、いよいよ特殊な二項係数の素数のべきで割った余りを求める方法を紹介したいと思います。連載はそれで終わる予定です。
読んでいただきありがとうございました。
