Mathias強制法入門
Mathematical Logic Advent Calendar 2020 の21日目の記事です．
この記事ではMathias強制法の初歩の解説を行う．
Mathias強制法の定義
$$
\M = \{ (s, A) : s \in [\omega]^{<\omega} \and A \in [\omega]^\omega \and \max s < \min A \}
$$
で$\M$の元の間の順序は
$$
(t, B) \le (s, A) \iff (s \subseteq t) \and (B \subseteq A) \and (t \setminus s \subseteq A)
$$
で定める．
$\M$をMathias強制法という．
$\M$の最大元は$(\varnothing, \omega)$でありこれを$1_\M$と書く．
Mathias強制法は$\omega$のある部分集合$g$ (Mathias実数という)を追加する強制法であり，各条件 ($\M$の元)はその追加する実数の近似と思える．
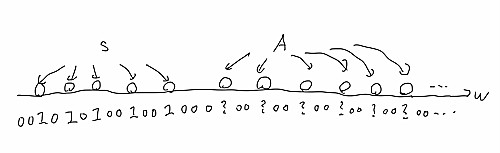mathias
まず，$s$の元は$g$に入れる．$s$にも$A$にも入っていない自然数は$g$に入れない．$A$に入っている自然数は$g$に入れるかどうかは未定である．
このことをフォーマルに述べると次の通りだ．
$(V, \M)$ジェネリックフィルター$G$に対して$g = \bigcup \{ s : (\exists A)((s, A) \in G) \} \subseteq \omega$とおく．$g$をMathias実数という．$g$を表す名前を$\dot{g} \in V^\M$とする．
このとき，$(s, A) \in \M$に対して
$$
(s, A) \forces_\M s \subseteq \dot{g} \subseteq s \cup A.
$$
$(s, A) \in \M$を含む$(V, \M)$ジェネリックフィルター$G$をとる．
このとき，$g$の定義から$s \subseteq g$である．
また，$n \in g$とすると$(t, B) \in G$があって$n \in t$である．$G$はフィルタ―なので$(u, C) \le (s, A), (t, B)$をとれる．$\M$の順序の定義より$t \subseteq u$なので$n \in u$でもある．$n \in s$ならば$n \in s \cup A$となる．$n \not \in s$ならば$\M$の順序の定義より$n \in u \setminus s \subseteq A$なので$n \in s \cup A$である．よって，どちらにせよ$n \in s \cup A$.
したがって強制定理により命題の主張を得る．
Mathias強制法はcccを満たさないが，Axiom Aという性質を満たし，したがってproperという性質を満たすことを注意しておく．
Mathias強制法はsplitting numberを上げる
$x, y \in [\omega]^\omega$について$x$が$y$をsplitするとは$y \cap x$と$y \setminus x$がともに無限なことと定める．
Mathias実数はグラウンドモデルのどんな実数によってもsplitされない．すなわち次が成り立つ．
$1_\M \forces_\M (\forall x \in \mathcal{P}(\omega) \cap V)(|\dot{g} \cap x| < \aleph_0 \or |\dot{g} \setminus x| < \aleph_0)$
$V$で議論する．$(s, A) \in M$とし，$x \in \mathcal{P}(\omega)$とする．
$A$が無限集合なので$A \cap x$と$A \setminus x$の少なくともどちらかは無限である．
$A \cap x$が無限ならば，$(s, A\cap x) \forces_\M (\dot{g} \subseteq s \cup (A \cap x))$であるので，$(s, A\cap x) \forces_\M (\dot{g} \setminus x \subseteq (s \cup (A \cap x)) \setminus x \subseteq s)$で$s$は有限集合なので$(s, A\cap x) \forces_\M (|\dot{g} \setminus x| < \aleph_0)$.
$A \setminus x$が無限ならば，同様に$(s, A\setminus x) \forces_\M (|\dot{g} \cap x| < \aleph_0)$となる．
$\mathcal{F} \subseteq [\omega]^\omega$がsplitting familyであるとは，どんな$Y \in [\omega]^\omega$もある$X \in \mathcal{F}$によってsplitされることをいう．
$$
\mathfrak{s} = \min\{|\mathcal{F}| : \text{$\mathcal{F} \subseteq [\omega]^\omega$はsplitting family} \}
$$
とおき，$\mathfrak{s}$をsplitting numberという．
次は反復強制法やproper強制の性質を使うが，証明の概略は明快なので概略を述べる．
CHを仮定する．順序数$\alpha$について$\P_\alpha$をMathias強制法の$\alpha$回の可算サポート反復とする．このとき
$$
\P_{\omega_2} \forces \mathfrak{s} = 2^{\aleph_0} = \aleph_2.
$$
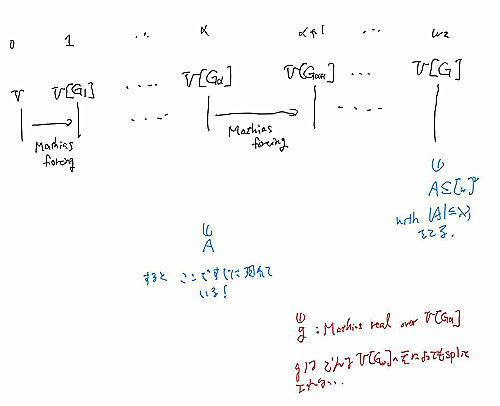iteration
$(V, \P_{\omega_2})$ジェネリックフィルター$G$をとる．$V[G]$の中で$A \subseteq [\omega]^\omega$を$|A| \le \omega_1$を満たすものとする．
CHの仮定と$\M$がサイズ連続体濃度のproper強制法なことから，proper強制法の性質により，$A$は途中のステージ$V[G_\alpha]$ (ただし$\alpha < \omega_2$)で現れ，また$V[G]$で$2^{\aleph_0} = \aleph_2$である．
$V[G_\alpha]$から$V[G_{\alpha+1}]$へ行くときに追加されるMathias実数$g$を考える．このとき命題2より$V[G_{\alpha+1}]$の中で，どんな$x \in A$も$g$をsplitしないことが分かる．二つの実数$X, Y$について「$X$が$Y$をsplitする」という関係は絶対的であるので，同じことが$V[G]$でも成り立つ．したがって，$V[G]$の中で$A$はsplitting familyではない．
$A$は濃度$\aleph_1$以下で任意にとっていたことから，$\mathfrak{s} > \aleph_1$である．よって$2^{\aleph_0} = \aleph_2$より$\mathfrak{s} = \aleph_2$である．
ほかの性質
- Mathias強制法はdominating realを追加し，したがって$\mathfrak{b}$を上げる
- Mathias強制法はLaverの性質を持ち，したがって$\cov(\nll)$と$\cov(\meager)$を小さくする
- $V^{\P_{\omega_2}}$ではBorel予想が成り立つ．
1はそれほど証明は難しくない．2の証明にはMathias forcingが"pure decision"という性質を持つことを使い，ちょっと議論が必要だ．3はさらに議論が必要．
余力があれば1と2についてこの記事に証明を追記したいと思う．特にpure decisionはMathias強制の最も重要な性質の一つなので書いておきたい思いはある．
今回書いた$\mathfrak{s}$を上げるという事実と項目1と2により結局，Mathias強制法の$\omega_2$回反復で次のような基数不変量の分離ができる．オレンジが$\aleph_2$になる部分，水色が$\aleph_1$になる部分である．薄いオレンジは$\aleph_2$になるが，この記事では証明しない部分である．
invariants
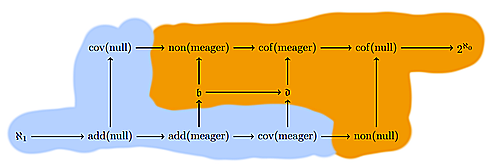cichon
ただし1枚目の画像は参考文献1の図に色を付けたものである．
ZFCで証明できる不等式$\mathfrak{s} \le \non(\nll)$があることに注意しておく．よって$\mathfrak{s}$が上がることから$\non(\nll)$も上がる．また，$\mathfrak{e} \le \cov(\meager)$という不等式もあるので，$\cov(\meager)$が下がることから$\mathfrak{e}$も下がる．
実は$\P_{\omega_2}$が薄いオレンジの部分を上げることは既に証明を記事にしてある:
参考文献
- Blass A. (2010) Combinatorial Cardinal Characteristics of the Continuum. In: Foreman M., Kanamori A. (eds) Handbook of Set Theory. Springer, Dordrecht. https://doi.org/10.1007/978-1-4020-5764-9_7
