コンウェイが遺した最もキャッチーなモーリーの定理の証明

図形,モーリーの定理,コンウェイ

4057

はじめに

モーリーの奇跡とも呼ばれるフランク・モーリーの定理．数多くの証明が知られ未だに新たなものが生み出される「最も美しい初等幾何の定理」の主張をまずは見てみましょう．

Morley 1899

三角形の各内角の三等分線どうしが最初に出会う点は正三角形をなす．
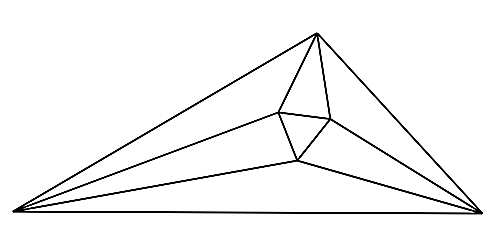trisector1

モーリー自身もこれほど目を惹く結果が2000年以上見過ごされてきたとは信じられず，新規の成果として正式に発表するのは遅れたようです(1924?)．やはり，角の三等分線が作図不可能であることからなかなか先人たちの考察が及んでいなかったということなのでしょうか．もしかしたら，発見していても同じように発表を躊躇した人がいたかもしれません．

本記事では，ジョン・コンウェイによる視覚的で呆気にとられてしまうような証明を紹介します．記憶に新しいかと思いますが，偉大な数学者である彼は2020年4月にCOVID-19が原因で亡くなられました．改めて哀悼の意を表します．

コンウェイによる証明

$A = 3 α, B = 3 β, C = 3 γ$ $(α + β + γ = 60^{\circ})$ なる三角形 $A B C$ が与えられたとします．これに対して，以下のような $7$ つのピースを用意します．
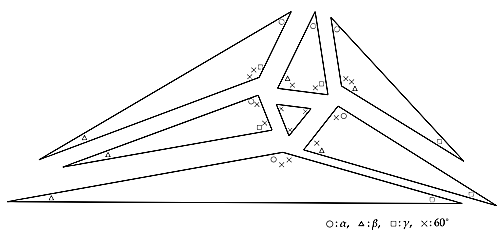trisector2
そして，外側の $3$ つのピースには補助線を次のように引きます．
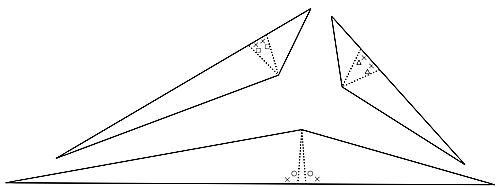trisector3

今，下図における赤い部分の長さがいずれも等しくなるように各ピースを拡大縮小します．すると，これらはジグソーパズルのようにかっちりと組みあがるのです．確認してみましょう．
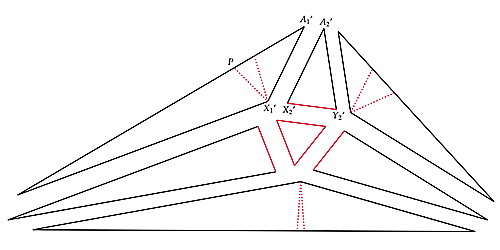trisector4
中央にある正三角形の各頂点まわりの角度の和が $360^{\circ}$ となって整合することはすぐにわかります．長さについてはどうでしょうか．ここで補助線が活きてきます．例えば， $△ A_{1}^{'} X_{1}^{'} P$ と $△ A_{2}^{'} X_{2}^{'} Y_{2}^{'}$ に着目すると対応する頂角の大きさが等しく $X_{1}^{'} P = X_{2}^{'} Y_{2}^{'}$ なので合同であり，特に $A_{1}^{'} X_{1}^{'} = A_{2}^{'} X_{2}^{'}$ となります．他の接着する辺のペアについても同様です．
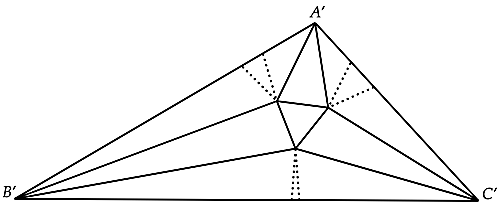
こうしてできた $A^{'} = 3 α, B^{'} = 3 β, C^{'} = 3 γ$ $(α + β + γ = 60^{\circ})$ なる三角形 $A^{'} B^{'} C^{'}$ は内角の三等分線の交点によって正三角形が作られています．また，適当な拡大縮小によって $A^{'} B^{'} C^{'}$ は $A B C$ と合同になります．
trisector5
ところで，各内角の三等分線の引き方はただ一通りしかありません．よって $A B C$ の各内角の三等分線どうしが最初に出会う点は正三角形をなすことが示されました．

おわりに

気づかれましたか?実は筆者のアイコンはこの定理が成立する様を表しています．そのくらいお気に入りです．中学生のときに難波誠「平面図形の幾何学」(現代数学社)の中で出会い，定理内容のわかりやすさと美しさ，そして何よりも19世紀末になってようやく発見されたということに衝撃を受けました．これがきっかけで本格的な数学の虜になったと言っても過言ではありません．これはもう実質的な自己紹介記事です．

追記：複素座標を用いた証明も書きました．