おまけ：複素座標の練習としてのモーリーの定理
前回は コンウェイによるモーリーの定理の証明 をお話ししました．natuさんという方がせっかく 複素座標入門 にて整備してくださっているので，それを用いた方法も載せておきます．素朴な計算による証明はかえって置いてないんですよね．
複素座標を用いた証明
単位円を外接円にもち各頂点が
$$A(a^3),B(b^3),C(c^3) (|a|=|b|=|c|=1,\ 0 \leq\arg{a}<\arg{b}<\arg{c}< \frac{2}{3}\pi)$$
と表される三角形$ABC$に対して示せば十分．以降，見やすさのため$\omega=\cos {\frac{2}{3}\pi} +i\sin{\frac{2}{3}\pi}$とおく．
すると，各内角の三等分線と外接円との交点の座標は以下のように求まる．
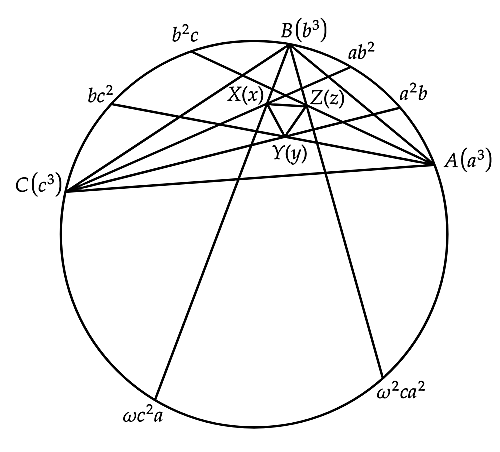diagram1
$a^3,bc^2$を通る弦と$b^3, \omega c^2a$を通る弦の交点$X$は
$$
\begin{eqnarray}
\left\{
\begin{array}{l}
x+ab^2c^3\bar{x}=ab^2+c^3 \\
x+\omega ab^3c^2\bar{x}=\omega ac^2+b^3
\end{array}
\right.
\end{eqnarray}
$$
を満たす．辺々を引いて整理すると
$$
a^2b^2c^2 \bar{x}=\omega^2(ab^2-a^2b)-\omega(ca^2-\omega^2c^2a)+\omega abc
$$
を得る．$Y,Z$に対しても同様にして
$$
a^2b^2c^2\bar{y}=(bc^2-b^2c)-(ab^2-a^2b)+abc\\
a^2b^2c^2\bar{z}=(ca^2-\omega^2c^2a)-\omega(bc^2-b^2c)+\omega^2abc
$$
よって$\bar{x}+\omega^2\bar{y}+\omega\bar{z}=0$すなわち
$$
x+\omega y+\omega^2 z=0
$$
これは$X,Y,Z$が正三角形をなすことを意味する．$\blacksquare $
