テンソル積の存在と一意性(と自己紹介)
こんにちは!るめなるです!この記事では,私の自己紹介,またテンソル積の存在とその一意性について書きたいと思います.
自己紹介
15歳(中3)の数学好きです.特に数論分野の類体論と,$p$進に興味があります.また,息抜きとして積分と級数をしていて,Twitterに自作問題を載せたりしています.最近積分を解くためによく使われる技法や公式,特殊関数などについてまとめたpdfを書いたので見ていただけると嬉しいです!(Twitterのプロフィールの固定ツイートにあります.)
テンソル積
今回は,練習も兼ねてテンソル積の存在,一意性について書いてみようと思います.ただ,簡単のために今回は可換環上の加群について考えることにします.少しおかしい部分や誤植などがあればコメントいただけると喜びます.
まずは主張を書いておきます.
$A$を可換環,$M$,$N$を$A$加群とする.このとき,次の性質(テンソル積の普遍性という)をもつ$A$加群$T$と$A$双線形写像$\phi:M \times N \to T$が存在する.
性質
任意の$A$加群$S$と任意の$A$双線形写像$f:M \times N \to S$に対して,$f = g \circ \phi$を満たすただひとつの$A$線形写像$g:T \to S$が存在する.
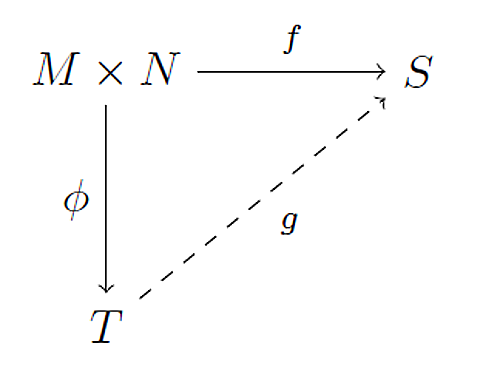 図式1
図式1
それでは,この定理を証明していきましょう.概略としては,良い性質を満たすように$A$加群$T$と$A$双線形写像$\phi$を構成し,最後にテンソル積の普遍性を示すという流れになります.
Step1. $T$の土台となる加群の定義
$F$を自由$A$加群$\displaystyle \bigoplus_{M \times N} A$,すなわち$F$を$A$を係数とする$M \times N$の形式的な有限和$\displaystyle \sum_{i=1}^{n} a_i (x_i, y_i)~~(a_i \in A,~x_i \in M,~y_i \in N)$のなす$A$加群とする.
Step2. $T$の構成
$G$を次のような形の$F$のすべての元によって生成される$F$の部分加群とする.
- $(x+x',y) - (x,y) - (x',y)$
- $(x,y+y') - (x,y) - (x,y')$
- $(ax,y) - a \cdot (x,y)$
- $(x,ay) - a \cdot (x,y)$
ここで,$T = F/G$とおく.勘のいい読者の方はお気づきだろうが,このように$G$を定義し,$T$を$F/G$と定義することで,$A$双線形写像$\phi$をうまく構成できるのである.
Step3.$\phi$の構成
$F$から$T=F/G$への自然な全射$A$準同型を$\pi$とし,$F$の基底をなす任意の元$(x,y)$に対して$\pi(x,y)$を$x \otimes y$とかく.このとき,$\pi$が全射であることから$T$は$x \otimes y$という形の元により生成される.また,$G$の定義より,
- $(x+x') \otimes y = x \otimes y + x' \otimes y$
- $x \otimes (y + y') = x \otimes y + x \otimes y'$
- $(ax) \otimes y = x \otimes (ay) = a(x \otimes y)$
が成り立つ.ここで写像$\phi$を$\phi(x,y)=x\otimes y$と定義すると,上3つの性質は$\phi$が$A$双線形写像であることの条件に他ならない(これがStep2の最後に述べたことの意味である).したがって写像$\phi:M \times N \to T$は$A$双線形写像となる.
Step4. $T$と$\phi$がテンソル積の普遍性を満たすこと
与えられた$f:M \times N \to S$は線形であるから,$f$は$A$準同型写像$\bar{f}:F \to S$に拡張できる.$G$の定義とそれから導かれるStep3に挙げた3つの性質より,$\bar{f}(G)=\{0\}$.したがって,準同型定理(注意参照)により$\phi(x \otimes y) = f(x,y)$を満たすwell-definedな$A$準同型写像$\phi: T \to S$が誘導される.また,$\phi$はこの条件$\phi(x \otimes y) = f(x,y)$によって一意に定まる.以上より,$T$と$\phi$がテンソル積の普遍性を満たすことが分かった.
上の証明のStep4における準同型定理は,
準同型定理
$M$,$N$を$A$加群,$L \subset M$を部分$A$加群,$f:M \to N$を$A$準同型写像,$\pi: M \to M/L$を自然な$A$準同型とするとき,準同型$g:M/L \to N$で$f=g \circ \pi$となるものが存在することと,$L \subset \textrm{Ker}(f)$であることは同値.
というものである.
次に,非常に重要なテンソル積の一意性を示します.これは$M$,$N$に対してテンソル積の普遍性を満たすような加群と$A$双線形写像が複数あった場合,それらの加群はすべて同型で,双線形写像も同じものとみなせるという定理です.すなわち,テンソル積が普遍性によって特徴づけられているということを意味するのです.
$A$を可換環,$M$,$N$を$A$加群とし,$(T,\phi)$,$(T', \phi')$をテンソル積の普遍性を満たす2つの組とする.このとき,$i \circ \phi = \phi'$を満たすただひとつの$A$同型写像$i:T \to T'$が存在する.
Step1.
テンソル積の普遍性より,ただひとつの$A$線形写像$i:T \to T'$と$i': T' \to T$が存在して,次の2つの図式が可換.すなわち,左で$\phi' = i \circ \phi$,右で$\phi = i' \circ \phi'$が成り立つ.
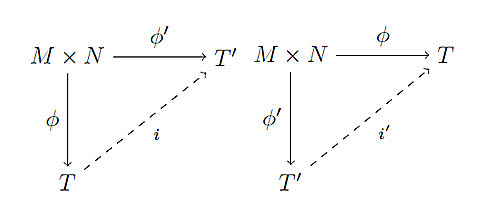 図式2
図式2
Step2.
Step1で得た図式を組み合わせれば,さらに次の2つの図式が可換となる.すなわち,左で$\phi = i' \circ i \circ \phi$,右で$\phi' = i \circ i' \circ \phi'$が成り立つ.
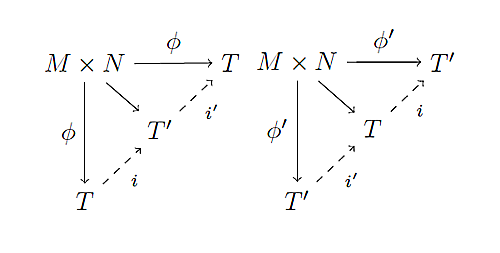 図式3
図式3
Step3.
ここで,明らかに次の2つの図式は可換である,($\phi = \textrm{id}_{T} \circ \phi$,$\phi' = \textrm{id}_{T'} \circ \phi'$が成り立つ)
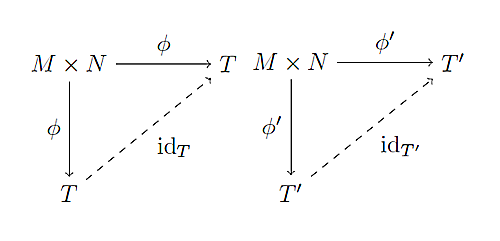 図式4
図式4
したがって,テンソル積の普遍性とStep2の図式より$i' \circ i = \textrm{id}_T$,$i \circ i' = \textrm{id}_{T'}$が成り立つが,これは$A$線形写像$i$の逆写像が$i'$であること,すなわち$A$線形写像$i:T \to T'$が$A$同型写像であることを意味する. ゆえに一意性が示された.
これで,ついにテンソル積の存在と一意性の両方を示すことができました.ところで,テンソル積の一意性の証明を振り返ってみると,登場する加群$M,N,T,T'$の内在的性質を全く使っていないことがわかるでしょう.使用したのは普遍性や写像の性質だけです.つまり,この証明は対象同士の相互関係のようなもののみを使っているといえます.
最近,Twitterなどで「圏論」という言葉を聞く人も多いのではないでしょうか.実は,この圏論ではこのように内在的性質をほとんど考えず,対象間の写像のようなもの(射とよばれる)を主に考察するのです.この話に興味がある方は龍孫江さんの次の記事も読むとさらによく分かると思います.
普遍性〜それは何であるべきか〜
今回はここまでにします.今後どのような記事を書いていくかは分かりませんが,恐らく私が勉強したこと(定理など)をまとめたり,Twitterに投稿した問題の解説を書いたりすると思います.ここまで読んでくださりありがとうございました!
