微分するとx軸方向に平行移動する実関数(f'(x)=f(x-t))を考えたら、想像以上にいっぱいあった件

いろいろと考えたのですが、自分には一般解を求めることができませんでした。
以前に投稿した$f'(x)=f(-x)$の問題 と同様、WolframAlphaが解いてくれない系の問題ですし、どうしようもない感が半端ないです・・・

わかる範囲($f(x)$が解析的と仮定する)で書いています。

$f(x)=e^{sx}$の形の解を見つける

$t=0$のときは$f'(x)=f(x)$なので、
$f(x)=Ce^x\ (C:任意定数)$であることは簡単にわかります。

$t\ne 0$の場合を考えます。
例えば$f(x)=e^{2x}$とすると$f'(x)=2e^{2x}$ですが、
変形すると$2e^{2x}=e^{2x+\log(2)}=e^{2(x+\frac{\log(2)}{2})}$なので、
$f'(x)=f(x+\frac{\log(2)}{2})$を満たします。
$t\ne 0$のときでも指数関数の形が解になりそうです。

$f(x)=e^{sx}\ (s>0)$とすると、
$f'(x)=se^{sx}=e^{sx+\log(s)}=e^{s(x+\frac{\log(s)}{s})}=f(x+\frac{\log(s)}{s})$なので、
$t=-\frac{\log(s)}{s}$となる$s$を求めればいいことが分かります。

ただ、この$s$は初等関数で求めることができなくて、「乗積対数関数」とか「ランベルトの$W$関数」などと呼ばれる関数$W(x)$を使って表します。
$W(x)$は、$y=xe^x$の逆関数です。
$t=-\frac{\log(s)}{s}$を変形すると$se^{st}=1$となりますが、
両辺に$t$を掛けて$ste^{st}=t$として、両辺に$W$関数をとると、
$st=W(t)$、すなわち$s=\frac{W(t)}{t}$であることがわかります。

したがって、$e^{\frac{W(t)}{t}x}$は$f'(x)=f(x-t)$を満たします。
さらに、実数倍した$Ce^{\frac{W(t)}{t}x}\ (C:任意定数)$もまた$f'(x)=f(x-t)$になります。

ただし、$W$関数には気を付けないといけないことがあります。
$W(x)$は実数の値域で$2$種類あるのです。

$W(x)$は「$1$つ」じゃない

$W(x)$は、$y=xe^x$の逆関数として導入しましたが、関数の逆関数が存在するためには、その関数が定義域から値域まで、1対1の対応をしていなければなりません。$y=xe^x$はグラフを描けばわかりますが、1対1の対応をしていません。

$y=xe^x$の増減表
$\begin{array}{|ccccc|} \hline x & -\infty & \cdots & -1 & \cdots \\ \hline y' & (0) & - & 0 & + \\ \hline y & (0) & \searrow & -\frac{1}{e} & \nearrow \\ \hline \end{array}$

$f(x)=xe^x$と$W$関数のグラフ

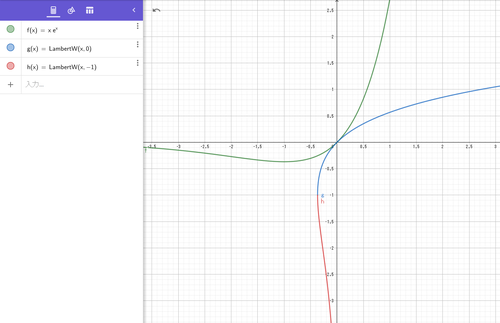xe^xとW関数

$y=xe^x$の定義域を適切に制限すれば逆関数を定義できるのですが、制限の仕方によって逆関数が変わります。
$y=xe^x\ (x\geqq-1)$の逆関数を$W_{0}(x)$、$y=xe^x\ (x\leqq-1)$の逆関数を$W_{-1}(x)$と書くことにします。

$W_{0}(x)$は定義域$x\geqq-\frac{1}{e}$、値域は$W_{0}(x)\geqq-1$、単調増加で原点を通る曲線です。
$W_{-1}(x)$は定義域$-\frac{1}{e}\leqq x<0$、値域は$W_{-1}(x)\leqq-1$、$x=0$を漸近線とする単調減少の曲線です。
$-\frac{1}{e}< x<0$の部分だけ$W(x)$が$2$種類あるんですね。

$f'(x)=f(x-t)$の問題に話を戻します。
$t>0$のとき、$Ce^{\frac{W_{0}(t)}{t}x}\ (C:任意定数)$が解になります。
$-\frac{1}{e}\leqq t<0$のときは、$e^{\frac{W_{0}(t)}{t}x}$も$e^{\frac{W_{-1}(t)}{t}x}$も解となります。
この微分方程式の問題でも「重ね合わせの原理」は明らかに成り立ち、$C_{0}e^{\frac{W_{0}(t)}{t}x}+C_{-1}e^{\frac{W_{-1}(t)}{t}x}\ (C_{0},C_{-1}:任意定数)$はすべて解です。
(なお、$t=-\frac{1}{e}$のとき、$W_{0}(-\frac{1}{e})$も$W_{-1}(-\frac{1}{e})$も同じ$-1$になります。)
$t<-\frac{1}{e}$のときは、$xe^x=t$を満たす実数$x$が存在しないので、解はなさそうに思えます。

$f'(x)=f(x+\frac{1}{3})$を満たす関数の例$f(x)=2e^{-3W_{0}(-\frac{1}{3})x}-\frac{1}{2}e^{-3W_{-1}(-\frac{1}{3})x}$
青線$f(x+\frac{1}{3})$と赤線$f'(x)$が重なっている

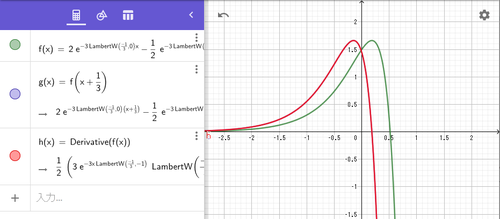f'(x)=f(x+1/3)

というわけで、$f'(x)=f(x-t)$を満たす実関数は以下のようになりそうです。
$f(x)=\begin{cases} Ce^{\frac{W_{0}(t)}{t}x} & (t>0)(C:任意定数) \\ Ce^x & (t=0)(C:任意定数) \\ C_{0}e^{\frac{W_{0}(t)}{t}x}+C_{-1}e^{\frac{W_{-1}(t)}{t}x} & (-\frac{1}{e}\leqq t<0)(C_{0},C_{-1}:任意定数) \qquad \\ 存在しない & (t<-\frac{1}{e}) \end{cases}$
$1$階の微分方程式なのに、任意定数が2種類出てくるとは・・・個人的にビックリです。
なお、$t\rightarrow0$とすると、$\frac{W_{0}(t)}{t}\rightarrow1$となるので、$t=0$のときの一般解$f(x)=Ce^x$と一致します。

・・・しかし、実はこれは正しくないんです。
例えば$f(x)=\cos(x)$とすると、
$f'(x)=-\sin(x)=\cos(x+\frac{\pi}{2})=f(x+\frac{\pi}{2})$なので、
$t=-\frac{\pi}{2}$の場合に該当します。
しかし、この場合は上記の場合分けでは「存在しない」となっています。
まだ見つかっていない解があるようです。
原因は$W(x)$の"イタズラ"です。

複素関数$W(z)$を調べる

$W(x)$は値域が実数の範囲では$2$種類ありますが、複素数の範囲では無限種類あります。
つまり、複素数$z$に対し、$we^w=z$を満たす複素数$w$は無限にあるのです。これらを$W_{n}(z)\ (n\in\mathbb{Z})$と書くことにします(ただし、例外として$z=0$のときは$w=W_{0}(0)=0$しかありません)。
(厳密には、$W_{0}(z)$から、複素関数の解析接続を使って$w=W_{n}(z)\ (n\in\mathbb{Z})$を定義するのですが、基本的には虚部の小さいほうから「$\cdots,W_{-2}(z),W_{-1}(z),W_{0}(z),W_{1}(z),W_{2}(z),\cdots$」となっていると思って差し支えはないようです。)

$W_{n}(t)$を実数の範囲だけで考えていたとき、$t\ne 0$に対して、$f'(x)=f(x-t)$の解には
$e^{\frac{W_{n}(t)}{t}x}$の定数倍と和で組み合わせたものがありました。($C_{0}e^{\frac{W_{0}(t)}{t}x}+C_{-1}e^{\frac{W_{-1}(t)}{t}x}$のことです。)
これは、$t$が複素数、$n$が$0,-1$以外でも同じです。

任意の整数$n$に対して、
$W_{n}((a+ib)e^{a+ib})=a+ib$となる複素数$a+ib\ (a,b\in\mathbb{R})$があります。
そこで、$t=(a+ib)e^{a+ib}$とすると、
$e^{\frac{W_{n}(t)}{t}x}=e^{\frac{a+ib}{(a+ib)e^{a+ib}}x}=e^{e^{-a-ib}x}$となります。

$W_{n}(ze^z)=z$となる$n$が何かを複素平面にプロットしたものがこちら(英語版Wikipedia "Lambert W function")

ただ、ここで求めたいのは「実数」$t$に対する$f'(x)=f(x-t)$の解なので、
$t=(a+ib)e^{a+ib}$が実数であってほしいわけです。
$b=0$なら、上記の実数の範囲だけの話なので、$b\ne 0$であるとします。

$(a+ib)e^{a+ib}$を実部と虚部に分けると、
\begin{eqnarray*} & & (a+ib)e^{a+ib}\\ & = & (a+ib)e^a(\cos(b)+i\sin(b))\\ & = & e^a(a\cos(b)-b\sin(b))+ie^a(b\cos(b)+a\sin(b))\\ \end{eqnarray*}

なので、$(a+ib)e^{a+ib}$が実数になるには、$e^a(b\cos(b)+a\sin(b))=0$でなければなりません。
よって、$a=-b\cot(b)$です。
このとき、$t=e^{-b\cot(b)}(-b\cot(b)\cos(b)-b\sin(b))=-be^{-b\cot(b)}\cosec(b)$です。

$y=-x\cot(x)$のグラフ
$a=-b\cot(b)$のとき、$(a+ib)e^{a+ib}$が実数になる

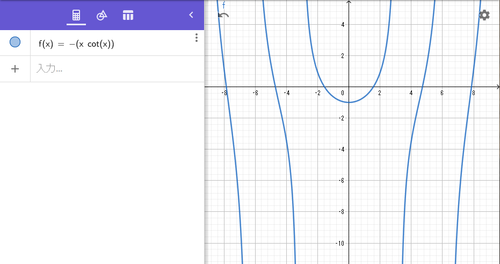-xcot(x)

$y=-xe^{-x\cot(x)}\cosec(x)$のグラフ
$0$でない実数$t$に対し、$t=-be^{-b\cot(b)}\cosec(b)$となる$b$が無限個存在する

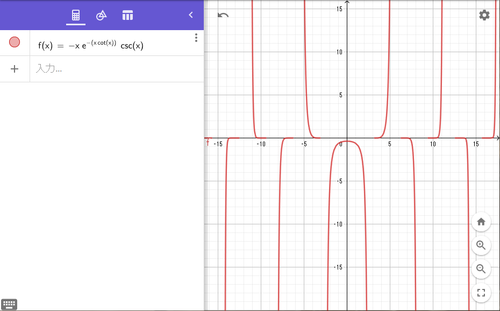-xe^(-xcot(x))cosec(x)

また、$e^{\frac{W_{n}(t)}{t}x}$も実部と虚部に分解すると、
\begin{eqnarray*} e^{\frac{W_{n}(t)}{t}x}& = & e^{e^{-a-ib}x}\\ & = & e^{e^{b\cot(b)-ib}x}\\ & = & e^{e^{b\cot(b)}(\cos(b)-i\sin(b))x}\\ & = & e^{e^{b\cot(b)}\cos(b)x}\cos(e^{b\cot(b)}\sin(b)x)-ie^{e^{b\cot(b)}\cos(b)x}\sin(e^{b\cot(b)}\sin(b)x) \end{eqnarray*}

従って、実数$b$に対して、$f'(x)=f(x-t)$つまり$f'(x)=f(x+be^{-b\cot(b)}\cosec(b))$の解には、
$e^{e^{b\cot(b)}\cos(b)x}\cos(e^{b\cot(b)}\sin(b)x)-ie^{e^{b\cot(b)}\cos(b)x}\sin(e^{b\cot(b)}\sin(b)x)$(の定数倍)があることがわかりました。

しかし、欲しい解は「実関数」です。
$ie^{e^{b\cot(b)}\cos(b)x}\sin(e^{b\cot(b)}\sin(b)x)$が邪魔になっています。
この邪魔な虚部をなくしましょう。

方法としては、$2$つの解の和がまた解になることを使って、虚部を相殺することです。
複素数$a-ib\ (a,b\in\mathbb{R})$に対して、
$W_{m}((a-ib)e^{a-ib})=a-ib$となる$m$があります。

そこで、今度は$t=(a-ib)e^{a-ib}$とすると、
$e^{\frac{W_{m}(t)}{t}x}=e^{\frac{a-ib}{(a-ib)e^{a-ib}}x}=e^{e^{-a+ib}x}$となります。
同様に$t$が実数であってほしいのですが、実部と虚部に分解すると、
$(a-ib)e^{a-ib}=e^a(a\cos(b)-b\sin(b))-ie^a(b\cos(b)+a\sin(b))$であり、
$(a+ib)e^{a+ib}$のときと虚部の符号が違うだけなので、$a=-b\cot(b)$が$t$が実数になる条件です。
さらに実部が同じなので、$a=-b\cot(b)$ならば$t=(a+ib)e^{a+ib}=(a-ib)e^{a-ib}=-be^{-b\cot(b)}\cosec(b)\in\mathbb{R}$になります。
つまり、実数$t\ne 0$に対し、$W_{n}(t)=a+ib,W_{m}(t)=a-ib$ですね。

$e^{\frac{W_{m}(t)}{t}x}$も実部と虚部に分解すると、
\begin{eqnarray*} e^{\frac{W_{m}(t)}{t}x}& = & e^{e^{-a+ib}x}\\ & = & e^{e^{b\cot(b)+ib}x}\\ & = & e^{e^{b\cot(b)}(\cos(b)+i\sin(b))x}\\ & = & e^{e^{b\cot(b)}\cos(b)x}\cos(e^{b\cot(b)}\sin(b)x)+ie^{e^{b\cot(b)}\cos(b)x}\sin(e^{b\cot(b)}\sin(b)x) \end{eqnarray*}
これも$e^{\frac{W_{n}(t)}{t}x}$と虚部の符号が違うだけです。

よって、$e^{\frac{W_{n}(t)}{t}x}$と$e^{\frac{W_{m}(t)}{t}x}$を足し算すると、
$e^{\frac{W_{n}(t)}{t}x}+e^{\frac{W_{m}(t)}{t}x}=2e^{e^{b\cot(b)}\cos(b)x}\cos(e^{b\cot(b)}\sin(b)x)$
となって、実関数になります。

したがって、実数$t\ne 0$が与えられたとき、
$t=-be^{-b\cot(b)}\cosec(b)$となる実数$b$に対し、
$f(x)=e^{\frac{W_{n}(t)}{t}x}+e^{\frac{W_{m}(t)}{t}x}=2e^{e^{b\cot(b)}\cos(b)x}\cos(e^{b\cot(b)}\sin(b)x)$とすると、これは
$f'(x)=f(x-t)$の実関数の解になることが分かりました。
($n,m$によって、$b$の値は変わり、$2e^{e^{b\cot(b)}\cos(b)x}\cos(e^{b\cot(b)}\sin(b)x))$もさまざまな関数になります。)

実は、$n$と$m$の関係は、$t<0$のとき$m=-n-1$、$t>0$のとき$m=-n$なんです。
$t<0$の場合は、
$f(x)=e^{\frac{W_{3}(t)}{t}x}+e^{\frac{W_{-4}(t)}{t}x}$や、
$f(x)=e^{\frac{W_{6}(t)}{t}x}+e^{\frac{W_{-7}(t)}{t}x}$などが解です。
$t>0$の場合は、
$f(x)=e^{\frac{W_{3}(t)}{t}x}+e^{\frac{W_{-3}(t)}{t}x}$や、
$f(x)=e^{\frac{W_{6}(t)}{t}x}+e^{\frac{W_{-6}(t)}{t}x}$などが解です。
$n$はすべての整数をとれるので、無限にいろんな関数ができます。
そして、「重ね合わせの原理」から、これらをそれぞれ実数倍して足したものもすべて解になります。

$f(x)=e^{-\frac{W_{3}(-5)}{5}x}+e^{-\frac{W_{-4}(-5)}{5}x}$のグラフ

$f(x)=e^{\frac{W_{3}(5)}{5}x}+e^{\frac{W_{-3}(5)}{5}x}$のグラフ

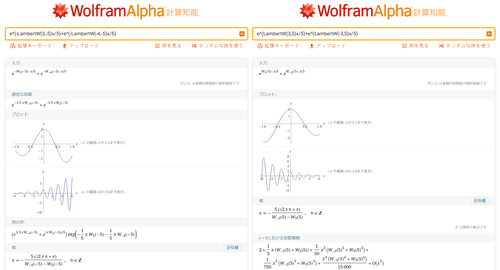具体例

したがって、新たにこれらの実関数の解が見つかりました。
$f(x)=\begin{cases} \displaystyle\sum_{n=0}^{\infty}C_{n}\Big(e^{\frac{W_{n}(t)}{t}x}+e^{\frac{W_{-n}(t)}{t}x}\Big) & (t>0)(C_n:任意定数) \qquad \\ \displaystyle\sum_{n=0}^{\infty}C_{n}\Big(e^{\frac{W_{n}(t)}{t}x}+e^{\frac{W_{-n-1}(t)}{t}x}\Big) & (t<0)(C_n:任意定数) \end{cases}$
(ただし、任意定数$C_{n}$は、この関数項級数の無限和が任意の実数$x$で収束して、項別微分可能になることを前提とする。)

例えば、実数の範囲だけではうまく説明できなかった$f(x)=\cos(x)$の場合は、
$W_{0}(-\frac{\pi}{2})=\frac{i\pi}{2},\ W_{-1}(-\frac{\pi}{2})=-\frac{i\pi}{2}$であることを使って、
$f(x)=\frac{1}{2}\Big(e^{\frac{W_{0}(-\pi/2)}{-\pi/2}x}+e^{\frac{W_{-1}(-\pi/2)}{-\pi/2}x}\Big)$となり
$t=-\frac{\pi}{2}$の場合になることが分かります。

今わかっている解をまとめると

実数$t$に対し、$f'(x)=f(x-t)$を満たす実関数は、
$f(x)=e^{sx}$の形に注目して$W(t)$を値域が実数の関数として見たときに、以下の解が見つかりました。

$f(x)=\begin{cases} Ce^{\frac{W_{0}(t)}{t}x} & (t>0)(C:任意定数) \\ Ce^x & (t=0)(C:任意定数) \\ C_{0}e^{\frac{W_{0}(t)}{t}x}+C_{-1}e^{\frac{W_{-1}(t)}{t}x} & (-\frac{1}{e}\leqq t<0)(C_{0},C_{-1}:任意定数) \qquad \\ 存在しない & (t<-\frac{1}{e}) \end{cases}$

そして、$W(t)$を値域が複素数の関数として見て、$2$つの複素関数の解の和で実関数になってくれるものを調べて、以下の解が見つかりました。

$f(x)=\begin{cases} \displaystyle\sum_{n=0}^{\infty}C_{n}\Big(e^{\frac{W_{n}(t)}{t}x}+e^{\frac{W_{-n}(t)}{t}x}\Big) & (t>0)(C_n:任意定数) \qquad \\ \displaystyle\sum_{n=0}^{\infty}C_{n}\Big(e^{\frac{W_{n}(t)}{t}x}+e^{\frac{W_{-n-1}(t)}{t}x}\Big) & (t<0)(C_n:任意定数) \end{cases}$

これらをきれいにまとめるとこのようになります。

$1$階の微分方程式なのに、任意定数が無限個登場するとは個人的にビックリです。
これも$W(t)$の多価性(しかも無限価)の影響で、さらに複素対数関数とは違い、定数の差だけではないからですね。
$f(0)=1,f(1)=0,f(5)=-7,\cdots$のようにいくら初期値を設定しても、特殊解を一通りに定めることができない可能性が高いです。
想像以上に解がいっぱいあるってことですね・・・

もしかしたらまだあるかも・・・

かなりの実関数の解を見つけたつもりなんですが、もしかしたらまだあるかもしれないです。。。
もし$f(x)$が実数全体で解析関数だったら、上記の解だけだと思うんです。
だけど、非解析的で無限回微分可能な解となると・・・他にないことを証明するのは自分の実力じゃ無理でしたので、わかる人は教えていただきたいです・・・

以上、読んでいただきありがとうございました。

(2021/02/07 追記)
J_Koizumiさんにより、実数全体で解析的でなくても、$f'(x)=f(x-t)\ (t\ne 0)$を満たす実関数の存在が確認できました。
ありがとうございます！！！
詳しくはコメント欄をご覧ください。
やはり想像以上に解がいっぱいあるってことですね・・・