文献あり

積分が解けませんでした

125

さっきDon＠ld氏が難しそうな積分の問題( https://mathlog.info/articles/1750 ) が投稿されていたので, それを考えたいと思います.
$$\begin{eqnarray} \int_{-\infty}^{\infty}\frac{e^{\pi t/2}\left(2t\cos\left(e^{\pi t/2}+\frac{\pi}4\right)+(t^2+3)\sin\left(e^{\pi t/2}+\frac{\pi}4\right)\right)}{(t^2+1)(t^2+9)}\,dt \end{eqnarray}$$
まず収束性が問題です. 積分の中身は$t\to\infty$で指数関数的に無限に発散しているので, 発散しているように見えるかもしれません. まず, $(-\infty, 0)$の範囲では絶対収束しています. $0\lt \alpha$とします. 置換$e^{\alpha x}\mapsto x$により,
$$\begin{eqnarray} \int_{0}^{\infty}e^{\alpha x}f(e^{\alpha x})\,dx=\frac 1{\alpha}\int_1^{\infty}f(x)\,dx \end{eqnarray}$$
という感じになるので, 被積分関数の$(0,\infty)$での積分は$\alpha =\frac{\pi}2$として,
$$\begin{eqnarray} \frac 1{\alpha}\int_1^{\infty}\frac{\frac{2}{\alpha}(\ln x)\cos\left(x+\frac{\pi}4\right)+\left(\left(\frac{\ln x}{\alpha}\right)^2+3\right)\sin\left(x+\frac{\pi}4\right)}{\left(\left(\frac{\ln x}{\alpha}\right)^2+1\right)\left(\left(\frac{\ln x}{\alpha}\right)^2+9\right)}\,dx \end{eqnarray}$$
少し複雑で分かりにくいですが, 部分分数分解を用いて展開すると, $\alpha, \beta$を実数として, $n=0,1$に対し,
$$\begin{eqnarray} \int_1^{\infty}\frac{(\ln^n x)\sin (x+\alpha)}{\ln^2 x+\beta^2}\,dx \end{eqnarray}$$
が収束することを示せば十分です. ここで, 補題を用意します.

$a_n$が非負で狭義単調減少な数列で,
$$\begin{eqnarray} \lim_{n\to\infty}a_n=0 \end{eqnarray}$$
であるとき,
$$\begin{eqnarray} \sum_{n=0}^{\infty}(-1)^na_n \end{eqnarray}$$
は収束する.

これは簡単なので, 証明は省略する.

$[0,\infty)$で定義された非負連続関数$f(x)$を, 十分大きな$0\lt M$をとれば, $[M,\infty)$で狭義単調減少な関数で,
$$\begin{eqnarray} \lim_{x\to\infty}f(x)=0 \end{eqnarray}$$
とすると,
$$\begin{eqnarray} \int_0^{\infty}f(x)\sin x\,dx \end{eqnarray}$$
は収束する.

$M\lt 2\pi N$となる, $N\in \mathbb{N}$をとると, $f(x)$は$[2\pi N,\infty)$で狭義単調減少である. また, $f$は$[0, 2\pi N]$で有界であるから,
$$\begin{eqnarray} \int_0^{\infty}f(x)\sin x\,dx&=&\int_0^{2\pi N}f(x)\sin x\, dx+\int_{2\pi N}^{\infty}f(x)\sin x\, dx\\ &=&\int_0^{2\pi N}f(x)\sin x\, dx+\int_0^{\infty}f(x+2\pi N)\sin x\, dx \end{eqnarray}$$
より, 第1項は収束するので, 第2項が収束することを示せばよいので, はじめから$[0,\infty)$で狭義単調減少な関数としてよい. このとき,
\begin{eqnarray} \int_0^{\infty}f(x)\sin x\,dx&=&\sum_{n=0}^{\infty}\int_{n\pi}^{(n+1)\pi}f(x)\sin x\,dx\\ &=&\sum_{n=0}^{\infty}(-1)^n\int_0^{\pi}f(x+n\pi)\sin x\,dx \end{eqnarray}
ここで, $f$は狭義単調減少だったから, $x\in (0,\pi)$で, $f(x+n\pi) \gt f(x+(n+1)\pi)$
よって,
$$\begin{eqnarray} a_n=\int_0^{\pi}f(x+n\pi)\sin x\,dx \end{eqnarray}$$
は狭義単調減少な数列である. また,
$$\begin{eqnarray} \lim_{n\to\infty}a_n&=&\lim_{n\to\infty}\int_0^{\pi}f(x+n\pi)\sin x\,dx\\ &\leq& \pi\lim_{n\to\infty}f(x+n\pi)\\ &=&0 \end{eqnarray}$$
である. よって, 補題1より積分は収束する.

さて, この補題を$\alpha$だけ平行移動することにより,
$$\begin{eqnarray} \int_1^{\infty}\frac{(\ln^n x)\sin (x+\alpha)}{\ln^2 x+\beta^2}\,dx \end{eqnarray}$$
の収束性が分かる. さて, もとの積分の値を求める方法を考えていきたい. 同様の置換により, 積分区間は$(-\infty,\infty)$から$(0,\infty)$になる. また, 上の分母をさらに部分分数分解することで,
$$\begin{eqnarray} \int_0^{\infty}\frac{\sin(x+\alpha)}{\ln x+\beta}\,dx \end{eqnarray}$$
の形の積分を求めればよいので,
$$\begin{eqnarray} h_{\pm}(\alpha)=\int_0^{\infty}\frac{e^{\pm ix}}{\ln x+i\alpha}\,dx \end{eqnarray}$$
とおいて, これを考えればよい. 以下, $\ln x$は十分小さな$\delta$をとって, 偏角$(-\pi+\delta, \pi+\delta)$で一価正則で$\ln e^{ix}=ix$となるような範囲で枝をとるとする.

$$\begin{eqnarray} h_{+}(\alpha)+h_{-}(\alpha+\pi)=\begin{cases} 0,\quad (0\lt\alpha\lt\pi)\\ 2\pi ie^{i(e^{-i\alpha}-\alpha)},\quad (-\pi\lt\alpha\lt 0) \end{cases}\\ h_{-}(\alpha)+h_{+}(\alpha-\pi)=\begin{cases} 0,\quad (-\pi\lt \alpha\lt 0)\\ -2\pi ie^{i(-e^{-i\alpha}-\alpha)},\quad (0\lt\alpha\lt \pi) \end{cases} \end{eqnarray}$$

以下のような積分路$C_{\vp}$を考える.
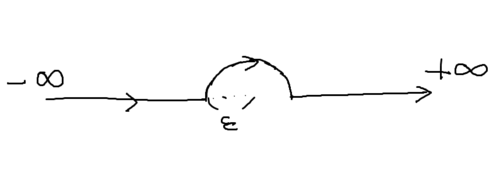積分路
すると,
$$\begin{eqnarray} \int_{C_{\vp}}\frac{e^{ix}}{\ln x+i\alpha}\,dx&=&\int_{\vp}^{\infty}\frac{e^{ix}}{\ln x+i\alpha}\,dx+\int_{\vp}^{\infty}\frac{e^{-ix}}{\ln x+i\alpha+i\pi}\,dx-i\vp\int_0^{\pi}\frac{e^{i\vp e^{ix}+ix}}{\ln\vp e^{ix}+i\alpha}\,dx \end{eqnarray}$$
$\vp\to 0$として, 第3項は$0$に収束する. よって,
$$\begin{eqnarray} \lim_{\vp\to 0}\int_{C_{\vp}}\frac{e^{ix}}{\ln x+i\alpha}\,dx=h_{+}(\alpha)+h_{-}\left(\alpha+\pi\right) \end{eqnarray}$$

今度は以下のように積分路$C$をとる.
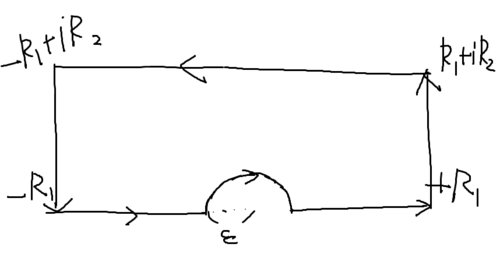積分路2
$$\begin{eqnarray} \int_{\pm R_1}^{\pm R_1+iR_2}\frac{e^{ix}}{\ln x+i\alpha}\,dx=e^{\pm iR_1}\int_0^{R_2}\frac{e^{-x}}{\ln(\pm R_1+ix)+i\alpha}\,dx \end{eqnarray}$$
は$R_1\to\infty$で$0$に収束し,
$$\begin{eqnarray} \int_{-\infty}^{\infty}\frac{e^{i(x+iR_2)}}{\ln(x+iR_2)+i\alpha}\,dx=e^{-R_2}\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}\frac{e^{ix}}{\ln(x+iR_2)+i\alpha}\,dx \end{eqnarray}$$
も$R_2\to\infty$で$0$に収束するので, $R_1,R_2\to\infty$で残るのは先ほどの$C_{\vp}$である. よって, $-\pi\lt\alpha\lt 0$のとき, $x=e^{-i\alpha}$の留数は$e^{i(e^{-i\alpha}-\alpha)}$であるから, 留数定理より,
$$\begin{eqnarray} h_{+}(\alpha)+h_{-}(\alpha+\pi)=\begin{cases} 0,\quad (0\lt\alpha\lt\pi-\delta)\\ 2\pi ie^{i(e^{-i\alpha}-\alpha)},\quad (-\pi\lt\alpha\lt 0) \end{cases} \end{eqnarray}$$

$\ln x$の主値の偏角を$(-\pi-\delta,\pi-\delta)$として, 点対称な積分路で$h_{-}$に対し全く同じ議論をすることにより,

$$\begin{eqnarray} h_{-}(\alpha)+h_{+}(\alpha-\pi)=\begin{cases} 0,\quad (-\pi+\delta\lt \alpha\lt 0)\\ -2\pi ie^{i(-e^{-i\alpha}-\alpha)},\quad (0\lt\alpha\lt \pi) \end{cases} \end{eqnarray}$$
ここで, $\delta\to 0$として,
$$\begin{eqnarray} h_{+}(\alpha)+h_{-}(\alpha+\pi)=\begin{cases} 0,\quad (0\lt\alpha\lt\pi)\\ 2\pi ie^{i(e^{-i\alpha}-\alpha)},\quad (-\pi\lt\alpha\lt 0) \end{cases}\\ h_{-}(\alpha)+h_{+}(\alpha-\pi)=\begin{cases} 0,\quad (-\pi\lt \alpha\lt 0)\\ -2\pi ie^{i(-e^{-i\alpha}-\alpha)},\quad (0\lt\alpha\lt \pi) \end{cases} \end{eqnarray}$$

さて, $\alpha=\frac{\pi}{2}$として, もとの積分を変形していきます.
$$\begin{eqnarray} I&=&\int_{-\infty}^{\infty}\frac{e^{\pi t/2}\left(2t\cos\left(e^{\pi t/2}+\frac{\pi}4\right)+(t^2+3)\sin\left(e^{\pi t/2}+\frac{\pi}4\right)\right)}{(t^2+1)(t^2+9)}\,dt\\ &=&\frac 1{\alpha}\int_0^{\infty}\frac{\frac{2}{\alpha}(\ln x)\cos\left(x+\frac{\pi}4\right)+\left(\left(\frac{\ln x}{\alpha}\right)^2+3\right)\sin\left(x+\frac{\pi}4\right)}{\left(\left(\frac{\ln x}{\alpha}\right)^2+1\right)\left(\left(\frac{\ln x}{\alpha}\right)^2+9\right)}\,dx\\ &=&\alpha\int_0^{\infty}\frac{2\alpha(\ln x)\cos\left(x+\frac{\pi}4\right)+\left(\ln^2 x+3\alpha^2\right)\sin\left(x+\frac{\pi}4\right)}{\left(\ln^2 x+\alpha^2\right)\left(\ln^2 x+9\alpha^2\right)}\,dx\\ &=&2\alpha^2\int_0^{\infty}\frac{(\ln x)\cos\left(x+\frac{\pi}4\right)+\alpha\sin\left(x+\frac{\pi}{4}\right)}{(\ln^2x+\alpha^2)(\ln^2x+(3\alpha)^2)}\,dx+\alpha\int_0^{\infty}\frac{\sin\left(x+\frac{\pi}{4}\right)}{\ln^2x+(3\alpha)^2}\,dx\\ &=&\frac 14\int_0^{\infty}\left((\ln x)\cos\left(x+\frac{\pi}4\right)+\alpha\sin\left(x+\frac{\pi}{4}\right)\right)\left(\frac 1{\ln^2x+\alpha^2}-\frac 1{\ln^2x+(3\alpha)^2}\right)\,dx\\ &+&\alpha\int_0^{\infty}\frac{\sin\left(x+\frac{\pi}{4}\right)}{\ln^2x+(3\alpha)^2}\,dx\\ &=&\frac 14\int_0^{\infty}\frac{(\ln x)\cos\left(x+\frac{\pi}4\right)}{\ln^2 x+\alpha^2}\,dx+\frac {\alpha}4\int_0^{\infty}\frac{\sin\left(x+\frac{\pi}4\right)}{\ln^2 x+\alpha^2}\,dx\\ &-&\frac 14\int_0^{\infty}\frac{(\ln x)\cos\left(x+\frac{\pi}4\right)}{\ln^2 x+(3\alpha)^2}\,dx+\frac{3\alpha}{4}\int_0^{\infty}\frac{\sin\left(x+\frac{\pi}{4}\right)}{\ln^2x+(3\alpha)^2}\,dx \end{eqnarray}$$

また, 任意の$\alpha$に対し,
$$\begin{eqnarray} h_{+}(\alpha)&=&\int_0^{\infty}\frac{e^{ix}}{\ln x+i\alpha}\,dx\\ &=&\int_0^{\infty}\frac{(\ln x-i\alpha)(\cos x+i\sin x)}{\ln^2 x+\alpha^2}\,dx\\ &=&\int_0^{\infty}\frac{(\ln x)\cos x+\alpha\sin x}{\ln^2 x+\alpha^2}\,dx+i\int_0^{\infty}\frac{(\ln x)\sin x-\alpha\cos x}{\ln^2 x+\alpha^2}\,dx\\ h_{-}(\alpha)&=&\int_0^{\infty}\frac{(\ln x)\cos x-\alpha\sin x}{\ln^2 x+\alpha^2}\,dx-i\int_0^{\infty}\frac{(\ln x)\sin x+\alpha\cos x}{\ln^2 x+\alpha^2}\,dx \end{eqnarray}$$

さて, 定理の1つ目の式に$\alpha=\frac{\pi}2$として,
$$\begin{eqnarray} &&h_{+}\left(\frac{\pi}{2}\right)+h_{-}\left(\frac{3\pi}{2}\right)=0 \end{eqnarray}$$

よって, 上の式は$\alpha=\frac{\pi}{2}$として,

$$\begin{eqnarray} &&\left(\int_0^{\infty}\frac{(\ln x)\cos x+\alpha\sin x}{\ln^2 x+\alpha^2}\,dx+\int_0^{\infty}\frac{(\ln x)\cos x-3\alpha\sin x}{\ln^2 x+(3\alpha)^2}\,dx\right)\\ &+&i\left(\int_0^{\infty}\frac{(\ln x)\sin x-\alpha\cos x}{\ln^2 x+\alpha^2}\,dx-\int_0^{\infty}\frac{(\ln x)\sin x+3\alpha\cos x}{\ln^2 x+(3\alpha)^2}\right)=0\\ \end{eqnarray}$$
これより,

$$\begin{eqnarray} &&\int_0^{\infty}\frac{(\ln x)\cos x+\alpha\sin x}{\ln^2 x+\alpha^2}\,dx+\int_0^{\infty}\frac{(\ln x)\cos x-3\alpha\sin x}{\ln^2 x+(3\alpha)^2}\,dx=0\\ &&\int_0^{\infty}\frac{(\ln x)\sin x-\alpha\cos x}{\ln^2 x+\alpha^2}\,dx-\int_0^{\infty}\frac{(\ln x)\sin x+3\alpha\cos x}{\ln^2 x+(3\alpha)^2}\,dx=0\\ \end{eqnarray}$$
この2つの式を足し合わせて,
$$\begin{eqnarray} \int_0^{\infty}\frac{(\ln x)\cos\left(x+\frac{\pi}{4}\right)-3\alpha\sin\left(x+\frac{\pi}{4}\right)}{\ln^2 x+(3\alpha)^2}\,dx=-\int_0^{\infty}\frac{(\ln x)\sin\left(x+\frac{\pi}{4}\right)-\alpha\cos\left(x+\frac{\pi}{4}\right)}{\ln^2 x+\alpha^2}\,dx \end{eqnarray}$$
これを先ほどの$I$の式に代入して, 加法定理で整理すると,
$$\begin{eqnarray} I&=&\frac{1}{2\sqrt{2}}\int_0^{\infty}\frac{(\ln x)\cos x+\alpha\sin x}{\ln^2 x+\alpha^2}\,dx \end{eqnarray}$$

ここで, 定理の1つ目の式に$\alpha=-\frac{\pi}{2}$を代入して,
$$\begin{eqnarray} &&h_{+}\left(-\frac{\pi}{2}\right)+h_{-}\left(\frac{\pi}{2}\right)=-\frac{2\pi}{e} \end{eqnarray}$$
であるから, これを$\alpha=\frac{\pi}{2}$として整理して,
$$\begin{eqnarray} \int_0^{\infty}\frac{(\ln x)\cos x-\alpha\sin x}{\ln^2 x+\alpha^2}=-\frac{\pi}{e} \end{eqnarray}$$
さて,

$$\begin{eqnarray} I&=&\frac{1}{2\sqrt{2}}\int_0^{\infty}\frac{(\ln x)\cos x+\alpha\sin x}{\ln^2 x+\alpha^2}\,dx\\ &=&\frac {\pi}{2\sqrt{2}}\int_0^{\infty}\frac{\sin x}{\ln^2 x+\alpha^2}\,dx-\frac{\pi}{2e\sqrt{2}} \end{eqnarray}$$
あれ, おかしいな.
$$\begin{eqnarray} \int_0^{\infty}\frac{\sin x}{\ln^2 x+\alpha^2}\,dx \end{eqnarray}$$
これを求める方法があるのだろうか. ということは僕の方針がちょっと微妙だったのかもしれません. 最後の形をまとめておきます.

$$\begin{eqnarray} I=\frac {\pi}{2\sqrt{2}}\int_0^{\infty}\frac{\sin x}{\ln^2 x+(\pi/2)^2}\,dx-\frac{\pi}{2e\sqrt{2}} \end{eqnarray}$$

最後まで読んでいただきありがとうございました.