積分botを解けるだけ解く, その4

途中で, $t=\tan x$の置換をします. また, $\phi(\phi-1)=1$であることを用いることができます.
$$\begin{eqnarray*} \int_0^{2\pi}\frac{x}{\phi-\cos^2 x}\,dx&=&\frac 12\left(\int_0^{2\pi}\frac{x}{\phi-\cos^2 x}\,dx+\int_0^{2\pi}\frac{2\pi-x}{\phi-\cos^2 x}\,dx\right)\\ &=&\pi\int_0^{2\pi}\frac 1{\phi-\cos^2 x}\,dx\\ &=&4\pi\int_0^{\pi/2}\frac 1{\phi-\cos^2 x}\,dx\\ &=&4\pi\int_0^{\infty}\frac 1{\phi(1+t^2)-1}\,dt\\ &=&\frac{4\pi}{\sqrt{\phi(\phi-1)}}\int_0^{\infty}\frac 1{1+t^2}\,dt\\ &=&2\pi^2 \end{eqnarray*}$$

変数変換$x_k\to\frac{x_k}{a_k}$により,
$$\begin{eqnarray*} \int_{\mathbb{R}^n}\frac{\sin\sum_{k=1}^nx_k}{\sum_{k=1}^nx_k}\prod_{k=1}^n\frac{\sin x_k}{x_k}\,dx_k=\pi^n \end{eqnarray*}$$
を示せばよい. まず, $0\lt a\lt 1$に対し, $x_k\to-x_k$の置換により,
$$\begin{eqnarray*} \int_{\mathbb{R}^n}\sin\left(a\sum_{k=1}^nx_k\right)\prod_{k=1}^n\frac{\sin x_k}{x_k}\,dx_k&=&-\int_{\mathbb{R}^n}\sin\left(a\sum_{k=1}^nx_k\right)\prod_{k=1}^n\frac{\sin x_k}{x_k}\,dx_k=0 \end{eqnarray*}$$
ここで, $n$に関する帰納法により, $0\lt a\lt 1$に対し,
$$\begin{eqnarray*} \int_{\mathbb{R}^n}\cos\left(a\sum_{k=1}^nx_k\right)\prod_{k=1}^n\frac{\sin x_k}{x_k}\,dx_k=\pi^n \end{eqnarray*}$$
であることを示す. $n-1$まで成立するとすると,
$$\begin{eqnarray*} &&\int_{\mathbb{R}^n}\cos\left(a\sum_{k=1}^nx_k\right)\prod_{k=1}^n\frac{\sin x_k}{x_k}\,dx_k\\ &=&\int_{\mathbb{R}^n}\cos\left(a\sum_{k=1}^{n-1}x_k+ax_n\right)\prod_{k=1}^n\frac{\sin x_k}{x_k}\,dx_k\\ &=&\int_{\mathbb{R}^n}\cos\left(a\sum_{k=1}^{n-1}x_k\right)\cos ax_n\prod_{k=1}^n\frac{\sin x_k}{x_k}\,dx_k-\int_{\mathbb{R}^n}\sin\left(a\sum_{k=1}^{n-1}x_k\right)\sin ax_n\prod_{k=1}^n\frac{\sin x_k}{x_k}\,dx_k\\ &=&\int_{-\infty}^{\infty}\frac{\sin x_n\cos ax_n}{x_n}\,dx_n\int_{\mathbb{R}^{n-1}}\cos\left(a\sum_{k=1}^{n-1}x_k\right)\prod_{k=1}^{n-1}\frac{\sin x_k}{x_k}\,dx_k\\ &-&\int_{-\infty}^{\infty}\frac{\sin x_n\sin ax_n}{x_n}\,dx_n\int_{\mathbb{R}^{n-1}}\sin\left(a\sum_{k=1}^{n-1}x_k\right)\prod_{k=1}^{n-1}\frac{\sin x_k}{x_k}\,dx_k\\ &=&\pi\cdot\pi^{n-1}-0\\ &=&\pi^n \end{eqnarray*}$$
最後の変形は帰納法の仮定と,
$$\begin{eqnarray*} \int_{-\infty}^{\infty}\frac{\sin x\cos ax}{x}\,dx&=&\frac 12\int_{-\infty}^{\infty}\frac{\sin(1+a)x+\sin(1-a)x}{x}\,dx\\ &=&\pi \end{eqnarray*}$$
であることを用いた. よって,
$$\begin{eqnarray*} \int_{\mathbb{R}^n}\cos\left(a\sum_{k=1}^nx_k\right)\prod_{k=1}^n\frac{\sin x_k}{x_k}\,dx_k=\pi^n \end{eqnarray*}$$
において, $a$を$0$から$1$まで積分し, 積分順序の交換をして,
$$\begin{eqnarray*} \int_{\mathbb{R}^n}\frac{\sin\sum_{k=1}^nx_k}{\sum_{k=1}^nx_k}\prod_{k=1}^n\frac{\sin x_k}{x_k}\,dx_k=\pi^n \end{eqnarray*}$$
を得る.

$$\begin{eqnarray*} &&\frac{d}{da}\arctan\frac{\sqrt{\sqrt{1+a^4}-1}}{a}\\ &=&\frac 1{1+\frac{\sqrt{1+a^4}-1}{a^2}}\left(\frac{\frac 1{2\sqrt{\sqrt{1+a^4}-1}}\frac{4a^3}{2\sqrt{1+a^4}}a-\sqrt{\sqrt{1+a^4}-1}}{a^2}\right)\\ &=&\frac{1}{a^2+\sqrt{1+a^4}-1}\left(\frac{a^4}{\sqrt{1+a^4}\sqrt{\sqrt{1+a^4}-1}}-\sqrt{\sqrt{1+a^4}-1}\right)\\ &=&\frac{1}{a^2+\sqrt{1+a^4}-1}\frac{\sqrt{1+a^4}-1}{\sqrt{1+a^4}\sqrt{\sqrt{1+a^4}-1}}\\ &=&\frac 1{\sqrt{2(\sqrt{1+a^4}-1)(\sqrt{1+a^4}+a^2)}}\sqrt{\frac{\sqrt{1+a^4}-1}{1+a^4}}\\ &=&\frac 1{\sqrt{2}}\sqrt{\frac{\sqrt{1+a^2}-a^2}{1+a^4}} \end{eqnarray*}$$
より, 示された.

まず,
$$\begin{eqnarray*} I&:=&\int_{-\infty}^{\infty}\frac{e^{i\pi x^2}}{1+2\cosh\frac{2\pi x}{\sqrt{3}}}\,dx \end{eqnarray*}$$
と置く, 被積分関数は$x=\pm\frac i{\sqrt{3}}$に極をもつが, 虚部が$\pm\frac i{\sqrt{3}}$の直線上で主値積分を考えることができる.
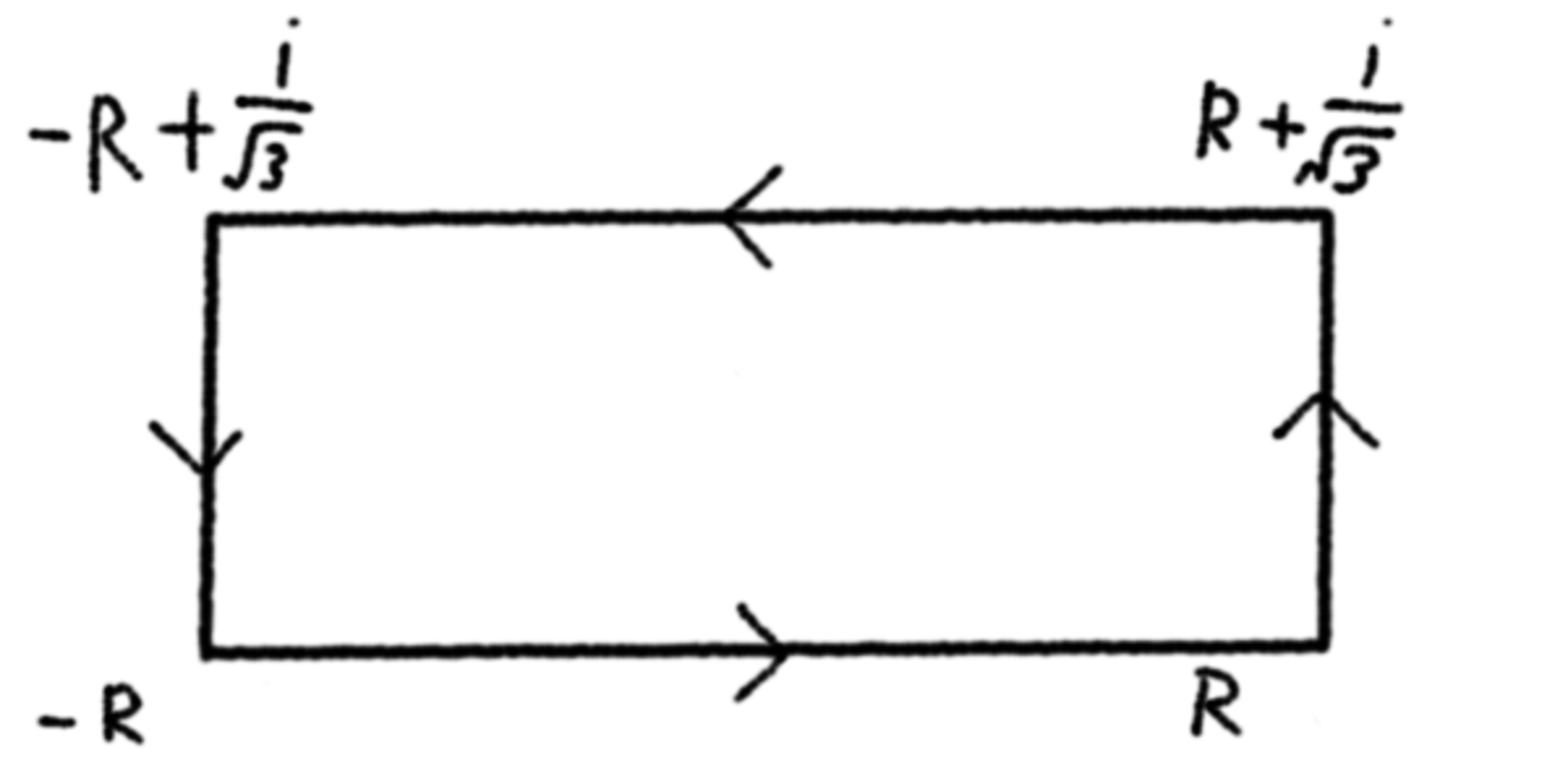積分路1
上のような積分路で積分をすると, 主値積分を考えるので, $x=\frac i{\sqrt{3}}$における留数の半分が含まれているとみなせて,
$$\begin{eqnarray*} I&=&\int_{-\infty}^{\infty}\frac{e^{i\pi x^2}}{1+2\cosh\frac{2\pi x}{\sqrt{3}}}\,dx\\ &=&\int_{-\infty}^{\infty}\frac{e^{i\pi(x+i/\sqrt{3})^2}}{1+2\cosh\left(\frac{2\pi x}{\sqrt{3}}+\frac{2\pi i}{3}\right)}\,dx+\pi i Res_{x=\frac i3}\frac{e^{i\pi x^2}}{1+2\cosh\frac{2\pi x}{\sqrt{3}}}\\ &=&e^{-i\pi/3}\int_{-\infty}^{\infty}\frac{e^{i\pi x^2-2\pi x/\sqrt{3}}}{1+2\cosh\left(\frac{2\pi x}{\sqrt{3}}+\frac{2\pi i}{3}\right)}\,dx+\frac 12e^{-i\pi/3}\\ &=&e^{-i\pi/3}\int_{-\infty}^{\infty}\frac{e^{i\pi x^2+2\pi x/\sqrt{3}}}{1+2\cosh\left(\frac{2\pi x}{\sqrt{3}}-\frac{2\pi i}{3}\right)}\,dx+\frac 12e^{-i\pi/3} \end{eqnarray*}$$
よって,
$$\begin{eqnarray*} \int_{-\infty}^{\infty}\frac{e^{i\pi x^2-2\pi x/\sqrt{3}}}{1+2\cosh\left(\frac{2\pi x}{\sqrt{3}}+\frac{2\pi i}{3}\right)}\,dx&=&e^{i\pi/3}I-\frac 12\\ \int_{-\infty}^{\infty}\frac{e^{i\pi x^2+2\pi x/\sqrt{3}}}{1+2\cosh\left(\frac{2\pi x}{\sqrt{3}}-\frac{2\pi i}{3}\right)}\,dx&=&e^{i\pi/3}I-\frac 12\\ \end{eqnarray*}$$
ここで, $y=e^{-2\pi x/\sqrt{3}}, \omega=e^{2\pi i/3}$とすると,
$$\begin{eqnarray*} &&\frac 1{1+2\cosh\frac{2\pi x}{\sqrt{3}}}=\frac 1{1+y^{-1}+y}=\frac{y(1-y)}{1-y^3}\\ &&\frac {e^{-2\pi x/\sqrt{3}}}{1+2\cosh\left(\frac{2\pi x}{\sqrt{3}}+\frac{2\pi i}3\right)}=\frac{y}{1+\omega y^{-1}+\omega^{2} y}=\frac{\omega^{2}y^2(1-\omega^{2} y)}{1-y^3}\\ &&\frac {e^{2\pi x/\sqrt{3}}}{1+2\cosh\left(\frac{2\pi x}{\sqrt{3}}-\frac{2\pi i}3\right)}=\frac{y^{-1}}{1+\omega^{2}y^{-1}+\omega y}=\frac{\omega (1-\omega y)}{1-y^3} \end{eqnarray*}$$
よって,
$$\begin{eqnarray*} \omega\frac{y(1-y)}{1-y^3}+\omega^2\frac{\omega^{2}y^2(1-\omega^{2} y)}{1-y^3}+\omega^2\frac{\omega(1-\omega y)}{1-y^3}=1 \end{eqnarray*}$$
より,
$$\begin{eqnarray*} e^{i\pi/4}&=&\int_{-\infty}^{\infty}e^{i\pi x^2}\,dx\\ &=&\int_{-\infty}^{\infty}e^{i\pi x^2}\left(\frac{e^{2\pi i/3}}{1+2\cosh\frac{2\pi x}{\sqrt{3}}}+ \frac{e^{-2\pi i/3-2\pi x/\sqrt{3}}}{1+2\cosh\left(\frac{2\pi x}{\sqrt{3}}+\frac{2\pi i}{3}\right)}+\frac{e^{-2\pi i/3+2\pi x/\sqrt{3}}}{1+2\cosh\left(\frac{2\pi x}{\sqrt{3}}-\frac{2\pi i}{3}\right)}\right)\,dx\\ &=&e^{2\pi i/3}I+2e^{-2\pi i/3}\left(e^{i\pi/3}I-\frac 12\right)\\ &=&(e^{2\pi i/3}+2e^{-i\pi/3})I-e^{-2\pi i/3} \end{eqnarray*}$$
よって,
$$\begin{eqnarray*} I&=&\frac{e^{i\pi/4}+e^{-2\pi i/3}}{e^{2\pi i/3}+2e^{-i\pi/3}}\\ &=&e^{i\pi/3}e^{i\pi/4}+e^{-i\pi/3}\\ &=&\frac{1+i\sqrt{3}}2\frac{\sqrt{2}+i\sqrt{2}}{2}+\frac{1-i\sqrt{3}}{2}\\ &=&\frac{2+\sqrt{2}-\sqrt{6}}{4}+i\left(\frac{\sqrt{2}+\sqrt{6}-2\sqrt{3}}{4}\right) \end{eqnarray*}$$
あとは, $I$の実部と虚部を比較すればよい.

まず,
$$\begin{eqnarray*} y=\frac 1{1+\frac{f(x)}{f(a+b-x)}} \end{eqnarray*}$$
と置いて,
$$\begin{eqnarray*} \sqrt{1+\sqrt{y}}-\sqrt{1-\sqrt{y}}&=&\frac{2\sqrt{y}}{\sqrt{1+\sqrt{y}}+\sqrt{1-\sqrt{y}}}\\ &=&\sqrt{2}\frac{\sqrt{y}}{\sqrt{1+\sqrt{1-y}}}\\ &=&\sqrt{2}\sqrt{\frac{y}{1+\sqrt{1-y}}}\\ &=&\sqrt{2}\sqrt{\frac{f(a+b-x)}{\sqrt{f(x)+f(a+b-x)}(\sqrt{f(x)+f(a+b-x)}+\sqrt{f(x)})}}\\ &=&\sqrt{2}\sqrt{\frac{\sqrt{f(x)+f(a+b-x)}-\sqrt{f(x)}}{\sqrt{f(x)+f(a+b-x)}}}\\ &=&\sqrt{2}\sqrt{1-\frac{1}{\sqrt{1+\frac{f(a+b-x)}{f(x)}}}} \end{eqnarray*}$$
よって,
$$\begin{eqnarray*} \int_a^b\sqrt{1+\sqrt{y}}\,dx=\int_a^b\sqrt{1-\sqrt{y}}\,dx+\sqrt{2}\int_a^b\sqrt{1-\frac 1{\sqrt{1+\frac{f(a+b-x)}{f(x)}}}}\,dx \end{eqnarray*}$$
この最後の項に, $x\to a+b-x$の置換をすればよい.

$x\to\frac{(1+p)x}{p+x}$の置換により,
$$\begin{eqnarray*} B(a,b)&=&\int_0^1x^{a-1}(1-x)^{b-1}\,dx\\ &=&(1+p)^ap^b\int_0^1x^{a-1}(1-x)^{b-1}(p+x)^{-a-b}\,dx \end{eqnarray*}$$
よって,
$$\begin{eqnarray*} \int_0^1x^{a-1}(1-x)^{b-1}(p+x)^{-a-b}\,dx=\frac{B(a,b)}{(1+p)^ap^b} \end{eqnarray*}$$

$$\begin{eqnarray*} K(x)=\int_0^{\pi/2}\frac{1}{\sqrt{1-y^2}\sqrt{1-x^2y^2}}\,dy \end{eqnarray*}$$
より,
$$\begin{eqnarray*} I(m,1)&=&\int_0^1K(x^{1/m})\,dx\\ &=&m\int_0^1x^{m-1}K(x)\,dx\\ &=&m\int_0^1\int_0^1\frac{x^{m-1}}{\sqrt{1-y^2}\sqrt{1-x^2y^2}}\,dxdy\\ &=&m\int_0^1\int_0^y\frac{x^{m-1}y^{-m}}{\sqrt{1-y^2}\sqrt{1-x^2}}\,dxdy \end{eqnarray*}$$
ここで, $x\to\sin x, y\to\sin y$とすると,
$$\begin{eqnarray*} \int_0^1\int_0^y\frac{x^{m-1}y^{-m}}{\sqrt{1-y^2}\sqrt{1-x^2}}\,dxdy&=&\int_0^{\pi/2}\int_0^y\frac{\sin^{m-1} x}{\sin^m y}\,dxdy\\ &=&\int_0^{\pi/2}\int_x^{\pi/2}\frac{\sin^{m-1}x}{\sin^m y}\,dydx \end{eqnarray*}$$
$m$が偶数, $m=2r$のとき, 不定積分,
$$\begin{eqnarray*} \int \frac{1}{\sin^{2r} x}\,dx&=&-\frac{2^{2r}}{r\binom{2r}r}\cos x\sum_{k=0}^{r-1}\frac{\binom{2k}k}{(2\sin x)^{2k+1}} \end{eqnarray*}$$
を用いて,
$$\begin{eqnarray*} &&\int_0^{\pi/2}\int_x^{\pi/2}\frac{\sin^{2r-1}x}{\sin^{2r} y}\,dydx\\ &=&\frac{2^{2r}}{r\binom{2r}r}\int_0^{\pi/2}\cos x\sin^{2r-1}x\sum_{k=0}^{r-1}\frac{\binom{2k}k}{(2\sin x)^{2k+1}}\,dx\\ &=&\frac{2^{2r}}{r\binom{2r}r}\sum_{k=0}^{r-1}\frac{\binom{2k}k}{2^{2k+1}}\int_0^{\pi/2}\cos x\sin^{2r-2k-2}x\,dx\\ &=&\frac{2^{2r-1}}{r\binom{2r}{r}}\sum_{k=0}^{r-1}\frac{\binom{2k}{k}}{2^{2k}(2r-2k-1)} \end{eqnarray*}$$
$m$が奇数, $m=2r+1$のとき, 不定積分,
$$\begin{eqnarray*} \int \frac{1}{\sin^{2r+1} x}\,dx&=&\frac 1{2^{2r}}\binom{2r}{r}\ln\tan\frac x2-\frac 1{2^{2r+1}}\binom{2r}{r}\cos x\sum_{k=1}^r\frac{1}{k\binom{2k}k}\left(\frac 2{\sin x}\right)^{2k} \end{eqnarray*}$$
を用いて,
$$\begin{eqnarray*} &&\int_0^{\pi/2}\int_x^{\pi/2}\frac{\sin^{2r}x}{\sin^{2r+1} y}\,dydx\\ &=&\frac 1{2^{2r+1}}\binom{2r}r\int_0^{\pi/2}\sin^{2r}x\cos x\sum_{k=1}^r\frac 1{k\binom{2k}k}\left(\frac{2}{\sin x}\right)^{2k}\,dx-\frac 1{2^{2r}}\binom{2r}r\int_0^{\pi/2}\sin^{2r}x\ln\tan\frac x2\,dx\\ &=&\frac 1{2^{2r+1}}\binom{2r}r\sum_{k=1}^r\frac {2^{2k}}{k\binom{2k}k}\int_0^{\pi/2}\sin^{2r-2k}x\cos x\,dx-\frac 1{2^{2r}}\binom{2r}r\int_0^{\pi/2}\sin^{2r}x\ln\tan\frac x2\,dx\\ &=&\frac 1{2^{2r+1}}\binom{2r}r\sum_{k=1}^r\frac {2^{2k}}{k(2r-2k+1)\binom{2k}k}-\frac 1{2^{2r}}\binom{2r}r\int_0^{\pi/2}\sin^{2r}x\ln\tan\frac x2\,dx\\ \end{eqnarray*}$$

ここで, $\tan\frac x2\to x$の置換により,
$$\begin{eqnarray*} -\int_0^{\pi/2}\sin^{2r}x\ln\tan\frac x2\,dx&=&-\int_0^1\left(\frac{2x}{1+x^2}\right)^{2r+1}\frac{\ln x}{x}\,dx\\ &=&\int_0^{\infty}\frac{x}{\cosh^{2r+1}x}\,dx \end{eqnarray*}$$
ここで, $\Re(s)$を十分大きくとって, Mellin変換を考える.
$$\begin{eqnarray*} \int_0^{\infty}\frac{x^{s-1}}{\cosh^{2r+1}x}\,dx&=&2^{2r+1}\int_0^{\infty}\frac{x^{s-1}e^{-(2r+1)x}}{(1+e^{-2x})^{2r+1}}\,dx\\ &=&2^{2r+1}\sum_{k=0}^{\infty}(-1)^k\binom{2r+k}{k}\int_0^{\infty}x^{s-1}e^{-(2r+2k+1)x}\,dx\\ &=&\frac{2^{2r+1}}{(2r)!}\sum_{k=0}^{\infty}(-1)^k\frac{(k+1)\cdots(k+2r)}{(2r+2k+1)^s}\\ &=&\frac{2^{2r+1}}{(2r)!}\sum_{k=0}^{\infty}(-1)^{k-r}\frac{(k+1-r)(k+2-r)\cdots(k+r)}{(2k+1)^s}\\ &=&\frac{2^{2r+1}}{(2r)!}\sum_{k=0}^{\infty}\frac{(-1)^{k-r}}{(2k+1)^s}\prod_{i=0}^{r-1}\left(\left(k+\frac 12\right)^2-\left(i+\frac 12\right)^2\right)\\ &=&\frac{2^{2r+1}\left(\frac 12\right)_n^2}{(2r)!}\sum_{k=0}^{\infty}\frac{(-1)^k}{(2k+1)^s}\prod_{i=0}^{r-1}\left(1-\frac{\left(2k+1\right)^2}{\left(2i+1\right)^2}\right)\\ &=&\frac{1}{2^{2r-1}}\binom{2r}{r}\sum_{k=0}^{\infty}\frac{(-1)^k}{(2k+1)^s}\prod_{i=0}^{r-1}\left(1-\frac{\left(2k+1\right)^2}{\left(2i+1\right)^2}\right)\\ \end{eqnarray*}$$
ここで, 自然数の組$(k_1,\dots,k_a)$に対し,
$$\begin{eqnarray*} t_n(k_1,\dots,k_a):=\sum_{0\leq n_1\lt n_2\lt\dots\lt n_a\lt n}\frac 1{(2n_1+1)^{k_1}\cdots(2n_a+1)^{k_a}} \end{eqnarray*}$$
と定義すると,
$$\begin{eqnarray*} \prod_{i=0}^{r-1}\left(1-\frac{\left(2k+1\right)^2}{\left(2i+1\right)^2}\right)&=&\sum_{j=0}^r(-1)^jt_r(\{2\}^j)(2k+1)^{2j} \end{eqnarray*}$$
ここで, $\{2\}^j$は$2$が$j$個並んだものを表し, $t_n(\{2\}^0)=t_n(\varnothing)=1$とする. これを先ほどの式に代入して,
$$\begin{eqnarray*} \int_0^{\infty}\frac{x^{s-1}}{\cosh^{2r+1}x}\,dx&=&\frac{1}{2^{2r-1}}\binom{2r}{r}\sum_{k=0}^{\infty}\frac{(-1)^k}{(2k+1)^s}\sum_{j=0}^r(-1)^jt_r(\{2\}^j)(2k+1)^{2j}\\ &=&\frac{1}{2^{2r-1}}\binom{2r}{r}\sum_{j=0}^r(-1)^jt_r(\{2\}^j)\sum_{k=0}^{\infty}\frac{(-1)^k}{(2k+1)^{s-2j}}\\ &=&\frac{1}{2^{2r-1}}\binom{2r}{r}\sum_{j=0}^r(-1)^jt_r(\{2\}^j)\beta(s-2j) \end{eqnarray*}$$
ここで, $\beta(s)$はDirichletのベータ関数である. 上の式において, 解析接続により, $s=2$を代入して,
$$\begin{eqnarray*} \int_0^{\infty}\frac{x}{\cosh^{2r+1}x}\,dx&=&\frac{1}{2^{2r-1}}\binom{2r}{r}\sum_{j=0}^rt_r(\{2\}^j)\beta(2-2j)\\ &=&\frac 1{2^{2r-1}}\binom{2r}r\left(\beta(2)-\sum_{j=0}^{r-1}(-1)^jt_r(\{2\}^{j+1})\beta(-2j)\right) \end{eqnarray*}$$
ここで, Euler数$E_j$を用いて, $\beta(-2j)=\frac{E_{2j}}{2}$と表せることを用いて,
$$\begin{eqnarray*} \int_0^{\infty}\frac{x}{\cosh^{2r+1}x}\,dx&=&\frac 1{2^{2r}}\binom{2r}{r}\left(2\beta(2)-\sum_{j=0}^{r-1}(-1)^jt_r(\{2\}^{j+1})E_{2j}\right) \end{eqnarray*}$$
よって, これより,
$$\begin{eqnarray*} &&\int_0^{\pi/2}\int_x^{\pi/2}\frac{\sin^{2r}x}{\sin^{2r+1}y}\,dydx\\ &=&\frac 1{2^{2r+1}}\binom{2r}{r}\sum_{k=1}^r\frac{2^{2k}}{k(2r-2k+1)\binom{2k}k}+\frac 1{2^{4r}}\binom{2r}{r}^2\left(2\beta(2)-\sum_{j=0}^{r-1}(-1)^jt_r(\{2\}^{j+1})E_{2j}\right) \end{eqnarray*}$$
まとめると, $m$を自然数として,
$$\begin{eqnarray*} I(2r,1)&=&\frac{2^{2r}}{\binom{2r}{r}}\sum_{k=0}^{r-1}\frac{\binom{2k}{k}}{2^{2k}(2r-2k-1)}\\ I(2r+1,1)&=&\frac {2r+1}{2^{2r+1}}\binom{2r}{r}\sum_{k=1}^r\frac{2^{2k}}{k(2r-2k+1)\binom{2k}k}+\frac {2r+1}{2^{4r}}\binom{2r}{r}^2\left(2\beta(2)-\sum_{j=0}^{r-1}(-1)^jt_r(\{2\}^{j+1})E_{2j}\right) \end{eqnarray*}$$
よって, $I(m,1)$をすべて求めることができた.

$$\begin{eqnarray*} \int_0^{\pi/2}J_0(\cos x)\,dx&=&\sum_{n=0}^{\infty}\frac{(-1)^n}{2^{2n}n!^2}\int_0^{\pi/2}\cos^{2n}x\,dx\\ &=&\frac 12\sum_{n=0}^{\infty}\frac{(-1)^n}{2^{2n}n!^2}\frac{\Gamma\left(\frac 12\right)\Gamma\left(n+\frac 12\right)}{\Gamma(n+1)}\\ &=&\frac{\pi}2\sum_{n=0}^{\infty}\frac{(-1)^n\left(\frac 12\right)_n}{2^{2n}n!^3}\\ &=&\frac{\pi}2\sum_{n=0}^{\infty}\frac{1}{n!^2}\binom{2n}n\left(-\frac 1{16}\right)^{n} \end{eqnarray*}$$
一方,
$$\begin{eqnarray*} \left(J_0\left(\frac 12\right)\right)^2&=&\left(\sum_{n=0}^{\infty}\frac{1}{n!^2}\left(-\frac 1{16}\right)^n\right)^2\\ &=&\sum_{n=0}^{\infty}\left(-\frac 1{16}\right)^n\sum_{k=0}^n\frac{1}{k!^2(n-k)!^2}\\ &=&\sum_{n=0}^{\infty}\frac 1{n!^2}\left(-\frac 1{16}\right)^n\sum_{k=0}^n\binom nk^2\\ \end{eqnarray*}$$
ここで, Vandermondeの恒等式より,
$$\begin{eqnarray*} \sum_{k=0}^n\binom nk^2=\binom{2n}n \end{eqnarray*}$$
だから,
$$\begin{eqnarray*} \left(J_0\left(\frac 12\right)\right)^2&=&\sum_{n=0}^{\infty}\frac{1}{n!^2}\binom{2n}n\left(-\frac 1{16}\right)^{n} \end{eqnarray*}$$
よって, 示された.