2つの準同型を同一視する【前編】

$1.$記事の概要

$2$つの線形空間が与えられ，それらの間に線形同型写像があれば，それらの線形空間を同一視することができます．

では，「$2$つの線形写像が」与えられたときに，どのような条件が満たされれば，それらの線形写像を同一視できるでしょうか？実はこの疑問に対する答えが，線形代数でよく見かける$P^{-1}AP$であり，四角い可換図式なのです．

この記事では，$2$つの線形写像，あるいは群準同型や環準同型などを同一視できるための条件について，例を交えて解説します．この記事の内容は，数学のあらゆる分野に現れる重要なものですから，あなたの興味がどの分野にあるかによらず，きっと役に立つことでしょう．ぜひ読んでみてください！

みなさんきっとお忙しいでしょうから，最後まで読まなくてもいいように重要な内容ほど最初の方に載せています．冒頭の少しだけでも目を通してみてください．

定義$\to$色々な分野の具体例$\to$圏論による整理，という順番に記述していきます．

後編はここです： 記事「2つの準同型を同一視する【後編】」

$2.$準同型を同一視するための条件

2.1 射同型の定義

いきなり本題から入りましょう．

実は$f,g$が射同型のとき，準同型や写像としての性質が同じになります．例えば一方が全射なら他方も全射になるとか，核どうしが同型になるなどです．

(定義$1$に出てくる用語や記号の使い方は，この記事だけの用語・記号であり，一般的なものではないので注意してください．また，「射が同型(同型写像)であること」と「$2$つの射が射同型の関係にあること」とはもちろん異なる概念なので，注意してください．前者は1つの射が持つ性質，後者は2つの射の関係を表す語です．この区別のためにこの記事では射同型という独自の用語を用いました．)

少し説明します．

まず「射」とは，この記事では準同型とか写像のことだと思っていいです．

「可換図式」とは，どの経路で射を合成しても，合成した結果が同じになるような図式のことです．定義$1$に出てくる図式について言えば，$g\circ s=t\circ f$が成り立つことが，これが可換図式であるための必要十分条件です．

なので結局，定義$1$は，「$t\circ f=g\circ s$で$s,t$が同型のとき，$f$と$g$は射同型ということにするよ」ということを述べています．

2.2 定義と同値な条件

定義$1$と同値な条件を述べます．

軽く示しておくと，$g\circ s=t\circ f$のとき，両辺の右端に$s^{-1}$を合成することで$g=t\circ f\circ s^{-1}$が得られます．逆に$g=t\circ f\circ s^{-1}$とすると，両辺の右端に$s$を合成することで$g\circ s=t\circ f$が得られますね．

数学をしていて射の合成についての$g=t\circ f\circ s^{-1}$という関係式が出てきたら($s,t$が同型なら)命題$1$により，射同型チャンスと見ることができます．(もちろん定義$1$の可換図式を見た時も射同型チャンスです．)このとき，「$f,g$は同一視できる，色々の性質を共にするはずだ！」と思ってよいです．

また命題$1$とほぼ同じことですが，次の形でも頭に入れておくといいでしょう：

要するに，射$f$が同型$s,t$で挟まれているのを見たら，射同型チャンスということです．このとき$f$と$t\circ f \circ s$は同一視できます．(さらに言うと，$s$や$t$が$\text{id}$の場合を考えることで，$f$と$t\circ f$，あるいは$f$と$f\circ s$とを同一視できることも頭に入れておくといいでしょう．)

$3.$様々な具体例を見てみよう

3.1 線形代数

この記事では行列はそのまま線形写像とみなします．

3.1.1 対角化

$A:=\dfrac{1}{7}\begin{pmatrix} 15&-3\\ -2&20 \end{pmatrix}, P:=\dfrac{1}{7}\begin{pmatrix}2&1\\-1&3\end{pmatrix}, \Lambda:=\begin{pmatrix}2&0\\0&3\end{pmatrix}$という行列を考え，それぞれ線形写像$\mathbb{R}^2\to \mathbb{R}^2$とみなします．すると，計算により$\Lambda P=PA$がわかり，また$P$は線形同型写像(正則行列)であるため，線形写像のなす図式

は定義$1$の条件を満たし，$A\overset{(P,P)}{\cong} \Lambda$が得られます．

ここで，$A$はパッと見ではどんな線形写像なのかわかりません．一方，$\Lambda$は$x$成分を$2$倍，$y$成分を$3$倍にするだけの簡単な線形写像ですね($(x,y)\mapsto (2x,3y)$)．射同型$A\cong \Lambda$は，「よくわからない$A$は，実はわかりやすい$\Lambda$と同一視できるよ」ということを教えてくれています．
さて$\Lambda$は$A$の対角化になっています．実際$\Lambda P=PA$の両辺に$P^{-1}$を右からかけると$\Lambda=PAP^{-1}$というよく見る形になりますね．行列の対角化には，よくわからない行列をわかりやすい対角行列と同一視することで，わからなかった行列のことをわかることができるという意味があるのです．

(もう少し詳しく見ると，$P^{-1}=\begin{pmatrix}3&-1\\1&2\end{pmatrix}$の$2$つの列ベクトル$v_1=\begin{pmatrix}3\\1\end{pmatrix},v_2=\begin{pmatrix}-1\\2\end{pmatrix}$を取ると，$\{v_1,v_2\}$は$\mathbb{R}^2$の基底であり，計算により$Av_1=2v_1,Av_2=3v_2$となっていることがわかります．よって$A$は$v_1$方向に$2$倍，$v_2$方向に$3$倍に伸ばすような線形写像になっています．これは対角行列$\Lambda$が$e_1:=\begin{pmatrix}1\\0\end{pmatrix}$方向に$2$倍，$e_2:=\begin{pmatrix}0\\1\end{pmatrix}$方向に$3$倍に伸ばすような線形写像になっていることと対応しています．$A$と$\Lambda$とは射同型なだけあって，確かに似ていますね！)

$A$と$\Lambda$は似ている

3.1.2 掃き出し

行列$B:=\begin{pmatrix}2&2&4\\1&2&5\end{pmatrix}$に対して掃き出しを行い，階段行列にすることを考えましょう．次のようになります：
$B=\begin{pmatrix}2&2&4\\1&2&5\end{pmatrix}\overset{1\text{行目}\times 1/2}{\longrightarrow} B_1:=\begin{pmatrix}1&1&2\\1&2&5\end{pmatrix}\overset{2\text{行目}-1\text{行目}}{\longrightarrow}B_2:=\begin{pmatrix}1&1&2\\0&1&3\end{pmatrix}\overset{1\text{行目}-2\text{行目}}{\longrightarrow} B_3:=\begin{pmatrix}1&0&-1\\0&1&3\end{pmatrix}.$

$3$回行われた操作はそれぞれ正則行列$T_1:=\begin{pmatrix}1/2&0\\0&1\end{pmatrix},T_2:=\begin{pmatrix}1&0\\-1&1\end{pmatrix},T_3:=\begin{pmatrix}1&-1\\0&1\end{pmatrix}$を左からかけることに相当し，次の可換図式が成立します：

ただし，左の縦の射の二重線は恒等写像を表します．
$B\overset{(\text{id},T_1)}{\cong}B_1\overset{(\text{id},T_2)}{\cong}B_2\overset{(\text{id},T_3)}{\cong}B_3$と次々に射同型な射に移っていき，もとの行列と階段行列との射同型$B\cong B_3$が得られています．

実際，図式の$1$番外側が次のように定義$1$の条件を満たす可換図式になっています：

$B$のランクなどはパッと見ではわかりませんが，階段行列$B_3$のランクなどはすぐにわかります．与えられた行列を，射同型，射同型...で変換していって最終的に階段行列というわかりやすい行列に変換するというのが，掃き出しという操作なのです．

3.2 集合の写像

3.2.1 書き換え

この項で説明する書き換えという概念が射同型を理解する上でめちゃくちゃ大事です．(書き換えという用語も必ずしも一般的なものではないかもしれません．私がそう呼んでいるだけです．)
$4$つの集合$X_1,X_2,Y_1,Y_2$を次のように定めます：
$X_1=\{a,b,c,d,e\},$
$X_2=\{A,B,C,D,E\},$
$Y_1=\{\text{あ },\text{い},\text{う }\},$
$Y_2=\{\text{ア },\text{イ},\text{ウ }\}.$

写像$f_i:X_i\to Y_i(i=1,2),s:X_1\to X_2,t:Y_1\to Y_2$を次のように定めます：
唐突な手書き
$s,t$は全単射であり，次の可換図式が成立します：

したがって$f_1\overset{(s,t)}{\cong}f_2$です．ここで$f_1$と$f_2$をよく比べてみてください．

$f_1$の対応表を，$s,t$を用いて書き換えてみましょう．つまり，$s$は小文字を大文字に変換する写像なので$f_1$の始域の小文字を大文字に書き換え，また，$t$はひらがなをカタカナに変換する写像なので，$f_1$の終域のひらがなをカタカナに書き換えてみましょう．すると，
$s,t$を用いて$f_1$の対応表を書き換えた

$f_2$の対応表になりました！
これはめちゃくちゃ重要な事実です．一般に写像の射同型$f_1\overset{(s,t)}{\cong}f_2$があれば，$f_1$を$s,t$によって書き換えたものが$f_2$になっているのです！

ここで，$f_2=t\circ f_1 \circ s^{-1}$なので，次のように表現することもできます：

射同型な$2$つの射は書き換えたものに過ぎないとわかると，色々な性質を共にすることも納得できるのではないでしょうか．

さらに，グラフについても書き換えになっていることを見てみましょう．
先ほど定義した$f_1,f_2$のグラフは次のようになっています：
$f_1,f_2$のグラフ
$f_1$のグラフを，$s,t$を用いて書き換えてみましょう．つまり$s$により始域の小文字を大文字に，$t$により終域のひらがなをカタカナに書き換えます．すると次のようになります：
$f_1$のグラフを$s,t$で書き換えた
$f_1$のグラフが書き換えによって$f_2$のグラフになりました！一般に写像の射同型$f_1\overset{(s,t)}{\cong}f_2$が成り立つとき，$f_1$のグラフを$s,t$により書き換えたものが，$f_2$のグラフになっているのです．

3.2.2 単射と全射

$A,B,C,D$は集合で，写像のなす可換図式

があり，縦の$2$本の射$s,t$が全単射であるとします．(よって$f\cong g.$)
$f$と$g$とは射同型なので，$f,g$の一方が単射なら，他方も単射であってほしいですよね．同様に，一方が全射なら，他方も全射であってほしいです．実際これらのことは成立します．

(証明は省略しますが，$f,g$は3.2.1項で見たように互いに書き換えたものになっていることを考えれば，これらの命題は当たり前に思えるのではないでしょうか？)

3.2.3 みなし部分集合と本当の部分集合

集合$A,B$と単射$f:A\to B$があるときに，この単射$f$をもって$A$を$B$の部分集合とみなすことが数学においてはよくあります．ではこのとき，$B$の本当の部分集合であって$A$に対応するものは何でしょうか？

$f$と$A$を使って$B$の部分集合を作ろうと思ったら，自然に像$f(A)$を思いつくと思います．実際$i:f(A)\to B,b\mapsto b$を包含写像とすると，次の図式は可換になります：

ここで右の縦の射の二重線は恒等写像$\text{id}_B:B\to B,b\mapsto b$を表します．また$\overset{\sim}{f}$は$f$の終域を制限したものです：
\begin{array}{rccc} \overset{\sim}{f}:&A&\longrightarrow&f(A)\\ &a&\longmapsto&f(a) \end{array}
よって$f\overset{(\overset{\sim}{f},\text{id}_B)}{\cong}i$となり，単射$f$は包含写像$i$と同一視できることがわかりました．$A$は$f(A)$に対応し，単射$f:A\to B$は包含写像$i:f(A)\to B$と対応します．

(この項で見たことのさらなる具体例を3.5.2項に載せています．)

3.3 グラフの平行移動

3.3.1 放物線を平行移動する

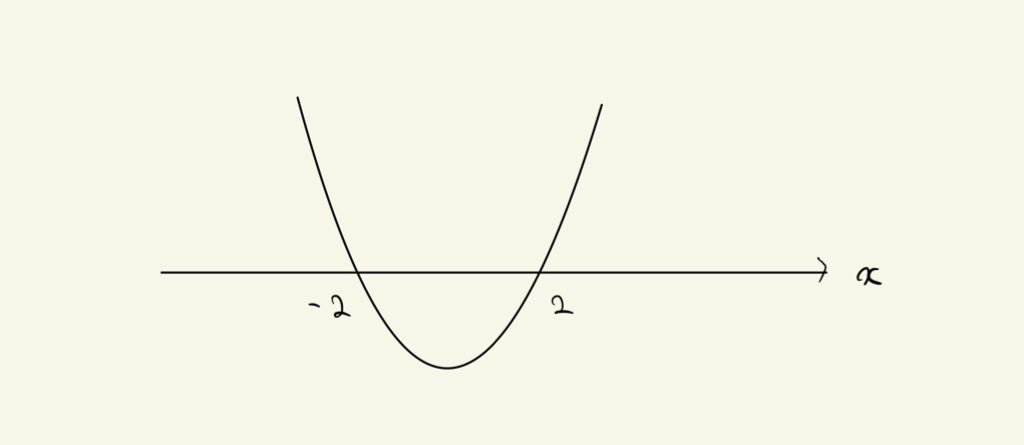
関数$f:\mathbb{R}\to \mathbb{R}$を$f(x)=x^2-4$で定めます．$y=f(x)$のグラフは次のとおりです：
$y=f(x)=x^2-4$の大雑把なグラフ
このグラフを$x$軸方向に$+1$平行移動させることを考えましょう．
$x$軸方向の平行移動を表す関数$s:\mathbb{R}\to \mathbb{R}$を$s(x)=x+1$で定めます．$s$は全単射です．次のような図式を考えましょう：

もしこの図式を可換にする$g$があれば，$f\overset{(s,\text{id}_{\mathbb{R}})}{\cong}g$となり，$f$は$s$による$x$軸方向の平行移動で$g$に対応すると言えそうです．なお右の縦の射が恒等写像なのは，$y$軸方向へは動かさないからです．$g$はどのように定めればいいでしょうか？インスピレーションが必要でしょうか？

いえいえ，$g$は計算により導き出せます．命題$1$により，$g=\text{id}_{\mathbb{R}}\circ f\circ s^{-1}$と定めればいいです．計算してみると，
\begin{aligned} g(x)&=\text{id}_{\mathbb{R}}\circ f\circ s^{-1}(x)\\ &=\text{id}_{\mathbb{R}}\circ f(x-1)\\ &=\text{id}_{\mathbb{R}}((x-1)^2-4)\\ &=(x-1)^2-4 \end{aligned}
となります．この$g$により上の図式は可換図式になり，$f\cong g$です．

$x$軸方向の$+1$の平行移動により，$f$は$g$に対応することがわかりました．実際グラフを描くと，$y=f(x)$のグラフを$x$軸方向に$+1$平行移動させたものが$y=g(x)$のグラフになることがわかります．

(よく，次のような疑問を見かけます：
「どうして$y=f(x)$のグラフを$x$軸方向に$+$$1$平行移動したグラフが，$y=f(x+1)$ではなく$y=f(x$$-$$1)$になるの？」
この疑問に対する$1$つの回答として次のようなものがありうると思います：
「上の図式を可換にするためには，$g\circ s=\text{id}\circ f=f$とならなくてはならないが，$s$で$+1$される分を$g$で$-1$しないと合わなくなるから」
実際$g(x)=f(x-1)$と定めることで，$g(s(x))=g(x+1)=f((x-1)+1)=f(x)$となりますね．)

さて，3.2.1項で見たことと同じことをしてみましょう．
$f,g$の対応表は次の通りです：
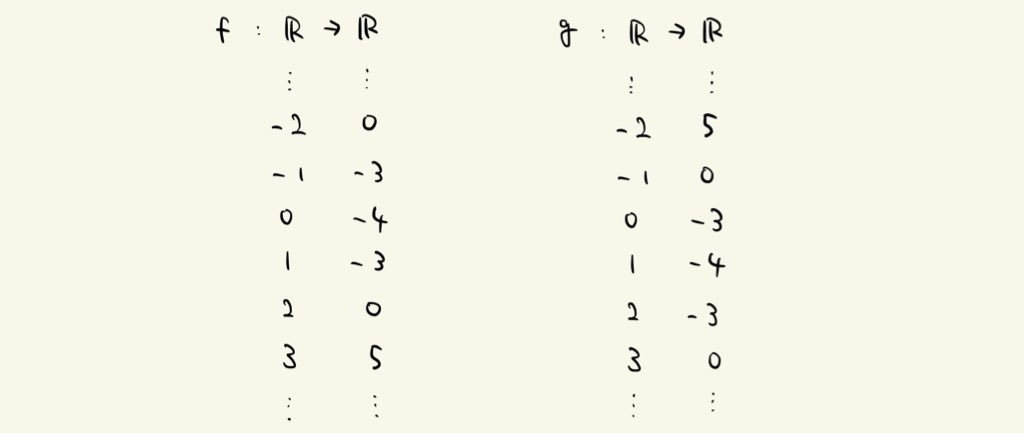もちろん一部だけ
$f$の対応表を，$s,\text{id}_{\mathbb{R}}$で書き換えましょう．つまり$s$により始域の数字を$+1$します．(終域は$\text{id}_{\mathbb{R}}$で書き換える…つまり何もしません．)すると次のようになります：
$s,\text{id}_{\mathbb{R}}$で書き換えた
$g$の対応表になりました！

また，$f$のグラフは次の通りです：
再掲
やはり始域の数字を$s$によって書き換えましょう．すると次のようになります：
書き換えた
$g(x)=(x-1)^2-1$のグラフになりました！
3.2.1項で見たことがここでも確認されました．

これで前編を終わります．後編では群論，環論，環上の加群に関する具体例を見たあと，定義$1$を圏論を使って整理します．

後編はこちら： 記事「2つの準同型を同一視する【後編】」