三色関数(col関数)に幾何学的意味を与えるよ!
三色関数に幾何学的意味を与えるよ!
概要説明
今回の記事は微分や三角関数やマクローリン展開、複素関数、線形代数あたりの知識をお持ちの方を対象としております。それらについての解説からはじめてしまうとなかなか本題に入れないため、本記事ではいつもよりやや高度なお話が多めかもしれません。。何卒、ご了承くださいませ><
さて、twitter 上の数学クラスタさんの間で「三色関数」なるものがプチブームとなっているようです。
$$\begin{align}
\mathrm{red}~x=&\frac{e^x+e^{\omega x}+e^{\omega^2 x}}3\\
\mathrm{grn}~x=&\frac{e^x+\omega^2 e^{\omega x}+\omega e^{\omega^2 x}}3\\
\mathrm{blu}~x=&\frac{e^x+\omega e^{\omega x}+\omega^2 e^{\omega^2 x}}3\\
\end{align}$$
(本記事内では、$\omega$ を $1$ の原始三乗根として扱います)
三色関数というのは Melvilleさん が提唱された関数とのことで、なかなかステキなネーミングセンスだと思いました! もちろん、$n$階微分して元に戻る関数について考えたことがある方であれば同質のものを見つけたよって方もおられるかもしれませんが、やはり命名って大事だなと感じた次第です。
かくいう私も「周階導関数($n$階微分して元に戻る関数)を線形結合的に表す」というアイデアから、その元として「$\exp_s$関数(skipped exponential 関数)」なるものを得ておりまして、どういうものかといいますと、
$$\begin{align}
\exp_sx&=\sum_{k=0}^\infty\frac{x^{ks}}{(ks)!}\\
\exp_3x&=\sum_{k=0}^\infty\frac{x^{3k}}{(3k)!}=\mathrm{red}~x\\
\exp''_3x&=\sum_{k=0}^\infty\frac{x^{3k+1}}{(3k+1)!}=\mathrm{grn}~x\\
\exp'_3x&=\sum_{k=0}^\infty\frac{x^{3k+2}}{(3k+2)!}=\mathrm{blu}~x\\
\end{align}$$
という感じで三色関数と対応しております。($'$ は導関数であることを示しています。$\exp'_zx=(\exp_zx)'$、$\exp''_zx=(\exp_zx)''$)
私の場合はガラパゴ数学をベースとしているもので、このような解析的に得られた関数の先にも幾何イメージを視ているのですが、それについて詳細説明に入る前にまずは概要からざっくり紹介していきましょう。
「極座標形式の複素数」と「$1$ と $z$ を基底の元とする斜交座標形式の複素数」を相互変換する式
$$\quad\quad\large e^{xz}=\left(\cos_zx\right)+z\left(\sin_zx\right)$$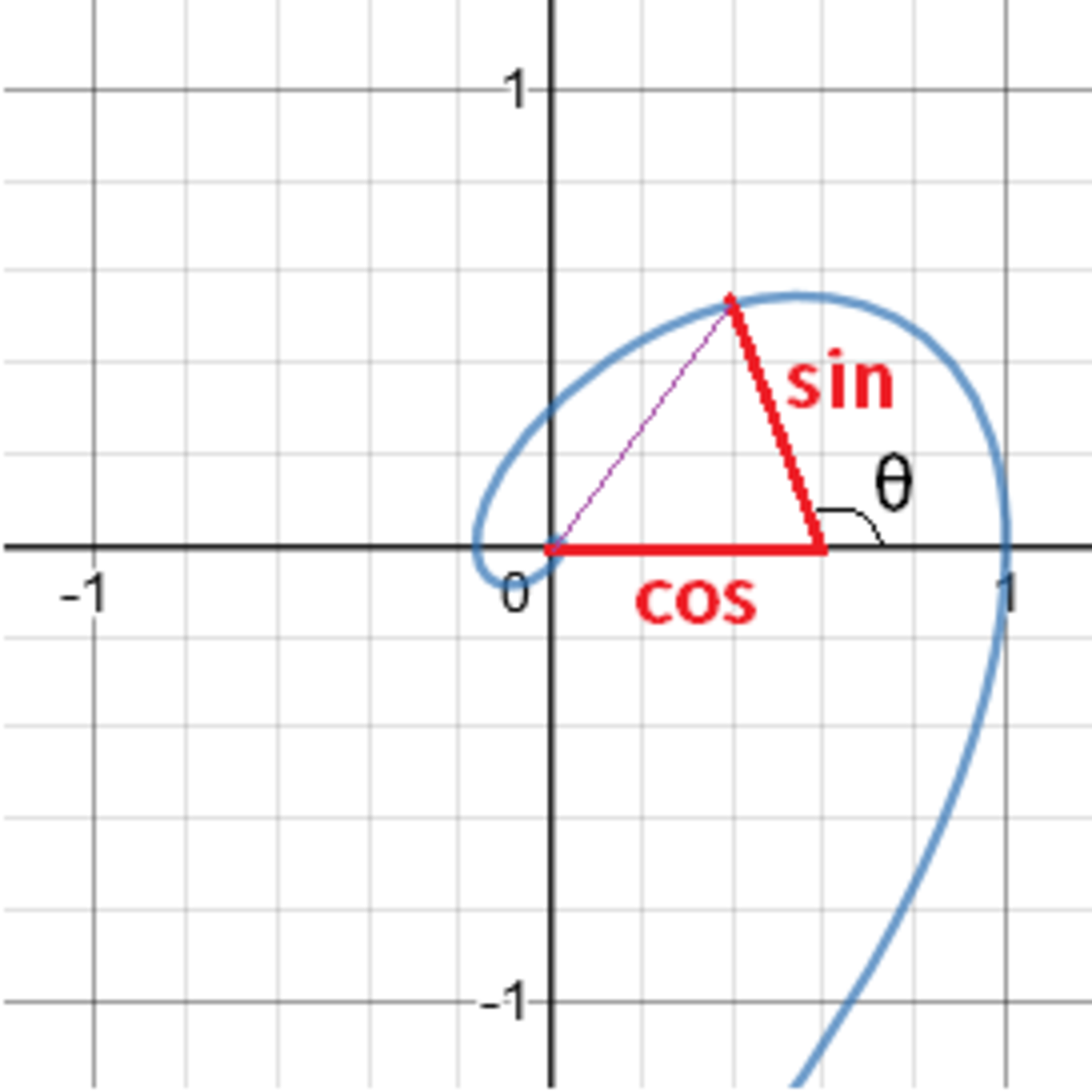
こちらは見ての通り、オイラーの公式の斜交座標バージョンです。この $\cos_zx$ と $\sin_zx$ は いわゆる普通の三角関数を斜交座標系へと純粋拡張させたもので ガラパゴ三角関数 と呼ばせていただいているものなのですが、本記事においては「極座標形式と斜交座標形式の関係式」という視点にご注目いただければ理解しやすくなるかと思います。(こうみると、やはり $\cos$ や $\sin$ は円関数ではなく「三角」関数ですね。)
さて、これと三色関数や$\exp_s$関数との関係はといいますと$\cdots$
| $\exp_s$関数 | 基底 | 基底の第$1$元成分(実部) | 基底の第$2$元成分(虚部) |
|---|---|---|---|
| $\exp_1x=\exp x$ | $\{1,~z=e^{\frac{2\pi}1i}=1\}$ | $\cos_zx=(1-x)e^x$ | $\sin_zx=xe^x$ |
| $\exp_2x=\cosh x$ $\exp'_2x=\sinh x$ | $\{1,~z=e^{\frac{2\pi}2i}=-1\}$ | $\cos_zx=(1+x)e^{-x}$ | $\sin_zx=xe^{-x}$ |
| $\exp_3x=\mathrm{red}~x$ $\exp''_3x=\mathrm{grn}~x$ $\exp'_3x=\mathrm{blu}~x$ | $\{1,~z=e^{\frac{2\pi}3i}=\omega\}$ $\{1,~z=e^{\frac{4\pi}3i}=\omega^2\}$ | $\begin{align}\cos_zx=&\exp_3x-\exp'_3x\\=&\mathrm{red}~x-\mathrm{blu}~x\end{align}$ | $\begin{align}\sin_zx=&\exp''_3x-\exp'_3x\\=&\mathrm{grn}~x-\mathrm{blu}~x\end{align}$ |
| $\exp_4x$ $\exp'''_4x$ $\exp''_4x$ $\exp'_4x$ | $\{1,~z=e^{\frac{2\pi}4i}=+i\}$ $\{1,~z=e^{\frac{6\pi}4i}=-i\}$ | $\begin{align}\cos_zx=&\exp_4x-\exp''_4x\\=&\cos x\end{align}$ | $\begin{align}\sin_zx=&\exp'''_4x-\exp'_4x\\=&\sin x\end{align}$ |
| $\exp_5x$ $\exp''''_5x$ $\exp'''_5x$ $\exp''_5x$ $\exp'_5x$ | $\{1,~z=e^{\frac{2\pi}5i}=\zeta_5\}$ $\{1,~z=e^{\frac{8\pi}5i}=\zeta_5^4\}$ | $\begin{align}\cos_zx=&\exp_5x-\exp'''_5x\\&+\phi'\exp'_5x-\phi'\exp''_5x\end{align}$$$\quad\quad\textstyle\left(\phi'=\phi^{-1}=\frac{\sqrt5-1}2\right)$$ | $\begin{align}\sin_zx=&\exp''''_5x-\exp'_5x\\&+\phi'\exp'''_5x-\phi'\exp''_5x\end{align}$$$\quad\quad\textstyle\left(\phi'=\phi^{-1}=\frac{\sqrt5-1}2\right)$$ |
| $\exp_5x$ $\exp''''_5x$ $\exp'''_5x$ $\exp''_5x$ $\exp'_5x$ | $\{1,~z=e^{\frac{4\pi}5i}=\zeta_5^2\}$ $\{1,~z=e^{\frac{6\pi}5i}=\zeta_5^3\}$ | $\begin{align}\cos_zx=&\exp_5x-\exp'''_5x\\&+\phi\exp''_5x-\phi\exp'_5x\end{align}$$$\quad\quad\textstyle\left(\phi=\frac{\sqrt5+1}2\right)$$ | $\begin{align}\sin_zx=&\exp''''_5x-\exp'_5x\\&+\phi\exp''_5x-\phi\exp'''_5x\end{align}$$$\quad\quad\textstyle\left(\phi=\frac{\sqrt5+1}2\right)$$ |
| $\vdots$ | $\vdots$ | $\vdots$ | $\vdots$ |
なんとなくイメージは掴めましたでしょうか。が、問題はこれらの式を一体どうやって求めたのかというところですよね。それこそが本記事のメイントピックですので、これより詳細解説に入らせていただくとしましょう。
$n$階微分すると元に戻る関数
さて、先述しました $n$階の周階導関数。一般形については様々な形で表現されるかとは思いますが、私の得た式は以下の通りです。
$$f(x)=\sum_{k=0}^\infty\sum_{m=0}^{n-1}\frac{a_m\cdotp x^{kn+m}}{(kn+m)!}$$
実際に微分してみるとわかると思いますが、いずれの項の分母も $x$ の次数の階乗となっていて分子の $a_m$ のみが微分した階数分だけズレていきます。これが $a_0,~a_1,~\cdots,~a_{n-1}$ のループとなっているため $n$ 階微分で元の関数に戻る、という仕組みですね。こういう形の関数を「$n$階の周階導関数」と呼ぶことにし、以後は
$$[a_0,~a_1,~a_2,~\cdots,~a_{n-1}]$$
と簡略表記するものとします。こうすると、微分してズレる様は次のように表せるのです。
$[a_0,~a_1,~a_2,~\cdots,~a_{n-1}]'=[a_1,~a_2,~\cdots,~a_{n-1},~a_0]$
$[a_0,~a_1,~a_2,~\cdots,~a_{n-1}]''=[a_2,~\cdots,~a_{n-1},~a_0,~a_1]$
(これらの呼称や記法は一般的なものではなく、説明の便宜上用いているものですのでご了承ください。)
では、一般的によく知られている $n$階の周階導関数の例をいくつかみてみます。
| $n$ | 関数 | 簡略表記 | マクローリン展開形 |
|---|---|---|---|
| $1$ | $\exp~x=\exp_1x$ | $[1]$ | $$\sum_{k=0}^\infty\frac{x^k}{k!}$$ |
| $2$ | $\cosh x=\exp_2x$ | $[1,0]$ | $$\sum_{k=0}^\infty\frac{x^{2k}}{(2k)!}$$ |
| $2$ | $\sinh x=\exp'_2x$ | $[0,1]$ | $$\sum_{k=0}^\infty\frac{x^{2k+1}}{(2k+1)!}=\left(\sum_{k=0}^\infty\frac{x^{2k}}{(2k)!}\right)'$$ |
| $3$ | $\mathrm{red}~x=\exp_3x$ | $[1,0,0]$ | $$\sum_{k=0}^\infty\frac{x^{3k}}{(3k)!}$$ |
| $3$ | $\mathrm{grn}~x=\exp''_3x$ | $[0,1,0]$ | $$\sum_{k=0}^\infty\frac{x^{3k+1}}{(3k+1)!}=\left(\sum_{k=0}^\infty\frac{x^{3k}}{(3k)!}\right)''$$ |
| $3$ | $\mathrm{blu}~x=\exp'_3x$ | $[0,0,1]$ | $$\sum_{k=0}^\infty\frac{x^{3k+2}}{(3k+2)!}=\left(\sum_{k=0}^\infty\frac{x^{3k}}{(3k)!}\right)'$$ |
| $4$ | $\cos x=\exp_4x-\exp''_4x$ | $[1,0,-1,0]$ | $$\sum_{k=0}^\infty\frac{(-1)^k\cdotp x^{2k}}{(2k)!}=\left(\sum_{k=0}^\infty\frac{x^{4k}}{(4k)!}\right)-\left(\sum_{k=0}^\infty\frac{x^{4k}}{(4k)!}\right)''$$ |
| $4$ | $\sin x=\exp'''_4x-\exp'_4x$ | $[0,1,0,-1]$ | $$\sum_{k=0}^\infty\frac{(-1)^k\cdotp x^{2k+1}}{(2k+1)!}=\left(\sum_{k=0}^\infty\frac{x^{4k}}{(4k)!}\right)'''-\left(\sum_{k=0}^\infty\frac{x^{4k}}{(4k)!}\right)'$$ |
ここで、幾何学的分野に用いられる $\cos$ と $\sin$ のマクローリン展開形がやや異質(?)な形になっていることにお気づきでしょうか。これの意味するところは、先程の座標変換式を考えると視えてきます。
$$e^{xi}=(\cos x)+i(\sin x)$$
左辺は $\displaystyle e^{xi}=\sum_{k=0}^\infty\frac{i^k\cdotp x^k}{k!}$ ですので、簡略表記すると $[1,i,-1,-i]$ ですね。対する右辺は $1$ と $i$ を基底の元とする一次結合の形になっているわけですから、
$\begin{array}{cr}
&1&0&-1&0\\
+&0&i&0&-i\\
\hline
&1&i&-1&-i
\end{array}$ → $[1,i,-1,-i]=[1,0,-1,0]+i[0,1,0,-1]$
というように分離することで $\cos x$ と $\sin x$ の簡略表記を得ることができます。さらに周階導関数は微分すると係数がズレますので
$$\begin{cases}
[1,0,-1,0]=[1,0,0,0]-[0,0,1,0]=[1,0,0,0]-[1,0,0,0]''\\[4pt]
[0,1,0,-1]=[0,1,0,0]-[0,0,0,1]=[1,0,0,0]'''-[1,0,0,0]'\\
\end{cases}$$
とも表せます。この形こそがまさに異質(?)の正体というわけです。
$$\begin{cases}
\cos x=\exp_4x-\exp''_4x\\[4pt]
\sin x=\exp'''_4x-\exp'_4x\\
\end{cases}$$
これ、同じことを三色関数でもやってみたくなりませんか? では、早速試してみましょう。
三色関数に幾何学的意味を
$$e^{x\omega}=(\cos_\omega x)+\omega(\sin_\omega x)$$
左辺の簡略表記は $[1,\omega,\omega^2]$ なのですが、おやおや、$1$ と $\omega$ を基底の元としたいのに、$\omega^2$ という元が出てきてしまいました。単純に考えるなら
$$[1,\omega,\omega^2]=[1,0,0]+\omega[0,1,0]+\omega^2[0,0,1]$$
すなわち
$$\begin{align}
e^{x\omega}=&(\exp_3x)+\omega(\exp'’_3x)+\omega^2(\exp'_3x)\\
=&(\mathrm{red}~x)+\omega(\mathrm{grn}~x)+\omega^2(\mathrm{blu}~x)
\end{align}$$
としてももちろんよいのですが、複素平面というのは二次元平面上ですから二つの独立元で表せるはずですね。ここでは $\omega^2$ も $1$ と$\omega$ を基底の元とする座標で表現したいところ。実際、$1+\omega+\omega^2=0$ より $\omega^2=-1-\omega$ と表わせますので、
$\begin{array}{cr}
&1&0&-1~\\
+&0&\omega&-\omega~\\
\hline
&1&\omega&\omega^2
\end{array}$ → $[1,\omega,\omega^2]=[1,0,-1]+\omega[0,1,-1]$
$$\begin{cases}
[1,0,-1]=[1,0,0]-[0,0,1]=[1,0,0]-[1,0,0]'\\[4pt]
[0,1,-1]=[0,1,0]-[0,0,1]=[1,0,0]''-[1,0,0]'\\
\end{cases}$$
$$\therefore~\begin{cases}
\cos_\omega x=\exp_3x-\exp'_3x=\mathrm{red}~x-\mathrm{blu}~x\\
\sin_\omega x=\exp''_3x-\exp'_3x=\mathrm{grn}~x-\mathrm{blu}~x\\
\end{cases}$$
$$e^{x\omega}=(\cos_\omega x)+\omega(\sin_\omega x)=(\mathrm{red}~x-\mathrm{blu}~x)+\omega(\mathrm{grn}~x-\mathrm{blu}~x)$$
と、このように三色関数を組み合わせることで $e^{x\omega}$ を $1$ と $\omega$ を基底の元とする斜交座標形式で表現することができました。
ところでこれ、 $\omega$ を $1$ と$\omega^2$ を基底の元とする座標系で表すこともできたはず。すなわち、
$$e^{x\omega^2}=(\cos_{\omega^2} x)+\omega^2(\sin_{\omega^2} x)$$
としていたらどうなっていたでしょうか。面白いことに、実はこうなるんです。
$\begin{array}{cr}
&1&0&-1~~\\
+&0&\omega^2&-\omega^2\\
\hline
&1&\omega^2&\omega~~\\
\end{array}$ → $[1,\omega^2,\omega]=[1,0,-1]+\omega^2[0,1,-1]$
$$\begin{cases}
[1,0,-1]=[1,0,0]-[0,0,1]=[1,0,0]-[1,0,0]'\\[4pt]
[0,1,-1]=[0,1,0]-[0,0,1]=[1,0,0]''-[1,0,0]'\\
\end{cases}$$
$$\therefore~\begin{cases}
\cos_{\omega^2}x=\exp_3x-\exp'_3x=\mathrm{red}~x-\mathrm{blu}~x\\
\sin_{\omega^2}x=\exp''_3x-\exp'_3x=\mathrm{grn}~x-\mathrm{blu}~x\\
\end{cases}$$
$$e^{x\omega^2}=(\cos_{\omega^2}x)+\omega^2(\sin_{\omega^2}x)=(\mathrm{red}~x-\mathrm{blu}~x)+\omega^2(\mathrm{grn}~x-\mathrm{blu}~x)$$
ナント、$e^{x\omega}$ と全く同形になりました。それもそのはず、$\omega$ と $\omega^2$ は複素共役の関係つまり複素平面上の実軸で鏡映対称のため、幾何イメージ的にはむしろ同じになって当然といえるでしょう。
さらに高階になったらどうなるの?
ここまで、$z=e^{\frac{2\pi}3i}=\omega$ と $z=e^{\frac{2\pi}4i}=i$ についてみてきましたので、お次は $z=e^{\frac{2\pi}5i}=\zeta_5$ についてみてみます。
$$e^{xz}=(\cos_zx)+z(\sin_zx)$$
高階になっても、やることはこれまでと全く同じ。ネックとなるのは三色関数のときにもあった「$1$ と $z$ を基底の元とする斜交座標形式で任意の $z^n$ を 表現する」という問題の解決でしょうか。これについては ガラパゴ累乗定理 というのを用いれば次のように解決できちゃいます。
$l=z\cdotp\overline{z}=|z|^2=|\zeta_5|^2=1$
$r=z+\overline{z}=2\mathrm{Re}~z=2\cos\left(\mathrm{Arg}~\zeta_5\right)=2\cos\frac{2\pi}5=\frac{\sqrt5-1}2=\phi^{-1}=\phi'$ として
$S_0=0$、$S_1=1$、$S_n=-(S_{n-2})l+(S_{n-1})r$ からの $z^n=-l(S_{n-1})+(S_n)z$ より
$$\begin{cases} z^0=1+0z&=1+0\\ z^1=0+1z&=0+\zeta_5\\ z^2=-l+rz&=-1+\phi'\zeta_5\\ z^3=-rl+(r^2-l)z&=-\phi'-\phi'\zeta_5\\ z^4=-(r^2-l)l+(r^3-2rl)z&=-\phi'-\zeta_5\\ \end{cases}$$
$\begin{array}{cr} &1&0~&-1~~~&-\phi'~~~&\phi'\\ +&0&\zeta_5&\phi'\zeta_5&-\phi'\zeta_5&-\zeta_5\\ \hline &1&\zeta_5&\zeta_5^2&\zeta_5^3&\zeta_5^4\\ \end{array}$ → $[1,\zeta_5,\zeta_5^2,\zeta_5^3,\zeta_5^4]=[1,0,-1,-\phi',\phi']+\zeta_5[0,1,\phi',-\phi',-1]$
$$\begin{cases} [1,0,-1,-\phi',\phi']=[1,0,0,0,0]-[0,0,1,0,0]-\phi'[0,0,0,1,0]+\phi'[0,0,0,0,1]\\[4pt] [0,1,\phi',-\phi',-1]=[0,1,0,0,0]+\phi'[0,0,1,0,0]'-\phi'[0,0,0,1,0]-[0,0,0,0,1] \end{cases}$$
$$\therefore~\begin{cases} \cos_zx=\exp_5x-\exp'''_5x-\phi'\exp''_5x+\phi'\exp'_5x\\[4pt] \sin_zx=\exp''''_5x+\phi'\exp'''_5x-\phi'\exp''_5x-\exp'_5x \end{cases}$$
ガラパゴ累乗定理に関する解説については本題から外れてしまうためここでは省略させていただきますが(気になる方は数学を愛する会wikiの「 ガラパゴ累乗定理 」やmathlog記事「 フィボナッチ数とリュカ数とガラパゴ数学 」を参照してね)、$l=z\cdotp\overline z=|z|^2$ と $r=z+\overline z=2\mathrm{Re}~z$ さえ求められれば任意の $z$ に対する $\cos_zx$ と $\sin_zx$ の簡略表記の数列、ひいてはマクローリン展開形が分かるという点がポイントです。
例えば $z=e^{\frac{2\pi}{10}i}$ のとき $2\cos\frac{2\pi}{10}=\frac{1+\sqrt5}2=\phi$ ですので、黄金数大好きな方はこの場合の $\cos_zx$ と $\sin_zx$ のマクローリン展開形を求めてみると面白いかも(*´艸`*)
とりま、「任意の $z$ に対して $\cos_zx$ と $\sin_zx$ を簡略表記したときの数列」が「$1$ と $z$ を基底の元とする座標系で $z^n$ を表したときの実成分と $z$ 成分」にそれぞれ一致するよってことをなんとなくでも掴んでいただければ御の字でございます。
ちなみに、$\sin_zx$ 側の数列はガラパゴ累乗定理の性質上 $z$ を生成元とする 第1種ガラパゴ数列 $a_n=\frac{\mathrm{Im}~z^n}{\mathrm{Im}~z}$ に一致しており、特に $z$ が非実数の場合の一般式は次のようにも表せますよということを付記しておきますね。
$$\begin{align} e^{xz}=&\left(\cos_zx\right)+z\left(\sin_zx\right)\\ =&\left[\sum_{k=0}^\infty\sum_{m=0}^{n-1}\frac{\left(\frac{-|z|^2\mathrm{Im}~z^{m-1}}{\mathrm{Im}~z}\right)\cdotp x^{kn+m}}{(kn+m)!}\right]+z\left[\sum_{k=0}^\infty\sum_{m=0}^{n-1}\frac{\left(\frac{\mathrm{Im}~z^m}{\mathrm{Im}~z}\right)\cdotp x^{kn+m}}{(kn+m)!}\right] \end{align}$$
逆に、$1$階や$2$階のときは?
勘のスルドい方はお気づきのことでしょう。$z=e^{\frac{2\pi}1i}=+1$ や $z=e^{\frac{2\pi}2i}=-1$ のときって、$\overrightarrow 1$ と $\overrightarrow z$ は線形従属な関係となってしまうため、二次元の基底を成すことはできないはずなのです。
そこで、線形従属を極限とする「ギリギリ線形独立」を扱うというアプローチをします。ハイ、何言ってるのかよくわかんないですよね(汗 大丈夫、すぐに分かると思います(多分)。
まず、$z=e^{i\theta}$ とおき、$e^{xz}=\cos_zx+z\sin_zx$ の両辺をそれぞれ直交座標形式に変換してみましょう。
[左辺]
$$\begin{align}
e^{xz}=&e^{xe^{i\theta}}\\
=&e^{x(\cos\theta+i\sin\theta)}\\
=&e^{x\cos\theta}\cdot e^{ix\sin\theta}\\
=&e^{x\cos\theta}[\cos(x\sin\theta)+i\sin(x\sin\theta)]\\
=&e^{x\cos\theta}\cos(x\sin\theta)+ie^{x\cos\theta}\sin(x\sin\theta)
\end{align}$$
[右辺]
$$\begin{align}
&\cos_zx+z\sin_zx\\
=&\cos_zx+(\cos\theta+i\sin\theta)\sin_zx\\
=&\left[\cos_zx+\cos\theta\sin_zx\right]+i\sin\theta\sin_zx
\end{align}$$
両辺の実部と虚部をそれぞれ比較すると、
$$\begin{cases}
e^{x\cos\theta}\cos(x\sin\theta)=\cos_zx+\cos\theta\sin_zx\\[4pt]
e^{x\cos\theta}\sin(x\sin\theta)=\sin\theta\sin_zx
\end{cases}$$
ですので
$$\begin{cases}
\sin_zx&\displaystyle=\frac{e^{x\cos\theta}\sin(x\sin\theta)}{\sin\theta}\\[4pt]
\cos_zx&\displaystyle=e^{x\cos\theta}\cos(x\sin\theta)-\cos\theta\sin_zx\\
&\displaystyle=e^{x\cos\theta}\cos(x\sin\theta)-\frac{e^{x\cos\theta}\sin(x\sin\theta)}{\tan\theta}
\end{cases}$$
を得られるわけですけども、$\theta$ が $\pi$ の整数倍の場合に分母が $0$ になってしまうのはマズイですよね。この原因は $\theta=n\pi$ のとき $\overrightarrow 1$ と $\overrightarrow{e^{i\theta}}$ が線形従属となってしまうことにあります。そこで、$\theta$ を $t$ とおいて $t\to\theta$ の極限について考えてみようというのが「ギリギリ線形独立」という発想なのです。
$$\begin{cases}
\cos_zx=\displaystyle\lim_{t\to\theta}\left[e^{x\cos t}\cos(x\sin t)-\frac{e^{x\cos t}\sin(x\sin t)}{\tan t}\right]\\
\sin_zx=\displaystyle\lim_{t\to\theta}\left[\frac{e^{x\cos t}\sin(x\sin t)}{\sin t}\right]
\end{cases}$$
$z=e^{\frac{2\pi}1i}=1$ すなわち $\theta=0$ のときを計算すると
$$\begin{cases}
\cos_{+1}x=(1-x)e^x\\[4pt]
\sin_{+1}x=xe^x
\end{cases}\rightarrow~e^{1x}=\cos_zx+1\sin_zx=(1-x)e^x+xe^x
$$
$z=e^{\frac{2\pi}2i}=-1$ すなわち $\theta=\pi$ のときを計算すると
$$\begin{cases}
\cos_{-1}x=(1+x)e^{-x}\\[4pt]
\sin_{-1}x=xe^{-x}
\end{cases}\rightarrow~e^{-1x}=\cos_zx-1\sin_zx=(1+x)e^{-x}-xe^{-x}
$$
というように求まりました。(ウルフラマン先生(Wolfram Alpha)に投げました汗)
さらに、これらの関数をマクローリン展開すると
$$\begin{cases}
\cos_{+1}x=(1-x)e^x&\displaystyle=\sum_{k=0}^\infty\frac{(1-k)x^k}{k!}&\rightarrow~[1,0,-1,-2,-3,-4,\cdots]\\[4pt]
\sin_{+1}x=xe^x&\displaystyle=\sum_{k=0}^\infty\frac{kx^k}{k!}&\rightarrow~[0,1,2,3,4,5\cdots]
\end{cases}$$
$$\begin{cases}
\cos_{-1}x=(1+x)e^{-x}&\displaystyle=\sum_{k=0}^\infty\frac{(1-k)(-1)^kx^k}{k!}&\rightarrow~[1,0,-1,2,-3,4,\cdots]\\[4pt]
\sin_{-1}x=xe^{-x}&\displaystyle=\sum_{k=0}^\infty\frac{-k(-1)^kx^k}{k!}&\rightarrow~[0,1,-2,3,-4,5,\cdots]
\end{cases}$$
となります。ナントこの簡略表記の数列、ガラパゴ累乗定理から求めても見事に一致するんです。プチ感動を味わえるかと思いますので、ぜひご確認くださいませ(*´∀`)
$z\cdotp\overline z=|z|^2=1$ なので $z^n=\underbrace{-(S_{n-1})}_{\cos_zx~側}+\underbrace{(S_n)}_{\sin_zx~側}z$
$$z=e^{\frac{2\pi}1i}=+1~\rightarrow~z+\overline z=2\mathrm{Re}~z=2\\
\begin{cases}
S_0=0\\
S_1=1\\
S_n=-(S_{n-2})+2(S_{n-1})
\end{cases}~\rightarrow~0,1,2,3,4,5,\cdots$$
$$z=e^{\frac{2\pi}2i}=-1~\rightarrow~z+\overline z=2\mathrm{Re}~z=-2\\ \begin{cases} S_0=0\\ S_1=1\\ S_n=-(S_{n-2})-2(S_{n-1}) \end{cases}~\rightarrow~0,1,-2,3,-4,5,\cdots$$
オマケ
最後に、これらを研究していたときに制作した資料がでてきましたので、特別に公開しておきますね。
解説のご要望がございましたら、Discord の DM にて個別に対応いたしますよん。
