楽しそうにやる位相空間 近傍と開基と可算公理
どうも
こんにちは ごててんです 最近概念になりました
位相空間論の勉強に記事を書くことにしました Wikipedia, Mathpedia, 内田集合位相に頼りきった記事です!!! またこの記事は過去の自分に向けて書いています((
この記事の目標は「近傍, 開基, 第1可算公理, 第2可算公理を定義して簡単な性質を示す」ことです
具体的な前提知識 → 可算集合の定義, 距離化可能の定義, 位相空間の定義, 基礎的な解析の知識
(距離空間・距離化可能・位相空間の定義は↓の記事で)
距離化不可能な位相で入門(?)する距離空間
モチベ
位相空間は開集合で記述される幾何学チックな集合だと私は認識しているのですが 今回は可算無限という無限と呼ばれるものの中で最も人間が理解しやすいものの力を使って空間を分類します この可算無限で開集合の「量」を制限します
この記事でやりたいこと
第1可算公理, 第2可算公理, 可分空間を定義したのちに 以下の錬金レシピを示すことです
- 第2可算公理 ⇒ 第1可算公理 + 可分
- 距離化可能 + 可分 ⇒ 第2可算公理
近傍を定義するぞ
第1可算公理を定義する準備として近傍と基本近傍系を定義します
$(X,\mathcal{O})$を位相空間, $x$を$X$の点とするとき, 部分集合$N \subset X$が点$x$の近傍であるとは, 開集合$O \in \mathcal{O}$ があり $x \in O \subset N$ となることである.
$N$は開集合であると限りませんが, $O$は開集合です.
ふわふわ~っと日本語にしましょう 点$x$をくるんと囲む曲線で$N$の中に描けるものが存在するという感じです
ユークリッド平面の点$(1,1)$の近傍を考えます $(0,0)$,$(3,0)$,$(0,3)$を頂点とする三角形(境界を含む)は通常の距離位相で近傍となります $(1,1)$を中心とする半径$\frac{1}{2}$の円(境界を含まない)をとれば, これは開集合であり三角形に含まれるからです(下図).
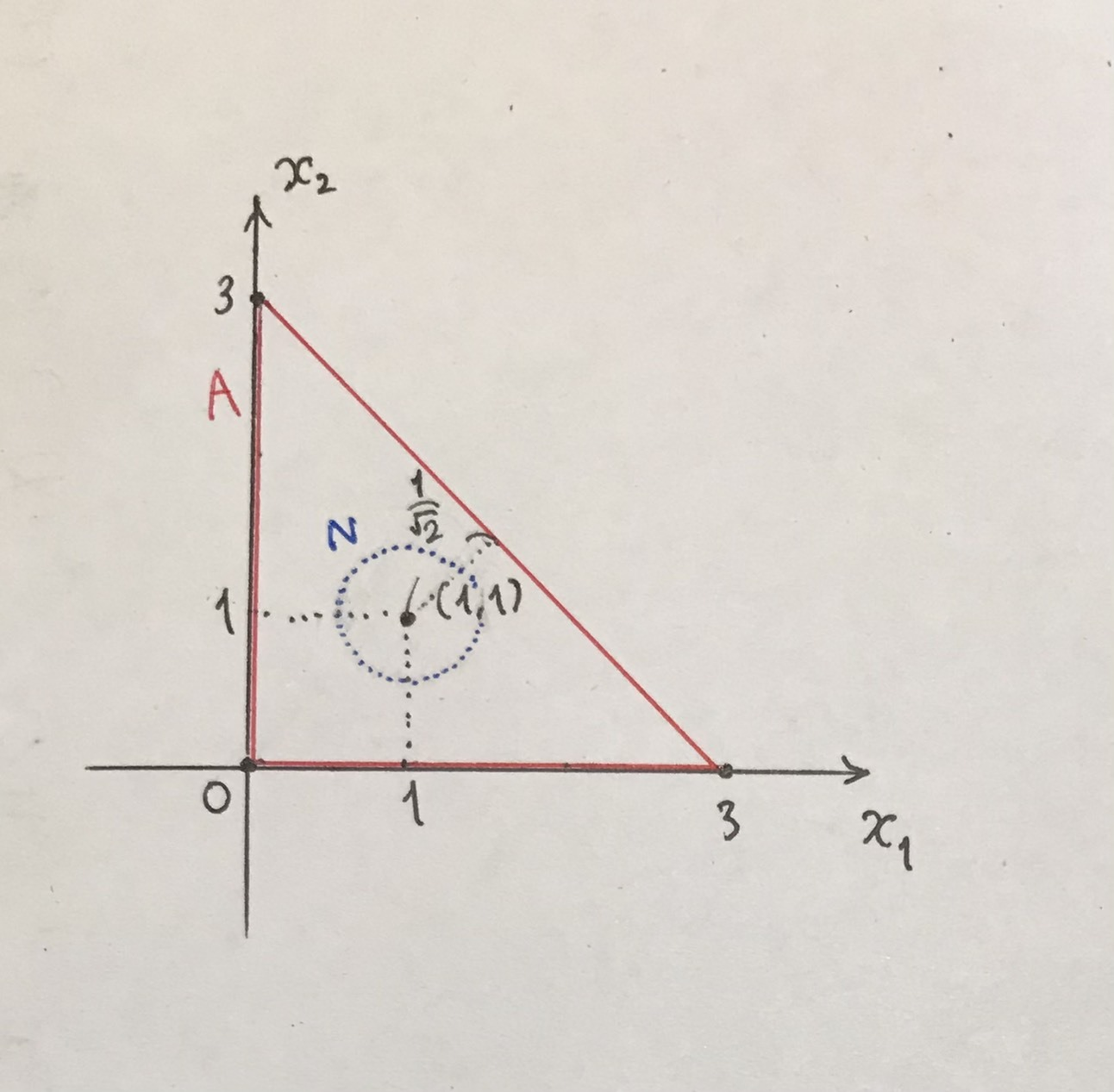 こういう図を書いたの久しぶり
こういう図を書いたの久しぶり
休憩(?)に簡単な命題を示しておきます
$(X,\mathcal{O})$を位相空間, $x$を$X$の点とするとき,$x$を含むような開集合$N \in \mathcal{O}$は$x$の近傍となる.
$x \in N \subset N$ が成立.
さて 近傍でない例も見ておきましょう
ユークリッド平面の点$(1,1)$の近傍を考えます $(0,0)$,$(1,0)$,$(1,1)$,$(0,1)$を頂点とする正方形(境界を含む)は通常の距離位相で近傍となりません!(要証明)(面倒なので証明略)
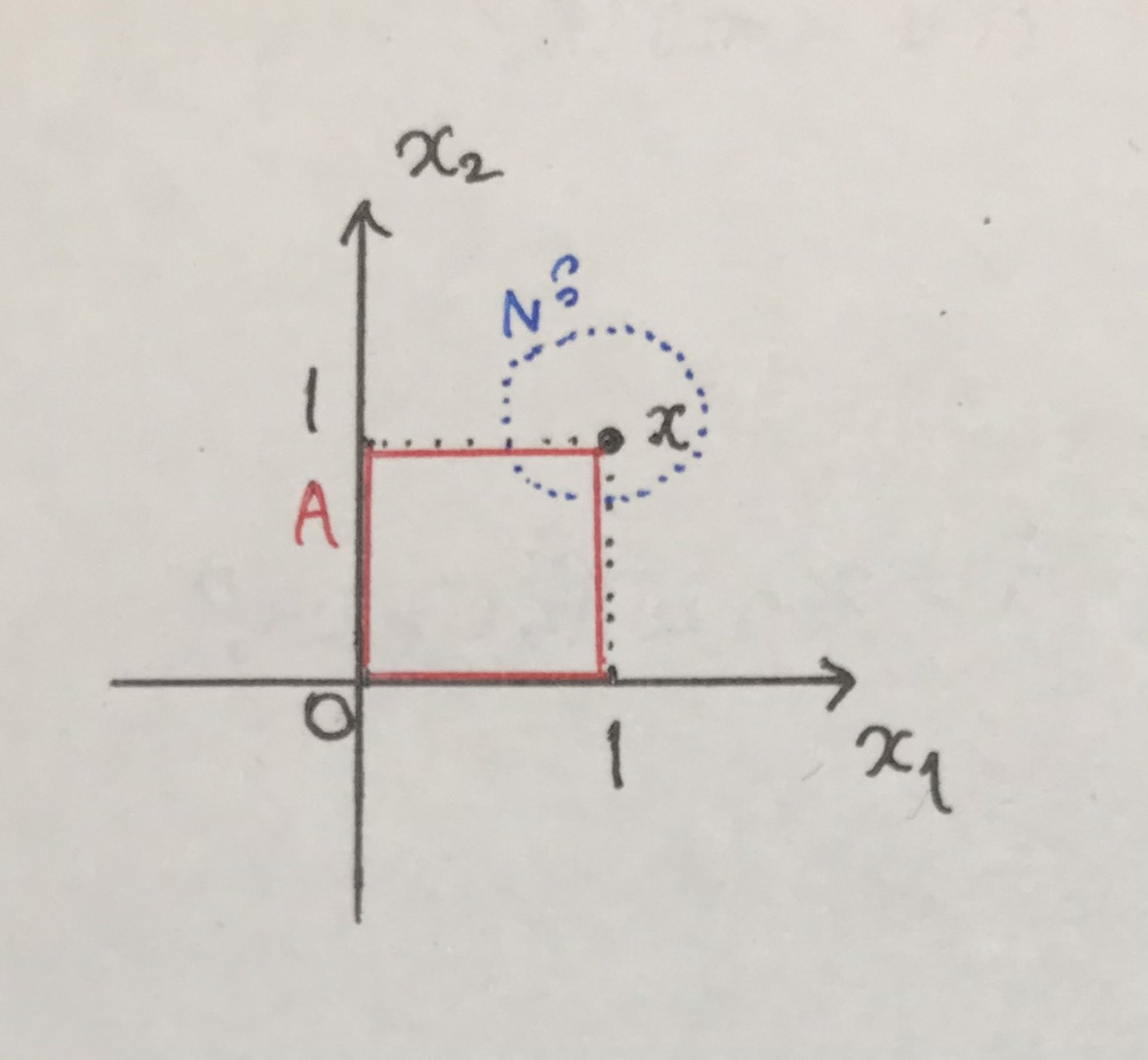 定規って便利
定規って便利
はい! ここで 直感的でないもの代表こと 離散位相さんにお越しいただきました さて離散位相ではすべての部分集合が開集合となるのでした したがって次の命題を得ます
$X$を空でない集合, $x\in X$, $A \subset X$ とするとき, 次は同値.
- $x \in A$.
- $A$は離散位相$(X,2^X)$において$x$の近傍となる.
(1)を仮定すると, $A$は$x$を含み離散位相$(X,2^X)$において開集合であるから命題1を用いればよい. (2)を仮定すると開集合$N \in 2^X$があり $x \in N \subset A$であるから, とくに$x\in A$を得る.
するとどうでしょう 例2は通常の位相で考えれば近傍となりませんが 離散位相で考えれば近傍となることがわかりました! さすが離散位相ですね
さて近傍のイメージがつかめてきたと思います 次に基本近傍系を定義します よくわからないヤツです
$(X,\mathcal{O})$を位相空間,$\mathcal{B}$を$X$の点$x$の近傍からなる集合とする. このとき$x$の任意の近傍$N$に対して$N' \in \mathcal{B}$があり,$N' \subset N$とできれば $\mathcal{B}$は点$x$の基本近傍系であるという.
ふわふわ~~っと日本語にすると どんな近傍をとってきてもそれより小さい近傍を必ずとってこれる便利セットが基本近傍系です なんだかイプシロンデルタを感じますね さて 次の命題を示しておきます これはガッツリ伏線です
$(X,\mathcal{O}_d)$を距離$d$が定める距離位相, また$x\in X$とするとき, 開集合の族$\{ B_{n}(x) \}^{\infty}_{n=1}$ を次で定めると, これは点$x$の基本近傍系となる.
$$ B_{n}(x) = \{ \hspace{2pt} y\in X \hspace{2pt} | \hspace{2pt} d(x,y) < \frac{1}{n} \hspace{2pt} \} .$$
証明の指針を書きます 書いてある証明を読むより指針を読んでそこから証明を完成させるほうが楽しいと思いますし(え)
 全部画像にしたほうがわかりやすい気がしてきた
全部画像にしたほうがわかりやすい気がしてきた
$N$を点$x$の近傍とする. $N=X$であるとき小さい開近傍を取れることは明らかであるので$N \ne X$としてよい.
$I =\inf\{ \hspace{2pt} d(x,y) \hspace{2pt} | \hspace{2pt} y \in X $かつ$ y \notin N \hspace{2pt} \}>0$となることを示す. $I=0$であるとすると, $X$の元で$N$に含まれないような点の列$\{ y_n \}_{n=1}^{\infty} $で$d(x,y_n)<\frac{1}{n}$ となるような列がとれる. $N$は$x$の近傍であることから, 開集合$O$があり $x \in O \subset N$ とできる. さて, $O$は開集合であるから属する点$x$の$\epsilon$近傍$N_{\epsilon}(x)=\{ \hspace{2pt} y\in X \hspace{2pt} | \hspace{2pt} d(x,y) < \epsilon \hspace{2pt} \}$ $ (\epsilon > 0) $がとれて$N_{\epsilon}(x) \subset O$とできる. このとき, $n_0 > \frac{1}{\epsilon}$となる自然数$n_0$をとると$d(x,y_{n_0})<\frac{1}{n_0}<\epsilon$であり, $y_{n_0} \notin N$, とくに$y_{n_0} \notin O$ であることに反する. よって, $I>0$.
$I$の定義より$y\notin N$とすると$d(x,y) \geq I$. 対偶をとると$d(x,y)< I$ ならば$y\in N$,とできる. このとき$n > \frac{1}{I}$とすれば $y \in B_n(x)$ としたとき $d(x,y)<\frac{1}{n}< I$であるから$y\in N$を得る. したがって, $B_n(x) \subset N$.
第1可算公理を定義するぞ
ようやく準備が終わりました 第1可算公理を定義します! ここから読むしんどさが5倍以上になります!!!!
位相空間が任意の点において高々可算個の近傍からなる基本近傍系をもつとき, 第1可算公理を満たしているという.
よくわかりませんね!
わかりやすい性質として 第1可算公理を満たす位相空間において「点列連続ならば連続」が成立します これは実数列での「$x$に収束する任意の数列$\{x_n\}^{\infty}_{n=1}$において$f(x_n) \rightarrow f(x)$ $(n \rightarrow \infty)$ となるなら, $f$は$x$において連続である」という性質に対応します
第1可算公理は近傍に対して可算個の近傍族を用意することで自然数によって添字付けられた点列を支配下にできます 可算という性質は数列のようなものと相性が良さそう!と考えると自然な定義に見えてきますね!見えてくるので 見えてきます 見えてきますよ
逆を言えば点列を扱うなら第1可算公理がないとどうしようもないのかもしれないです(急に自信なさげ)
命題3の系として次を得ます.
距離化可能な位相空間は第1可算公理を満たしている.
よって人間がパッと思いつくような空間では第1可算公理の恩恵を受けることができます
逆は成り立ちません それを紹介します
密着位相$(X,\{\emptyset,X\})$は距離化不可能ですが 第1可算公理を満たします
$x \in X$とするとき, $x$の近傍は$X$のみである. したがって, 任意の点において基本近傍系を$\{X\}$とすればよい.
開基を定義する
第2可算公理を定義するために(深入りしませんが)開基を定義します
開基は位相空間の前段階であり 開集合になれる才能を持った者たちのことです 考える理由の一つとして連続写像であることを示すのがラクになる(開基に属する集合すべてにおいて連続写像っぽい性質が成り立てばその開基によってできる位相空間で連続写像になっている)などのものがあります
さて 定義するだけしてしまいます
$(X,\mathcal{O})$を位相空間とするとき, 部分集合$\mathcal{B} \subset \mathcal{O}$が開基であるとは任意の$X$の開集合が$\mathcal{B}$の元の和集合でかけることである.(空集合も開基から0個の元をとったときの和集合として考える)
よくわからないので具体例を見ていきます
実数全体に通常の位相を入れたとき 開区間の全体は開基になります
例えば $$ \mathbb{R} = \bigcup_{i = -\infty}^\infty (i-1,i+1) $$
のように実数全体は開区間の和集合で表せます
位相空間であることの定義に 無限個の開集合の和集合も開集合である, というものがありました これに対応したものが開基であり この条件を無理矢理満たしてやろう!というのが開基の魂胆です
定義より 開基が存在すればその和集合をとりまくることで位相空間を復元できます!
さて 第2可算公理をば
次に第2可算公理を定義します!!!!!! ...疲れてきたので落ち着きます ハァーッ
位相空間が高々可算個の開集合からなる開基をもつとき, 第2可算公理を満たしているという.
よくわかりませんね 具体例を見ていきましょう
当然ですが $(X,\mathcal{O})$を位相空間とするとき $\mathcal{O}$の濃度が高々可算であれば第2可算公理を満たします($\mathcal{O}$は$\mathcal{O}$の開基となるので) とくに密着位相は第2可算公理を満たします
ユークリッド空間$\mathbb{R}^n$を通常の距離によって距離位相とするとこれは第2可算公理を満たします まじかよ。 証明します
ユークリッド空間$\mathbb{R}^n$を通常の距離によって距離位相とすると, これは第2可算公理を満たす.
証明中に出てくるものを図にしました↓
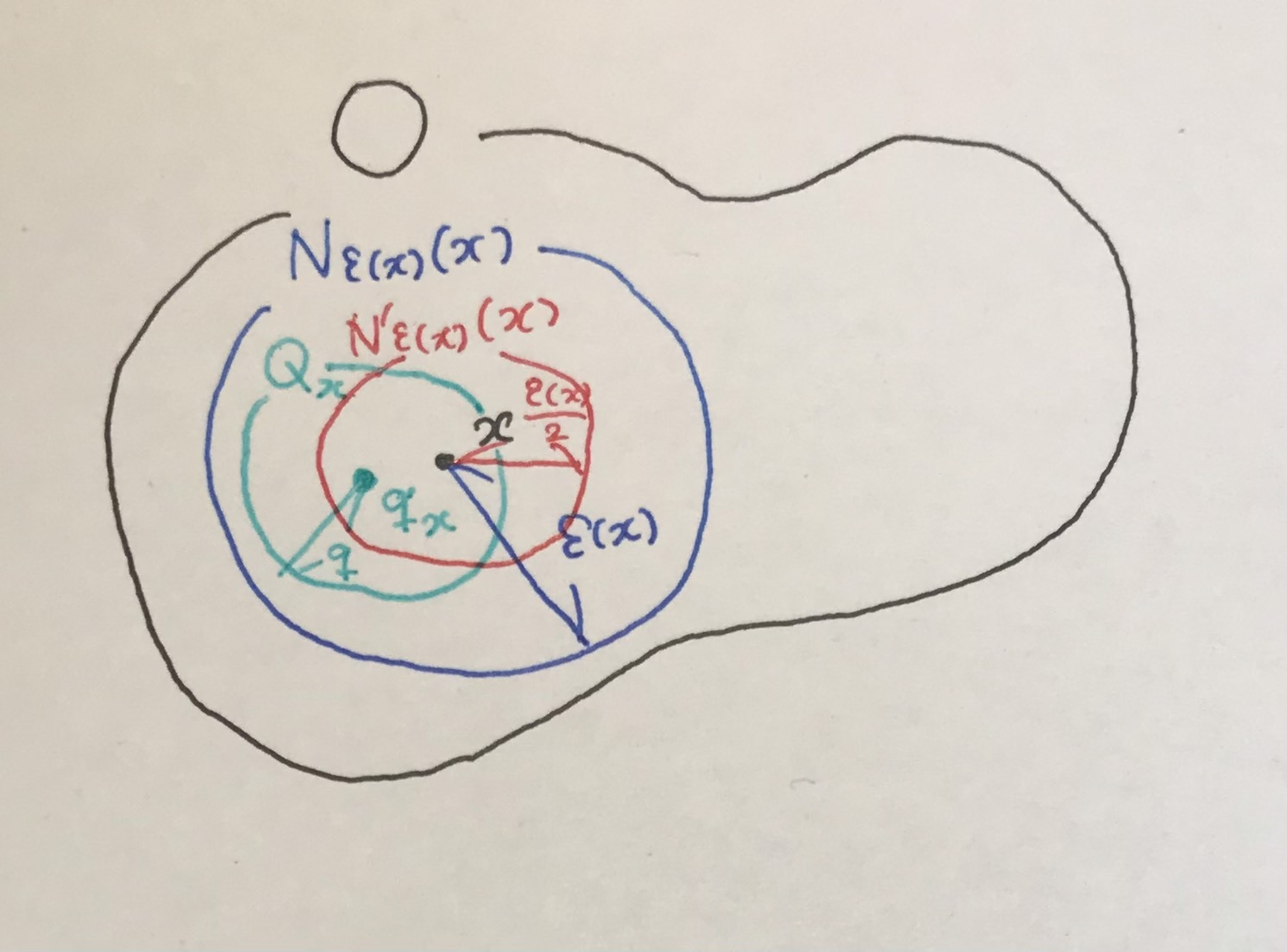 頭が爆発する
頭が爆発する
有理点$\mathbb{Q}^n$を中心とする半径が有理数の$\epsilon$-近傍全体の集合$Q$を考える. この集合の濃度は$|\mathbb{Q}^{n+1}|=|\mathbb{N}^{n+1}|=|\mathbb{N}|$であるので可算集合.
開基となることを示す. $O$を開集合とするとき, $O$の任意の元$x$に対して正の数$\epsilon(x)>0$があり(見やすさの都合から添え字でなく関数の形で書いている)開近傍$N_{\epsilon(x)}(x)=\{ \hspace{2pt} y\in X \hspace{2pt} | \hspace{2pt} d(x,y) < \epsilon (x) \hspace{2pt} \}$を$O$に含まれるようにとれる. 有理数の稠密性より開近傍$N'_{\epsilon(x)}(x)=\{ \hspace{2pt} y\in X \hspace{2pt} | \hspace{2pt} d(x,y) < \frac{\epsilon (x)}{2} \hspace{2pt} \}$の中に有理点$q_x$が取れる. さらに, 有理数の稠密性より$d(q_x,x)< q<\frac{\epsilon (x)}{2}$となる有理数$q$が存在し, $q_x$中心とする半径$q$の開近傍をとるとこれは$N_{\epsilon(x)}(x)$に含まれ, $x$を含み, とくに$O$に含まれる. この有理点$q_x$を中心とする半径が$q$の開近傍を$Q_x$と書く. またこれは$Q$の元である. このとき, $O=\displaystyle \bigcup_{x \in O}Q_x $であるので, 開集合を$Q$の元の和集合で書くことができた.
信じられないぐらい状況把握が面倒な証明になってしまいました
さて 第2可算公理のうれしさを書きます
まず第2可算公理を満たす正規ハウスドルフ空間は距離化可能であるという事実があります(ウリゾーンの距離化定理) あまりに衝撃的です
後は命題の形で書いていきたいと思います(証明が少し重くて今後一切出ないので読み飛ばしてもいいです)
離散位相$(X,2^X)$が第2可算公理を満たすことと, $X$の濃度が高々可算であることは同値である.
離散位相$(X,2^X)$が第2可算公理を満たすとすると, 高々可算個の開集合からなる開基をもつ. $x\in X$とすれば, $\{x\}$は開集合であることから開基の元を可算個とってきて和集合でかけるはずであり, 空でない開基の元$O_1 , \cdots , O_n $をとり $\{x\}=O_1 \cup \cdots \cup O_n$とできる. すると$O_1 \subset O_1 \cup \cdots \cup O_n = \{x\}$ より$O_1 = \{x\}$. よって, 開基は一元集合をすべて含む. (さらに, $X$の部分集合はすべて一元集合の和で表せることから一元集合の全体が開基となることがわかる.) したがって, 開基の濃度が高々可算であることから$X$の濃度も高々可算である. $X$の濃度が高々可算であるとすると, 開基として一元集合の全体をとることができる. これは高々可算の濃度をもつ.
$(X,\mathcal{O})$を第2可算公理を満たす位相空間とすると, $\mathcal{O}$の濃度は高々連続体濃度である.
$(X,\mathcal{O})$を位相空間とするとき, その開基$B \subset \mathcal{O}$をとると, $B$の濃度が高々可算であることから$B$の元の和集合によって表される元のパターンの濃度は$|2^B| \leq |2^{\mathbb{N}}|=|\mathbb{R}|$. したがって, $|\mathcal{O}| \leq |2^B| \leq |\mathbb{R}|$よりわかる.
$(X,\mathcal{O})$を第2可算公理を満たす位相空間とするとき, $V \subset X$に対して開集合族$\{O_{\lambda}\}_{\lambda \in \Lambda}$があり $\displaystyle V \subset \bigcup_{ \lambda \in \varLambda } O_{ \lambda } $となるなら, その開集合族から高々可算個の開集合を選んだ族$\{O_{\lambda_n}\}_{n=1}^{\infty} \subset \{O_{\lambda}\}_{\lambda \in \Lambda}$がとれて, $\displaystyle V \subset \bigcup_{n=1}^{\infty} O_{\lambda_n} $とできる.
$V \subset X$に対して開集合族$\{O_{\lambda}\}_{\lambda \in \Lambda}$を $\displaystyle V \subset \bigcup_{ \lambda \in \Lambda } O_{ \lambda } $となるようにとる. すると$O_{\lambda}$に対して, 開基の部分集合$B_{\lambda}$をとれて, $B_{\lambda}$の元全体の和集合が$O_{\lambda}$となるようにできる. このとき, 開基の部分集合 $\displaystyle B_{\Lambda} = \bigcup_{\lambda \in \Lambda} B_{\lambda} $を考えることができ, 開基が高々可算個の開集合からなることより, $B_{\Lambda} = \{ O'_1 , O'_2 , \cdots \}$とできる(自然数で添字付けることができる). さて, $\displaystyle \bigcup_{\lambda \in \Lambda} B_{\lambda} = \{ O'_1 , O'_2 , \cdots \}$であるから各$O'_n$は$\lambda_n \in \Lambda$があり$O'_n \in B_{\lambda_n}$とでき, $n$に対して$O_{\lambda_n}$を対応させることができる. ここで, $O'_n \subset O_{\lambda_n}$が成立している. $x \in V$とすれば, $\lambda \in \Lambda$があり $x \in O_{\lambda}$. さらに, $B_{\lambda}$の元$O'$があり$x \in O'$が成立. ここで, $O' \in B_{\Lambda}$であるから自然数$N$が存在して $O'=O'_N$. したがって, $\displaystyle x \in O'_N \subset O_{\lambda_N} \subset \bigcup_{n=1}^{\infty} O_{\lambda_n} .$
さて これで第2可算公理のうれしさがいろいろわかりましたね!!! 私はここで証明をいろいろ考えてバテました(疲れた)
閉集合・閉包・稠密
やりたい部分までもう一息です!がんばりましょう!(これは記事を書いている自分に向けて書いています)
可分空間を定義する準備として閉集合・閉包・稠密を定義します
閉集合を深入りせずにスススーっと定義していきます
$(X,\mathcal{O})$を位相空間とするとき, $F \subset X$が閉集合であるとは $X-F \in \mathcal{O}$となることである.
開集合と閉集合は解析学において同時期に定義されるものでおなじみですね そのニュアンスです(投げ) ユークリッド空間における閉集合もその補集合が開集合になっているはずです(投げ)
さて閉包を定義します!!!!!!!
$(X,\mathcal{O})$を位相空間とするとき, 部分集合$A \subset X$に対しその閉包$\overline{A}$を$A$を含む閉集合全体の共通部分と定義する.
閉包を定義しました また一般に閉包は閉集合になります(証明略)(証明しないの!?)
また$A$の閉包は$A$を含む最小の閉集合であり とくに$A=\overline{A}$が成立します
閉集合はこのままだと扱いが難しいので 次の有用な命題を示しておきます
$(X,\mathcal{O})$を位相空間, $A \subset X$を部分集合, $x \in X$とするとき, $x \in \overline{A}$であることと任意の$x$の近傍が$A$と共通部分をもつことは同値である.
$x \notin \overline{A}$とするなら $X-\overline{A}$は開集合であり, これは$A$との共通部分を持たない$x$の開近傍. 対偶を取れば, 任意の$x$の近傍が$A$と共通部分をもてば$x \in \overline{A}$とできる. 逆に, $A$と共通部分をもたない$x\in X$の近傍$N$をとる. すると, $x \in N^i$と$A \subset X - N^i$が成立する. ここで, $X-N^i$は閉集合であるから$\overline{A} \subset X - N^i$であり, $x \notin \overline{A}$. これも対偶をとり命題を得る.
この命題により 元が閉包に含まれることがとても示しやすくなりました!!! これはこの後に定義する可分空間にまつわる命題を示す際の(この記事における)メインウェポンになります この記事を書いているときも技術的なラクさを実感しました(
この記事を読んでいる人が閉集合の定義を知らない確率を考えると稠密性から書いてよかったような気もしますが(?) 準備ができたので稠密性を定義します
$(X,\mathcal{O})$を位相空間とするとき, 部分集合$A \subset X$が稠密な部分集合であるとは, $\overline{A} = X$ となることである.
最も有名な稠密の例を挙げます 有理数全体の集合は実数全体の集合の稠密な部分集合です といいますか この例の一般化が上の定義な気がします
この例からもわかるように $X$のすべての点に対して$A$の元でいくらでも近づくことができる というニュアンスがあります
離散位相では その集合自身のみが稠密な部分集合となります すべての点が離散していますから納得ですね
密着位相では 空でない任意の部分集合が稠密な部分集合となります すべての点が密着していますから納得ですね
可分空間を定義するぞ~~~!
さて この記事の第3の主人公こと 可分空間を定義します
位相空間が稠密で濃度が高々可算な部分集合をもつとき, 可分空間とよぶ
可分空間は「大きすぎない」位相空間になります そう Wikipedia にも Mathpedia にも書いてありました(おい)
可分空間の性質は次の見出しで...(うずうず)
ようやく本題
ここまで長かった... すでに6000文字打っています これは漢検1級の出題範囲となる漢字とほぼ同じ文字数です(謎)
可算公理の関係を調べていきましょう!!! まずはこれ!!!!!!!!!!!!!!!
第2可算公理を満たす位相空間は第1可算公理を満たし, 可分空間である.
$(X,\mathcal{O})$を第2可算公理を満たす位相空間とし, $B$を$\mathcal{O}$の開基で濃度が高々可算であるものとする(これが基本近傍系となることを示す). $x \in X$として, その近傍$N$をとるとき開集合$O\in \mathcal{O}$がとれて $x\in O \subset N$とできる. すると, $O = O_1 \cup O_2 \cup \cdots$ $(O_1 , O_2 , \cdots \in B)$とかけ, 自然数$n$があり $x \in O_n$. したがって, $B$の元の中で点$x$を含むようなものをすべて持ってきた集合は$x$の基本近傍系であり, これは濃度が高々可算な基本近傍系となる. よって第1可算公理を満たす.
$B=\{O'_1 , O'_2 , \cdots \}$のように開基の元を自然数で添字付けておく(また, 空集合は除いておく). このとき点列$\{x_n\}^{\infty}_{n=1}$ を $x_n \in O'_n$となるようにとり, $A=\{ x_n | \hspace{2pt} n \in \mathbb{N} \hspace{2pt} \}$ とする(これが$\overline{A}=X$となることを示す). $x \in X$として, その近傍$N$をとるとき開集合$O\in \mathcal{O}$がとれて $x\in O \subset N$とできる. すると$O$は$B$の元による和集合であるから, 自然数$m$があり$x \in O'_m \subset N$とできる. このとき, $x_m \in N$であるから, $x$の任意の近傍は$A$と共通部分をもち, $x \in \overline{A}$がわかった.
$$ \tiny{自力で証明できなかったのでネットの解答集をみました()} $$
第1可算公理より真に強いことから第2可算公理のネーミングにも納得ですね
では次!!!!!
距離化可能な可分空間は第2可算公理を満たす.
$(X,\mathcal{O}_d)$を距離関数$d$で距離化できる可分空間とする. $\overline{A}=X$となる高々可算な濃度をもつ集合$A \subset X$をとり, $A=\{x_1 , x_2 , \cdots \}$ と自然数で添字付けておく. $N_{\epsilon}(x)=\{ \hspace{2pt} y\in X \hspace{2pt} | \hspace{2pt} d(x,y) < \epsilon \hspace{2pt} \}$とかくとき, $\mathcal{B}=\{ \hspace{2pt} N_q(x_m) \hspace{2pt} | \hspace{2pt} q\in\mathbb{Q} , m\in \mathbb{N} \hspace{2pt} \}$は高々可算な濃度をもつ集合である. これが開基となることを示す. $O \in \mathcal{O}_d$とするとき $x\in O$とすれば近傍$N_{\epsilon}(x) \subset O$をとれる. また$a \in \overline{A}$であることから$x$の開近傍$N_{\epsilon/2}(x)$は$A$と共通部分をもち, $m \in \mathbb{N}$があり$x_m \in N_{\epsilon/2}(x)$(公開から長らく$x_m \in A$と書いてましたが正しくはこっちでした)とできる. ここで, $d(x,x_m)< q<\frac{\epsilon}{2}$を満たす有理数$q$をとると$x \in N_q(x_m)$. さらに, $y \in N_q(x_m)$とすれば $d(x,y) \leq d(x,x_m) + d(x_m,y) < \epsilon$ より $y\in N_{\epsilon}(x) \subset O$であり, $N_q(x_m) \subset O$. よって, すべての点$x$に対して$\mathcal{B}$の元が定まり, それによって$x$に対応する元すべての和集合は$O$に含まれ, また含んでいる.
$$ \tiny{自力で証明できなかったのでネットの解答集をみました()} $$
この命題から 距離空間において可分空間であることと第2可算公理を満たすことが同値であるとわかりました!!!
まとめ
この記事をまとめると以下のような感じです
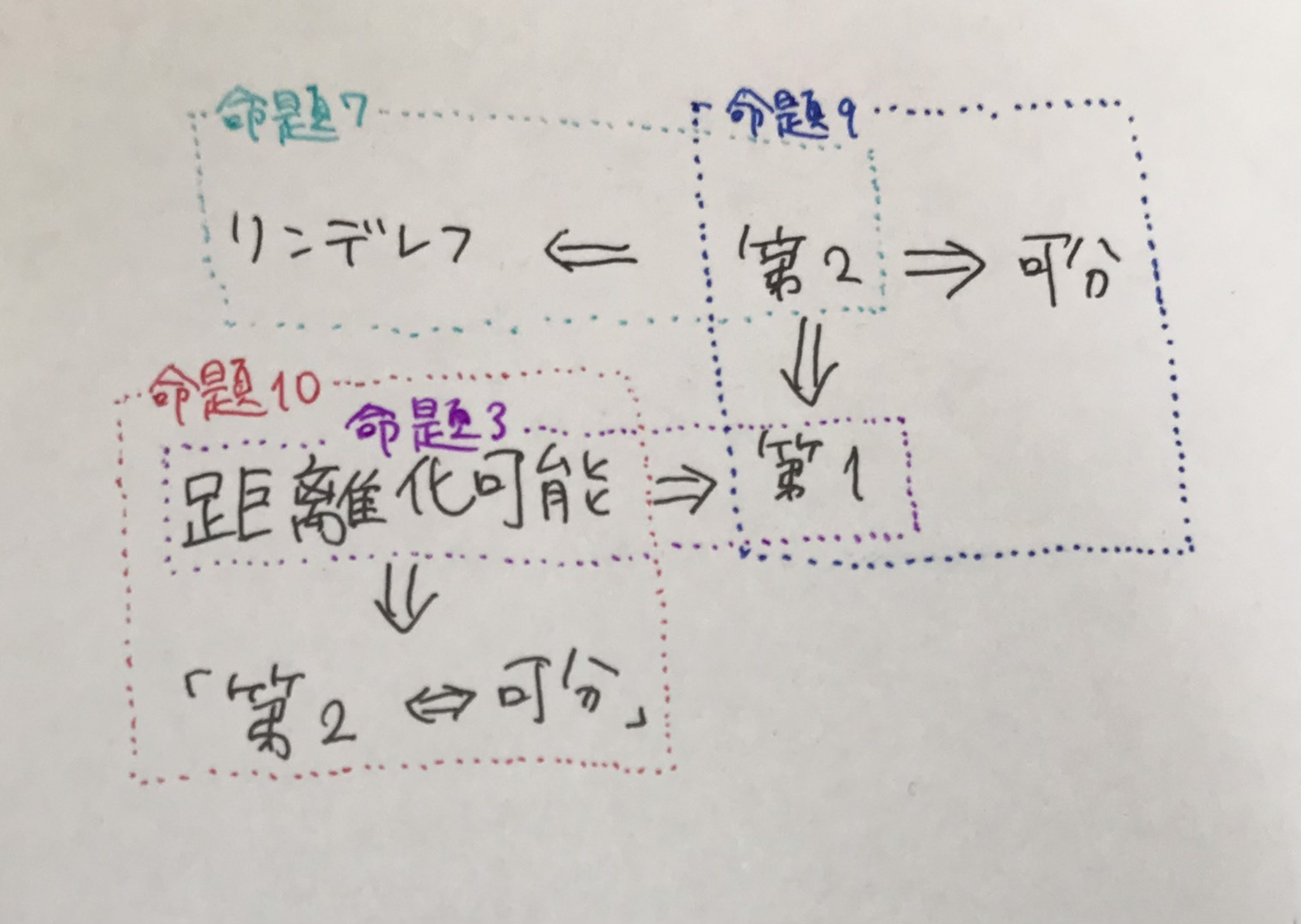 結構示しましたね~~
結構示しましたね~~
気軽に書き始めたのですがかなり長い記事になってしまいました((
ここまで読んでいただきありがとうございました!!!
見やすい / 面白いと思っていただけた方 グッドよろしくおねがいします~~~
それでは!
