文献あり

相対論：解けますか？双子のパラドックスより"易しい"問題

3802

双子のパラドックスより基本的な問題

相対論で有名な「双子のパラドックス」、多くの人は聞いたことがあるかと思います。それはこんなパラドックスです：

AとBは双子である。Aは地球にいる。Bは宇宙船で遠くの星まで行き、その後地球に戻ってくる。相対論では動いている系の時間は遅れるので、AよりBのほうが若くなる。一方、Bから見ればAのほうが動いており、ゆえにBよりAのほうが若くなる。これは矛盾。（図1参照）

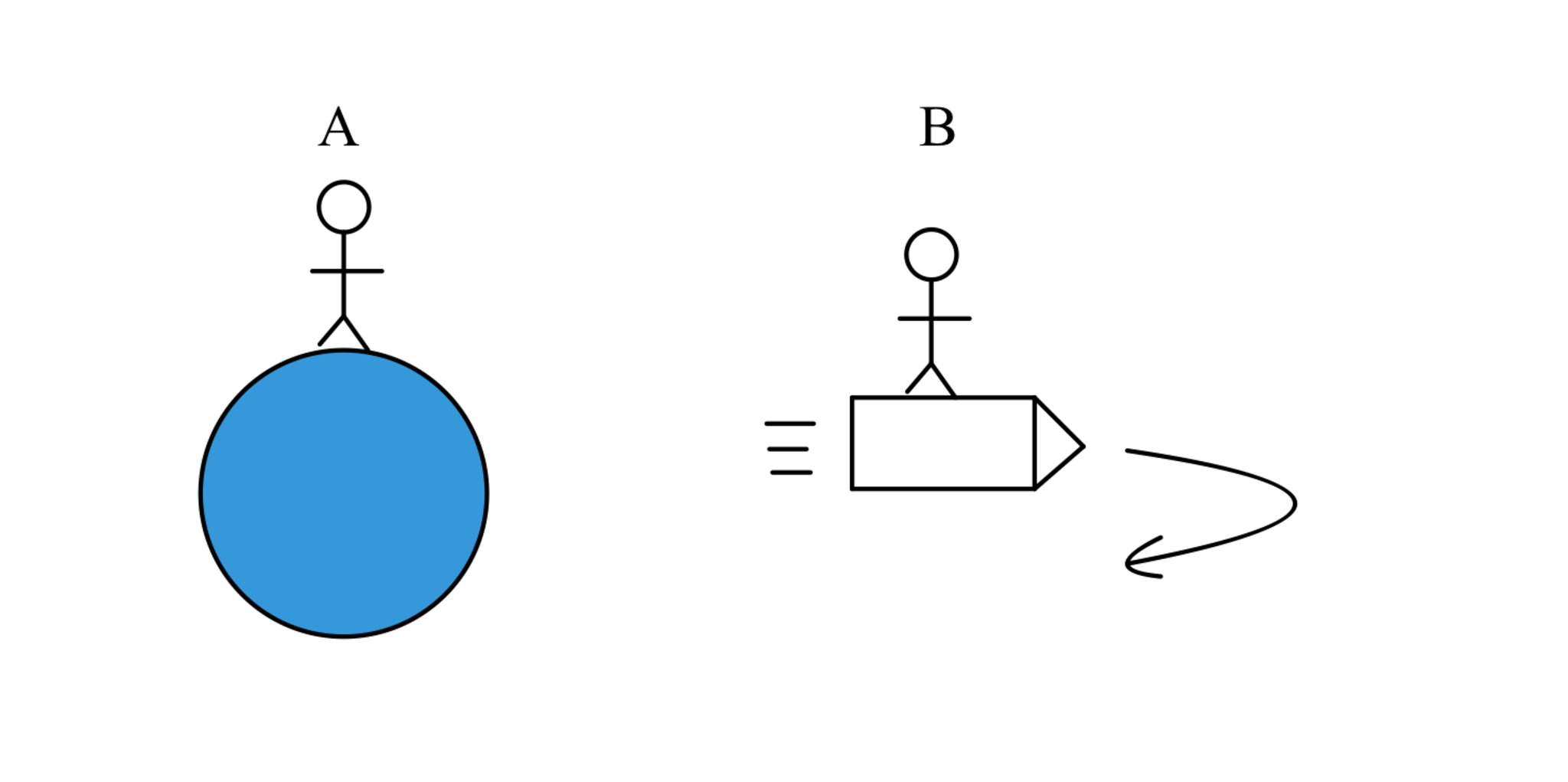双子のパラドックスの設定

この矛盾は、「AとBの運動が相対的でない」ことで解決されます。Aは常に慣性系（等速直線運動をする系。加速度運動をしない系）にいるのに対し、Bは加速度運動をしています。この違いを考慮し計算すると、BのほうがAより若くなります。この話は非常に有名であるがゆえに、解答を知っている人は多いです。

しかし、この高度なパラドックスの前に、もっと簡単な、お互いに等速直線運動をしているときのことを考えてみましょう。例えば、"等速直線運動双子のパラドックス"：「Aは地球にいて、Bは宇宙船に乗っているが、この宇宙船は加速度運動をせず、ずっとまっすぐ飛んでいる」を考えます。このとき運動は完全に相対的です。すると相対論によれば、「お互いに時間が遅れる」はずです。

しかし「お互いに時間が遅れる」ってどういうことでしょう？

この解答は、もちろん有名ではありますが、双子のパラドックスの解答ほどは一般には知られていないのではないでしょうか。これに関して考察してみます。

上の"等速直線運動双子のパラドックス"だと、双子なのにずっとBが宇宙を旅しているのも変だし、どうやって時間を比べるかもわからないので、設定を変えます：

問題

電車が一定の速度で走っている。電車の中にいるBは腕時計をしている。P駅を通りすぎるとき、Bが窓から駅を見ると、Bの腕時計とP駅の時計はどちらも1時を指していた。しばらくののちQ駅を通りすぎるとき、窓からQ駅の時計を見たら2時を指していた。このときBの腕時計は

2時より前を指している
2時より後を指している
2時を指している

のどれか（図2参照）。

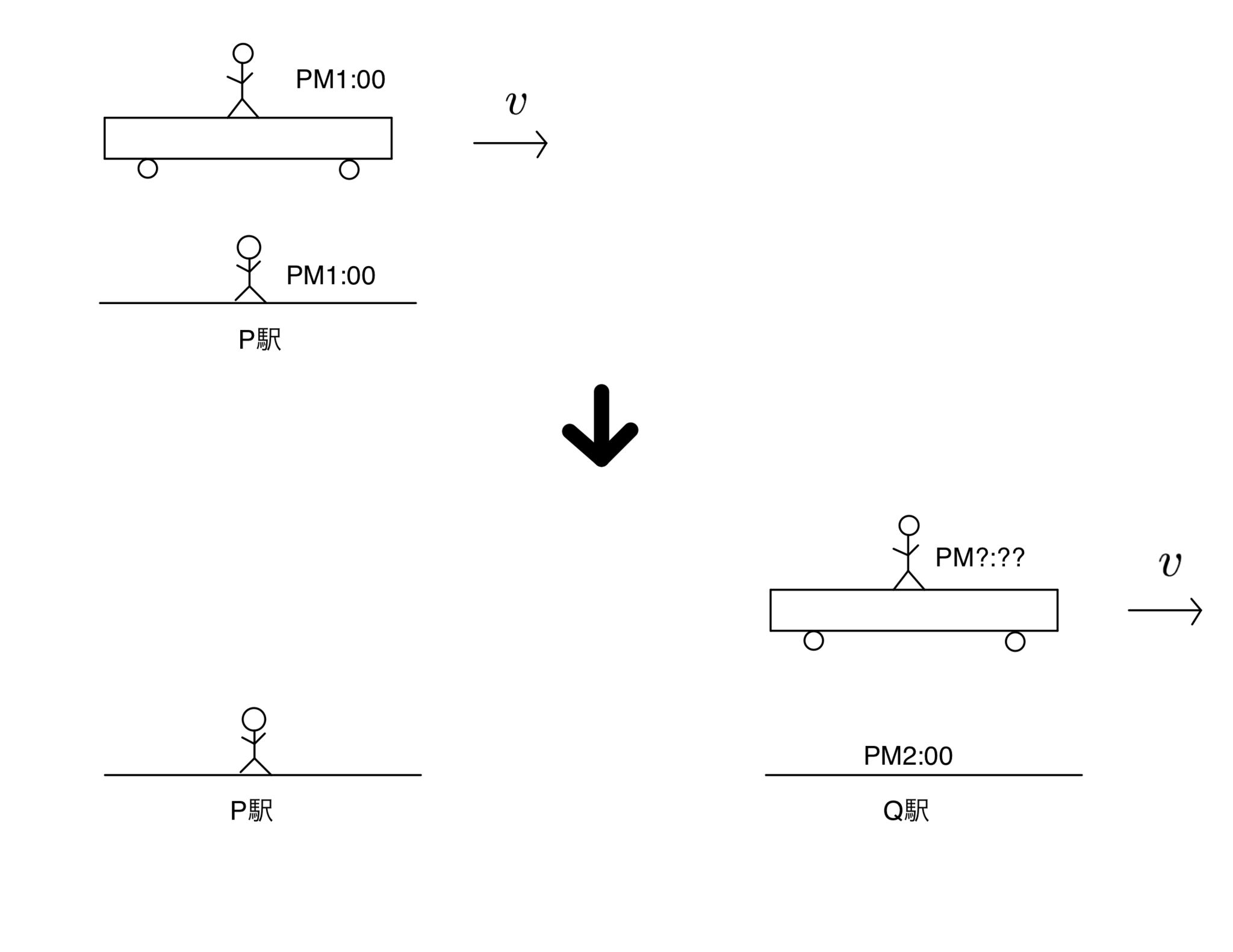問題の設定

P駅に駅員Aがいるとすれば、状況は上記の直線運動双子のパラドックスと同じです。運動は完全に相対的なので、駅員AからみればBの時間は遅れ、Bから見ればAの時間は遅れているはずです。しかし、もし1.が答えなら、Bから見たらAはむしろ時間が進んでいるし、2.が答えならその逆。3.が答えなら、時間の進み方は同じで、遅れなどない。遅れがなければ、相対論は正しくないことになる。1.2.3.どれも違うなんてことはありえない。ということで、これはパラドックスに見えます。

この問題の解答は

1. 2時より前を指している

です。一見相対論に矛盾しているように見えますが、BからみるとP駅とQ駅の時計がずれていることで無矛盾になります。

以下詳しく見ていきます。

定性的な解答

Aから見たBの時間の遅れは簡単です。Q駅での時計の読みとBの腕時計の読みをそのまま比べればいいです。駅の時計は2時。腕時計は"運動している系の時間の遅れ"により2時より前。よってAから見たらBの時間は遅れています。

問題はBから見たAの時間です。
Bから見るとQ駅の時計はP駅とずれていることが問題を解決します。重要なのは、2駅の時計は駅の静止系で同期されていることです。特殊相対論の最も重要な帰結は、「離れた2点の同時刻は慣性系により異なる」ことです。Aにとってはいつでも2駅の2つの時計は同期されていますが、異なる慣性系のBにとっては、Q駅にいるときP駅の時計は同期されていません。そのため、Q駅の時計が2時を指していても、このとき(=Bにとっての同時刻において)P駅の時計は時間の遅れにより2時より前です。最初にP駅の時計で時刻の起点を設定したのだから、Q駅の時計ではなく、P駅の時計で時間の経過を測るべきです。これを考慮し定量的な計算を行えば、Bから見てもAの時間が遅れていることが言えます。

上の「AからみたBの時間の遅れ」において「Q駅での時計の読みとBの腕時計の読みをそのまま比べ」たのは、P駅とQ駅が同じ慣性系にあり、時計合わせがなされているという暗黙の前提によるものです。

定性的にはここまでしか言えません。以下定量的に議論しましょう。

定量的な解答(1) 相対性による"自明な"議論

まずは時間の遅れの相対性を、よくある「A系から見たB系での経過時間はA系の座標で計算し、B系から見たA系の経過時間はB系の座標で計算する」という方法で見てみましょう。相対論が相対性を満たすという当然の事実の確認に相当します。しかし、先に述べておきますが、この計算は上記問題のパラドックスの解決を与えません。次の「定量的な解答(2) 一貫してA系の座標で考える」でその解決を与えます。

今、Bがいる電車の慣性系をB系、Aがいる駅の慣性系をA系と呼ぶことにします。また、B系の座標をプライム付きの記号で、A系の座標をプライムなしの記号で表すことにします。簡単のため時間と空間1次元の場合を考えます。光の速度がA系でもB系でも等しく $c$ とすると、これに相対性原理を課すことで、
$\begin{aligned} t^{'} & = \frac{t - (v / c^{2}) x}{\sqrt{1 - β^{2}}} (1), \\ x^{'} & = \frac{x - v t}{\sqrt{1 - β^{2}}} (2) \end{aligned}$
という関係が成り立ちます（詳しい証明は「相対論: Lorentz変換の導出」を御覧ください）。 $t, x$ はそれぞれA系の時間座標と空間座標、 $t^{'}, x^{'}$ はB系の時間座標と空間座標です。また、 $v$ は電車の速度、 $c$ は光の速度、 $β := v / c$ です。この式は認めてもらうことにします。Aは $t$ の時間、Bは $t^{'}$ の時間のもとに過ごしていることに注意してください。
A系とB系の原点に時計を置きます。A系の原点とB系の原点は、駅Pにおいて一致していることにしましょう。電車がA系に対し速度 $v$ で動くとすると、
$\begin{array}{r} x = v t \end{array}$
がB系の原点 $(x^{'}, t^{'}) = (0, 0)$ をA系からみた座標になります。これを(1)に入れることで、A系の時間とB系の時間の関係がわかります：
$\begin{array}{r} t^{'} = \sqrt{1 - β^{2}} t < t \end{array}$
つまり、A系からみて、B系の時間は遅れています。

逆にB系からみると、A系は逆方向に走っているから、上の式で $t^{'}, x^{'} \leftrightarrow t, x$ かつ $v \to - v$ とした
$\begin{aligned} t & = \frac{t^{'} + (v / c^{2}) x}{\sqrt{1 - β^{2}}} (3), \\ x & = \frac{x^{'} + v t^{'}}{\sqrt{1 - β^{2}}} (4) \end{aligned}$
が成立します。さらに $(x, t) = (0, 0)$ はB系からみると
$\begin{array}{r} x^{'} = - v t^{'} \end{array}$
であるから、上と同じ計算により
$\begin{array}{r} t = \sqrt{1 - β^{2}} t^{'} < t^{'} \end{array}$
となります。
以上から時間の遅れは完全に相対的で「お互いに時間が遅れる」ことがわかります。

しかし、この説明だと本問題の解決がどうなされるかわからないです。この計算はA系の座標でBの時間の遅れを計算したものと、B系の座標でAの時間の遅れ計算したものを比較しています。式(1)(2)(3)(4)は相対性原理を仮定して導かれているので、このような相対性が成り立つのはほぼ自明です。この問題に答えるには、どちらかの立場のみにたって考える必要があります。以下、一貫してA系の座標を使うことで時間の遅れを説明します。

定量的な解答(2) 一貫してA系の座標で考える

以下はシュッツ著「相対性理論（上）」の解説と本質的に同じ議論です。

まず準備をします。
図3を見てください。これは時空図と呼ばれるものです。縦軸がA系の時間座標 $c t$ 、横軸がA系の位置座標 $x$ です。空間軸と同じ次元になるように時間軸には $c$ をかけてあります。Cの $x$ 座標( $x = 0$ )がP駅の場所、Dの $x$ 座標がQ駅の場所です。P駅の時計は $x = 0$ に、Q駅の時計はDの $x$ 座標の場所に固定されています。B系の原点 $(c t^{'}, x^{'}) = (0, 0)_{B}$ （時間を最初に、空間を後に書くことにします）はCからDまで動き、その軌跡が図に描かれています。以下わかりやすいように、座標を表すときには適宜suffixとして $A, B$ をつけ、どちらの座標で場所を表しているかを明確にすることにします。Aの時間は $t$ の時間の下にあるP駅の時計で、Bの時間は $t^{'}$ の時間の下にある腕時計で測っていることに注意してください。
Bの原点は $x = v t$ 上を走っているので、図の $θ$ は
$\begin{array}{r} \tan θ = β \end{array}$
を満たします。もう一つ、世界線の長さという大切な概念があります。どんな慣性系でも
$\begin{array}{r} Δ s^{2} := - (c Δ t)^{2} + Δ x^{2} \end{array}$
の値は変わりません。これはどの系からみても光の速度が変わらないことを式で表したものです。これが特殊相対論での(=Minkowski空間での)2点の長さを決める式です。この $Δ s$ が世界線の長さです。時空図における物体の軌跡の長さは $Δ s$ であり、上記式により計算します。
以下" $i$ 系( $i = A, B$ )において点Rから点Sまでの移動で経過した時間"を ${T m}_{i}^{(R S)}$ と表すことにします。

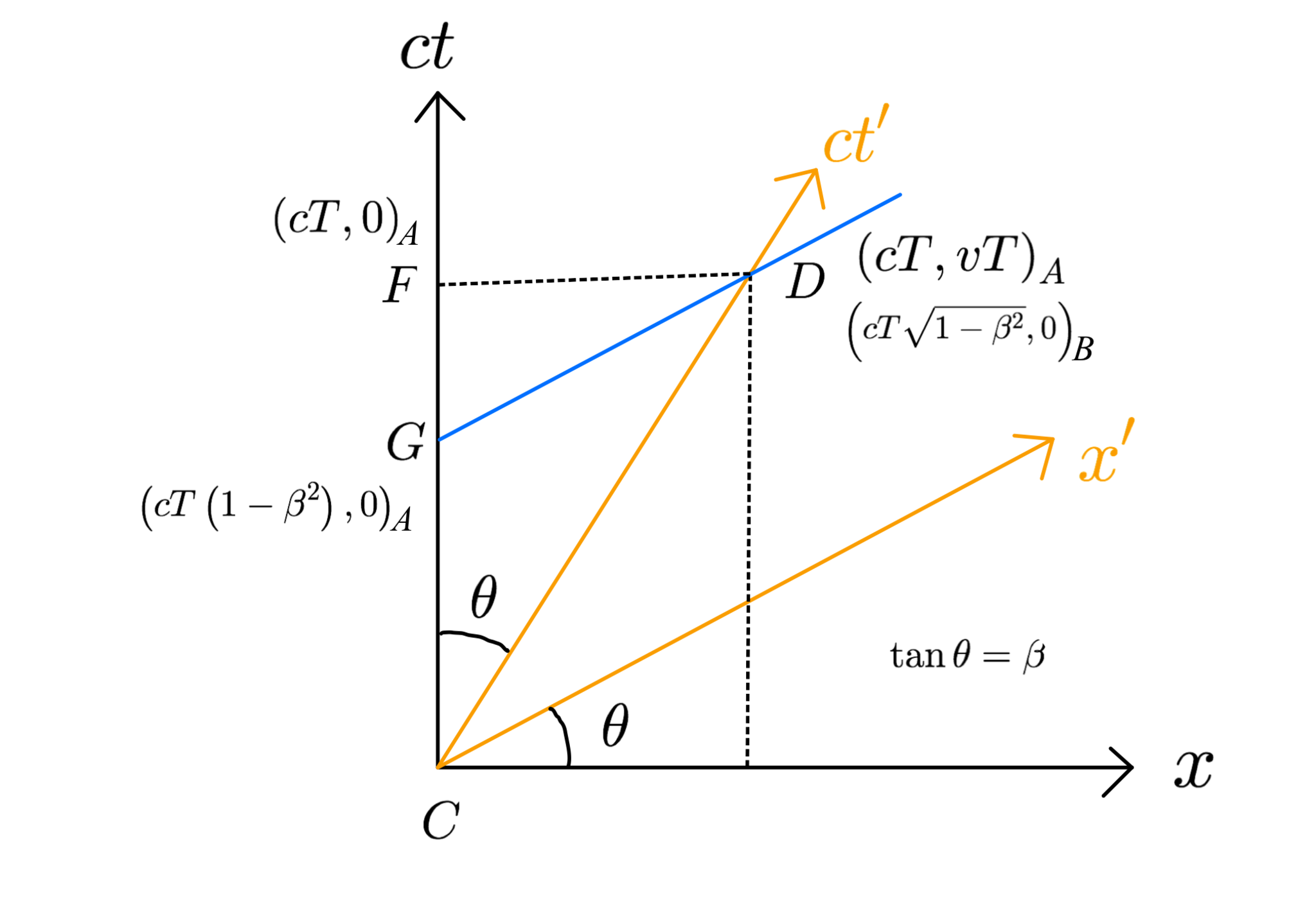問題の状況の時空図。P駅とQ駅はそれぞれCとDのx座標の位置にある。水色の線はx'軸に並行。

以上で準備は終わりです。まず最初に、この議論に必要な、計算すべき量を明確にしておきましょう。それは以下の3つの量です：

計算すべき量

BがCからDまで動く間のP駅の時計の進み: ${T m}_{A}^{(C D)}$
BがCからDまで動く間のBの腕時計の進み: ${T m}_{B}^{(C D)}$
BがCからDまで動いたとき（=BがQ駅についたとき）、同時刻におけるP駅の時計の進み: ${T m}_{A}^{(C G)}$

1.2.が必要な理由はすぐにわかるかと思います。問題は3.です。この量は、Bから見たAの経過時間ですが、1.と等しくはないです。なぜなら、BからみたDと同時刻のP駅の時計はFではなくGに存在するからです。時刻の起点はP駅の時計で測っているため、時刻の終点もP駅の時計で測る必要があり、 ${Tm}_{A}^{(C G)}$ がBから見たAの経過時間になります（後述）。

1.2.3.を計算しましょう。

${T m}_{A}^{(C D)}$
これは $T$ と仮定します。
${T m}_{B}^{(C D)}$
1よりFの座標はF: $(c T, 0)_{A}$ です。このときDの座標をA系の座標で表すと、D: $(c T, v T)_{A}$ であることはすぐにわかります。ではBの腕時計はDでどの値を示すでしょうか。そのためには、B系の座標 $(t^{'}, x^{'})$ でDを表す必要があります。それには次の2つ
・ Dは移動中ずっとB系の時間軸上にあり、 $x^{'} = 0$
・ $\overset{―}{C D}$ の世界線の長さはどの座標でも変わらないので、 $- (c T)^{2} + (v T)^{2} = - (c t^{'})^{2} + x^{' 2}$
を使います。これらより $t^{'} = T \sqrt{1 - β^{2}} (β := v / c)$ になります。よってD: $(c T \sqrt{1 - β^{2}}, 0)_{B}$ です。C: $(0, 0)_{B}$ なので、
$\begin{array}{r} {T m}_{B}^{(C D)} = T \sqrt{1 - β^{2}} \end{array}$
です。BはずっとB系の時間軸上を移動しているので、単に2点の時間差を計算すればよいことに注意してください。A系ではD: $(c T, v T)_{A}$ , C: $(0, 0)_{A}$ であるので
$\begin{array}{r} {T m}_{A}^{(C D)} = {T m}_{A}^{(C F)} = T \end{array}$
です。
${T m}_{A}^{(C G)}$
まず、Bから見ると、Dと同時刻のP駅の点がGであることを説明します。B系の同時刻はB系の時間で時刻一定 $c t^{'} = c α$ ( $α$ は定数)を満たす線です。これがA系の座標でどう表されるかは、 $c t^{'} = c α$ を(1)に入れればわかります。これにより、B系の同時刻を表す直線はA系の座標では
$\begin{array}{r} c α = \frac{c t - β x}{\sqrt{1 - β^{2}}} \end{array}$
となります。これは図の水色の線です。Dの時間座標はB系の座標で表せば $t^{'} = T \sqrt{1 - β^{2}}$ なので $α = T \sqrt{1 - β^{2}}$ を代入、またP駅は $x = 0$ なので、G: $(c T (1 - β^{2}), 0)_{A}$ です。結局B系から見てDと同時刻であるP駅の時計の経過時間、すなわち ${T m}_{A}^{(C G)}$ は
$\begin{array}{r} {T m}_{A}^{(C G)} = T (1 - β^{2}) \end{array}$
となります。

以上から

・BがCDの間に経験した時間 ${T m}_{B}^{(C D)} <$ AがCDの間に経験した時間 ${T m}_{A}^{(C D)} (= {T m}_{A}^{(C F)})$

であり、Aから見るとBの時間が遅れている。

・AがCGの間に経験した時間 ${T m}_{A}^{(C G)} <$ BがCDの間に経験した時間 ${T m}_{B}^{(C D)}$

であり、Bから見るとAの時間が遅れている。

がわかります。

これをまとめると次の表になります：

	自身の経過時間 (1)	相手の経過時間 (2)	(2)/(1)
Aから見る	${T m}_{A}^{(C D)} = {T m}_{A}^{(C F)} = T$	${T m}_{B}^{(C D)} = T \sqrt{1 - β^{2}}$	$\sqrt{1 - β^{2}}$
Bから見る	${T m}_{B}^{(C D)} = T \sqrt{1 - β^{2}}$	${T m}_{A}^{(C G)} = T (\sqrt{1 - β^{2}})^{2}$	$\sqrt{1 - β^{2}}$

このように、どちらからみても相手の時間が遅れ、かつ

相手の経過時間/自身の経過時間 $= \sqrt{1 - β^{2}}$

となっています。

双子のパラドックスの解決

ここまで理解すれば、元の双子のパラドックスはすぐ理解できます。計算も終わったも同然です。

BがQ駅にさしかかったとき、電車が一瞬で止まったら何が起きるでしょう。一瞬で止まろうとも、Bが経験する時間は同じように流れます。よって腕時計の針が突然変化することはありません。そして、同じ場所にあるQ駅の時計が突然変化することもありません。たとえ違う2つの系にいる2人でも、同じQ駅にいるなら、そこで起こることに関し、同じことを目にし経験します。そして電車が止まることで、一瞬にしてP駅Q駅と同じ慣性系に乗り換えます。ということは、止まった直後、Bの腕時計は2時より遅れており、（止まった後の）同時刻ではPの時計は2時です。これで確かに、AのほうがBより年をとったことになります。年齢を会って比較したければ、P駅に戻ればいいです。戻るときにゆっくり戻れば、電車で得た時間差を保つことができます。これで双子のパラドックスとおなじシチュエーションになります。

この双子のパラドックスにおける時間の遅れの計算では、加速度による時間の遅れ等ダイナミカルなことは考慮してません。突然慣性系を乗り換えるだけです。これは突然止まるという場合にしか使えませんが、考え方・計算はシンプルです。

時間の測り方の違い

ここまで見てきたように、A系のみの視点でも時間の遅れの相対性が説明できることがわかりました。しかし上の表を見るとわかるとおり、A系のみの視点で計算すると、完全な相対性は成立していません。例えば「Aから見たBの経過時間」と「Bから見たAの経過時間」は異なっています。一方で、「相対性による"自明な"議論」では、完全に相対性が成り立っています。

この違いは、A系のみの視点で時間の遅れを計算する場合、AとBで相手の経過時間を測るセットアップに非対称性があることに起因します。Aは違う2点にある同じ慣性系で同期された2つの時計を使ってBの時間を測ります。一方で、BがAの経過時間を測るときは、自身の時計および違う慣性系にあるP駅の時計で経過時間を測っています。

Aから見た場合、計算した経過時間は、お互いにとって"実際に経過した時間"です。つまり、Aから見て、BがCからDに移動するのにかかった時間は、Aにとっては $T$ だし、Bにとっては $T \sqrt{1 - β^{2}}$ でした。これはどちらも実際に自身が経験した経過時間です。一方で、Bから見たAの経過時間は $T (1 - β^{2})$ でしたが、これはBがCからDまで移動する間にAが経験した時間ではありません。これは上記のセットアップの違いによるものです。そもそもこの問題自身が非対称なセットアップになっているので、しょうがないです。セットアップを対称にしたければ、Bから見たAの経過時間を計算する場合、電車が非常に長く、その電車の2地点に同期された時計を置くことで、AがBの経過時間を測るときと同じシチュエーションにする必要があります。「定量的な解答(1) 相対性による"自明な"議論」で行った計算は、いわばこの後者のやり方でお互いの時間を対称なセットアップにより計算したようなものです。

これに対し、オリジナルの双子のパラドックスは、宇宙にいたBが最終的に地球に戻ってくるため、どちらも自身の時計のみでその経過時間を測れます。

この2つの問題の違いを標語的に言えば
・双子のパラドックスでは運動の相対性が破れているが、時間の測り方は相対的
・本問では時間の測り方の相対性が破れているが、運動は相対的
という感じです。
「お互いに時間が遅れる」というパラドックスが起きないのは、運動の相対性と時間測定の相対性の両方を満たすことができないから、と言ってもいいかもしれません。

おしまい $_{◼}$

Appendix: 固有時

固有時という概念があります。上のほうで、 $Δ s^{2}$ なる量を定義しました。これとほぼ同じような量ではありますが、 $Δ s^{2}$ の単位が長さであることと、この定義そのままだとtime-likeな2点（因果を持てる2点、光円錐内の2点）に対して $Δ s^{2}$ が負になることから
$\begin{array}{r} c^{2} (Δ τ)^{2} \equiv - Δ s^{2} \end{array}$
なる時間の次元をもつ量を定義します。このとき $Δ τ$ はtime-likeな2点に関して正になります。重要なことは、この量はLorentz不変であること、および自分が止まっているとする立場にたち、 $Δ x = 0$ とした場合、
$\begin{array}{r} Δ τ = Δ t \end{array}$
となり、そのまま自分の経験した時間になることです。

CからDまで移動したときの固有時をA系で計算してみます（どの系で計算しても不変ですが）。C: $(0, 0)_{A}$ , D: $(c T, v T)_{A}$ なので
$\begin{array}{r} Δ s^{2} = - c^{2} T^{2} + v^{2} T^{2} \end{array}$
固有時になおすと
$\begin{array}{r} Δ τ = \sqrt{- Δ s^{2}} / c^{2} = T \sqrt{1 - β^{2}} \end{array}$
となり、先程計算した「BがCからDまで移動するときに経験する経過時間」と一致します。

一般に、時空図の2点を移動するものの経過時間は、その経路がある系で $x = f (t)$ であらわされるとき、世界線のLorentz不変性
$\begin{array}{r} - (c Δ t^{'})^{2} = - (c Δ t)^{2} + Δ f^{2} \end{array}$
より
$\begin{array}{r} Δ t^{'} = Δ t \sqrt{1 - \frac{1}{c^{2}} {(\frac{d f}{d t})}^{2}} \end{array}$
となるので、
$\begin{array}{r} t^{'} = \int_{0}^{t^{'}} d t^{'} = \int_{0}^{t} \sqrt{1 - \frac{1}{c^{2}} {(\frac{d f}{d t})}^{2}} d t \end{array}$
を計算すればよいです。この計算は慣性系でなくても適用できることに注意してください。