Fibonacci 数の行列表示とその応用
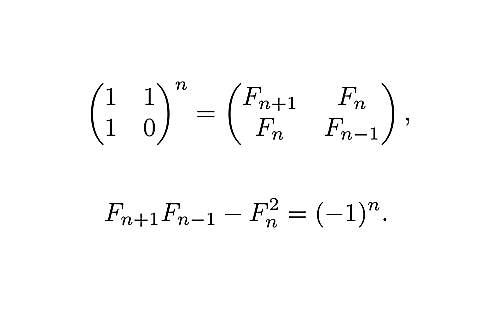 行列表示
行列表示
前提知識 : Fibonacci 数列, 二次正方行列の行列式, 対角行列の累乗, 二元一次不定方程式
Fibonacci 数列 :
https://mathlog.info/articles/191
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
行列表示
任意の$n\in\mathbb{Z}$に対して, $P=\left(\begin{array}{cc}1&1\\ 1&0\end{array}\right)$の表記の下で以下が成りたつ.
$\quad(1)\quad\left(\begin{array}{cc}L_{n+1}&L_n\\ L_n&L_{n-1}\end{array}\right)=P^n\left(\begin{array}{cc}1&2\\ 2&-1\end{array}\right).$
$\quad(2)\quad\left(\begin{array}{cc}F_{n+1}&F_n\\ F_n&F_{n-1}\end{array}\right)=P^n.$
自明な等式
$$
\begin{align}
&\left(\begin{array}{cc}L_{n+1}&L_n\\L\ _n&L\ _{n-1}\end{array}\right)=\left(\begin{array}{cc}1&1\\ 1&0\end{array}\right)\left(\begin{array}{cc}L_{n}&L_{n-1}\\ L_{n-1}&L_{n-2}\end{array}\right),\\
&\left(\begin{array}{cc}F_{n+1}&F_n\\ F_n&F_{n-1}\end{array}\right)=\left(\begin{array}{cc}1&1\\ 1&0\end{array}\right)\left(\begin{array}{cc}F_{n}&F_{n-1}\\ F_{n-1}&F_{n-2}\end{array}\right)
\end{align}
$$を$n$度繰りかえし用いることによって,
\begin{align}
&\left(\begin{array}{cc}L_1&L_0\\ L_0&L_{-1}\end{array}\right)=\left(\begin{array}{cc}1&2\\ 2&-1\end{array}\right),\\
&\left(\begin{array}{cc}F_1&F_0\\
F_0&F_{-1}\end{array}\right)=\left(\begin{array}{cc}1&0\\ 0&1\end{array}\right)
\end{align}の成立に帰結される. $\quad\Box$
行列$P$は逆行列を有する.
任意の$n\in\mathbb{Z}$について, 以下が成りたつ.
$\quad(1)\quad L_{n+1}L_{n-1}-L_n^2=5\cdot(-1)^{n+1}.$
$\quad(2)\quad F_{n+1}F_{n-1}-F_n^2=(-1)^n.$
行列表示の等式の両辺の行列式を比較すれば, 行列式の乗法性からこれらの等式が得られる. $\quad\Box$
任意の$n,k\in\mathbb{Z}$について, $F_n\mid F_{kn}$が成りたつ.
尚, ここで用いた記号$a\mid b$は整数$a$が整数$b$を割りきる整除関係を表し, $0\mid0$は成立するものとして認める.
$n=0$の場合は既に成立すると認めた. $n\neq0$のとき, 行列の各成分を$|F_n|$を法として見ると命題 1 から$P^n$は対角行列に合同であり, 従ってその冪である$P^{kn}$もまた対角行列と合同である. $P^{kn}$は$\left(\begin{array}{cc}F_{kn+1}&F_{kn}\\ F_{kn}&F_{kn-1}\end{array}\right)$とも書くことができるから, この行列の対角成分$F_{kn}$が$0$と合同であるということは$F_n\mid F_{kn}$が成立するということである. $\quad\Box$
任意の$m,n\in\mathbb{Z}$について, $\gcd(F_m,F_n)=F_{\gcd(m,n)}$が成りたつ.
ここで$\gcd(a,b)$は整数$a$と整数$b$の最大公約数を表し, $0$はあらゆる整数を約数に持つとして$\gcd(0,i)=\gcd(i,0)=i$と定めるが, $\gcd(0,0)$が$0$である点には注意を要する.
$F_{\gcd(m,n)}$と$\gcd(F_m,F_n)$が互いに整除しあう関係に在ることを証明する. 先ず, $F_{\gcd(m,n)}$が$F_m$と$F_n$の両方を割りきり従って$\gcd(F_m,F_n)$を割りきるということは, 先の命題 3 から明白な事である. 続いて$\gcd(m,n)=d$と置くと, 一次不定方程式$mA+nB=d$を充たす適当な整数$A,B$を取ることができ, 行列の関係式$P^d=(P^m)^A(P^n)^B$において右辺が法$\gcd(F_m,F_n)$によって対角行列と見なされることから$P^d$も同一の法において対角行列に合同である. $P^d$は$\left(\begin{array}{cc}F_{d+1}&F_d\\ F_d&F_{d-1}\end{array}\right)$とも書くことができるから, このとき$F_d$は法$\gcd(F_m,F_n)$において$0$と合同になるはずである. 故に, $F_{\gcd(m,n)}$と$\gcd(F_m,F_n)$は互いを互いの倍数として持つ関係であり, 然も二つは正であるから等しいことが判る. $\quad\Box$
任意の$m,n\in\mathbb{Z}$について, $|m|\neq2$の前提の下で$m\mid n\Longleftrightarrow F_m\mid F_n$が成りたつ.
(略).
同様にして, 以下の命題も証明することが可能である.
任意の$n,k\in\mathbb{Z}$について, $k$が奇数ならば$L_n\mid L_{kn}$が成りたつ.
任意の$m,n\in\mathbb{Z}$について, $m/\gcd(m,n)$と$n/\gcd(m,n)$が共に奇数ならば$\gcd(L_m,L_n)=L_{\gcd(m,n)}$が成りたつ.
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
