最強の迷路の攻略法「右手法(左手法)」とは・・・
大抵の迷路は、スタートから壁伝いでゴールすることができます。
これを右手法(左手法)と言います。
右手法(左手法)でゴールできる迷路の条件を調べました。
$$条件1. スタートとゴールは、迷路の一番外の壁にある$$
$$条件2. 迷路と四角形が同型である(スタートとゴールが外の壁の切れ目の場合、切れ目を繋げる)$$
$$迷路が条件1.2.を満たしている ⇒ スタートから壁伝いでゴールできる$$
以下のような迷路を指します。
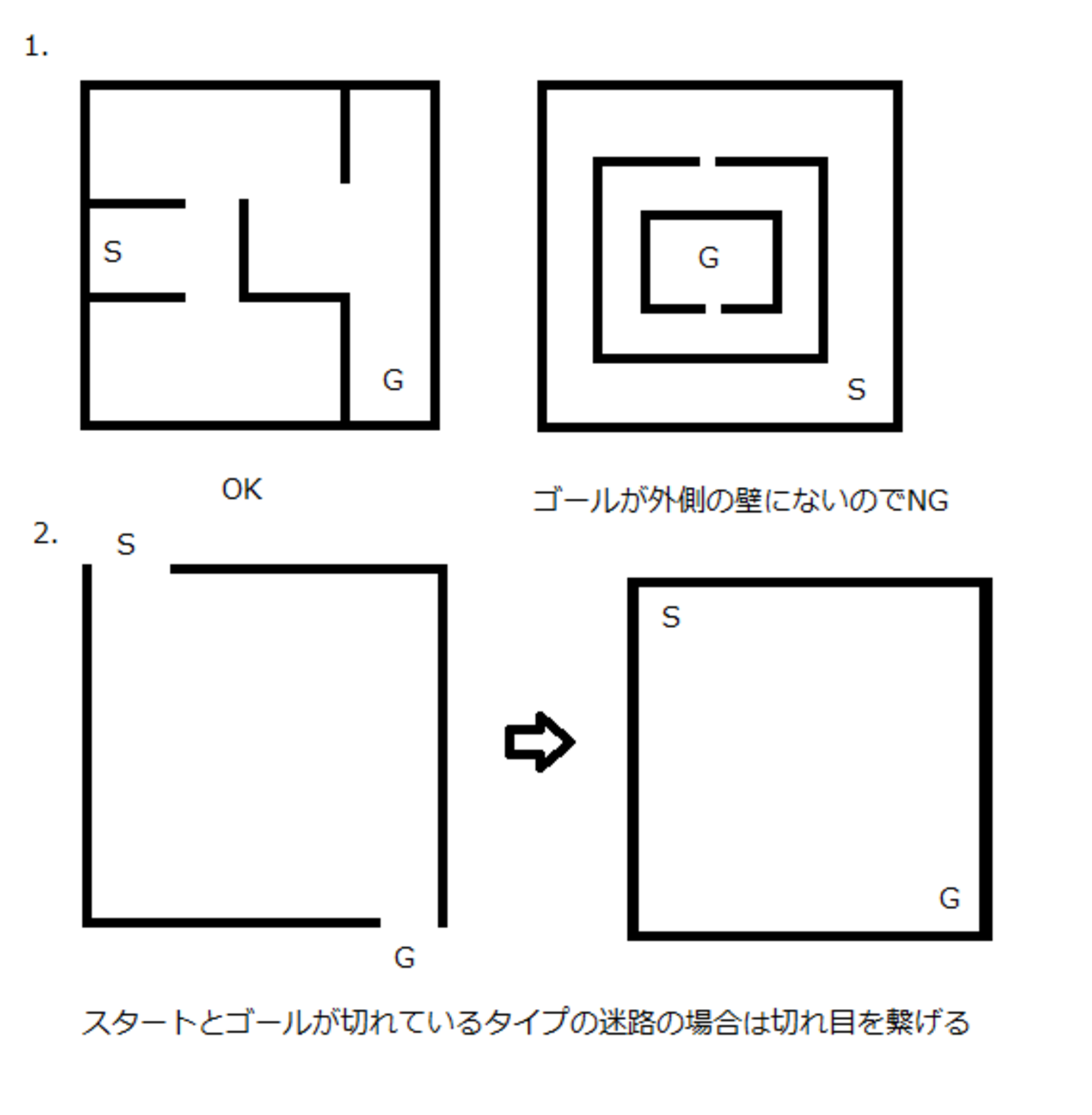壁伝いでゴールできる迷路
迷路と四角形は同型であるので、例えば右回りに迷路を進むということは、四角形を右回りに進むことと同じとなる。
四角形を一周するとスタートに戻るが、条件1. から、一周する間にゴールが必ず存在する。
よって、条件1.2.を満たす迷路は、壁伝いで必ずゴールができる。
補足
同型とは簡単に言うと、叩いたり延ばしたりすることで同じ形となることを言います。
ただし、境界があれば繋ぐことができません。
粘土を想像すると分かりやすいです。
例えば、粘土の取っ手付きマグカップを叩いて潰すと、トーラス(ドーナツ型)と同じ形になります。
このとき、マグカップとトーラスは同型といいます。
しかし、トーラスには穴が開いているので、それが境界となり、球には成り得ません。
このとき、トーラスと球は同型でないといいます。
他に
・レンズがない眼鏡のフレームは、穴が二つのトーラスと同型
・四角形と円は同型
・直方体と平面と直線と点は同型
・RPGの地図とトーラスは同型
ということが言えます。
RPGの地図とトーラスに関しては以下の記事をご覧ください。
RPGの世界は球ではなく...
しかし、平面と球の表面は同型ではありません。
これは、地球が地図で表現できないということを表しています。
追記(訂正のお詫び) 2021/5/8
サクラさんからご指摘を受けました。ありがとうございます。
例えば「口」と「曰」は位相同型でないとのことで、
確かにこれは正しく、僕の知識不足でした。申し訳ありませんでした。
なぜ位相同型ではないかと言うと、ここでは叩いて潰すという表現をしていますが、出っ張りは叩いて潰しても残ってしまうというイメージです。
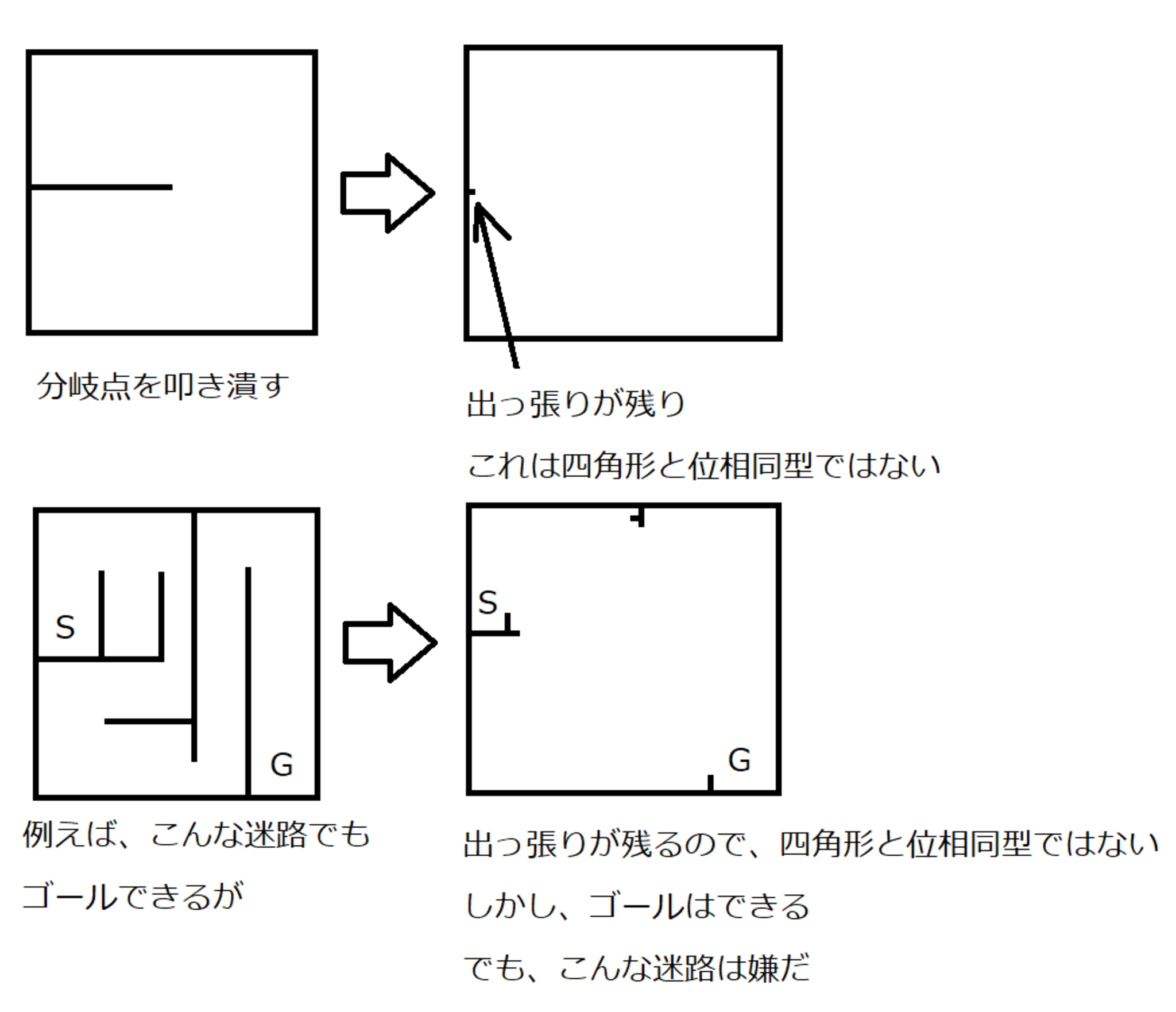出っ張りを残さなければ同型ではなくなる
詳しい証明はコメントしてくださってるので、そちらをご覧ください。
$$同型写像φ：曰→口 が存在すると仮定する$$
$$曰の連結部分をxとし、φ(x)=y \in 口とすると$$
$$φは同型写像なので$$
$$ \tilde{φ}：曰- \lbrace x \rbrace→口-\lbrace y \rbrace も同型$$
$$しかし、曰- \lbrace x \rbrace は二つの直線から成り、口-\lbrace y \rbraceは一つの直線からなるので矛盾$$
$$よって、「曰」と「口」は同型でない$$