無理数の最良近似分数と連分数展開・加比の理・ファレイ数列の関係(後編)
はじめに
この記事は
「
無理数の最良近似分数と連分数展開・加比の理・ファレイ数列の関係(前編)
」
の続きです。
当初の記事を書いた後、連分数展開から主近似分数を得る手法を改良して、近似する無理数の連分数展開さえあらかじめ分かっていれば、具体的な無理数の数値が不明であっても最良近似分数を得られる方法を見つけることができました。
この記事では、その方法を紹介します!
連分数展開を細分化すれば加比の理による分数列と一致する
その方法を紹介する前に、当初の記事投稿後に気が付いたことを書きます。
当初の記事投稿後、TokusiN さんのツイートを見て、「連分数展開から主近似分数を得る」アルゴリズムを細分化すれば加比の理による方法と一致することに気が付きました。
なお、ここからは見やすさのために連分数展開を次のように表記することとします。
$[2; 1, 2, 1, 1, 4, 1, 1, 6]=2+\dfrac{1}{1+\dfrac{1}{2+\dfrac{1}{1+\dfrac{1}{1+\dfrac{1}{4+\dfrac{1}{1+\dfrac{1}{1+\dfrac{1}{6}}}}}}}}$
さて、(前編)では連分数展開を止めて主近似分数を得るアルゴリズムは次の順番で行いました。
$[2; 1]=\frac{3}{1}$
$[2; 1, 2]=\frac{8}{3}$
$[2; 1, 2, 1]=\frac{11}{4}$
$[2; 1, 2, 1, 1]=\frac{19}{7}$
$[2; 1, 2, 1, 1, 4]=\frac{87}{32}$
$[2; 1, 2, 1, 1, 4, 1]=\frac{106}{39}$
$[2; 1, 2, 1, 1, 4, 1, 1]=\frac{193}{71}$
$[2; 1, 2, 1, 1, 4, 1, 1, 6]=\frac{1264}{465}$
これを末尾の数字を $1$ ずつ増やすように細分化するとこうなります。
$[2; 1]=\frac{3}{1}$
$[2; 1, 1]=\frac{5}{2}$
$[2; 1, 2]=\frac{8}{3}=\frac{3+5}{1+2}$
$[2; 1, 2, 1]=\frac{11}{4}=\frac{3+8}{1+3}$
$[2; 1, 2, 1, 1]=\frac{19}{7}=\frac{8+11}{3+4}$
$[2; 1, 2, 1, 1, 1]=\frac{30}{11}=\frac{11+19}{4+7}$
$[2; 1, 2, 1, 1, 2]=\frac{49}{18}=\frac{19+30}{7+11}$
$[2; 1, 2, 1, 1, 3]=\frac{68}{25}=\frac{19+49}{7+18}$
$[2; 1, 2, 1, 1, 4]=\frac{87}{32}=\frac{19+68}{7+25}$
$[2; 1, 2, 1, 1, 4, 1]=\frac{106}{39}=\frac{19+87}{7+32}$
$[2; 1, 2, 1, 1, 4, 1, 1]=\frac{193}{71}=\frac{87+106}{32+39}$
$[2; 1, 2, 1, 1, 4, 1, 1, 1]=\frac{299}{110}=\frac{106+193}{39+71}$
$[2; 1, 2, 1, 1, 4, 1, 1, 2]=\frac{492}{181}=\frac{193+299}{71+110}$
$[2; 1, 2, 1, 1, 4, 1, 1, 3]=\frac{685}{252}=\frac{193+492}{71+181}$
$[2; 1, 2, 1, 1, 4, 1, 1, 4]=\frac{878}{323}=\frac{193+685}{71+252}$
$[2; 1, 2, 1, 1, 4, 1, 1, 5]=\frac{1071}{394}=\frac{193+878}{71+323}$
$[2; 1, 2, 1, 1, 4, 1, 1, 6]=\frac{1264}{465}=\frac{193+1071}{71+394}$
この方法で得られる分数を見ると、なんと加比の理で得られる分数たちと完全に一致しています!これは驚きました。このことを踏まえて対応表を作り直すとこんな感じになります。
| 加比の理 | 連分数展開 | 第1種最良近似分数 |
|---|---|---|
| $e<\dfrac{3}{1}$ | $[2;1]$ | Y |
| $\dfrac{5}{2}< e$ | $[2;1,1]$ | Y |
| $\dfrac{8}{3}< e$ | $[2;1,2]$ | Y |
| $e<\dfrac{11}{4}$ | $[2;1,2,1]$ | Y |
| $\dfrac{19}{7}< e$ | $[2;1,2,1,1]$ | Y |
| $e<\dfrac{30}{11}$ | $[2;1,2,1,1,1]$ | - |
| $e<\dfrac{49}{18}$ | $[2;1,2,1,1,2]$ | Y |
| $e<\dfrac{68}{25}$ | $[2;1,2,1,1,3]$ | Y |
| $e<\dfrac{87}{32}$ | $[2;1,2,1,1,4]$ | Y |
| $\dfrac{106}{39}< e$ | $[2;1,2,1,1,4,1]$ | Y |
| $e<\dfrac{193}{71}$ | $[2;1,2,1,1,4,1,1]$ | Y |
| $\dfrac{299}{110}< e$ | $[2;1,2,1,1,4,1,1,1]$ | - |
| $\dfrac{492}{181}< e$ | $[2;1,2,1,1,4,1,1,2]$ | - |
| $\dfrac{685}{252}< e$ | $[2;1,2,1,1,4,1,1,3]$ | Y |
| $\dfrac{878}{323}< e$ | $[2;1,2,1,1,4,1,1,4]$ | Y |
| $\dfrac{1071}{394}< e$ | $[2;1,2,1,1,4,1,1,5]$ | Y |
| $\dfrac{1264}{465}< e$ | $[2;1,2,1,1,4,1,1,6]$ | Y |
こうして並べてみると、$e$ に下から近づくか上から近づくかが入れ替わるときに連分数が１段階増えることや、その直前に第2種最良近似分数となることがわかります。また、入れ替わらない場合には、「途中から第1種最良近似分数に切り替わる」という法則があります。
主近似分数と中間近似分数
このように、連分数の末尾の分母を1ずつ変化させて得られる近似分数を特に「中間近似分数」と呼びます。
例えば、上の中間近似分数たちのうち $[2;1,2,1,1,4,1,1,3]$ は「3番目の8次中間近似分数」のように呼びます。8次中間近似分数は1番目～5番目まであり、そのうち3番目ということですね。
主近似分数は中間近似分数には含まれません。
「中間近似分数」の名称は参考文献の「木村 俊一, 連分数のふしぎ, BLUE BACKS, 講談社」で使われています。
主近似分数が $e$ に近づいていく様子はこのようになります。
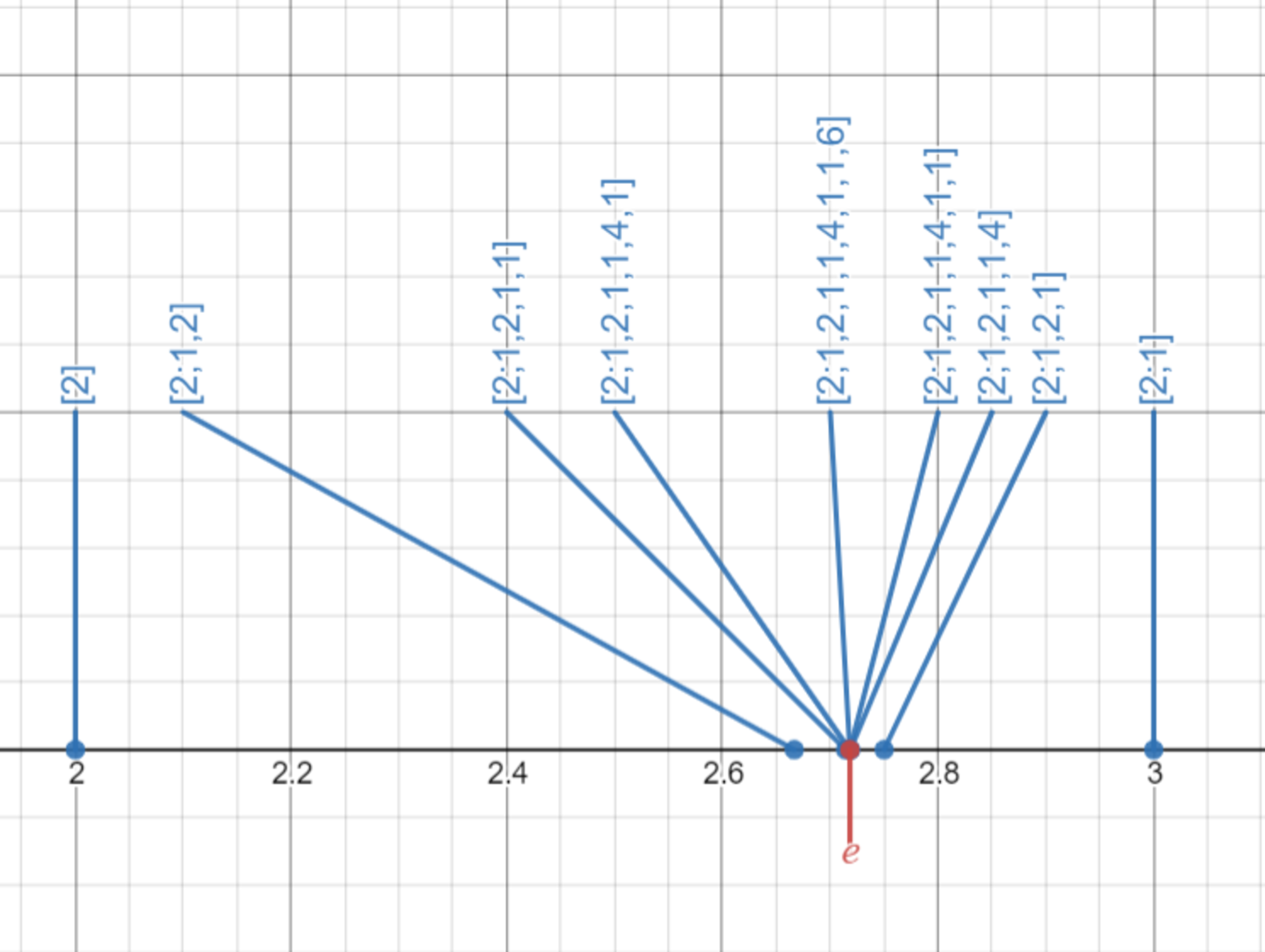主近似分数は上下から交互に近づいていく
上下から交互に近づいていくことがわかります。
そして、中間近似分数が $e$ に近づいていく様子はこのようになります。
中間近似分数は同じ方向から少しずつ近づいていく
同じ方向へ少しずつ近づいていくことがわかります。
ここで、中間近似分数が第1種最良近似分数になっているかどうかを考えてみましょう。
ファレイ数列で考えると、それぞれの中間近似分数を「$\dfrac{\text{分子}}{\text{分母
}}$」の形式で表したとき、近似する無理数との間にはその分母より小さい分母を持つような近似分数は存在しないことがわかります((前編)参照)。
ということは、近似する無理数の反対側にある、直前の主近似分数と比較して、より誤差が小さければ第１種最良近似分数であることがわかります。
図2でいうと、
$[2;1,2,1,1,4,1,1,1]$
$[2;1,2,1,1,4,1,1,2]$
は
$[2;1,2,1,1,4,1,1]$
よりも誤差が大きいので第１種最良近似分数ではありません。
$[2;1,2,1,1,4,1,1,4]$
$[2;1,2,1,1,4,1,1,5]$
$[2;1,2,1,1,4,1,1,6]$
は
$[2;1,2,1,1,4,1,1]$
よりも誤差が小さいので第1種最良近似分数です。
$[2;1,2,1,1,4,1,1,3]$
は微妙な位置ですね。
実は、$e$ の連分数展開があらかじめわかっていれば、$e$ の具体的な値を使わなくてもどちらが $e$ に近いのかを判定することができます。
連分数の大小関係
どちらが $e$ に近いのかの判定方法を紹介する前に、連分数の大小関係を判定する方法を紹介します。
次数
まず、連分数の長さを「●次」と表現することにします。
たとえば
$[2]$……$0$次
$[2;1]$……$1$次
$[2;1,2]$……$2$次
$[2;1,2,1]$……$3$次
$[2;1,2,1,1]$……$4$次
$[2;1,2,1,1,4]$……$5$次
となります。
大小判定
例えば、$[0;1,1,1,2,1,5,4]$ と $[0;1,1,1,3,3,2,1]$ の大小関係を判定したいとしましょう。
次数が $1$ 増えるたびに、最後の数字の大小関係への影響は逆転しますから、次数の偶奇に注目することで大小を判定することができます。
2つの連分数展開に現れる数字を次数の低い方から比較していき、最初に異なる数字となったとき、それぞれの数字を$a,b$とする。
$\fbox{1}$ 奇数次のとき
$a< b \qquad \Rightarrow \qquad [\cdots ,a,\cdots]>[\cdots ,b,\cdots]$
$\fbox{2}$ 偶数次のとき
$a< b \qquad \Rightarrow \qquad [\cdots ,a,\cdots]<[\cdots ,b,\cdots]$
$[0;1,1,1,2,1,5,4]$ と $[0;1,1,1,3,3,2,1]$ の場合、最初に異なる数字となるのは $4$ 次で、偶数次ですから、$2<3$ より
$[0;1,1,1,2,1,5,4]<[0;1,1,1,3,3,2,1]$
とわかります。
検算してみると、
$[0;1,1,1,2,1,5,4]=\dfrac{167}{263}=0.634981\cdots$
$[0;1,1,1,3,3,2,1]=\dfrac{76}{119}=0.638655\cdots$
で、確かにあっています。
中間近似分数のさらに半分になる連分数
次に、主近似分数と中間近似分数の平均値となる連分数展開が簡単にわかる次のような法則があります。
$n$ 次連分数 $B$ の末尾に数字を$1$つ追加した $(n+1)$ 次連分数を $A$ とし、連分数 $A$ に対して、最後に追加した $(n+1)$ 次の数字を $2$ 倍にして $1$ 次～ $(n+1)$ 次の数字の並びを反転させて追加した連分数を $C$ とすると、
$\dfrac{A+B}{2}=C$
が成り立つ。
この式は
TokusiNさんのツイート
で教えてもらった式で、
tria_math
さんに証明していただきました。
証明は
tria_math
さんの記事をご覧ください。
具体例
例えば、
$A=[0;1,1,3,2,3,4]$
$B=[0;1,1,3,2,3]$
から $C$ を作ると
$C=[0;\underbrace{1,1,3,2,3}_{\text{そのまま}},\underbrace{8}_{2\text{倍}},\underbrace{3,2,3,1,1}_{\text{反転}}]$
となります。
検算すると
$A=\dfrac{133}{236}$
$B=\dfrac{31}{55}$
$C=\dfrac{14631}{25960}$
$\dfrac{A+B}{2}=C$
となり、確かに成り立っています。
具体的判定法
これを使えば、主近似分数と中間近似分数の平均値となる連分数展開が、近似する無理数の連分数展開より大きいか小さいかを比較することで、「主近似分数と中間近似分数のどちらがより誤差が小さいか」を判定することができるというわけです。
先ほどの
$[2;1,2,1,1,4,1,1,3]$
を例に実際にやってみましょう。
$A=[2;1,2,1,1,4,1,1,3]$
$B=[2;1,2,1,1,4,1,1]$
から $C$ を作ると
$C=[2;\underbrace{1,2,1,1,4,1,1}_{\text{そのまま}},\underbrace{6}_{2\text{倍}},\underbrace{1,1,4,1,1,2,1}_{\text{反転}}]$
となります。これを $e$ の連分数展開と比べてどちらが大きいか判定します。
そのために、$e$ の連分数展開を使います。
$e$ の連分数展開は無限に続きますが、次のように規則的に数字が並ぶことがわかっています。
$\begin{align} e&=[2; 1, 2, 1, 1, 4, 1, 1, 6,1,1,8,1,1,\cdots]\\ &=2+\dfrac{1}{1+\dfrac{1}{2+\dfrac{1}{1+\dfrac{1}{1+\dfrac{1}{4+\dfrac{1}{1+\dfrac{1}{1+\dfrac{1}{6+\dfrac{1}{1+\dfrac{1}{1+\dfrac{1}{8+\cdots}}}}}}}}}}} \end{align}$
$C$ と $e$ を先ほどの判定法で大小比較します。$C$ と $e$ は $10$ 次までは同じで、$11$ 次で数字が異なります。奇数次ですね。$11$ 次の数字を比較すれば
$2<8$
より
$C > e$
とわかります。
$C=\dfrac{A+B}{2}$
ですから
$A< e<\dfrac{A+B}{2}< B$
となり、$A$ の方が $B$ よりも $e$ に近いこと、つまり $A$ は第1種最良近似分数であることがわかりましたね!
$e$ の最良近似分数をどんどん作る
この方法を使って第1種最良近似分数をどんどん得ることができます!
$[2; 1]=\frac{3}{1}$
$[2; 1, 1]=\frac{5}{2}$
$[2; 1, 2]=\frac{8}{3}$
$[2; 1, 2, 1]=\frac{11}{4}$
$[2; 1, 2, 1, 1]=\frac{19}{7}$
$[2; 1, 2, 1, 1, 2]=\frac{49}{18}$
$[2; 1, 2, 1, 1, 3]=\frac{68}{25}$
$[2; 1, 2, 1, 1, 4]=\frac{87}{32}$
$[2; 1, 2, 1, 1, 4, 1]=\frac{106}{39}$
$[2; 1, 2, 1, 1, 4, 1, 1]=\frac{193}{71}$
$[2; 1, 2, 1, 1, 4, 1, 1, 3]=\frac{685}{252}$
$[2; 1, 2, 1, 1, 4, 1, 1, 4]=\frac{878}{323}$
$[2; 1, 2, 1, 1, 4, 1, 1, 5]=\frac{1071}{394}$
$[2; 1, 2, 1, 1, 4, 1, 1, 6]=\frac{1264}{465}$
$\qquad\vdots$
おわりに
今回の方法は TokusiNさんのツイート をベースにしています。また、私には証明できなかった部分は tria_math さんに証明していただきました。ありがとうございました。
連分数展開で主近似分数(=第2種最良近似分数)を得られることはご存じでしたでしょうか。また、連分数展開で最良近似分数(の一部)が得られることは知っていても、連分数展開では得られない最良近似分数(第1種最良近似分数であって第2種最良近似分数でないもの)があることは知らなかったという人もいるのではないでしょうか。
今回、任意の無理数の最良近似分数を加比の理で得る方法がわかりました。なかなか面白いと思います。
最後に、今回の手法を使って黄金比
$\phi=\dfrac{1+\sqrt{5}}{2}=1.6180339\cdots$
で順に最良近似分数を求めてみてください。何か面白いことがおきるかもしれませんよ？
参考文献
この記事を高評価した人
この記事に送られたバッジ
投稿者
