[ラビットチャレンジ] 深層学習day2 レポート

はじめに

本稿は、E資格の受験資格の取得を目的としたラビットチャレンジの受講に伴うレポート記事である。

Section1：勾配消失問題

復習

誤差逆伝播法

計算結果（=誤差）から微分を逆算することで、不要な再帰的計算を避けて微分を算出できる。

■確認テスト
連鎖律の原理を使い、$dz/dx$を求めよ。
\begin{align} z &= t^2 \\ t &= x + y \end{align}

〇解答
まずは以下の通り。
\begin{align} \frac{dz}{dt} &= 2t \\ \frac{dt}{dx} &= 1 \end{align}

連鎖律より、以下が成り立つ。
\begin{align} \frac{dz}{dx} &= \frac{dz}{dt} \frac{dt}{dx} = 2t \times 1 \\ &= 2t = 2(x + y) \end{align}

勾配消失問題

誤差逆伝播法が下位層に進んでいくに連れて、勾配がどんどん緩やかになっていく。
そのため、勾配降下法による、更新では下位層のパラメータはほとんど変わらず、訓練は最適値に収束しなくなる。

活性化関数として、シグモイド関数を採用すると、大きな値では出力の変化が微小なため、勾配消失問題を引き起こす事がある。

■確認テスト
シグモイド関数は以下の$f(u)$であった。
\begin{align} f(u) = \frac{1}{1 + \exp(-u)} \end{align}

$f'(0)$を求めよ。

〇解答

\begin{align} f'(u) &= -\frac{(1 + \exp(-u))'}{(1 + \exp(-u))^2} \\ &= \frac{\exp(-u)}{(1 + \exp(-u))^2} \end{align}

よって、$f'(0) = \exp(0)/(1 + \exp(0))^2 = 1/4 = 0.25$となる。

なお、式変形をすることで、以下の通り表すこともできる。
\begin{align} f'(u) &= (1 - f(u)) f(u) \end{align}

勾配消失の解決方法

• 活性化関数の選択
• 重みの初期値設定
• バッチ正規化

活性化関数の選択

ReLU関数を採用する。

• 最近では最も使われている活性化関数
• 勾配消失問題の回避とスパース化に貢献

ReLU関数は day1 レポート を参照。

重みの初期値設定

Xavier

Xavierの初期値を設定する際の活性化関数

• ReLU関数
• シグモイド(ロジスティック)関数
• 双曲線正接関数($\tanh$関数)

初期値の設定として、重みの要素を、前の層のノード数の平方根で除算した値を用いる。

          # Xavierの初期値
    network['W1'] = np.random.randn(input_layer_size, hidden_layer_size) / (np.sqrt(input_layer_size))
    network['W2'] = np.random.randn(hidden_layer_size, output_layer_size) / (np.sqrt(hidden_layer_size))
    

He

Heの初期値を設定する際の活性化関数

• Relu関数

初期値の設定として、重みの要素を、前の層のノード数の平方根で除算した値に対し$\sqrt{2}$をかけ合わせた値を用いる。

          # Heの初期値
    network['W1'] = np.random.randn(input_layer_size, hidden_layer_size) / np.sqrt(input_layer_size) * np.sqrt(2)
    network['W2'] = np.random.randn(hidden_layer_size, output_layer_size) / np.sqrt(hidden_layer_1_size) * np.sqrt(2)
    

■確認テスト
重みの初期値に0を設定すると、どのような問題が発生するか。簡潔に説明せよ。

〇解答
正しい学習が行えなくなる。
すべての重みの値が均一に更新されることから、重みをもつ意味そのものがなくなってしまう。

バッチ正規化

ミニバッチ単位で、入力値のデータの偏りを抑制する方法のこと。

バッチ正規化の使い所としては、活性化関数に値を渡す前後に、バッチ正規化の処理を孕んだ層を加える。

バッチ正規化層への入力値は$u^{(l)} = w^{(l)} z^{(l-1)} + b^{(l)}$または$z$を用いる。

■確認テスト
一般的に考えられるバッチ正規化の効果を2点挙げよ。

〇解答

• 勾配消失問題が起きにくくなる。
• 学習の高速化や過学習の抑制につながる。

実装演習

初期値：ガウシアン、活性化関数：シグモイド関数の例

      import numpy as np
from common import layers
from collections import OrderedDict
from common import functions
from data.mnist import load_mnist
import matplotlib.pyplot as plt

# mnistをロード
(x_train, d_train), (x_test, d_test) = load_mnist(normalize=True, one_hot_label=True)
train_size = len(x_train)

print("データ読み込み完了")

# 重み初期値補正係数
wieght_init = 0.01
#入力層サイズ
input_layer_size = 784
#中間層サイズ
hidden_layer_1_size = 40
hidden_layer_2_size = 20

#出力層サイズ
output_layer_size = 10
# 繰り返し数
iters_num = 2000
# ミニバッチサイズ
batch_size = 100
# 学習率
learning_rate = 0.1
# 描写頻度
plot_interval=10

# 初期設定
def init_network():
    network = {} 
    network['W1'] = wieght_init * np.random.randn(input_layer_size, hidden_layer_1_size)
    network['W2'] = wieght_init * np.random.randn(hidden_layer_1_size, hidden_layer_2_size)
    network['W3'] = wieght_init * np.random.randn(hidden_layer_2_size, output_layer_size)

    network['b1'] = np.zeros(hidden_layer_1_size)
    network['b2'] = np.zeros(hidden_layer_2_size)
    network['b3'] = np.zeros(output_layer_size)

    return network

# 順伝播
def forward(network, x):
    W1, W2, W3 = network['W1'], network['W2'], network['W3']
    b1, b2, b3 = network['b1'], network['b2'], network['b3']
    hidden_f = functions.sigmoid
    
    u1 =  np.dot(x, W1) + b1
    z1 = hidden_f(u1)
    u2 =  np.dot(z1, W2) + b2
    z2 = hidden_f(u2)
    u3 =  np.dot(z2, W3) + b3
    y = functions.softmax(u3)
 
    return z1, z2, y

# 誤差逆伝播
def backward(x, d, z1, z2, y):
    grad = {}
    
    W1, W2, W3 = network['W1'], network['W2'], network['W3']
    b1, b2, b3 = network['b1'], network['b2'], network['b3']
    hidden_d_f = functions.d_sigmoid
    last_d_f = functions.d_softmax_with_loss
    
    
    # 出力層でのデルタ
    delta3 = last_d_f(d, y)
    # b3の勾配
    grad['b3'] = np.sum(delta3, axis=0)
    # W3の勾配
    grad['W3'] = np.dot(z2.T, delta3)
    # 2層でのデルタ
    delta2 = np.dot(delta3, W3.T) * hidden_d_f(z2)
    # b2の勾配
    grad['b2'] = np.sum(delta2, axis=0)
    # W2の勾配
    grad['W2'] = np.dot(z1.T, delta2)
    # 1層でのデルタ
    delta1 = np.dot(delta2, W2.T) * hidden_d_f(z1)
    # b1の勾配
    grad['b1'] = np.sum(delta1, axis=0)
    # W1の勾配
    grad['W1'] = np.dot(x.T, delta1)

    return grad

# パラメータの初期化
network = init_network()

accuracies_train = []
accuracies_test = []

# 正答率
def accuracy(x, d):
    z1, z2, y = forward(network, x)
    y = np.argmax(y, axis=1)
    if d.ndim != 1 : d = np.argmax(d, axis=1)
    accuracy = np.sum(y == d) / float(x.shape[0])
    return accuracy

for i in range(iters_num):
    # ランダムにバッチを取得    
    batch_mask = np.random.choice(train_size, batch_size)
    # ミニバッチに対応する教師訓練画像データを取得    
    x_batch = x_train[batch_mask]
    # ミニバッチに対応する訓練正解ラベルデータを取得する
    d_batch = d_train[batch_mask]


    
    z1, z2, y = forward(network, x_batch)
    grad = backward(x_batch, d_batch, z1, z2, y)

    if (i+1)%plot_interval==0:
        accr_test = accuracy(x_test, d_test)
        accuracies_test.append(accr_test)
        
        accr_train = accuracy(x_batch, d_batch)
        accuracies_train.append(accr_train)

        print('Generation: ' + str(i+1) + '. 正答率(トレーニング) = ' + str(accr_train))
        print('                : ' + str(i+1) + '. 正答率(テスト) = ' + str(accr_test))

    # パラメータに勾配適用
    for key in ('W1', 'W2', 'W3', 'b1', 'b2', 'b3'):
        network[key]  -= learning_rate * grad[key]


lists = range(0, iters_num, plot_interval)
plt.plot(lists, accuracies_train, label="training set")
plt.plot(lists, accuracies_test,  label="test set")
plt.legend(loc="lower right")
plt.title("accuracy")
plt.xlabel("count")
plt.ylabel("accuracy")
plt.ylim(0, 1.0)
# グラフの表示
plt.show()
    

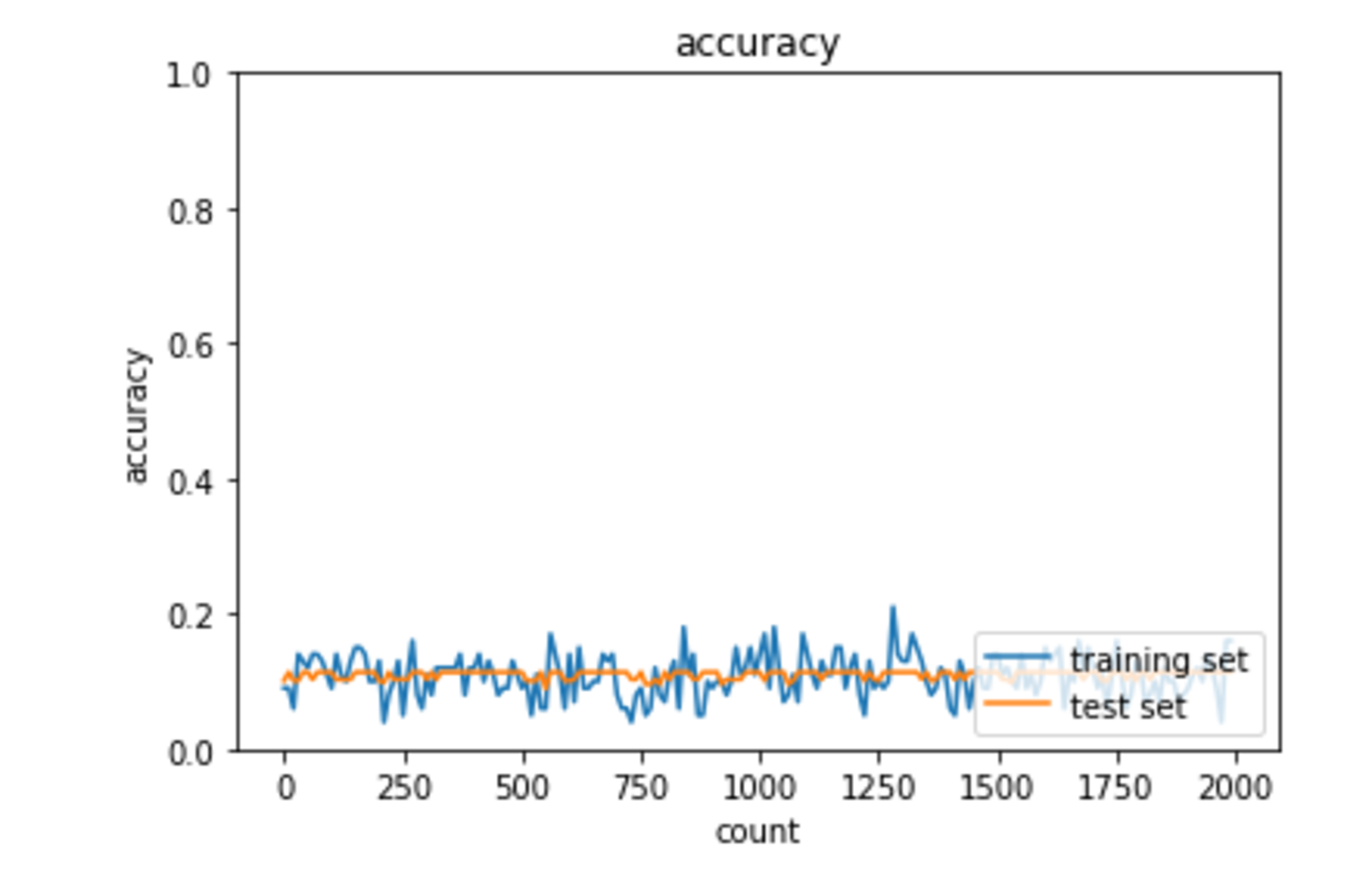
思うように学習が進んでいないように見受けられる。

活性化関数:ReLUの例

      import numpy as np
from data.mnist import load_mnist
from PIL import Image
import pickle
from common import functions
import matplotlib.pyplot as plt

# mnistをロード
(x_train, d_train), (x_test, d_test) = load_mnist(normalize=True, one_hot_label=True)
train_size = len(x_train)

print("データ読み込み完了")

# 重み初期値補正係数
wieght_init = 0.01
#入力層サイズ
input_layer_size = 784
#中間層サイズ
hidden_layer_1_size = 40
hidden_layer_2_size = 20

#出力層サイズ
output_layer_size = 10
# 繰り返し数
iters_num = 2000
# ミニバッチサイズ
batch_size = 100
# 学習率
learning_rate = 0.1
# 描写頻度
plot_interval=10

# 初期設定
def init_network():
    network = {} 

    network['W1'] = wieght_init * np.random.randn(input_layer_size, hidden_layer_1_size)
    network['W2'] = wieght_init * np.random.randn(hidden_layer_1_size, hidden_layer_2_size)
    network['W3'] = wieght_init * np.random.randn(hidden_layer_2_size, output_layer_size)
            
    network['b1'] = np.zeros(hidden_layer_1_size)
    network['b2'] = np.zeros(hidden_layer_2_size)
    network['b3'] = np.zeros(output_layer_size)

    return network

# 順伝播
def forward(network, x):
    W1, W2, W3 = network['W1'], network['W2'], network['W3']
    b1, b2, b3 = network['b1'], network['b2'], network['b3']
    
    ###########  変更箇所  ##############

    hidden_f = functions.relu

    #################################
    
    u1 =  np.dot(x, W1) + b1
    z1 = hidden_f(u1)
    u2 =  np.dot(z1, W2) + b2
    z2 = hidden_f(u2)
    u3 =  np.dot(z2, W3) + b3
    y = functions.softmax(u3)
 
    return z1, z2, y

# 誤差逆伝播
def backward(x, d, z1, z2, y):
    grad = {}
    
    W1, W2, W3 = network['W1'], network['W2'], network['W3']
    b1, b2, b3 = network['b1'], network['b2'], network['b3']

    ###########  変更箇所  ##############
    
    hidden_d_f = functions.d_relu
    
    #################################
    
    
    # 出力層でのデルタ
    delta3 = functions.d_softmax_with_loss(d, y)
    # b3の勾配
    grad['b3'] = np.sum(delta3, axis=0)
    # W3の勾配
    grad['W3'] = np.dot(z2.T, delta3)
    # 2層でのデルタ
    delta2 = np.dot(delta3, W3.T) * hidden_d_f(z2)
    # b2の勾配
    grad['b2'] = np.sum(delta2, axis=0)
    # W2の勾配
    grad['W2'] = np.dot(z1.T, delta2)
    # 1層でのデルタ
    delta1 = np.dot(delta2, W2.T) * hidden_d_f(z1)
    # b1の勾配
    grad['b1'] = np.sum(delta1, axis=0)
    # W1の勾配
    grad['W1'] = np.dot(x.T, delta1)

    return grad

# パラメータの初期化
network = init_network()

accuracies_train = []
accuracies_test = []

# 正答率
def accuracy(x, d):
    z1, z2, y = forward(network, x)
    y = np.argmax(y, axis=1)
    if d.ndim != 1 : d = np.argmax(d, axis=1)
    accuracy = np.sum(y == d) / float(x.shape[0])
    return accuracy

for i in range(iters_num):
    # ランダムにバッチを取得    
    batch_mask = np.random.choice(train_size, batch_size)
    # ミニバッチに対応する教師訓練画像データを取得    
    x_batch = x_train[batch_mask]
    # ミニバッチに対応する訓練正解ラベルデータを取得する
    d_batch = d_train[batch_mask]


    
    z1, z2, y = forward(network, x_batch)
    grad = backward(x_batch, d_batch, z1, z2, y)

    if (i+1)%plot_interval==0:
        accr_test = accuracy(x_test, d_test)
        accuracies_test.append(accr_test)
        
        accr_train = accuracy(x_batch, d_batch)
        accuracies_train.append(accr_train)

        print('Generation: ' + str(i+1) + '. 正答率(トレーニング) = ' + str(accr_train))
        print('                : ' + str(i+1) + '. 正答率(テスト) = ' + str(accr_test))
        
    # パラメータに勾配適用
    for key in ('W1', 'W2', 'W3', 'b1', 'b2', 'b3'):
        network[key]  -= learning_rate * grad[key]


lists = range(0, iters_num, plot_interval)
plt.plot(lists, accuracies_train, label="training set")
plt.plot(lists, accuracies_test,  label="test set")
plt.legend(loc="lower right")
plt.title("accuracy")
plt.xlabel("count")
plt.ylabel("accuracy")
plt.ylim(0, 1.0)
# グラフの表示
plt.show()
    

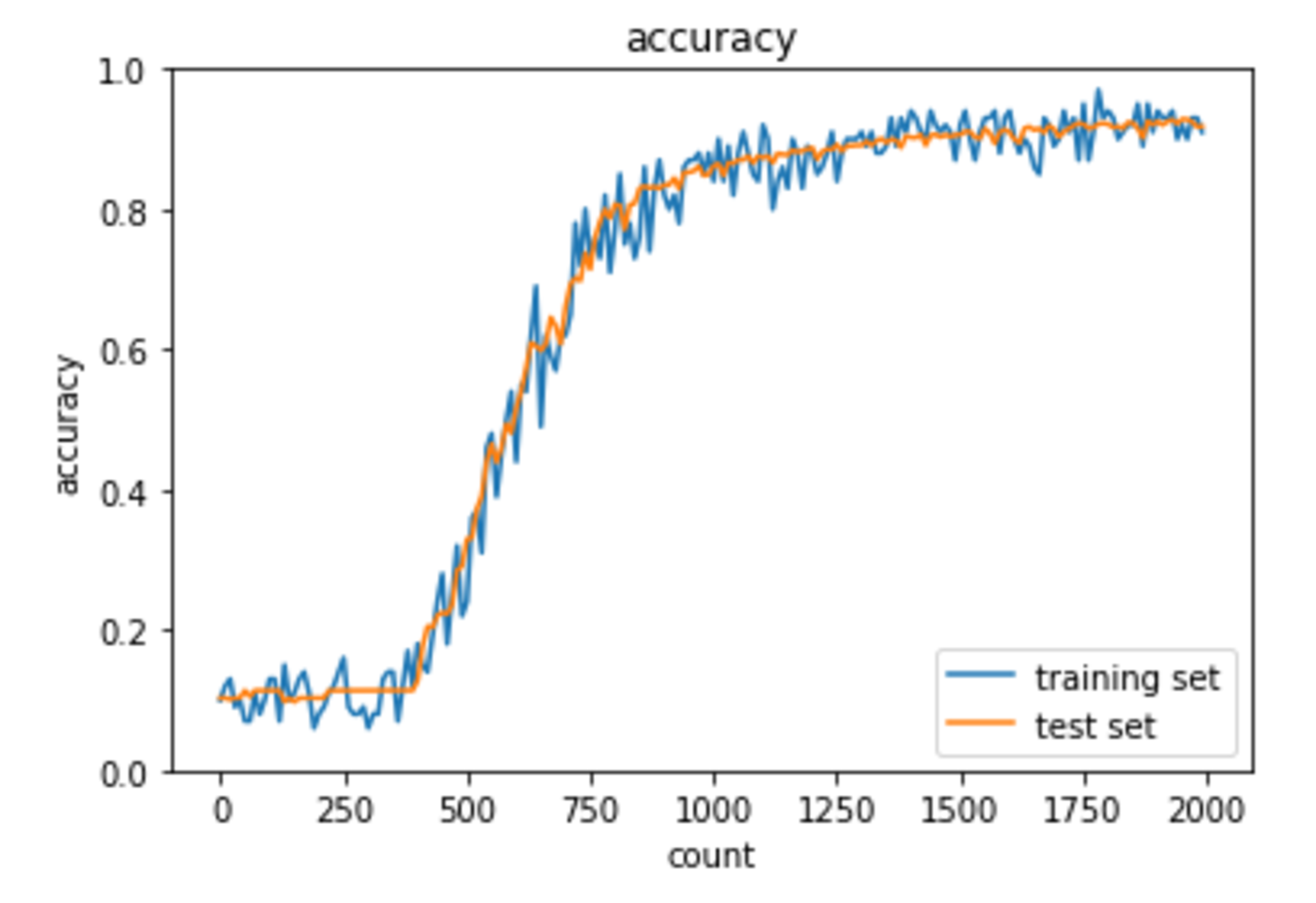
先ほどとは異なり、うまく学習が進んでいるように見受けられる。

活性化関数：シグモイド関数、初期値Xavier

      import numpy as np
from data.mnist import load_mnist
from PIL import Image
import pickle
from common import functions
import matplotlib.pyplot as plt

# mnistをロード
(x_train, d_train), (x_test, d_test) = load_mnist(normalize=True, one_hot_label=True)
train_size = len(x_train)

print("データ読み込み完了")

#入力層サイズ
input_layer_size = 784
#中間層サイズ
hidden_layer_1_size = 40
hidden_layer_2_size = 20
#出力層サイズ
output_layer_size = 10
# 繰り返し数
iters_num = 2000
# ミニバッチサイズ
batch_size = 100
# 学習率
learning_rate = 0.1
# 描写頻度
plot_interval=10

# 初期設定
def init_network():
    network = {} 
    
    ###########  変更箇所  ##############
    
    # Xavierの初期値
    network['W1'] = np.random.randn(input_layer_size, hidden_layer_1_size) / (np.sqrt(input_layer_size))
    network['W2'] = np.random.randn(hidden_layer_1_size, hidden_layer_2_size) / (np.sqrt(hidden_layer_1_size))
    network['W3'] = np.random.randn(hidden_layer_2_size, output_layer_size) / (np.sqrt(hidden_layer_2_size))
    
    #################################
    
    network['b1'] = np.zeros(hidden_layer_1_size)
    network['b2'] = np.zeros(hidden_layer_2_size)
    network['b3'] = np.zeros(output_layer_size)

    return network

# 順伝播
def forward(network, x):
    W1, W2, W3 = network['W1'], network['W2'], network['W3']
    b1, b2, b3 = network['b1'], network['b2'], network['b3']
    hidden_f = functions.sigmoid
    
    u1 =  np.dot(x, W1) + b1
    z1 = hidden_f(u1)
    u2 =  np.dot(z1, W2) + b2
    z2 = hidden_f(u2)
    u3 =  np.dot(z2, W3) + b3
    y = functions.softmax(u3)
 
    return z1, z2, y

# 誤差逆伝播
def backward(x, d, z1, z2, y):
    grad = {}
    
    W1, W2, W3 = network['W1'], network['W2'], network['W3']
    b1, b2, b3 = network['b1'], network['b2'], network['b3']
    hidden_d_f = functions.d_sigmoid
    
    # 出力層でのデルタ
    delta3 = functions.d_softmax_with_loss(d, y)
    # b3の勾配
    grad['b3'] = np.sum(delta3, axis=0)
    # W3の勾配
    grad['W3'] = np.dot(z2.T, delta3)
    # 2層でのデルタ
    delta2 = np.dot(delta3, W3.T) * hidden_d_f(z2)
    # b2の勾配
    grad['b2'] = np.sum(delta2, axis=0)
    # W2の勾配
    grad['W2'] = np.dot(z1.T, delta2)
    # 1層でのデルタ
    delta1 = np.dot(delta2, W2.T) * hidden_d_f(z1)
    # b1の勾配
    grad['b1'] = np.sum(delta1, axis=0)
    # W1の勾配
    grad['W1'] = np.dot(x.T, delta1)

    return grad

# パラメータの初期化
network = init_network()

accuracies_train = []
accuracies_test = []

# 正答率
def accuracy(x, d):
    z1, z2, y = forward(network, x)
    y = np.argmax(y, axis=1)
    if d.ndim != 1 : d = np.argmax(d, axis=1)
    accuracy = np.sum(y == d) / float(x.shape[0])
    return accuracy

for i in range(iters_num):
    # ランダムにバッチを取得    
    batch_mask = np.random.choice(train_size, batch_size)
    # ミニバッチに対応する教師訓練画像データを取得    
    x_batch = x_train[batch_mask]
    # ミニバッチに対応する訓練正解ラベルデータを取得する
    d_batch = d_train[batch_mask]


    
    z1, z2, y = forward(network, x_batch)
    grad = backward(x_batch, d_batch, z1, z2, y)

    if (i+1)%plot_interval==0:
        accr_test = accuracy(x_test, d_test)
        accuracies_test.append(accr_test)
        
        accr_train = accuracy(x_batch, d_batch)
        accuracies_train.append(accr_train)

        print('Generation: ' + str(i+1) + '. 正答率(トレーニング) = ' + str(accr_train))
        print('                : ' + str(i+1) + '. 正答率(テスト) = ' + str(accr_test))
        
    # パラメータに勾配適用
    for key in ('W1', 'W2', 'W3', 'b1', 'b2', 'b3'):
        network[key]  -= learning_rate * grad[key]


lists = range(0, iters_num, plot_interval)
plt.plot(lists, accuracies_train, label="training set")
plt.plot(lists, accuracies_test,  label="test set")
plt.legend(loc="lower right")
plt.title("accuracy")
plt.xlabel("count")
plt.ylabel("accuracy")
plt.ylim(0, 1.0)
# グラフの表示
plt.show()
    

活性化関数：ReLU関数、初期値：Heの例

      import numpy as np
from data.mnist import load_mnist
from PIL import Image
import pickle
from common import functions
import matplotlib.pyplot as plt

# mnistをロード
(x_train, d_train), (x_test, d_test) = load_mnist(normalize=True, one_hot_label=True)
train_size = len(x_train)

print("データ読み込み完了")

# 重み初期値補正係数
wieght_init = 0.01
#入力層サイズ
input_layer_size = 784
#中間層サイズ
hidden_layer_1_size = 40
hidden_layer_2_size = 20

#出力層サイズ
output_layer_size = 10
# 繰り返し数
iters_num = 2000
# ミニバッチサイズ
batch_size = 100
# 学習率
learning_rate = 0.1
# 描写頻度
plot_interval=10

# 初期設定
def init_network():
    network = {} 

    ###########  変更箇所  ##############

    # Heの初期値
    network['W1'] = np.random.randn(input_layer_size, hidden_layer_1_size) / np.sqrt(input_layer_size) * np.sqrt(2)
    network['W2'] = np.random.randn(hidden_layer_1_size, hidden_layer_2_size) / np.sqrt(hidden_layer_1_size) * np.sqrt(2)
    network['W3'] = np.random.randn(hidden_layer_2_size, output_layer_size) / np.sqrt(hidden_layer_2_size) * np.sqrt(2)
        
    #################################
    
    network['b1'] = np.zeros(hidden_layer_1_size)
    network['b2'] = np.zeros(hidden_layer_2_size)
    network['b3'] = np.zeros(output_layer_size)

    return network

# 順伝播
def forward(network, x):
    W1, W2, W3 = network['W1'], network['W2'], network['W3']
    b1, b2, b3 = network['b1'], network['b2'], network['b3']

    ###########  変更箇所  ##############
    
    hidden_f = functions.relu
    
    #################################
    
    u1 =  np.dot(x, W1) + b1
    z1 = hidden_f(u1)
    u2 =  np.dot(z1, W2) + b2
    z2 = hidden_f(u2)
    u3 =  np.dot(z2, W3) + b3
    y = functions.softmax(u3)
 
    return z1, z2, y

# 誤差逆伝播
def backward(x, d, z1, z2, y):
    grad = {}
    
    W1, W2, W3 = network['W1'], network['W2'], network['W3']
    b1, b2, b3 = network['b1'], network['b2'], network['b3']
    
    ###########  変更箇所  ##############
    
    hidden_d_f = functions.d_relu
    
    #################################
    
    # 出力層でのデルタ
    delta3 = functions.d_softmax_with_loss(d, y)
    # b3の勾配
    grad['b3'] = np.sum(delta3, axis=0)
    # W3の勾配
    grad['W3'] = np.dot(z2.T, delta3)
    # 2層でのデルタ
    delta2 = np.dot(delta3, W3.T) * hidden_d_f(z2)
    # b2の勾配
    grad['b2'] = np.sum(delta2, axis=0)
    # W2の勾配
    grad['W2'] = np.dot(z1.T, delta2)
    # 1層でのデルタ
    delta1 = np.dot(delta2, W2.T) * hidden_d_f(z1)
    # b1の勾配
    grad['b1'] = np.sum(delta1, axis=0)
    # W1の勾配
    grad['W1'] = np.dot(x.T, delta1)

    return grad

# パラメータの初期化
network = init_network()

accuracies_train = []
accuracies_test = []

# 正答率
def accuracy(x, d):
    z1, z2, y = forward(network, x)
    y = np.argmax(y, axis=1)
    if d.ndim != 1 : d = np.argmax(d, axis=1)
    accuracy = np.sum(y == d) / float(x.shape[0])
    return accuracy

for i in range(iters_num):
    # ランダムにバッチを取得    
    batch_mask = np.random.choice(train_size, batch_size)
    # ミニバッチに対応する教師訓練画像データを取得    
    x_batch = x_train[batch_mask]
    # ミニバッチに対応する訓練正解ラベルデータを取得する
    d_batch = d_train[batch_mask]


    
    z1, z2, y = forward(network, x_batch)
    grad = backward(x_batch, d_batch, z1, z2, y)

    if (i+1)%plot_interval==0:
        accr_test = accuracy(x_test, d_test)
        accuracies_test.append(accr_test)
        
        accr_train = accuracy(x_batch, d_batch)
        accuracies_train.append(accr_train)

        print('Generation: ' + str(i+1) + '. 正答率(トレーニング) = ' + str(accr_train))
        print('                : ' + str(i+1) + '. 正答率(テスト) = ' + str(accr_test))
        
    # パラメータに勾配適用
    for key in ('W1', 'W2', 'W3', 'b1', 'b2', 'b3'):
        network[key]  -= learning_rate * grad[key]


lists = range(0, iters_num, plot_interval)
plt.plot(lists, accuracies_train, label="training set")
plt.plot(lists, accuracies_test,  label="test set")
plt.legend(loc="lower right")
plt.title("accuracy")
plt.xlabel("count")
plt.ylabel("accuracy")
plt.ylim(0, 1.0)
# グラフの表示
plt.show()
    

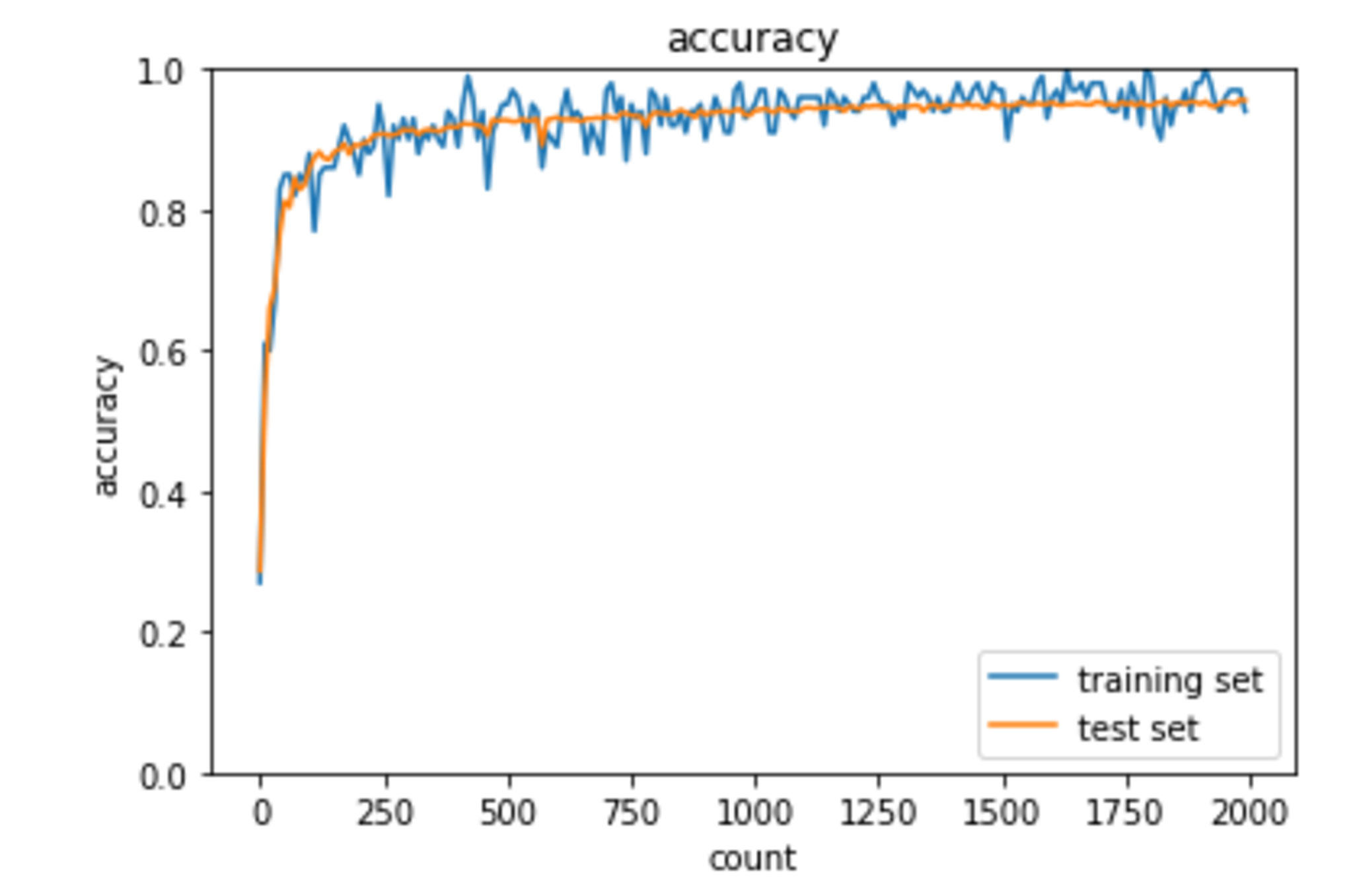
こちらも学習がうまく進んでいるように見受けられる。

バッチ正規化の実装例

      import numpy as np
from collections import OrderedDict
from common import layers
from data.mnist import load_mnist
import matplotlib.pyplot as plt
from multi_layer_net import MultiLayerNet
from common import optimizer

# バッチ正則化 layer
class BatchNormalization:
    '''
    gamma: スケール係数
    beta: オフセット
    momentum: 慣性
    running_mean: テスト時に使用する平均
    running_var: テスト時に使用する分散
    '''
    def __init__(self, gamma, beta, momentum=0.9, running_mean=None, running_var=None):
        self.gamma = gamma
        self.beta = beta
        self.momentum = momentum
        self.input_shape = None

        self.running_mean = running_mean
        self.running_var = running_var  
        
        # backward時に使用する中間データ
        self.batch_size = None
        self.xc = None
        self.std = None
        self.dgamma = None
        self.dbeta = None

    def forward(self, x, train_flg=True):
        if self.running_mean is None:
            N, D = x.shape
            self.running_mean = np.zeros(D)
            self.running_var = np.zeros(D)
                        
        if train_flg:
            mu = x.mean(axis=0) # 平均
            xc = x - mu # xをセンタリング
            var = np.mean(xc**2, axis=0) # 分散
            std = np.sqrt(var + 10e-7) # スケーリング
            xn = xc / std
            
            self.batch_size = x.shape[0]
            self.xc = xc
            self.xn = xn
            self.std = std
            self.running_mean = self.momentum * self.running_mean + (1-self.momentum) * mu # 平均値の加重平均
            self.running_var = self.momentum * self.running_var + (1-self.momentum) * var #分散値の加重平均
        else:
            xc = x - self.running_mean
            xn = xc / ((np.sqrt(self.running_var + 10e-7)))
            
        out = self.gamma * xn + self.beta 
        
        return out

    def backward(self, dout):
        dbeta = dout.sum(axis=0)
        dgamma = np.sum(self.xn * dout, axis=0)
        dxn = self.gamma * dout
        dxc = dxn / self.std
        dstd = -np.sum((dxn * self.xc) / (self.std * self.std), axis=0)
        dvar = 0.5 * dstd / self.std
        dxc += (2.0 / self.batch_size) * self.xc * dvar
        dmu = np.sum(dxc, axis=0)
        dx = dxc - dmu / self.batch_size
        
        self.dgamma = dgamma
        self.dbeta = dbeta

        return dx    

# 処理の開始 ==================================
(x_train, d_train), (x_test, d_test) = load_mnist(normalize=True)

print("データ読み込み完了")


# batch_normalizationの設定 =======================
use_batchnorm = True
# use_batchnorm = False
# ====================================================

network = MultiLayerNet(input_size=784, hidden_size_list=[40, 20], output_size=10,
                        activation='sigmoid', weight_init_std='Xavier', use_batchnorm=use_batchnorm)

iters_num = 1000
train_size = x_train.shape[0]
batch_size = 100
learning_rate=0.01

train_loss_list = []
accuracies_train = []
accuracies_test = []

plot_interval=10


for i in range(iters_num):
    batch_mask = np.random.choice(train_size, batch_size)
    x_batch = x_train[batch_mask]
    d_batch = d_train[batch_mask]

    grad = network.gradient(x_batch, d_batch)
    for key in ('W1', 'W2', 'W3', 'b1', 'b2', 'b3'):
        network.params[key] -= learning_rate * grad[key]

        loss = network.loss(x_batch, d_batch)
        train_loss_list.append(loss)        
        
    if (i + 1) % plot_interval == 0:
        accr_test = network.accuracy(x_test, d_test)
        accuracies_test.append(accr_test)        
        accr_train = network.accuracy(x_batch, d_batch)
        accuracies_train.append(accr_train)
        
        print('Generation: ' + str(i+1) + '. 正答率(トレーニング) = ' + str(accr_train))
        print('                : ' + str(i+1) + '. 正答率(テスト) = ' + str(accr_test))
                

lists = range(0, iters_num, plot_interval)
plt.plot(lists, accuracies_train, label="training set")
plt.plot(lists, accuracies_test,  label="test set")
plt.legend(loc="lower right")
plt.title("accuracy")
plt.xlabel("count")
plt.ylabel("accuracy")
plt.ylim(0, 1.0)
# グラフの表示
plt.show()
    

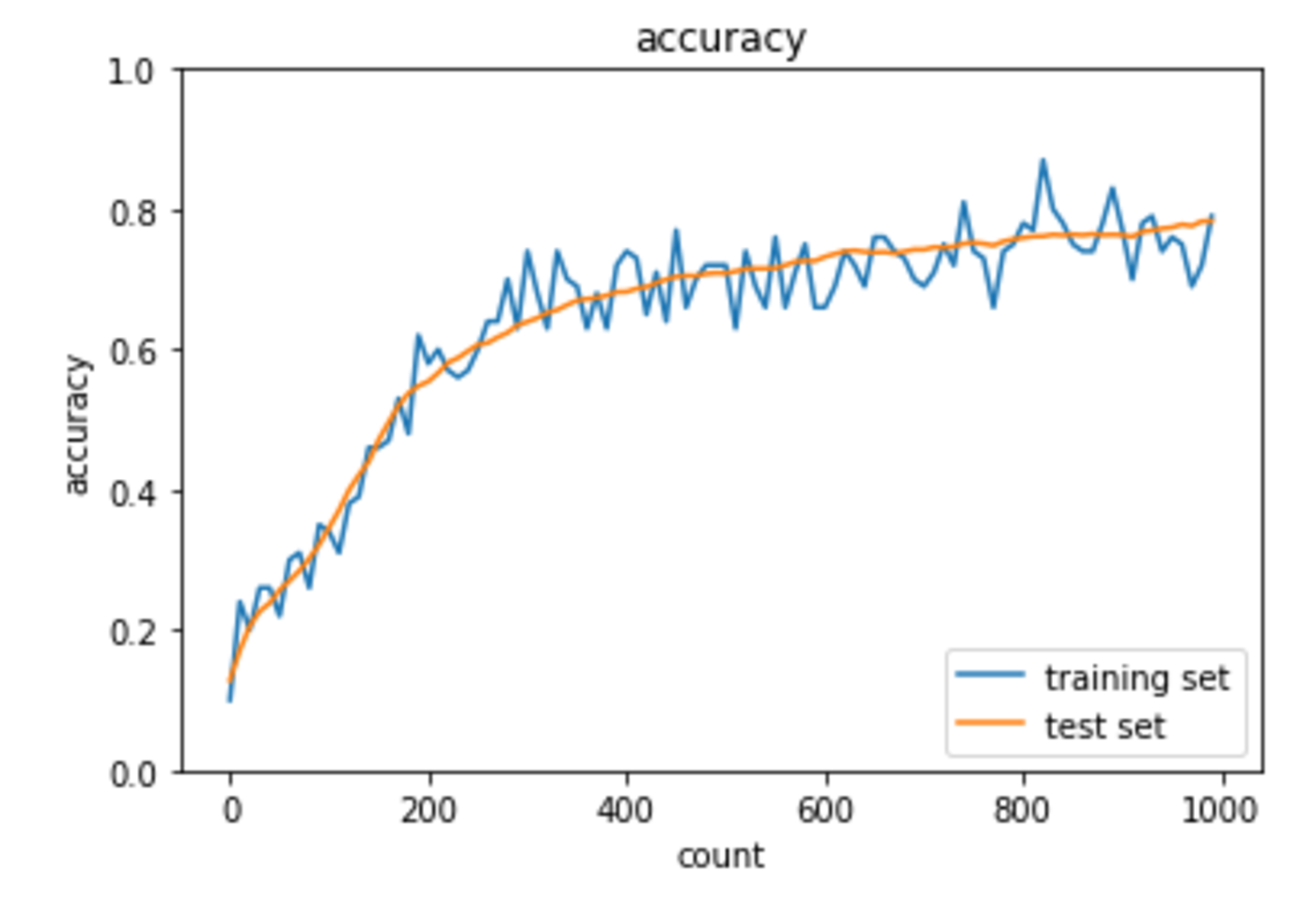
こちらも学習がうまく進んでいるように見受けられる。

Section2：学習率最適化手法

勾配降下法は、誤差をパラメータで微分したものと学習率の積を減算するものであった。それに対し、様々な工夫をすることで、問題点の解消や処理速度の改善等がなされている。

モメンタム

モメンタムは、誤差をパラメータで微分したものと学習率の積を減算した後、現在の重みに前回の重みを減算した値と慣性$\mu$の積を加算する。
\begin{align} V_{t} = \mu V_{t-1} - \epsilon \nabla E \\ w^{(t+1)} = w^{(t)} + V_{t} \end{align}

メリットは、以下の通り。

• 局所的最適解にはならず、大域的最適解となる。
• 谷間についてから最適解(最低値)に行くまでの時間が早い。

AdaGrad

AdaGradは、誤差をパラメータで微分したものと再定義した学習率の積を減算する。
\begin{align} h_{0} &= \theta \\ h_{t} &= h_{t-1} + (\nabla E)^2 \\ w^{(t+1)} &= w^{(t)} - \epsilon \frac{1}{\sqrt{h_{t}} + \theta} \nabla E \end{align}

メリットおよび課題は、以下の通り。

• メリット
  • 勾配の緩やかな斜面に対して、最適値に近づける。
• 課題
  • 学習率が徐々に小さくなるため、鞍点問題を引き起こす事がある。

RMSProp

誤差をパラメータで微分したものと再定義した学習率の積を減算する。
AdaGradとは再定義した値が違う。
\begin{align} h_{0} &= \theta \\ h_{t} &= \alpha h_{t-1} + (1 - \alpha) (\nabla E)^2 \\ w^{(t+1)} &= w^{(t)} - \epsilon \frac{1}{\sqrt{h_{t}} + \theta} \nabla E \end{align}

メリットとしては、以下の通り。

• 局所的最適解にはならず、大域的最適解となる。
• ハイパーパラメータの調整が必要な場合が少ない。

Adam

Adamとは以下を共に含んだ最適化アルゴリズムのこと。

• モメンタムの、過去の勾配の指数関数的減衰平均
• RMSPropの、過去の勾配の2乗の指数関数的減衰平均

メリットは、以下の通り。

• モメンタムおよびRMSPropのメリットを両立することができる。

まとめ

確認テストついでに、まとめを行う。

■確認テスト
モメンタム・AdaGrad・RMSPropの特徴をそれぞれ簡潔に説明せよ。

〇解答

• モメンタム
  • 局所的最適解にはならず、大域的最適解となる。
  • 谷間についてから最適解(最低値)に行くまでの時間が早い。
• AdaGrad
  • 勾配の緩やかな斜面に対して、最適値に近づける。
  • 学習率が徐々に小さくなるため、鞍点問題を引き起こす事がある。
• RMSProp
  • 局所的最適解にはならず、大域的最適解となる。
  • ハイパーパラメータの調整が必要な場合が少ない。

実装演習

ひと通り試してみた結果、いずれも学習が進んだ。特にRMSpropが一番早かった。

モメンタム

      # データの読み込み
(x_train, d_train), (x_test, d_test) = load_mnist(normalize=True, one_hot_label=True)

print("データ読み込み完了")

# batch_normalizationの設定 =======================
# use_batchnorm = True
use_batchnorm = False
# ====================================================

network = MultiLayerNet(input_size=784, hidden_size_list=[40, 20], output_size=10, activation='sigmoid', weight_init_std=0.01,
                       use_batchnorm=use_batchnorm)

iters_num = 1000
train_size = x_train.shape[0]
batch_size = 100
learning_rate = 0.3
# 慣性
momentum = 0.9

train_loss_list = []
accuracies_train = []
accuracies_test = []

plot_interval=10

for i in range(iters_num):
    batch_mask = np.random.choice(train_size, batch_size)
    x_batch = x_train[batch_mask]
    d_batch = d_train[batch_mask]

    # 勾配
    grad = network.gradient(x_batch, d_batch)
    if i == 0:
        v = {}
    for key in ('W1', 'W2', 'W3', 'b1', 'b2', 'b3'):
        if i == 0:
            v[key] = np.zeros_like(network.params[key])
        v[key] = momentum * v[key] - learning_rate * grad[key]
        network.params[key] += v[key]

        loss = network.loss(x_batch, d_batch)
        train_loss_list.append(loss)
        
    if (i + 1) % plot_interval == 0:
        accr_test = network.accuracy(x_test, d_test)
        accuracies_test.append(accr_test)        
        accr_train = network.accuracy(x_batch, d_batch)
        accuracies_train.append(accr_train)

        print('Generation: ' + str(i+1) + '. 正答率(トレーニング) = ' + str(accr_train))
        print('                : ' + str(i+1) + '. 正答率(テスト) = ' + str(accr_test))
        
        
lists = range(0, iters_num, plot_interval)
plt.plot(lists, accuracies_train, label="training set")
plt.plot(lists, accuracies_test,  label="test set")
plt.legend(loc="lower right")
plt.title("accuracy")
plt.xlabel("count")
plt.ylabel("accuracy")
plt.ylim(0, 1.0)
# グラフの表示
plt.show()
    

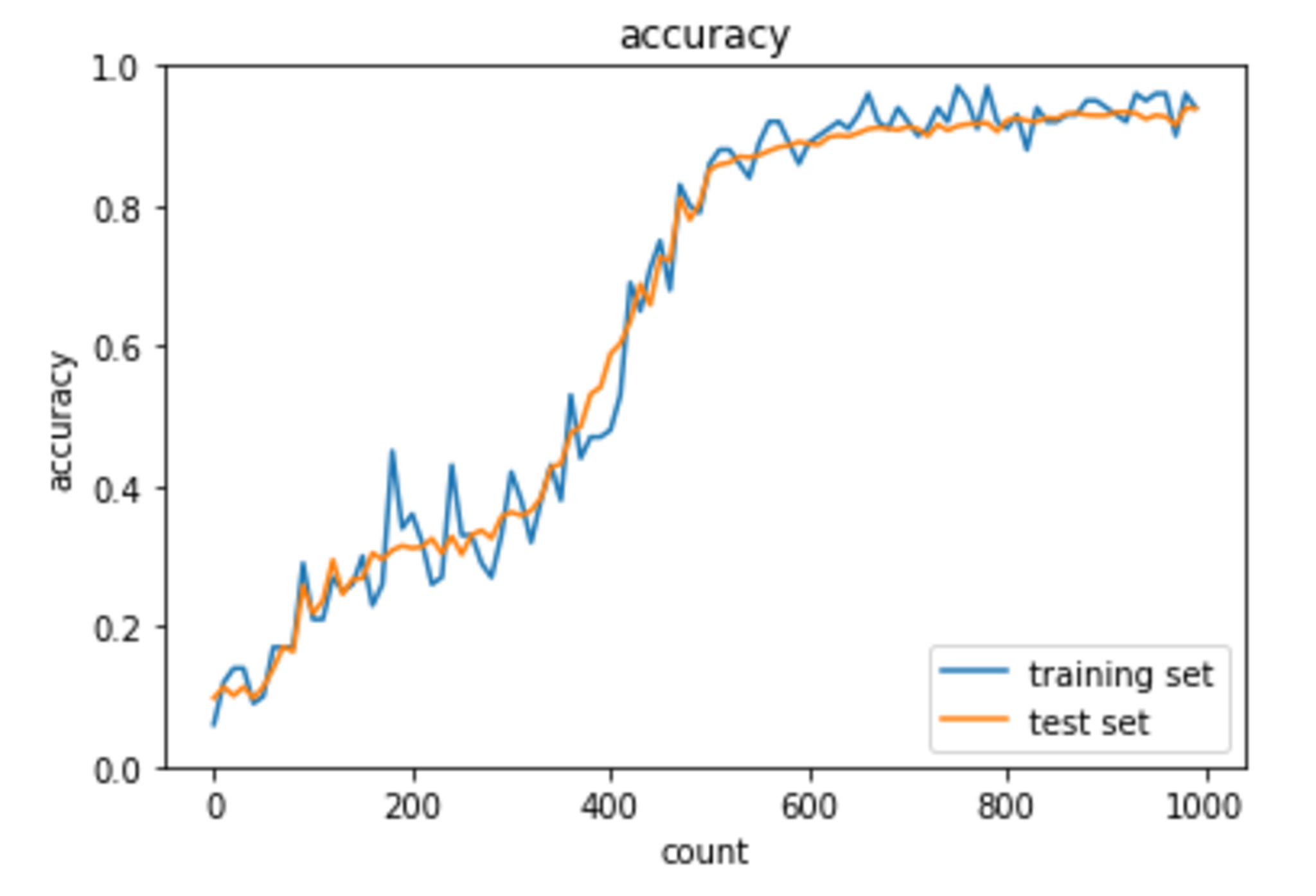
AdaGrad

$\theta$ = 1e-4 として計算した。

      # データの読み込み
(x_train, d_train), (x_test, d_test) = load_mnist(normalize=True, one_hot_label=True)

print("データ読み込み完了")

# batch_normalizationの設定 =======================
# use_batchnorm = True
use_batchnorm = False
# ====================================================

network = MultiLayerNet(input_size=784, hidden_size_list=[40, 20], output_size=10, activation='sigmoid', weight_init_std=0.01,
                       use_batchnorm=use_batchnorm)

iters_num = 1000
train_size = x_train.shape[0]
batch_size = 100
learning_rate = 0.1

train_loss_list = []
accuracies_train = []
accuracies_test = []

plot_interval=10

for i in range(iters_num):
    batch_mask = np.random.choice(train_size, batch_size)
    x_batch = x_train[batch_mask]
    d_batch = d_train[batch_mask]

    # 勾配
    grad = network.gradient(x_batch, d_batch)
    if i == 0:
        h = {}
    for key in ('W1', 'W2', 'W3', 'b1', 'b2', 'b3'):
        if i == 0:
            h[key] = np.full_like(network.params[key], 1e-4)
        else:
            h[key] += np.square(grad[key])
        network.params[key] -= learning_rate * grad[key] / (np.sqrt(h[key]))

        loss = network.loss(x_batch, d_batch)
        train_loss_list.append(loss)        
        
        
    if (i + 1) % plot_interval == 0:
        accr_test = network.accuracy(x_test, d_test)
        accuracies_test.append(accr_test)        
        accr_train = network.accuracy(x_batch, d_batch)
        accuracies_train.append(accr_train)
        
        print('Generation: ' + str(i+1) + '. 正答率(トレーニング) = ' + str(accr_train))
        print('                : ' + str(i+1) + '. 正答率(テスト) = ' + str(accr_test))
        
        
lists = range(0, iters_num, plot_interval)
plt.plot(lists, accuracies_train, label="training set")
plt.plot(lists, accuracies_test,  label="test set")
plt.legend(loc="lower right")
plt.title("accuracy")
plt.xlabel("count")
plt.ylabel("accuracy")
plt.ylim(0, 1.0)
# グラフの表示
plt.show()
    

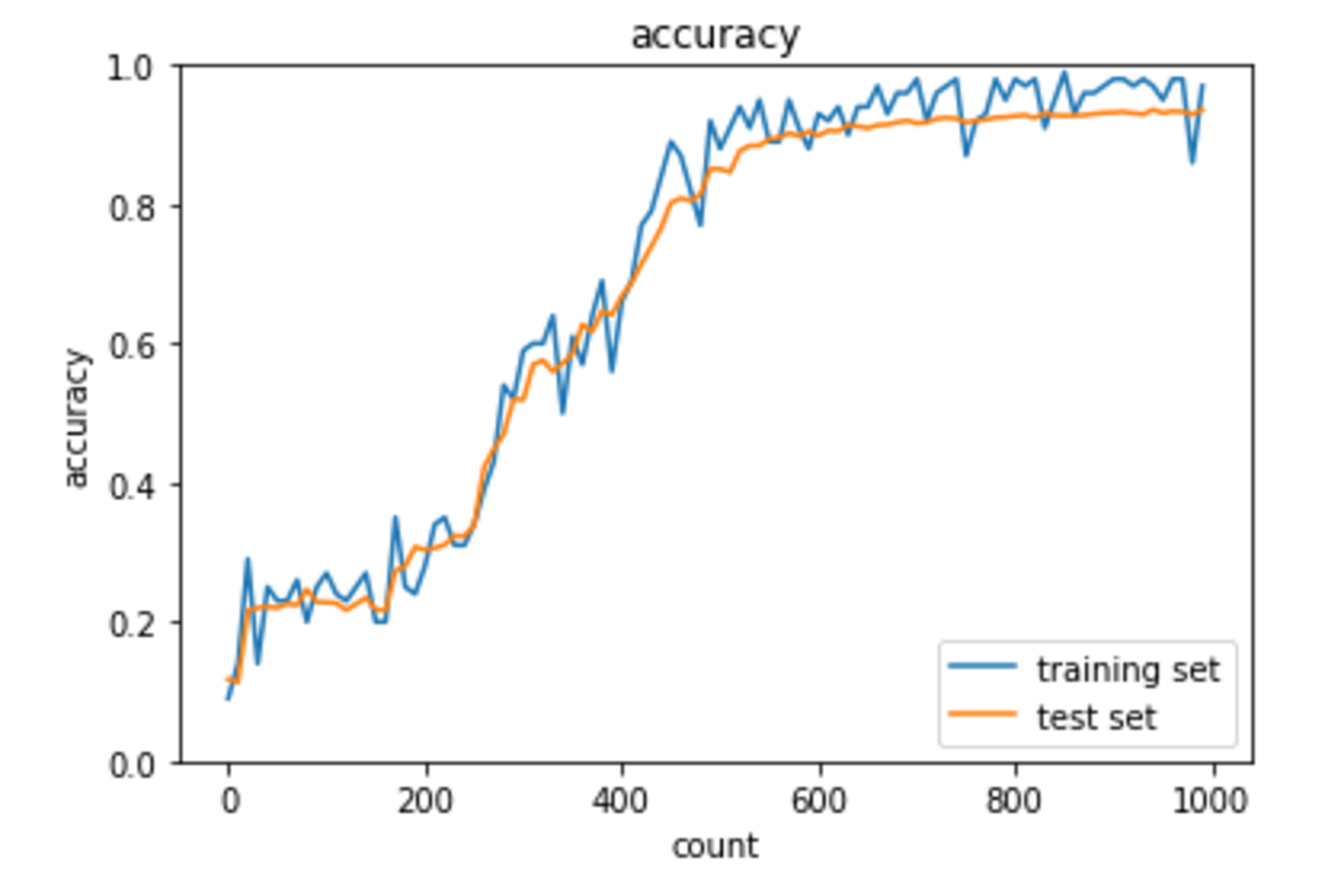
RMSprop

      # データの読み込み
(x_train, d_train), (x_test, d_test) = load_mnist(normalize=True, one_hot_label=True)

print("データ読み込み完了")

# batch_normalizationの設定 =======================
# use_batchnorm = True
use_batchnorm = False
# ====================================================

network = MultiLayerNet(input_size=784, hidden_size_list=[40, 20], output_size=10, activation='sigmoid', weight_init_std=0.01,
                       use_batchnorm=use_batchnorm)

iters_num = 1000
train_size = x_train.shape[0]
batch_size = 100
learning_rate = 0.01
decay_rate = 0.99

train_loss_list = []
accuracies_train = []
accuracies_test = []

plot_interval=10

for i in range(iters_num):
    batch_mask = np.random.choice(train_size, batch_size)
    x_batch = x_train[batch_mask]
    d_batch = d_train[batch_mask]

    # 勾配
    grad = network.gradient(x_batch, d_batch)
    if i == 0:
        h = {}
    for key in ('W1', 'W2', 'W3', 'b1', 'b2', 'b3'):
        if i == 0:
            h[key] = np.zeros_like(network.params[key])
        h[key] *= decay_rate
        h[key] += (1 - decay_rate) * np.square(grad[key])
        network.params[key] -= learning_rate * grad[key] / (np.sqrt(h[key]) + 1e-7)

        loss = network.loss(x_batch, d_batch)
        train_loss_list.append(loss)                
        
    if (i + 1) % plot_interval == 0:
        accr_test = network.accuracy(x_test, d_test)
        accuracies_test.append(accr_test)        
        accr_train = network.accuracy(x_batch, d_batch)
        accuracies_train.append(accr_train)
        
        print('Generation: ' + str(i+1) + '. 正答率(トレーニング) = ' + str(accr_train))
        print('                : ' + str(i+1) + '. 正答率(テスト) = ' + str(accr_test))
        
        
lists = range(0, iters_num, plot_interval)
plt.plot(lists, accuracies_train, label="training set")
plt.plot(lists, accuracies_test,  label="test set")
plt.legend(loc="lower right")
plt.title("accuracy")
plt.xlabel("count")
plt.ylabel("accuracy")
plt.ylim(0, 1.0)
# グラフの表示
plt.show()
    

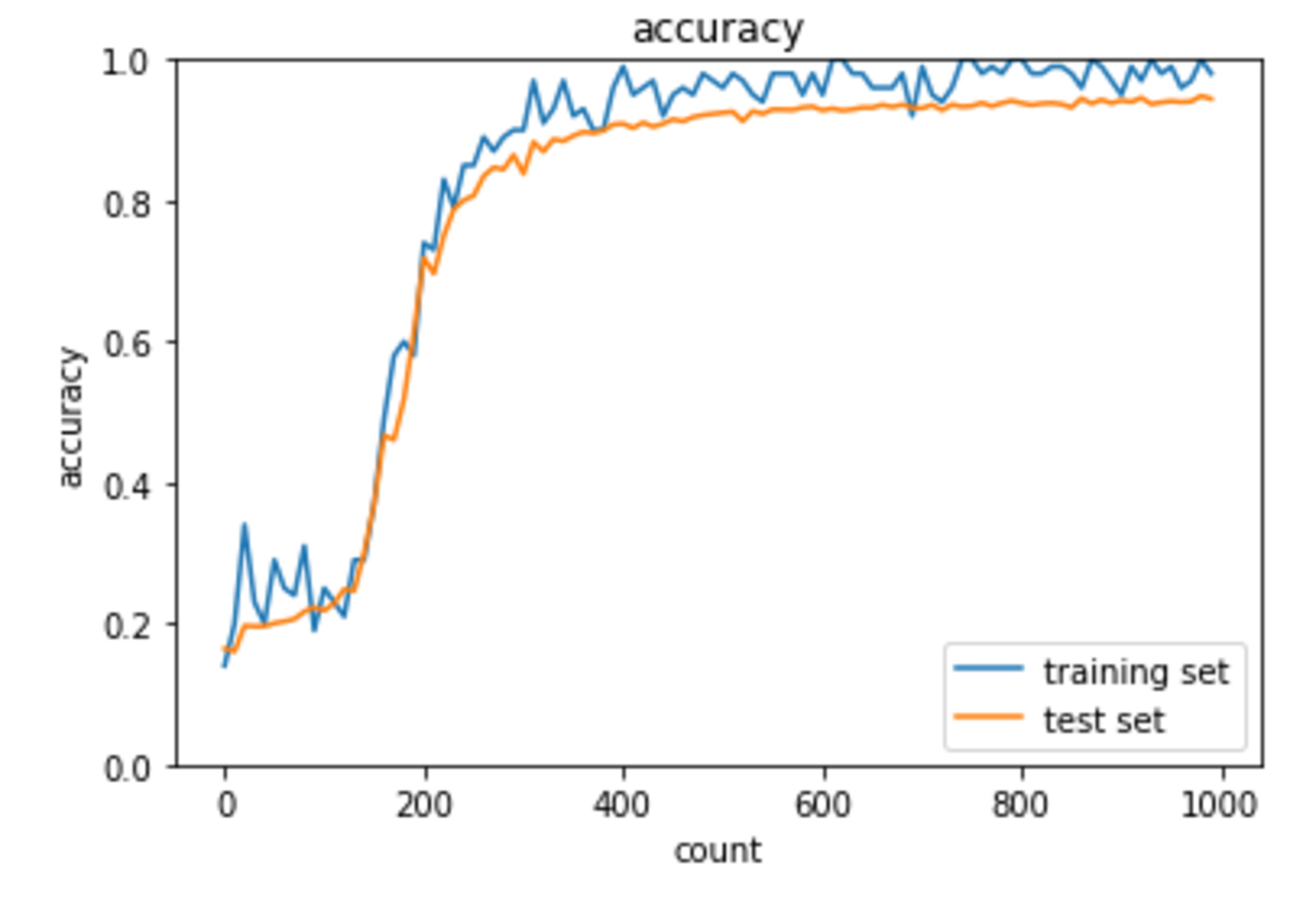
Adam

      # データの読み込み
(x_train, d_train), (x_test, d_test) = load_mnist(normalize=True, one_hot_label=True)

print("データ読み込み完了")

# batch_normalizationの設定 =======================
# use_batchnorm = True
use_batchnorm = False
# ====================================================

network = MultiLayerNet(input_size=784, hidden_size_list=[40, 20], output_size=10, activation='sigmoid', weight_init_std=0.01,
                       use_batchnorm=use_batchnorm)

iters_num = 1000
train_size = x_train.shape[0]
batch_size = 100
learning_rate = 0.01
beta1 = 0.9
beta2 = 0.999

train_loss_list = []
accuracies_train = []
accuracies_test = []

plot_interval=10

for i in range(iters_num):
    batch_mask = np.random.choice(train_size, batch_size)
    x_batch = x_train[batch_mask]
    d_batch = d_train[batch_mask]

    # 勾配
    grad = network.gradient(x_batch, d_batch)
    if i == 0:
        m = {}
        v = {}
    learning_rate_t  = learning_rate * np.sqrt(1.0 - beta2 ** (i + 1)) / (1.0 - beta1 ** (i + 1))    
    for key in ('W1', 'W2', 'W3', 'b1', 'b2', 'b3'):
        if i == 0:
            m[key] = np.zeros_like(network.params[key])
            v[key] = np.zeros_like(network.params[key])
            
        m[key] += (1 - beta1) * (grad[key] - m[key])
        v[key] += (1 - beta2) * (grad[key] ** 2 - v[key])            
        network.params[key] -= learning_rate_t * m[key] / (np.sqrt(v[key]) + 1e-7)                
        
        loss = network.loss(x_batch, d_batch)
        train_loss_list.append(loss)        
        
    if (i + 1) % plot_interval == 0:
        accr_test = network.accuracy(x_test, d_test)
        accuracies_test.append(accr_test)        
        accr_train = network.accuracy(x_batch, d_batch)
        accuracies_train.append(accr_train)
        
        print('Generation: ' + str(i+1) + '. 正答率(トレーニング) = ' + str(accr_train))
        print('                : ' + str(i+1) + '. 正答率(テスト) = ' + str(accr_test))
                

lists = range(0, iters_num, plot_interval)
plt.plot(lists, accuracies_train, label="training set")
plt.plot(lists, accuracies_test,  label="test set")
plt.legend(loc="lower right")
plt.title("accuracy")
plt.xlabel("count")
plt.ylabel("accuracy")
plt.ylim(0, 1.0)
# グラフの表示
plt.show()
    

Section3：過学習

過学習とは？

テスト誤差と訓練誤差とで学習曲線が乖離すること。(特定の訓練サンプルに対して、特化して学習する)

以下が原因で起こる。

• パラメータの数が多い
• パラメータの値が適切でない
• ノードが多い

ネットワークの自由度(層数、ノード数、パラメータの値etc...)が高い。

正則化

学習させていくと、重みにばらつきが発生するが、重みが大きい値をとることで、過学習が発生することがある。

過学習がおこりそうな重みの大きさ以下で重みをコントロールし、かつ重みの大きさにばらつきを出す必要があるため、誤差に対して、正則化項を加算することで、重みを抑制する。

具体的には、以下の式のように誤差に正則化項を加えることで重みの大きさを抑制する。
\begin{align} \tilde{E}_{n}(w) &= E_{n}(w) + \frac{1}{p} \lambda \|w\|_{p} \\ \|w\|_{p} &= (|w_1|^p + |w_2|^p + \cdots + |w_n|^p)^{1/p} \end{align}

ここで$p=1$のときをL1正則化(Lasso)、$p=2$のときをL2正則化(Ridge)という。

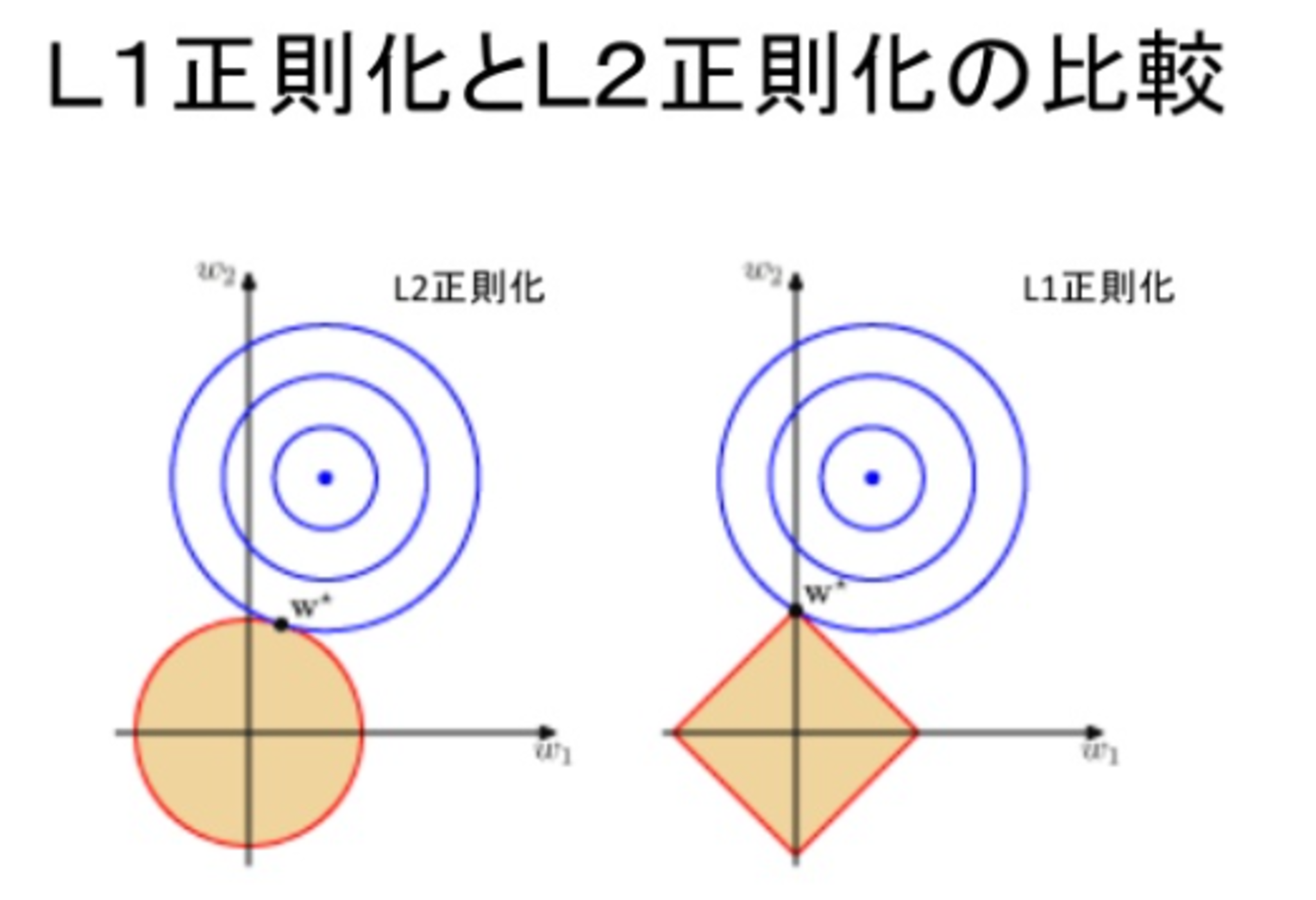正則化を表すグラフ
※上の図は https://www.slideshare.net/narumikanno0918/11wba-55283892 45ページより引用。

ドロップアウト

ノードの数が多い場合における過学習の対抗策。

ランダムにノードを削除して学習させる方法をドロップアウトという。データ量を変化させずに、異なるモデルを学習させていると解釈できる。

実装演習

過学習が起きている例

以下の例では過学習が起きていることを確認する。

      import numpy as np
from collections import OrderedDict
from common import layers
from data.mnist import load_mnist
import matplotlib.pyplot as plt
from multi_layer_net import MultiLayerNet
from common import optimizer


(x_train, d_train), (x_test, d_test) = load_mnist(normalize=True)

print("データ読み込み完了")

# 過学習を再現するために、学習データを削減
x_train = x_train[:300]
d_train = d_train[:300]

network = MultiLayerNet(input_size=784, hidden_size_list=[100, 100, 100, 100, 100, 100], output_size=10)
optimizer = optimizer.SGD(learning_rate=0.01)

iters_num = 1000
train_size = x_train.shape[0]
batch_size = 100

train_loss_list = []
accuracies_train = []
accuracies_test = []

plot_interval=10


for i in range(iters_num):
    batch_mask = np.random.choice(train_size, batch_size)
    x_batch = x_train[batch_mask]
    d_batch = d_train[batch_mask]

    grad = network.gradient(x_batch, d_batch)
    optimizer.update(network.params, grad)

    loss = network.loss(x_batch, d_batch)
    train_loss_list.append(loss)
        
    if (i+1) % plot_interval == 0:
        accr_train = network.accuracy(x_train, d_train)
        accr_test = network.accuracy(x_test, d_test)
        accuracies_train.append(accr_train)
        accuracies_test.append(accr_test)

        print('Generation: ' + str(i+1) + '. 正答率(トレーニング) = ' + str(accr_train))
        print('                : ' + str(i+1) + '. 正答率(テスト) = ' + str(accr_test))        

lists = range(0, iters_num, plot_interval)
plt.plot(lists, accuracies_train, label="training set")
plt.plot(lists, accuracies_test,  label="test set")
plt.legend(loc="lower right")
plt.title("accuracy")
plt.xlabel("count")
plt.ylabel("accuracy")
plt.ylim(0, 1.0)
# グラフの表示
plt.show()
    

これをベースにL2正則化、L1正則化、ドロップアウトについてみていく。

L2正則化

      from common import optimizer

(x_train, d_train), (x_test, d_test) = load_mnist(normalize=True)

print("データ読み込み完了")

# 過学習を再現するために、学習データを削減
x_train = x_train[:300]
d_train = d_train[:300]


network = MultiLayerNet(input_size=784, hidden_size_list=[100, 100, 100, 100, 100, 100], output_size=10)


iters_num = 1000
train_size = x_train.shape[0]
batch_size = 100
learning_rate=0.01

train_loss_list = []
accuracies_train = []
accuracies_test = []

plot_interval=10
hidden_layer_num = network.hidden_layer_num

# 正則化強度設定 ======================================
weight_decay_lambda = 0.1
# =================================================

for i in range(iters_num):
    batch_mask = np.random.choice(train_size, batch_size)
    x_batch = x_train[batch_mask]
    d_batch = d_train[batch_mask]

    grad = network.gradient(x_batch, d_batch)
    weight_decay = 0
    
    for idx in range(1, hidden_layer_num+1):
        grad['W' + str(idx)] = network.layers['Affine' + str(idx)].dW + weight_decay_lambda * network.params['W' + str(idx)]
        grad['b' + str(idx)] = network.layers['Affine' + str(idx)].db
        network.params['W' + str(idx)] -= learning_rate * grad['W' + str(idx)]
        network.params['b' + str(idx)] -= learning_rate * grad['b' + str(idx)]        
        weight_decay += 0.5 * weight_decay_lambda * np.sqrt(np.sum(network.params['W' + str(idx)] ** 2))

    loss = network.loss(x_batch, d_batch) + weight_decay
    train_loss_list.append(loss)        
        
    if (i+1) % plot_interval == 0:
        accr_train = network.accuracy(x_train, d_train)
        accr_test = network.accuracy(x_test, d_test)
        accuracies_train.append(accr_train)
        accuracies_test.append(accr_test)
        
        print('Generation: ' + str(i+1) + '. 正答率(トレーニング) = ' + str(accr_train))
        print('                : ' + str(i+1) + '. 正答率(テスト) = ' + str(accr_test))               


lists = range(0, iters_num, plot_interval)
plt.plot(lists, accuracies_train, label="training set")
plt.plot(lists, accuracies_test,  label="test set")
plt.legend(loc="lower right")
plt.title("accuracy")
plt.xlabel("count")
plt.ylabel("accuracy")
plt.ylim(0, 1.0)
# グラフの表示
plt.show()
    

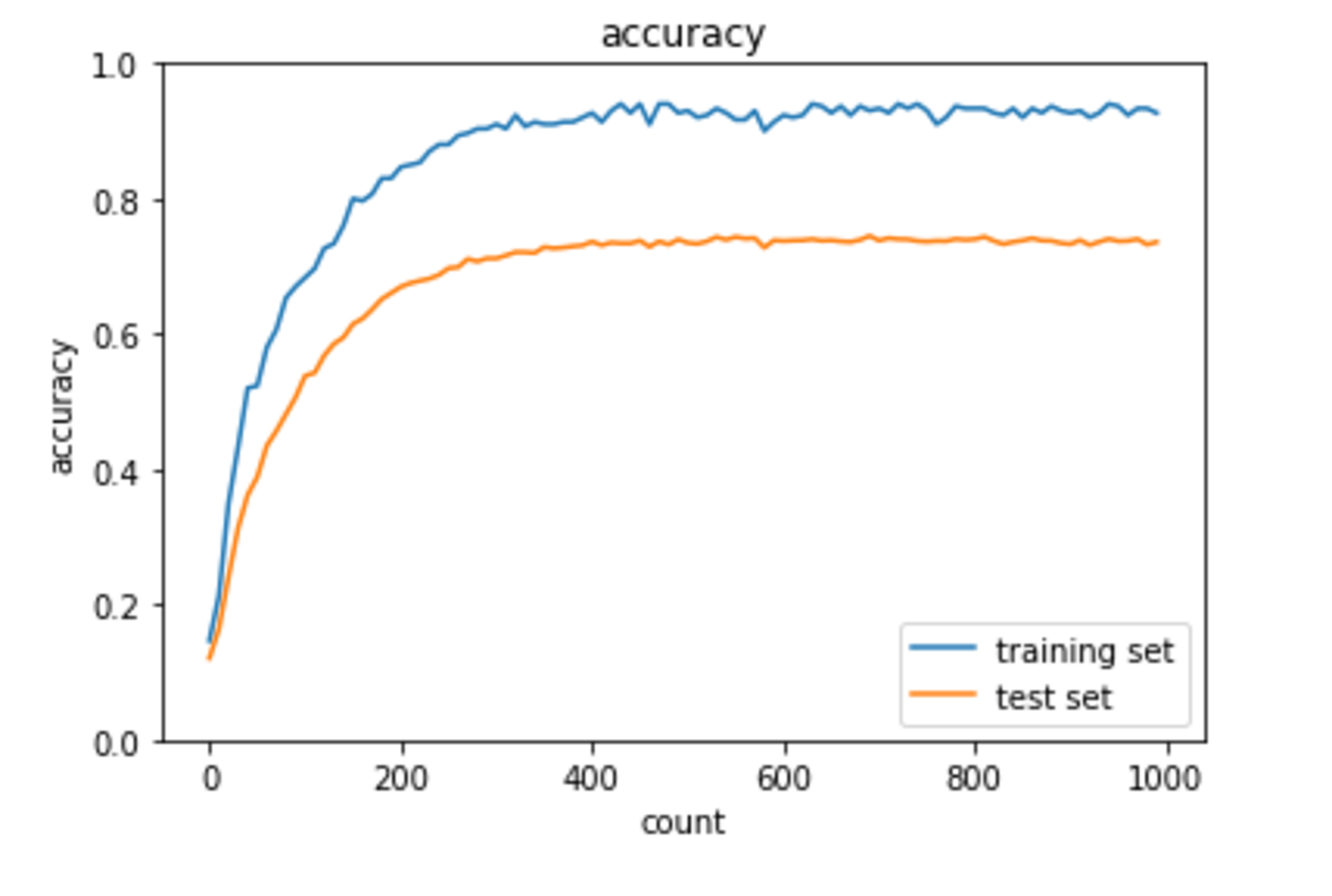
正則化項がない場合に比べて、訓練データの正解率とテストデータの正解率の乖離は小さくなっている。

L1正則化

      (x_train, d_train), (x_test, d_test) = load_mnist(normalize=True)

print("データ読み込み完了")

# 過学習を再現するために、学習データを削減
x_train = x_train[:300]
d_train = d_train[:300]

network = MultiLayerNet(input_size=784, hidden_size_list=[100, 100, 100, 100, 100, 100], output_size=10)


iters_num = 1000
train_size = x_train.shape[0]
batch_size = 100
learning_rate=0.1

train_loss_list = []
accuracies_train = []
accuracies_test = []

plot_interval=10
hidden_layer_num = network.hidden_layer_num

# 正則化強度設定 ======================================
weight_decay_lambda = 0.005
# =================================================

for i in range(iters_num):
    batch_mask = np.random.choice(train_size, batch_size)
    x_batch = x_train[batch_mask]
    d_batch = d_train[batch_mask]

    grad = network.gradient(x_batch, d_batch)
    weight_decay = 0
    
    for idx in range(1, hidden_layer_num+1):
        grad['W' + str(idx)] = network.layers['Affine' + str(idx)].dW + weight_decay_lambda * np.sign(network.params['W' + str(idx)])
        grad['b' + str(idx)] = network.layers['Affine' + str(idx)].db
        network.params['W' + str(idx)] -= learning_rate * grad['W' + str(idx)]
        network.params['b' + str(idx)] -= learning_rate * grad['b' + str(idx)]        
        weight_decay += weight_decay_lambda * np.sum(np.abs(network.params['W' + str(idx)]))

    loss = network.loss(x_batch, d_batch) + weight_decay
    train_loss_list.append(loss)        
        
    if (i+1) % plot_interval == 0:
        accr_train = network.accuracy(x_train, d_train)
        accr_test = network.accuracy(x_test, d_test)
        accuracies_train.append(accr_train)
        accuracies_test.append(accr_test)
        
        print('Generation: ' + str(i+1) + '. 正答率(トレーニング) = ' + str(accr_train))
        print('                : ' + str(i+1) + '. 正答率(テスト) = ' + str(accr_test))               
                
lists = range(0, iters_num, plot_interval)
plt.plot(lists, accuracies_train, label="training set")
plt.plot(lists, accuracies_test,  label="test set")
plt.legend(loc="lower right")
plt.title("accuracy")
plt.xlabel("count")
plt.ylabel("accuracy")
plt.ylim(0, 1.0)
# グラフの表示
plt.show()
    

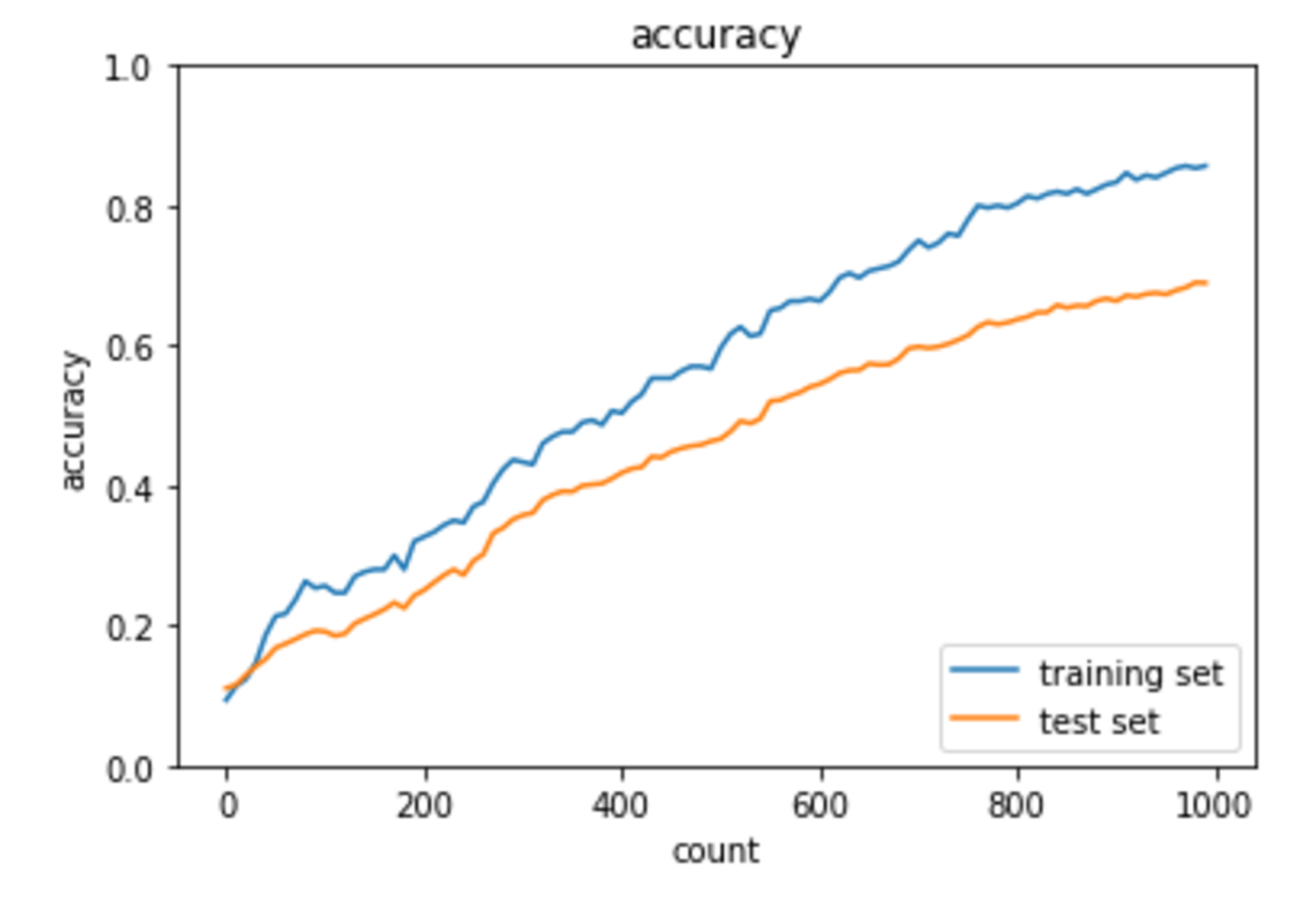
正則化項がない場合に比べて、過学習自体は発生していないように見受けられる。

ドロップアウト

      class Dropout:
    def __init__(self, dropout_ratio=0.5):
        self.dropout_ratio = dropout_ratio
        self.mask = None

    def forward(self, x, train_flg=True):
        if train_flg:
            self.mask = np.random.rand(*x.shape) > self.dropout_ratio
            return x * self.mask
        else:
            return x * (1.0 - self.dropout_ratio)

    def backward(self, dout):
        return dout * self.mask

from common import optimizer
(x_train, d_train), (x_test, d_test) = load_mnist(normalize=True)

print("データ読み込み完了")

# 過学習を再現するために、学習データを削減
x_train = x_train[:300]
d_train = d_train[:300]

# ドロップアウト設定 ======================================
use_dropout = True
dropout_ratio = 0.15
# ====================================================

network = MultiLayerNet(input_size=784, hidden_size_list=[100, 100, 100, 100, 100, 100], output_size=10,
                        weight_decay_lambda=weight_decay_lambda, use_dropout = use_dropout, dropout_ratio = dropout_ratio)
optimizer = optimizer.SGD(learning_rate=0.01)
# optimizer = optimizer.Momentum(learning_rate=0.01, momentum=0.9)
# optimizer = optimizer.AdaGrad(learning_rate=0.01)
# optimizer = optimizer.Adam()

iters_num = 1000
train_size = x_train.shape[0]
batch_size = 100

train_loss_list = []
accuracies_train = []
accuracies_test = []

plot_interval=10


for i in range(iters_num):
    batch_mask = np.random.choice(train_size, batch_size)
    x_batch = x_train[batch_mask]
    d_batch = d_train[batch_mask]

    grad = network.gradient(x_batch, d_batch)
    optimizer.update(network.params, grad)

    loss = network.loss(x_batch, d_batch)
    train_loss_list.append(loss)    
    
    if (i+1) % plot_interval == 0:
        accr_train = network.accuracy(x_train, d_train)
        accr_test = network.accuracy(x_test, d_test)
        accuracies_train.append(accr_train)
        accuracies_test.append(accr_test)

        print('Generation: ' + str(i+1) + '. 正答率(トレーニング) = ' + str(accr_train))
        print('                : ' + str(i+1) + '. 正答率(テスト) = ' + str(accr_test))        
        
lists = range(0, iters_num, plot_interval)
plt.plot(lists, accuracies_train, label="training set")
plt.plot(lists, accuracies_test,  label="test set")
plt.legend(loc="lower right")
plt.title("accuracy")
plt.xlabel("count")
plt.ylabel("accuracy")
plt.ylim(0, 1.0)
# グラフの表示
plt.show()
    

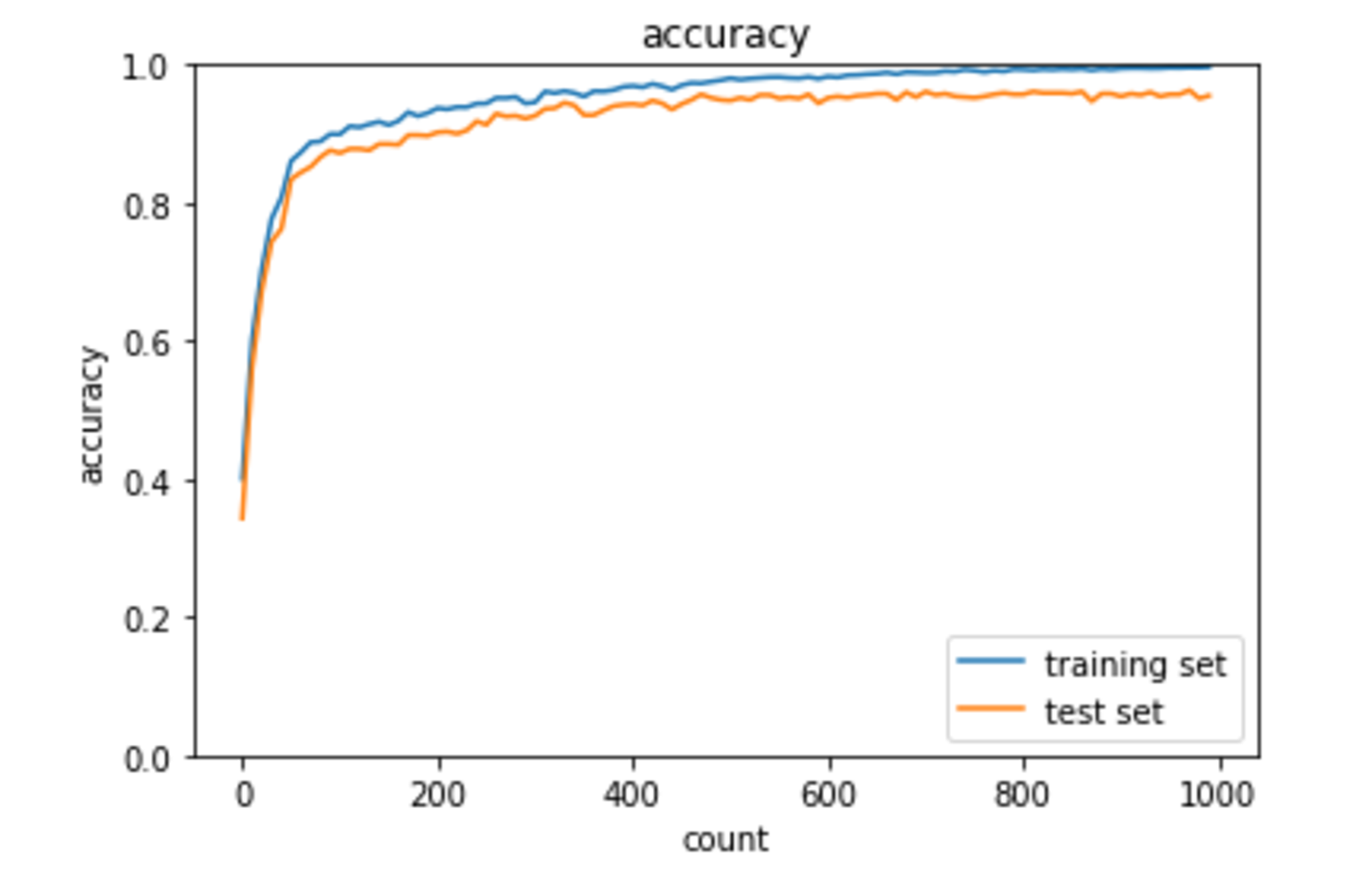
正則化項がない場合に比べて、緩やかに学習が進んでいるように見受けられる。

Section4：畳み込みニューラルネットワークの概念

畳み込みニューラルネットワーク(CNN)は、画像認識を中心に音声認識などあらゆる分野で用いられる。

複数の畳み込み層とプーリング層から構成されるという特徴がある。

畳み込み層

畳み込み層とは、画像の場合、縦、横、チャンネルの3次元のデータをそのまま学習し、次の層に伝えることができる層のこと。ゆえに、3次元の空間情報も学習できる。

画像とフィルタ(カーネル)の積の総和にバイアスを加えることで算出することで特徴を抽出する。

パディング

パディングとは、画像の周囲に固定のデータを埋め込むことである(主に0を用いる)。

ストライド

ストライドとは、畳み込みを行うにあたり、フィルタを適用する位置の間隔のことを指す。

チャンネル

チャンネルとは、空間的な奥行きのことを指す。

例えばカラー画像の場合はRGBの3チャンネルに分けて畳み込みを行う。

プーリング層

対象領域の中から1つの値を取得する層のこと。

畳み込んだ後に行うこと、それであると思われるという特徴を持った値のみを抽出できる。

最大値プーリング

対象領域の中から、最大値を得ることによるプーリング方法。

平均値プーリング

対象領域内の平均値を得ることによるプーリング方法。

■確認テスト
サイズ$6 \times 6$の入力画像を、サイズ$2 \times 2$のフィルタで畳み込んだ時の出力画像のサイズを答えよ。なお、ストライドとパディングは$1$とする

〇解答
入力サイズを$W \times H$、フィルタサイズを$F_W \times F_H$、パディングを$p$、ストライドを$s$とし、畳み込み層の出力サイズを$O_W \times O_H$とすると、$O_W$および$O_H$は以下の通りである。
\begin{align} O_W &= \frac{W+2p-F_W}{s} + 1 \\ O_H &= \frac{H+2p-F_H}{s} + 1 \end{align}

式に定義で与えられた式を代入する。
\begin{align} O_W &= \frac{6 + 2 \times 1 - 2}{1} + 1 = 7 \\ O_H &= \frac{6 + 2 \times 1 - 2}{1} + 1 = 7 \end{align}

よって、$7 \times 7$となる。

実装演習

畳み込み層とプーリング層を１つずつ持つ畳み込みニューラルネットワークを実装した例である。

      class Convolution:
    # W: フィルター, b: バイアス
    def __init__(self, W, b, stride=1, pad=0):
        self.W = W
        self.b = b
        self.stride = stride
        self.pad = pad
        
        # 中間データ（backward時に使用）
        self.x = None   
        self.col = None
        self.col_W = None
        
        # フィルター・バイアスパラメータの勾配
        self.dW = None
        self.db = None

    def forward(self, x):
        # FN: filter_number, C: channel, FH: filter_height, FW: filter_width
        FN, C, FH, FW = self.W.shape
        N, C, H, W = x.shape
        # 出力値のheight, width
        out_h = 1 + int((H + 2 * self.pad - FH) / self.stride)
        out_w = 1 + int((W + 2 * self.pad - FW) / self.stride)
        
        # xを行列に変換
        col = im2col(x, FH, FW, self.stride, self.pad)
        # フィルターをxに合わせた行列に変換
        col_W = self.W.reshape(FN, -1).T

        out = np.dot(col, col_W) + self.b
        # 計算のために変えた形式を戻す
        out = out.reshape(N, out_h, out_w, -1).transpose(0, 3, 1, 2)

        self.x = x
        self.col = col
        self.col_W = col_W

        return out

    def backward(self, dout):
        FN, C, FH, FW = self.W.shape
        dout = dout.transpose(0, 2, 3, 1).reshape(-1, FN)

        self.db = np.sum(dout, axis=0)
        self.dW = np.dot(self.col.T, dout)
        self.dW = self.dW.transpose(1, 0).reshape(FN, C, FH, FW)

        dcol = np.dot(dout, self.col_W.T)
        # dcolを画像データに変換
        dx = col2im(dcol, self.x.shape, FH, FW, self.stride, self.pad)

        return dx

class SimpleConvNet:
    # conv - relu - pool - affine - relu - affine - softmax
    def __init__(self, input_dim=(1, 28, 28), conv_param={'filter_num':30, 'filter_size':5, 'pad':0, 'stride':1},
                 hidden_size=100, output_size=10, weight_init_std=0.01):
        filter_num = conv_param['filter_num']        
        filter_size = conv_param['filter_size']
        filter_pad = conv_param['pad']
        filter_stride = conv_param['stride']
        input_size = input_dim[1]
        conv_output_size = (input_size - filter_size + 2 * filter_pad) / filter_stride + 1
        pool_output_size = int(filter_num * (conv_output_size / 2) * (conv_output_size / 2))

        # 重みの初期化
        self.params = {}
        self.params['W1'] = weight_init_std * np.random.randn(filter_num, input_dim[0], filter_size, filter_size)
        self.params['b1'] = np.zeros(filter_num)
        self.params['W2'] = weight_init_std * np.random.randn(pool_output_size, hidden_size)
        self.params['b2'] = np.zeros(hidden_size)
        self.params['W3'] = weight_init_std * np.random.randn(hidden_size, output_size)
        self.params['b3'] = np.zeros(output_size)

        # レイヤの生成
        self.layers = OrderedDict()
        self.layers['Conv1'] = layers.Convolution(self.params['W1'], self.params['b1'], conv_param['stride'], conv_param['pad'])
        self.layers['Relu1'] = layers.Relu()
        self.layers['Pool1'] = layers.Pooling(pool_h=2, pool_w=2, stride=2)
        self.layers['Affine1'] = layers.Affine(self.params['W2'], self.params['b2'])
        self.layers['Relu2'] = layers.Relu()
        self.layers['Affine2'] = layers.Affine(self.params['W3'], self.params['b3'])

        self.last_layer = layers.SoftmaxWithLoss()

    def predict(self, x):
        for key in self.layers.keys():
            x = self.layers[key].forward(x)
        return x
        
    def loss(self, x, d):
        y = self.predict(x)
        return self.last_layer.forward(y, d)

    def accuracy(self, x, d, batch_size=100):
        if d.ndim != 1 : d = np.argmax(d, axis=1)
        
        acc = 0.0
        
        for i in range(int(x.shape[0] / batch_size)):
            tx = x[i*batch_size:(i+1)*batch_size]
            td = d[i*batch_size:(i+1)*batch_size]
            y = self.predict(tx)
            y = np.argmax(y, axis=1)
            acc += np.sum(y == td) 
        
        return acc / x.shape[0]

    def gradient(self, x, d):
        # forward
        self.loss(x, d)
        
        # backward
        dout = 1
        dout = self.last_layer.backward(dout)
        layers = list(self.layers.values())
        
        layers.reverse()
        for layer in layers:
            dout = layer.backward(dout)

        # 設定
        grad = {}
        grad['W1'], grad['b1'] = self.layers['Conv1'].dW, self.layers['Conv1'].db
        grad['W2'], grad['b2'] = self.layers['Affine1'].dW, self.layers['Affine1'].db
        grad['W3'], grad['b3'] = self.layers['Affine2'].dW, self.layers['Affine2'].db

        return grad


########
import pickle
import numpy as np
from collections import OrderedDict
from common import layers
from common import optimizer
from data.mnist import load_mnist
import matplotlib.pyplot as plt
from common import optimizer

# データの読み込み
(x_train, d_train), (x_test, d_test) = load_mnist(flatten=False)

print("データ読み込み完了")

# 処理に時間のかかる場合はデータを削減 
x_train, d_train = x_train[:5000], d_train[:5000]
x_test, d_test = x_test[:1000], d_test[:1000]


network = SimpleConvNet(input_dim=(1,28,28), conv_param = {'filter_num': 30, 'filter_size': 5, 'pad': 0, 'stride': 1},
                        hidden_size=100, output_size=10, weight_init_std=0.01)

optimizer = optimizer.Adam()

iters_num = 1000
train_size = x_train.shape[0]
batch_size = 100

train_loss_list = []
accuracies_train = []
accuracies_test = []

plot_interval=10



for i in range(iters_num):
    batch_mask = np.random.choice(train_size, batch_size)
    x_batch = x_train[batch_mask]
    d_batch = d_train[batch_mask]
    
    grad = network.gradient(x_batch, d_batch)
    optimizer.update(network.params, grad)

    loss = network.loss(x_batch, d_batch)
    train_loss_list.append(loss)

    if (i+1) % plot_interval == 0:
        accr_train = network.accuracy(x_train, d_train)
        accr_test = network.accuracy(x_test, d_test)
        accuracies_train.append(accr_train)
        accuracies_test.append(accr_test)
        
        print('Generation: ' + str(i+1) + '. 正答率(トレーニング) = ' + str(accr_train))
        print('                : ' + str(i+1) + '. 正答率(テスト) = ' + str(accr_test))               

lists = range(0, iters_num, plot_interval)
plt.plot(lists, accuracies_train, label="training set")
plt.plot(lists, accuracies_test,  label="test set")
plt.legend(loc="lower right")
plt.title("accuracy")
plt.xlabel("count")
plt.ylabel("accuracy")
plt.ylim(0, 1.0)
# グラフの表示
plt.show()
    

Section5：最新のCNN(2021年現在では最新とは言えない初期のモデル)

AlexNet

2012年にILSVRC（ImageNet Large Scale Visual Recognition Challenge）で優勝したモデルで、以下の論文にて提出された。

• Alex Krizhevsky & Ilya Sutskever & Geoffrey E. Hinton, ImageNet Classification with Deep Convolutional Neural Networks
  URL： https://papers.nips.cc/paper/4824-imagenet-classification-with-deep-convolutional-neural-networks.pdf

概要図は上記論文のFigure2に記載あり。

3つの畳み込み層、2つのプーリング層および3つの全結合層から構成され、ドロップアウトを使用した過学習の抑制を行っている。

AlexNetは現在ではほとんど使われていないが、複数の畳み込み層とプーリング層の構成および、過学習の抑制機構の取り入れなどの考え方は現在の標準的なアーキテクチャとなっている。