コッホ曲線とくりこみ群

くりこみ群の説明として使うコッホ曲線

くりこみ群は物理学において最も重要な解析手法のひとつです。様々な教科書・テキストに解説がありますが、それらの多くはある程度物理を知らないと理解しにくいように思います。

「コッホ曲線」は、そのフラクタル次元が無理数であることで有名です。そしてこの次元を求めることにくりこみ群の考え方を使うことができます。コッホ曲線は物理を知らずとも理解でき、かつ非常にシンプルな系なので、くりこみ群のコンセプトを解説するのにちょうどよいように思います。他の文献にもこのような解説があるかと思いますが、「車輪の再生産」を厭わずに、コッホ曲線を使ってくりこみ群を説明したいと思います$^{(脚注1)}$。

後半は物理の話ですが、興味の無い方は「物理学におけるくりこみ群」の前まで読めば十分です。

コッホ曲線の次元: "ふつうの"求め方

コッホ曲線の次元の求め方はご存知かもしれませんが、self-containedにするためにこれを書いておきます。

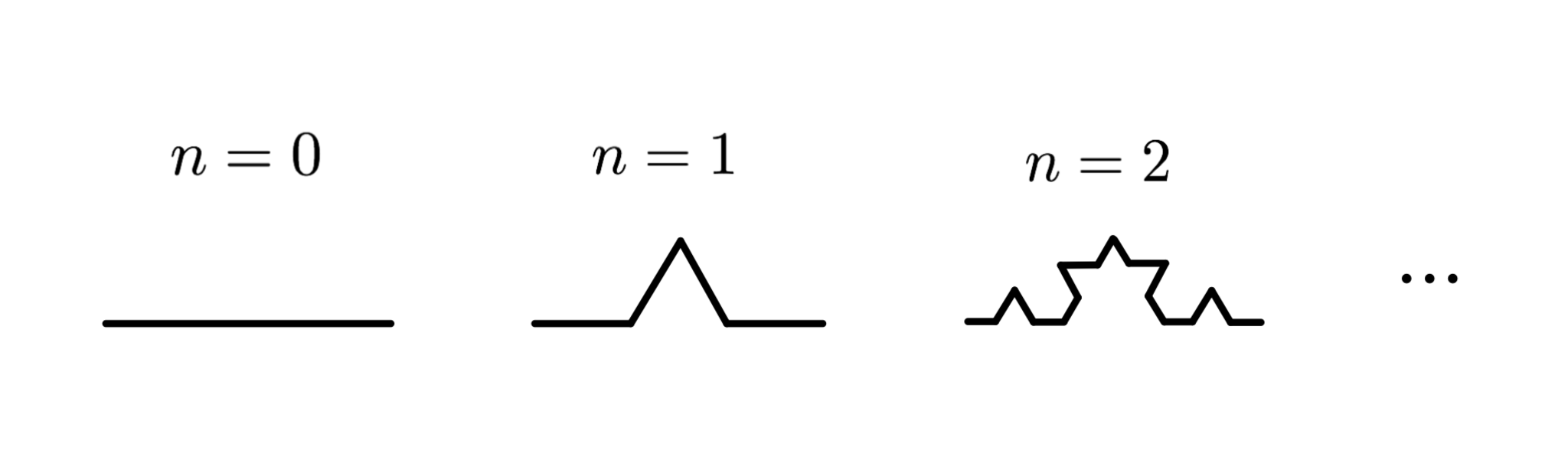コッホ曲線の構成法

コッホ曲線は図1のように構成します。最初に長さ$R$の直線がある状態を$n=0$次のコッホ曲線とします。次の次数では、この直線を3等分して、真ん中の線分を除き、さらに真ん中に底辺を除いた正三角形の折れ線を作ります。これを「$n=1$のコッホ曲線」とします。$n=0\to 1$の操作により、長さが4/3倍になります。$n$が増えるたび、この作業をすべてのちいさな線分に施します。これを$n$回繰り返したコッホ曲線を「$n$次のコッホ曲線」と呼びます。$n$を指定せずに「コッホ曲線」と呼んだ場合、$n\rightarrow \infty$の極限を指します。図2は$n=6$のコッホ曲線です。既に非常に複雑な構造を持つことがわかります。コッホ曲線の長さは一回の変換で長さが4/3倍になるため発散しています。

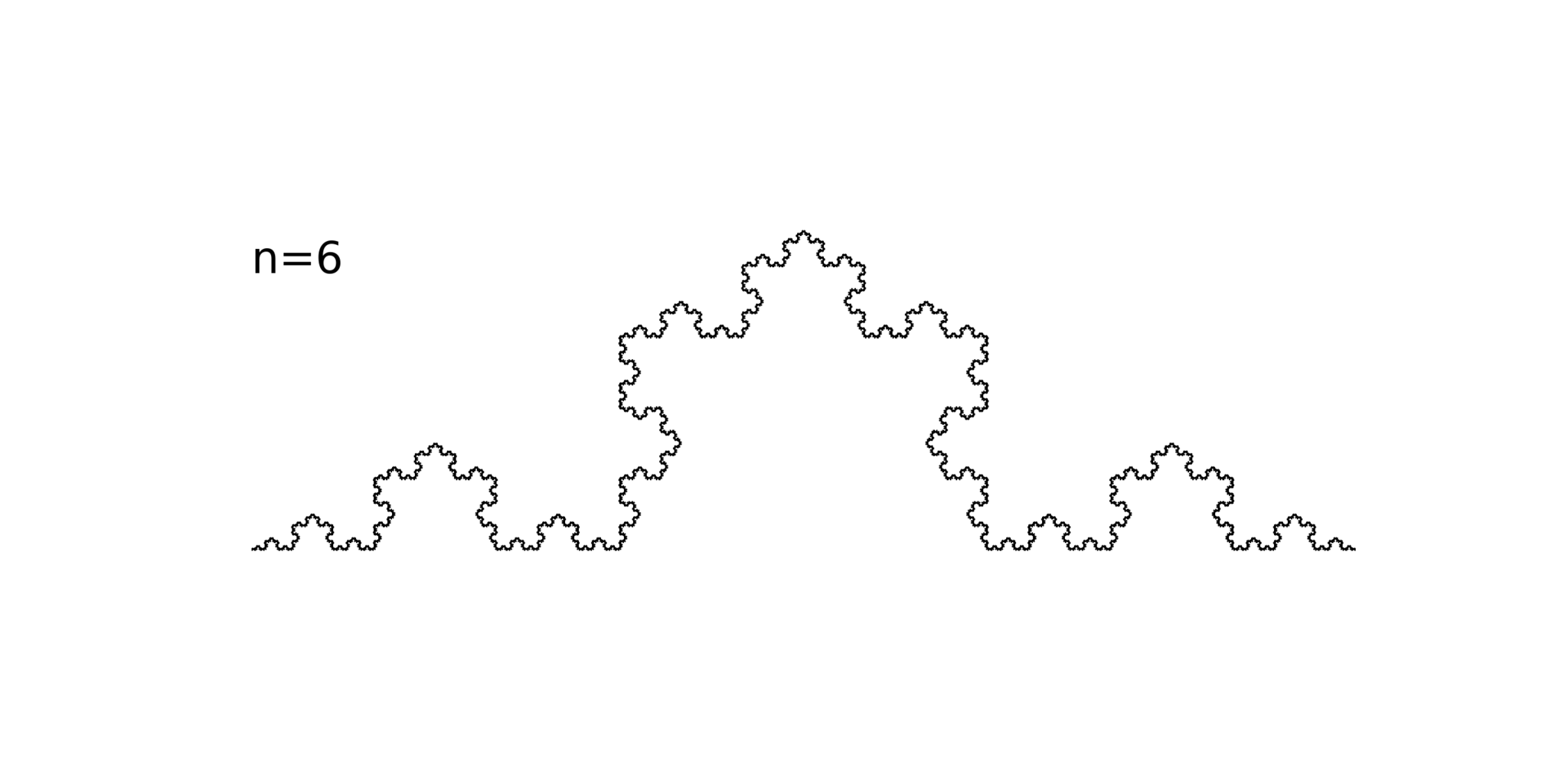n=6のコッホ曲線

コッホ曲線ではふつうの次元とはちがうフラクタル次元（〜ハウスドルフ次元）を定義することができます。この定義では、測る基準を変えたとき、その基準でオブジェクトの大きさがどう変化するかにより次元を定めます。いま$d$次元のオブジェクトが存在し、その一辺の長さが$R$だとします。大きさを測る基準を$r$とすると、オブジェクトの大きさは
\begin{align*} \left(\frac{R}{r}\right)^d \end{align*}
となります。この量を$\widehat L$とし（無次元量）、$r\rightarrow \lambda r$と$r$を変化させると
\begin{align*} \widehat L = \left(\frac{R}{r}\right)^d \rightarrow \left(\frac{R}{\lambda r}\right)^d=\lambda^{-d}\widehat L \end{align*}
と変化します。すなわち、$r\rightarrow\lambda r$と変換したときどれだけ$\widehat L$が変化するかがわかれば、次元$d$が求まります。

コッホ曲線の次元を求めます。その際重要なのが粗視化です。やることは単純で、基準$r$より短い構造を無視します。図3の左側のように$r=R/3$の基準で長さを測るときには、基準が最小単位の線分と同じ長さなので、山もちゃんと測ります。すると大きさは$R/3$の4こ分です。一方、右図のように基準を3倍して$r=R$で測るときには、山の構造より$r$が長いので、山を数えないことにします。すると図形の長さは$r$1つ分となります。このような粗視化の下で次元を求めると、上記の$\lambda$が$1/3$のとき$\widehat L$が4倍になるので
\begin{align*} 4&=\left(\frac{1}{3}\right)^{-d}\\ d&=\log4/\log3 \end{align*}
となります。よく知られているように、次元が無理数になります。

ここで行った測る基準の変更をスケール変換、これに対してある量がどれだけ変化するかをスケーリングと呼びます。

測る基準の変更に対するスケーリング。山の構造より長い基準を用いる場合、山を無視して粗視化する。

コッホ曲線の次元：くりこみ群的導出

今度はくりこみ群的考え方で次元$d$を求めます。やることはほぼ変わりませんが、思想が違います。

改めて以下の量を定義します：

一般には図形を特徴づける長さは複数あってもいいですが、ここでは1つしかない場合を考えます。このとき
\begin{align*} L(R,d,r)=R^d \end{align*}
となります。本来比例係数が存在しますが、ここでは1としました。1次元の線分・2次元の正方形・3次元の立方体の$L(R,d,r)$は、$R$をそれらの一辺の長さとすると、それぞれ$R^1, R^2, R^3$となるのでこれが成立しています。

$L$は実際の大きさであることから、測る基準$r$には依存しません。例えば$L$を「1次元、1mの物体の長さ」としたとき、これを$r$=1mという基準で測ろうとも1cmで測ろうとも1mmで測ろうとも、その表現が1m, 100cm, 1000mmと変わるだけで、大きさは変わりません。

これに対し$\widehat L(R,d,r)$を
\begin{align*} L(R,d,r)=r^d{\widehat L} (R,d,r) \end{align*}
で定義します。$L(R,d,r)=R^d$なので$\widehat L(R,d,r)=(R/r)^d$であり、これは図形の大きさを「$r$いくつ分」という単位で表した量です。$\widehat L$は無次元量なので、$R/r$の関数であることは重要です。

コッホ曲線では、前章で見たように粗視化によって
\begin{align*} \widehat L^{\rm CG}(R,d,r)\rightarrow \widehat L^{\rm CG}(R,d,\frac{r}{3})=4\widehat L^{\rm CG}(R,d,r) \end{align*}
となり、通常の次元1の図形とはスケーリングが変わります（図3参照）。ここでは$\widehat L$にCG(Coarse Graining, 粗視化)をつけて、粗視化されていることを強調しました。また細かいことですが、前章の$r$は「$\widehat L^{\rm CG}$の3つ目の引数」という意味で使っていたので、その具体的な値を$r=R$のように表していましたが、以下では$r$は基準の値そのものとします。

$L(R,d,r)=r^d \widehat L^{\rm CG}(R,d,r)$において$d=1$とすると、$L$が$r$に依存してしまいます。実際$r\rightarrow r/3$に対し
\begin{align*} L(R,d,r)\overset{r\rightarrow r/3}{\longrightarrow} L(R,d,\frac{r}{3})=\left(\frac{r}{3}\right)^1\widehat L^{\rm CG}(R,d,\frac{r}{3})=\frac{4r}{3}\widehat L^{\rm CG}(R,d,r)=\frac{4}{3} L(R,d,r) \end{align*}
となり変化します。

ここで粗視化をしても大きさ$L$は変化しないことを課します。つまり
\begin{align*} L(R,d,r)=L(R,d,\frac{r}{3}) \end{align*}
を課します。これを次元$d$を決定する方程式とみなし$d$を求めます。つまり、粗視化の影響を$d$におしつける（くりこむ）ことでこの式を成立させようというわけです。すると
\begin{align*} L(R,d,r)=r^d\widehat L^{\rm CG}(R,d,r) \overset{r\rightarrow r/3}{\longrightarrow} \frac{1}{3^d}r^d\widehat L^{\rm CG}(R,d,\frac{r}{3})=\frac{4}{3^d}L(R,d,r) \end{align*}
だから、$L$の不変性を課せば
\begin{align*} \frac{4}{3^d}=1 \ \ \ \therefore d=\log 4/\log 3 \end{align*}
となり、コッホ曲線のフラクタル次元が再現されます。

ここで行ったことをくりこみ群の言葉：「スケール変換」「くりこみ群方程式」と対応させると

となります。

あるパラメータがスケール変換に対して不変となる点を固定点(fixed point)と言います。この例の$d=\log4/\log3$はスケール変換に依存していないので、ある意味この値は固定点ですが、あまりに自明な例です。

コッホ曲線ではスケール変換は$r\rightarrow r/3$のみ考えればよかったですが、一般に$r\rightarrow r'$に対する「くりこみ群方程式」は
\begin{align*} L(R,d,r)=L(R,d,r') \end{align*}
となります。また、この変換が連続的な場合に微分方程式の形で書けば
\begin{align*} \frac{d}{dr}L(R,d,r)=0 \end{align*}
となります。

スケール依存するコッホ曲線

コッホ曲線の場合$d$を$r$に依存せずに定数にしておけば、粗視化の影響をすべて$d$にくりこむことができました。これはコッホ曲線がスケール不変性をもつからです。

しかし、一般にはくりこまれたパラメータはスケールに依存します。このような場合を考えるため、スケール依存するコッホ曲線として、こんな「変形コッホ曲線」$^{(注2)}$を考えてみます。

通常コッホ曲線を構成するとき、直線を3等分し真ん中に正3角形をつくるという作業をくりかえします（図4の左列参照）。
ここでこのルールを次のように変更します。$n$次の変換では、そのとき最小の直線を$n+2$等分します。その分割された直線を、それの1つぶんすきまを開けて2つ配置し、そのすきまを一辺とするような正(n+2)角形を作ります（図4の右列参照）。つまりはコッホ曲線の変換を$n$に応じて3角形、4角形、5角形...としたものです。ただしこれを行うと、図形全体の横幅が$3/(n+2)$倍に小さくなってしまうので、各段階ですべての線分を$(n+2)/3$倍することで、全体の横幅を一定に保ちます。$n$が大きいとき、通常のコッホ曲線と変形コッホ曲線は図5のようになります。

次数$n$=1から3のコッホ曲線（左列）および変形コッホ曲線（右列）

次数$n$=5と6のコッホ曲線（左列）および変形コッホ曲線（右列）

この図形はスケール依存した構造をもっているので、$d$は$r$に依存します。$d$を求めるため、変形コッホ曲線のスケーリングを粗視化して考えます。$n=0$での図形の横の長さを$R$として、$r$を$r=R\rightarrow R/3^n$と変換すると
\begin{align*} \widehat L^{\rm CG}(R,d,r=R)\rightarrow \hat L^{\rm CG}(R,d,r=R/3^n)= 4\cdot 5\cdot \cdots\cdot (n+3)\widehat L^{\rm CG}(R,d,r=R) \end{align*}
になることがわかります。よって"くりこみ群方程式"
\begin{align*} L(R,d,r=R)=L(R,d,r=R/3^n) \end{align*}
を要求すると
\begin{align*} R^d\widehat L^{\rm CG}(R,d,r=R)&=\frac{4\cdot 5\cdot \cdots\cdot (n+3)}{(3^n)^d}R^d \widehat L^{\rm CG}(R,d,r=R)\\ \therefore d&=\frac{\log 4+\log 5+\cdots +\log (n+3)}{n\log 3} \end{align*}
となります。つまり、測るスケールを$r=R/3$にしたら$d=\log4/\log3$、$r=R/9$にしたら$d=(\log4+\log5)/(2\log3)$という"くりこまれた"もしくは"有効的な"次元を使うと、コッホ曲線の長さ$L$は不変になり、粗視化に対して適切な計算を行うことができます。

無限大に煩わされない

ところで、コッホ曲線の$L$は本来発散しているのでした。しかしそんなこととは関係なく上の議論ができました。これは、$n$無限大のコッホ曲線に存在する無限に細かい構造を考えなくても、有限な$n$と$n+1$の間のスケール変換に対するスケーリングさえ考えれば上記の計算が可能だからです。

このようなくりこみ群の側面は、物理学、とくに場の量子論のような無限大の生じる場合でも同様です。

物理学におけるくりこみ群

以下、ここまでの話と物理学に出てくるくりこみ群との対応を考えます。ここでは特に素粒子物理学に出てくる場の量子論に対するくりこみ群方程式を紹介します。が、それをまじめにやると長くなるので、ここでは簡単に記述するだけにして、別の機会にもうすこしちゃんと書こうかと思います。

場の量子論

場の量子論とは、粒子を「場を量子化したもの」として扱い、それらの伝播・生成・消滅により現象を記述する理論です。量子力学では、例えば静止した電子が1つあればそれはずっと変わらず存在し、何も起きはしません。しかし、場の量子論では、電子からは光子が生成され、それがまた電子と反電子をうみ、...という過程が無数に起きていて、電子はこれを衣のようにまとっています。電子と電磁場を考える場合、量子電磁気学(Quantum ElectroDynamics, 以下QEDと呼びます)がこのような粒子生成（"真空の粒子生成"とよぶことにします）を記述する理論です。実際真空中の粒子生成の効果は観測できます。例えば電子の異常磁気モーメントと呼ばれる量（真空中の粒子生成による電子の"磁石性"の変化）は実験で非常に精密に測ることができるのですが、驚くことに、これは量子電磁気学による計算と8桁精度で一致しています。水素原子のエネルギー準位に対する真空中の粒子生成の効果も観測可能で、それには例えばLamb shiftと呼ばれるものがあります。Lamb shiftでは水素原子という複合体の計算が必要なので難しい要素がいくつかあるのですが、それでも水素原子のある2つのエネルギー準位の準位差はLamb shiftなしには説明できないことがわかっています。

ちなみに、量子場の理論は粒子しか扱えないからとても特殊な理論だと思うかもしれませんが、そうではありません。物質は究極的には全て粒子でできているので量子場の理論で記述できます。さらに、粒子間の力もゲージ粒子という粒子（QEDでは光子）により媒介されるので、これもまた量子場の理論で記述できます。よって、すべての物質粒子・ゲージ粒子を扱える量子場の理論があれば、それはすべてを説明できる究極の理論になります。

ただ、この量子場の理論、なにか物理量（電子の質量など）を計算しようとするとすぐに無限大が生じます。なぜかというと、たとえば電子の質量を計算する場合、電子から生まれる光子が無限に高いエネルギー・運動量を持てるからです。その効果を積分すると無限大になってしまいます。非常に大きなエネルギー・運動量をもつ粒子は、距離でいうと非常に小さいスケールに寄与します。場の量子論における電子のイメージは次のような感じです：「電子を顕微鏡で覗くと、粒子の生成・消滅が電子の周りに見える。それらのエネルギー・運動量は顕微鏡の拡大率を大きくすればするほど高くなり、それが無限に続く」。コッホ曲線も、ある一部を拡大すると、どんな部分にもさらに細かい構造が拡大前と同じように続いているのにある意味似ています。QEDの場合は拡大すればするほど複雑な構造を持ちます。

QEDなどの場の量子論では、くりこみ群の手法が非常に広く使われています。もともとくりこみ群は（たぶん）Gell-MannとLowが場の量子論に対して適用したのが最初ではないかと思います。いまではこの手法は様々な分野に応用されています。量子力学だけでなく、物性物理学・統計力学・古典力学・流体力学にも応用できます。おそらくは化学・生物学・情報科学・社会科学など、ほとんどすべての分野で応用があるのではないかと思います。数学では手法そのものが研究対象です。

場の量子論の具体的な計算は、基本的に複雑で面倒くさいです。どのようなダイアグラムを計算するかを選び、正則化の方法を決めてそれぞれのダイアグラムに対応する積分を計算し、くりこみ条件をおいて発散部分を除去し、有限部分を評価するという過程を経ます。初学者が計算すると、1つのダイアグラムの積分の評価だけで何時間もかかかったりします。計算の大変さ以前に、そもそも思想的に理解しがたい・納得いかないかもしれません。次元を複素化して4次元からちょっとだけずらすとか、無限大をパラメータにくりこむとか、なかなか馴染めないと思います。

以下場の量子論におけるくりこみ群を、このような面倒なこと・思想的に受け入れ難いことのない形で、コッホ曲線の場合と対応させて紹介します。

QCDにおける格子正則化によるくりこみ群

以下QEDではなくQCD(Quantum Chromedynamics、量子色力学)を考えます。

QCDは強い相互作用を記述する理論です。強い相互作用は原子核に働く、電磁気力より強い力です。QCDはQEDの拡張バージョンみたいなものです。電磁気学では電荷は1種類しかありませんが、QCDでは3種類あります。この3種類の電荷を色に例えて赤青緑と呼びます。これらをまとめて色電荷、または色荷と呼びます。QEDでは力を伝達する場として光子場（U(1)ゲージ場）が存在しますが、QCDではこれがグルーオンというものに置き換わります。またこの色電荷と結合する粒子としてクォークが存在します。電子のQCDバージョンだと思ってください。

なぜQEDでなくQCDを考えるかと言うと、クォークがなくても結合定数にくりこみが起こる系だからです。QEDでは電子の存在がくりこみに重要です。電子がなければ何も非自明なことは起こりません。それは光子が電荷をもたず、自己相互作用しないことによります。これに対してQCDでは、QEDの光子にあたるグルーオン自身が色電荷をもつため、クォークがなくても非自明なくりこみが起こります。クォークのないQCDはpure Yang-Millsと呼ばれます。

ここで重要なのは、pure Yang-Millsには次元をもつ量が存在しないことです。この理論にはグルーオンしか存在しないのですが、これは質量ゼロであるため、なにひとつ基準となる量が存在していません。このとき、スケーリングの議論が単純になります。

結局、ここでQCDを考える理由は、次元をもつパラメータがなく、かつ非自明なくりこみが起きる系だからです。

格子正則化

ここでは格子正則化におけるQCDを考えます。格子正則化では、くりこみ群方程式の構成が驚くほどシンプルでわかりやすくなります（ただし具体的な計算は逆に大変になることもありますが...）。以下、格子正則化におけるQCDのくりこみ・くりこみ群の考え方のエッセンスを紹介します。そしてこれは、上記したコッホ曲線と対応しています。

まず、必要な知識を提示します。

格子正則化における$a$は、コッホ曲線の$r$に対応しています。$g_0$はそれがのちにくりこまれるという意味でコッホ曲線の$d$に対応します（物理的な意味は違います）。場の量子論では無限大が出てくると言いましたが、格子正則化では$a\rightarrow 0$のときに無限大が生じます。逆に言えば有限の$a$では無限大は生じません。

さて、いまゴチャゴチャ計算することで、なんらかの物理量$H(R,g_0,a)$が計算できたとします。これは実際に実験で観測できる量だとします。それが何であるか・計算の詳細は一切関係なく、とにかく計算できたとします。ここで$R$とは、その物理量を特徴づける距離です。これは理論がもっているパラメータではなく、計算時に勝手に設定するものです。コッホ曲線で導入した$R$に対応するものだと思ってください。$H$として2つの静的な電荷の間に働くポテンシャルを考えることがあるのですが、この場合2つの電荷の距離が$R$に対応します。

ここで質問です：$a$はいくつでしょうか？

$a$は時空を格子に区切ったときの格子間隔でした。しかし、実際にはそんな格子など存在しません。世の中は連続的で、どんなに小さいところをみても、そんな格子など存在しません。計算上勝手に用意したものです。だから$a$がいくつかと聞かれても知らんがな！としか答えようがありません。ただ、$R$よりは十分短くないといけないでしょう。上に書いたように$a$より小さいスケールの物理は無視されてしまうので、$R$より$a$が大きければ、$R$くらいの距離の現象はすべて無視されてしまいます。一方で、$a$が$R$より十分小さければ、それを変化させても実際に観測される物理量$H$は変化しないでしょう。$a$というのは人工的に導入した量なのに、$H$がこれによりコロコロかわってしまったら困ります。
ということで、$H(R,g_0,a)$が$a$に依存しないことを要求しましょう：

\begin{align*} \ \ \ \ a\rightarrow a'\text{に対し}H(R,g_0,a)=H(R,g_0,a') \end{align*}

ところで、この$H$の$a$独立性はどのように実現されるのでしょうか。これはコッホ曲線の場合と同様、$g_0$が$a$に依存することで達成されます。すなわち、$a$より小さな寄与を無視した「しわ寄せ」を$g_0$におしつけようという考えです。このようにして、上の方程式の解$g_0$は$a$に依存します。これを$g_0(a)$と書くことにします。$g_0(a)$は$a$より小さなスケールの寄与がくりこまれた結合定数です。格子間隔$a$の格子上では、この$g_0(a)$を用いて計算を行えば、$a$に依存しない物理量$H(R,g_0(a),a)$が得られます。このようにして、人工的な量$a$に依存しない観測可能量が得られます。

QCDのくりこみ群方程式は、上記の「$H$の$a$非依存性」を微分方程式
\begin{align*} \frac{d}{da}H(R,g_0,a)=0 \end{align*}
で表します。そして$H$を$g_0$と$a$の関数と見て偏微分にして
\begin{align*} \frac{\partial}{\partial a}H(R,g_0,a)+\frac{\beta}{a}\frac{\partial}{\partial g_0}H(R,g_0,a)=0, \ \ \ \beta\equiv a\frac{\partial g_0}{\partial a} \end{align*}
と書き直します。$H(R,g_0,a)$を具体的に計算し（粗視化して計算する）、上の方程式に入れて$\beta$について解けば、$\beta(R,g_0,a)=f(R,g_0,a)$が求まります。さらに$\beta$の定義より、微分方程式
\begin{align*} a\frac{\partial g_0}{\partial a}=f(R,g_0,a) \end{align*}
を解けばスケール$a$に依存した$g_0$が求まります。

以上のように、スケール$a$より小さな現象を無視して物理量を計算するとき、元の$g_0$ではなく$g_0(a)$を用いると物理量は$a$に依存しなくなり、正しい結果を得られます。つまりは$g_0(a)$は$a$より小さい効果を含んだ「くりこまれた」または「有効的な」結合定数だとみなせます。これらは前章までのコッホ曲線の議論と対応しています。また、これもコッホ曲線のときと同様ですが、$a\rightarrow 0$で生じる無限大に煩わされずにくりこみ群方程式を構成し解くことができます。

上の議論における$\beta$は$\beta$関数と呼ばれ、これを計算することは場の量子論において大変重要です。

ここで述べたQCDにおける格子正則化でのくりこみに関しては、Refs[1,2]に詳しく書いてあります。興味のある方はご参照ください。

まとめ

とりあえずここまでにしておきます。今回は、コッホ曲線を通したくりこみ群の説明、およびコッホ曲線のくりこみと素粒子物理のくりこみとの対応、すなわち

を説明しました。具体的な$\beta$関数の計算、スケール不変性の量子力学的な破れ（次元転移、dimensional transmutation）などの話をそのうちしようかなと思います。

おしまい。

★本記事には続き: くりこみ群の応用：クォーク間ポテンシャルから「走る結合定数」を導く がありますので、宜しければ御覧ください。