Fibonacci 数の三乗和のもう一つの計算方法
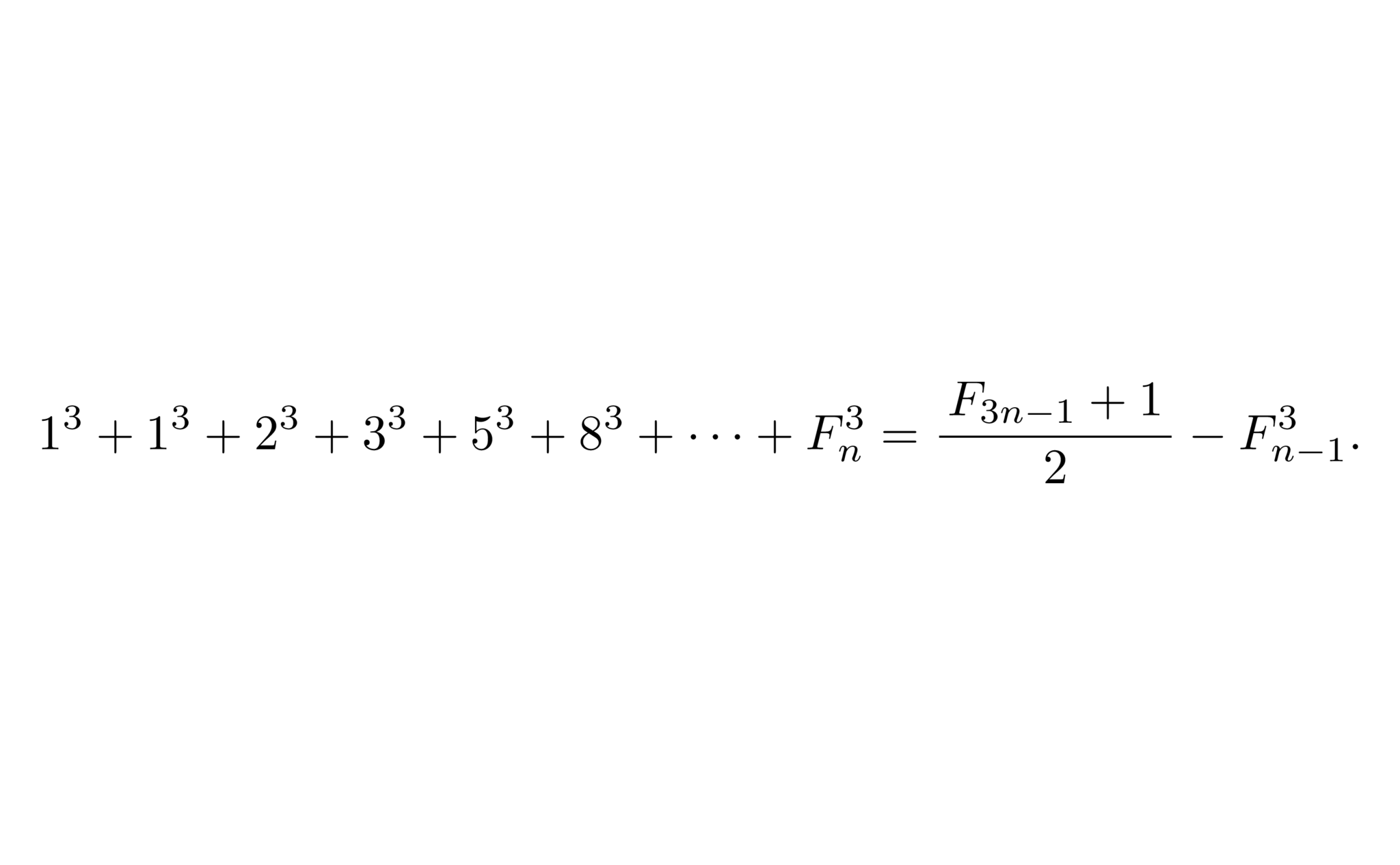三乗和の等式
前提知識 : Fibonacci 数 (漸化式による定義).
先日の記事.
https://mathlog.info/articles/2533
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
先日の記事において, Fibonacci 数の三乗和$\sum_1^nF_i^3$の簡易な計算手法を紹介しました. 今回は, これに引きつづき私の知っている証明をもう一通り共有しておこうと思います (既出であるかは判らない). 私の知る限りではこの方法による結果の式が最も短い形になります.
$F_{3n}=F_{n+1}^3+F_n^3-F_{n-1}^3. $
より一般の等式
\begin{align}
F_{l+m+n}=F_{l+1}F_{m+1}F_{n+1}+F_lF_mF_n-F_{l-1}F_{m-1}F_{n-1}
\end{align}
を証明すれば$l=m=n$を代入して命題の等式が得られるが, これは三重に帰納法を用いることによって$2^3$組の数字の代入で確かめられる (詳細略).
補足. 導出するには指数法則の等式$\phi^{l+m+n}=\phi^l\phi^m\phi^n$において両辺を$\mathbb{Z}[\phi]$の形式に表し比較して, 漸化式を用いて整理すれば可いです.
$\displaystyle\sum_{i=1}^{i=n}F_i=F_{n+2}-1.$
総和を偶数項目と奇数項目に分類し, 偶数項目の集まりに$-F_1+F_1$を, 奇数項目の集まりに$-F_0+F_0$を加えれば得られる. $\quad\Box$
$\displaystyle\sum_{i=1}^{i=n}F_{3i}=\frac{\,F_{3n+2}-1\,}{\,2\,}.$
漸化式により$4F_i=F_{i-2}+F_i+F_{i+2}$であることを用いれば
\begin{align}
4\sum_{i=1}^{i=n}F_{3i}&=\sum_{i=1}^{i=n}(F_{3i-2}+F_{3i}+F_{3i+2})\\
&=-F_2-F_{3n+1}+\sum_{j=1}^{j=3n+2}F_j\\
&=F_{3n+4}-F_{3n+1}-2=2F_{3n+2}-2
\end{align}
と計算することができる. $\quad\Box$
$\displaystyle\sum_{i=1}^{i=n}F_i^3=\frac{\,F_{3n-1}+1\,}{\,2\,}-F_{n-1}^3.$
等式$F_{i+1}^3+F_i^3-F_{i-1}^3=F_{3i}$の両辺を$1\leqslant i\leqslant n-1$の範囲で総和すれば
\begin{align}
-F_1^3+F_{n-1}^3+\sum_{i=1}^{i=n}F_i^3=\frac{\,F_{3n-1}-1\,}{\,2\,}
\end{align}
という等式になり, 直ちに命題の等式が導かれる. $\quad\Box$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
あるいは, 三項毎の漸化式として$F_{i+3}=4F_i+F_{i-3}$が成立することから
\begin{align}
0&=F_{3i+3}-4F_{3i}-F_{3i-3}\\
&=(F_{i+2}^3+F_{i+1}^3-F_i^3)-4(F_{i+1}^3+F_i^3-F_{i-1}^3)-(F_i^3+F_{i-1}^3-F_{i-2}^3)\\
&=F_{i+2}^3-3F_{i+1}^3-6F_i^3+3F_{i-1}^3+F_{i-2}^3
\end{align}
を導出しておき, これを総和することによっても別の形で三乗和が得られます. この方法は恐らくは既出ですが, いわゆる Fibonomial coefficients (フィボナッチ数列 bot ではエフ二項係数)を用いれば一般の$k$乗に拡張することができるという長所が有ります. 三乗和の計算法については他にも様々在りますので, 興味の有る方は是非挑戦してみてください.
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
